基于拉丁超立方体抽样的六自由度机械臂工作空间分析
杜健超,孙卫红,马冠宇
(中国计量学院 机电工程学院,杭州 310018)
基于拉丁超立方体抽样的六自由度机械臂工作空间分析
杜健超,孙卫红,马冠宇
(中国计量学院 机电工程学院,杭州310018)
摘要:针对六自由度机械臂史陶比尔RX-90的工作空间求解问题,提出一种基于拉丁超立方体抽样的统计计算方法。用D-H法对机械臂建立数学模型,采用连杆坐标系变换的方法求出其运动学正解。对比了蒙特卡罗法和拉丁超立方抽样(LHS)的优缺点,根据机械臂笛卡尔空间和关节空间的映射关系,设计LHS法分析其工作空间,在计算机输出设备显示工作空间的点云图并且得到各坐标轴取值范围。通过MATLAB机器人工具箱仿真验证了求解结果的正确性和有效性,为后续机械臂轨迹规划及优化、动力学分析、运动精度控制、系统优化等研究方向提供了参考依据。
关键词:六自由度机械臂;拉丁超立方体抽样;蒙特卡洛法
0引言
机械臂已广泛运用于工业生产[1],在机械臂的结构和性能研究中,有一个基本问题是分析其工作空间。工作空间的概念最早由B.Roth于1975年提出[2],概念为机械臂末端在各关节约束条件下能达到空间点的集合。工作空间反映了机械臂运动的灵活程度,是一个从几何角度阐述机械臂的性能的重要的运动学指标[3]。
传统的工作空间求解方法有图解法和解析法[4],图解法受限于关节数量,而解析法计算量大且不能保证所有边界曲面的可靠性。由于这些缺点,故近年来学者使用的较热门的方法为基于蒙特卡洛法的统计学计算求解法。何价来[5]等用蒙特卡洛法简单又形象地描绘了七自由度拟人机械臂的工作空间;陈泓伍[6]用蒙特卡洛法求解了水下清刷机械手的工作空间,为后续研究做好准备。然而蒙特卡洛法这种统计方法抽样的随机性很强,要得到较为精确的结果,需要选取大量的样本点,计算效率偏低。
本文在对比常用的两种统计抽样方法蒙特卡洛法和拉丁超立方体抽样(LHS)的计算效率后,采用更为高效的LHS分析史陶比尔RX-90机械臂的工作空间,在Matlab环境下得到其工作空间的点云图,并通过MATLAB机器人工具箱仿真验证。
1RX-90机械臂运动学分析
1.1D-H数学模型建立
史陶比尔RX-90机械臂属于关节式机器人,6个关节都是转动关节。我们对其建立如下图1所示的坐标体系。前3个关节确定手腕参考点的位置,后三个关节确定手腕的方位。


图1 RX-90坐标体系建立
如同大多数工业机器人[7],后3个关节轴线交于一点,该点选作为手腕的参考点,也是关节坐标系{4},{5}和{6}的原点。 关节1的轴线为铅直方向,关节2和3的轴线水平,且平行,距离为a2。关节1和2的轴线垂直相交,关节3和关节4的轴线垂直交错,距离为a3。相应的连杆参数如表1所示。
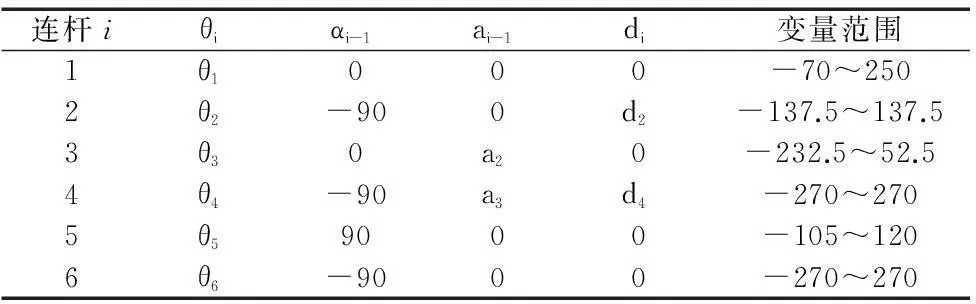
表1 RX-90机械臂D-H参数
其中a2=460,a3=195,d2=210,d4=450。
1.2机械臂运动学正解
运动学正解是指根据机械臂连杆的几何参数和关节的角度矢量,求出机械臂末端相对于基坐标系的位置和姿态,是关节空间到笛卡尔空间的转换。
采用连杆坐标系变换的方法对史陶比尔RX-90机械臂进行正解。机械臂相邻连杆i-1和连杆i之间的关系可表示为:
(1)
式中cθi=cosθi,sαi-1=sinαi-1等。
机械臂端部对基座的关系0T6可表为:
(2)
根据D-H参数表、式(1)、(2)解得:
(3)
其中:c23=cos(θ2+θ3),s23=sin(θ2+θ3)。
2机械臂工作空间求解
2.1蒙特卡洛法与LHS对比
蒙特卡洛法和LHS都是抽样统计模拟法,是一种以概率统计为理论指导的适用于计算机的数值计算方法[8],核心思想是将确定性问题转化为对应概率模型,对概率模型进行相应的统计实验,最后的统计结果就是确定问题的近似解[9]。
蒙特卡洛法是完全随机的,在输入分布的范围内,样本可以落在任何位置,这样一来样本更有可能从发生概率较高的分布区域中抽取,当执行迭代次数少的时候,会导致聚集问题的产生。假设抽取5个样本点,如图2所示。

图2 蒙特卡罗法样本抽取示意
5个所抽取的样本都落在分布的中间,在分布范围外的取值,不作为样本对输出的结果产生影响。由此可见,要保证结果的准确性,必须抽取足够数量的样本点。
而拉丁超立方体抽样是分层抽样技术,在累计概率尺度(0~1)上把样本空间分成相等的区间,然后从每个区间中随机抽取样本,被抽样本强制代表每个区间的值。假设抽取5个样本,如图3所示。
分层数目等于执行的迭代次数,5个分层每个都有一个样本取出,之后这个样本就不再抽取。由于较少的迭代次数,要达到相同准确性的结果,抽样效率和运行时间将大为改善。
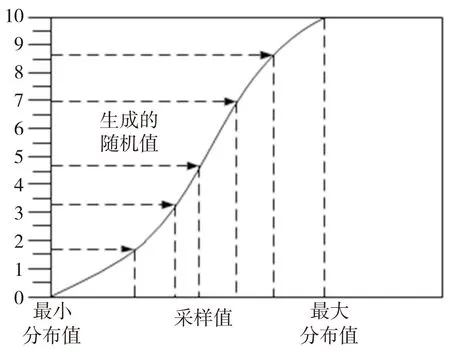
图3 LHS样本抽取示意
2.2LHS求解RX-90工作空间
文献中[10]田海波等采用蒙特卡罗法,选取80000个点求解了六自由度排爆机械臂的工作空间,得到了较为准确的结果。本文采用拉丁超立方体抽样进行工作空间的分析,提高了计算效率,仅需要选取N=10000个点。步骤如下:
(1)因为机械臂末端空间位置与关节θ1,θ2,θ3有关,所以选取N个抽样点时,该立方体为C3=[0,1]3。将3个维度的坐标区间[0,1]分成N等分,每个子区间[(i-1)/N,i/N]标记为i。
(2)设第j维坐标的N个标记的随机排列为(π1j,π2j,…πnj),j=1,2,3。三个维度的3个随机排列相互独立。
(3)取cij为(πij+uij-0.5)/N,i=1,2,…N,uij是[-0.5,0.5]上的均匀分布样本,独立同分布且与π独立。
(4)根据表一参数各关节变量随机取值为
θji=θjmin+(θjmax-θjmin)cij
j=1,2,3;i=1,2,…N
(4)
(5)将式(4)所得每个关节的N个随机变量代入式(3),求得机械臂末端相对应的空间位置向量,将所有向量在Matlab上仿真显示,得到如图4所示工作空间点云图及计算结果。

图4 机械臂可达空间三维点云图

2.3工作空间求解结果的MATLAB验证
在MATLAB环境下,运用机器人工具箱建立史陶比尔RX-90机械臂模型,如图5所示:
采用工具箱中的函数link和robot建立机械臂对象,因本文采用的是改进的D-H法,故link函数的设置参数应选为’mod’。使用LINK.qlim来设定每个关节旋转角度theta的取值范围,如图5a。用drivebot函数驱动生成机械臂,从图5b中可以看出,建立的6R机器人模型与实际相符。
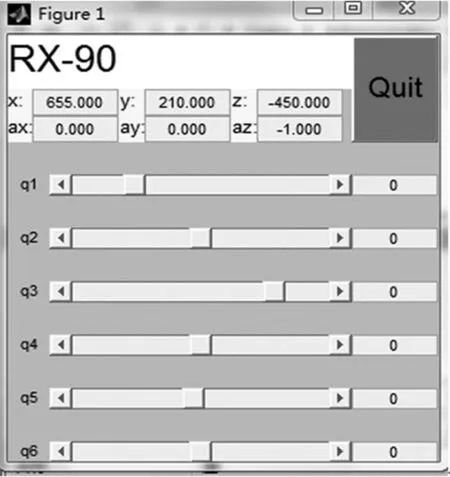
(a)各关节旋转范围限制的设定
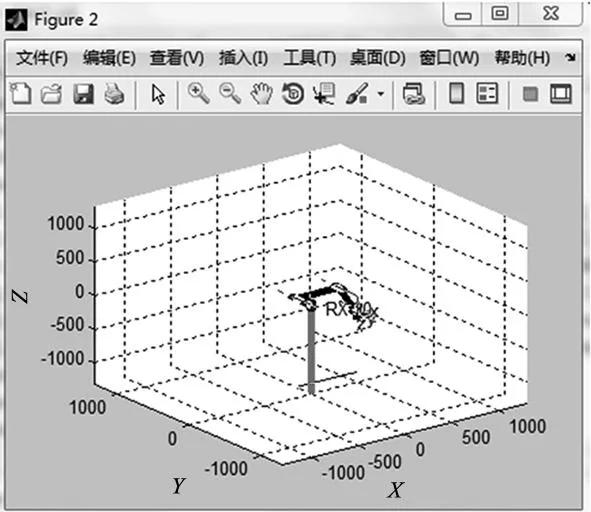
(b)6-DOF机械臂模型生成

(a)X=-965时的边界验证

(b)机械臂正常驱动到达目标位置

(c)X=-975时的边界验证
文章采用随机选取空间位置点的方法来验证所得工作空间范围的正确性。根据LHS分层抽样思想,在[-1000,1000]mm范围内,对X,Y,Z轴每100mm的间距取两个点作为代表,并对三轴坐标轴随机组合得到空间位置点。如果该点在工作空间内,则能通过反解函数ikine和绘图函数plot驱动机械臂从初始点转动至该点,反之则MATLAB报错。考虑到本文的篇幅,仅以边界位置点作为说明,X负轴边界限验证情况如图6所示。
随机选取初始点(300,-300,-350),如图6a,当目标位置点为(-965,-100,0)时,机械臂能正常驱动,从初始位置运动到图6b的位置。而当目标位置点为(-975,-100,0)时,计算结果显示’Solutionwouldn’tconverge’,方法不能收敛,无法驱动机械臂。可见机械臂在X负轴上可得到的下限在(-975,-965)之间,相对误差限为:
同理可得X轴上限,Y、Z轴上下限的范围,从而验证了通过LHS法所得的工作空间点云图的正确性。
3总结
(1)采用D-H法建立坐标系,运用连杆坐标系法求得机械臂运动学正解,获得了机械臂末端位置向量与各关节角位移的关系。
(2)对比了蒙特卡洛法和拉丁超立方抽样(LHS)的抽样理念,得出结论LHS的抽样方法所抽取的样本更具有普遍性,且具有更高的计算效率。
(3)采用了LHS求解了RX-90机械臂的工作空间,在Matlab环境中得到了准确直观的点云图,并使用MATLAB工具箱仿真验证了结果的正确性。为后续机械臂轨迹规划及优化、动力学分析、运动精度控制、系统优化等研究方向提供了参考依据。
[参考文献]
[1] 曾孔庚. 工业机器人技术发展趋势[J]. 机器人技术与应用,2006(6):10-13.
[2]JohnJ.Craig.机器人学导论[M]. 贠超,译.北京:机械工业出版社,2006.
[3] 田海波,马宏伟,魏娟. 串联机器人机械臂工作空间与结构参数研究[J]. 农业机械学报,2013,44(4):196-201.
[4] 张明,何庆中,王志鹏,等, 关节型码垛机器人的工作空间分析[J]组合机床与自动化加工技术,2013(7):68-74.
[5] 何价来,罗金良,宦朋松,等. 基于蒙特卡洛法的七自由度拟人机械臂工作空间分析[J]. 组合机床与自动化加工技术,2015(3):48-51.
[6] 陈泓伍. 水下清刷机械手的设计与分析[D].杭州:浙江大学,2014.
[7] 蔡自兴.机器人学[M].北京:清华大学出版社,2000.
[8]RastegarJ,FardaneshB.ManipulatorworkspaceanalysisusingtheMonteCarlomethod[J].Mechanism&MachineTheory,1990,25(2):233-239.
[9] 梁喜凤,王永维,苗香雯,等.番茄收获机械手工作空间分析与仿真[J].浙江大学学报:农业与生命科学版,2005,31(6):807-811.
[10] 田海波,马宏伟. 井下排爆机器人机械臂运动学及工作空间的分析[J]. 矿山机械,2012(9):105-108.
(编辑赵蓉)
文章编号:1001-2265(2016)07-0030-04
DOI:10.13462/j.cnki.mmtamt.2016.07.009
收稿日期:2015-07-30
作者简介:杜健超(1990—),男,江西宜春人,中国计量学院硕士研究生,研究领域为机械臂轨迹规划算法,(E-mail)448757169@qq.com。
中图分类号:TH113;TG659
文献标识码:A
Workspace Analysis of 6-DOF Robotic Arm Based on Latin Hypercube Sampling
DU Jian-chao,SUN Wei-hong,MA Guan-yu
(CollegeofMechanicalandElectricalEngineering,JiLiangUniversity,Hangzhou310018,China)
Abstract:For the solving of workspace of 6-DOF RX-90 robot manipulator, propose a statistical calculation base on latin hypercube sampling. Establish the mathematical medol of 6-robotic arm joint systems by D-H method. Use the link coordinate transformation to get its forward kinematical parse. Compare the Monte Carlo method and Latin Hypercube Sampling(LHS), according to the relationship of Cartesian space and joint space. Design a way of LHS to analyse the workspace of robotic arm, show its point cloud atlas in Matlab by computer output device and the range of every coordinates. Verify the correctness and validity of result by simulating with matlab robotic tool box. Provide a reference for further study for trajectory planning and optimization, dynamic analysis, precision motion control, system optimization and so on.
Key words:6-DOF robotic arm;latin hypercube sampling;monte carlo method

