面向模糊多级特征的F-MEWMA控制图研究

周　娟,余忠华,侯　智

(浙江大学 浙江省先进制造技术重点研究实验室,浙江 杭州310027)



面向模糊多级特征的F-MEWMA控制图研究

周娟,余忠华,侯智

(浙江大学 浙江省先进制造技术重点研究实验室,浙江 杭州310027)

摘要:围绕难以定量测量、但可以分级量化的质量特性,在实施统计过程控制中所遇到的检出力受限问题展开讨论,提出模糊多变量指数加权移动平均控制图(F-MEWMA)方法.该方法借助于模糊理论,对分级量化特征进行模糊化处理. 针对不同α截集包含信息量多寡的问题,提出应用加权α截集模糊区间值来构造统计量,分别针对模糊单变量和模糊多变量质量特性进行数学表征与比较分析. 采用Matlab仿真的方式确定不同权重系数和不同维数下的控制限,完成F-EWMA、F-MEWMA的设计. 采用Matlab仿真的方法,以识别变异的概率为评价指标对F-MEWMA的监控效果进行分析. 以电能表潜动和起动的质量特性为例,对提出的方法进行应用,取得了较好的应用效果.

关键词：模糊多级特征；模糊理论；模糊多变量指数加权移动平均控制图(F-MEWMA)；加权α截集模糊区间值；识别变异的概率

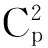
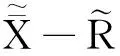
相互关联的多个变量模糊分级特征的控制图研究尚不多见.Shahram等[6]提出通过回归模型分析模糊响应变量和预测变量之间的关系来监控模糊多变量质量特性,Hossein等[7]首次提出了模糊多变量指数加权移动控制图的设计想法.Shahram等[6]针对多个变量测量不准确的问题,Hossein等[7]仅提出设计框架.Ahmadabadi等[8-10]的研究表明,无论单个变量是否存在相关关系,都不能用单个变量的个别控制代替多个变量的联合控制.Juran认为“质量就是适用性”,本文将模糊理论引入,质量的“适用性”标准被表示为模糊集的形式,通过构建有代表性的模糊特征量,并将传统的EWMA控制图扩展为多变量的形式,设计了面向多级模糊特征的多变量F-MEWMA控制图．

1模糊控制统计量的表征及计算

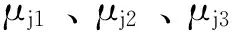
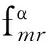
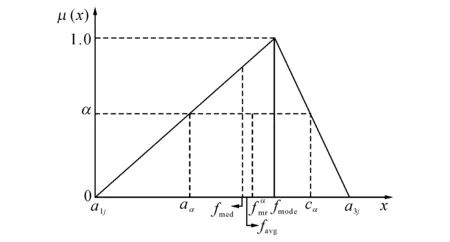
图1　模糊数据集中程度统计量的相互关系Fig.1　Relationships between fuzzy statistics for describing central tendency

(1)

当模糊函数为单峰时,该值唯一.

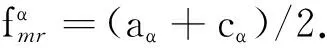
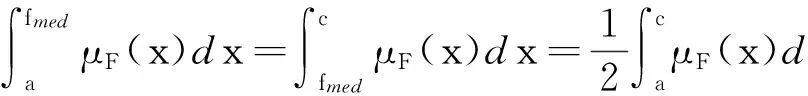
(2)

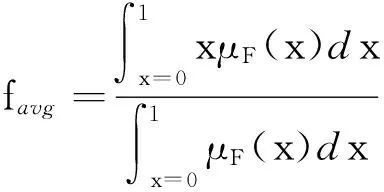
(3)

Taleb在针对彩瓷生产过程中应用多属性变量控制图时,建议为每一个给定的模糊样本分配上面4种代表值中的一种[11].现有研究中提出的模糊代表值方法,可以总结为3类.

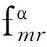
2)将注意力集中在等于或高于α截集的信息,如模糊中位数fmed.

3)对所有α截集信息同等对待,如模糊均值favg.

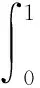
每一个语言变量Cij的模糊集可以用一定的模糊函数μ(Cij)表示,样本A(样本容量为n)可以表示为

A=[[(F11,n11),…,(F1m1,n1m1)];…[(Fi1,ni1)，…，(Fij,nij)];[(Fp1,np1),…，(Fpmp,npmp)]].

式中： nij(其中i=1,2,…,p,j=1,2,…,mp)为第i个变量的第j个类别对应的样本数量,Fij表示第i个变量的第j个类别特性值. 假如第i个变量用mi级模糊语言表示,每个级别的模糊语言对应的模糊三角函数分别为[μ11,μ12,μ13],[μ21,μ22,μ23],…,[μmi1,μmi2,μmi3],则第k个样本的第i个特性的代表性三角函数表示为

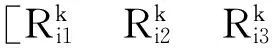
(4)

第k个样本的第i个变量的加权α截集模糊区间值为

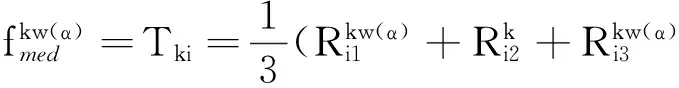
(5)

式中：

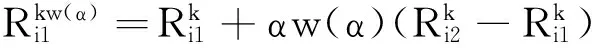
(6)

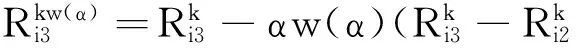
(7)

第k个样本p个特性的模糊特性值可以表示为

Tk=[Tk1,Tk2,…,Tkp].

(8)

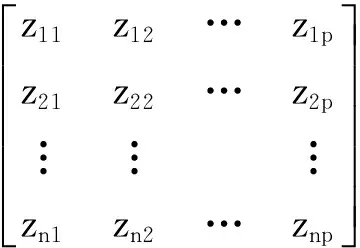
n个样本的模糊特性值可以表示为

(9)

EWMA控制图和CUSUM(cumulative sum)累积和控制图相对休哈特控制图而言,对前期样本赋予不同的权重,利用了更多信息,因而对小波动更加敏感.在使用过程中,研究人员逐渐认识到,CUSUM控制图虽然考虑被控系统时域信息,但没有考虑不同时刻的观察值反应系统质量信息多寡不相同的原则.EWMA控制图的权重随着观测时间的推移越来越小,而且减小的趋势可以通过平滑系数λ加以改变,以适应不同加工过程的特点. 本文在指数加权移动平均控制图的基础上,设计了F-MEWMA控制图．

2F-MEWMA控制图的设计

F-MEWMA控制图的设计按照构建F-EWMA的统计量、构建F-MEWMA的统计量、构建控制限的步骤进行．

2.1构建F-EWMA的统计量

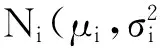
EWMA控制图的理论基础为正态分布,故在作F-EWMA控制图前须对转换后的数据进行正态性检验.若不符合,则可以进行正态性(Box-Cox)转换．

2.2构建F-MEWMA的统计量

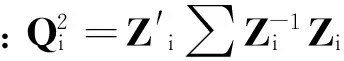
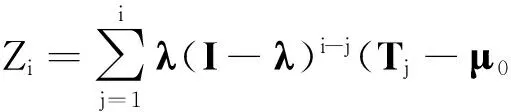
(10)

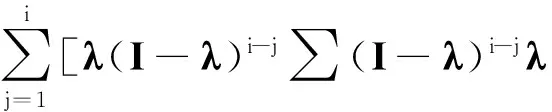
(11)

I和λ都是对角阵,所以协方差矩阵∑Zi的第(k,l)个元素为

若λ1=λ2=…=λp=λ,则协方差矩阵∑Zi的第(k,l)个元素可以简写为

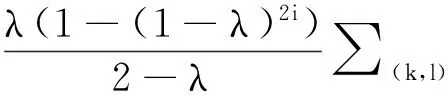
即

当i→∞时,

2.3计算控制图的控制限；

对于单变量F-EWMA控制图,统计量Zi的期望和方差为

E(Zi)=(1-λ)iμ+E(λZi-1)=μ,

(12)

(13)

当i→∞时,

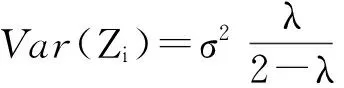
(14)

当i较小(即样本序号较少)时,控制图的控制限的通式为

(15)

当i较大(即样本序号较多)时,则式(15)可以转化为

(16)

表1不同权重系数λ下的控制限H(p=2)

Tab.1ControllimitsHfordifferentweightcoefficientsλ(p=2)

λHλH0.18.650.410.320.29.680.510.530.310.09——

表2不同权重系数λ下的控制限H(p=3)

Tab.2ControllimitsHfordifferentweightcoefficientsλ(p=3)

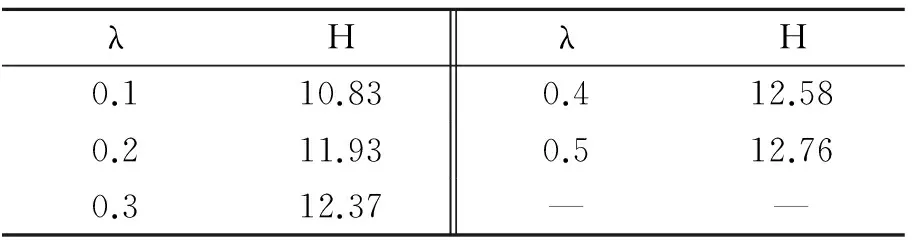
λHλH0.110.830.412.580.211.930.512.760.312.37——

表3不同权重系数λ下的控制限H(p=4)

Tab.3ControllimitsHfordifferentweightcoefficientsλ(p=4)

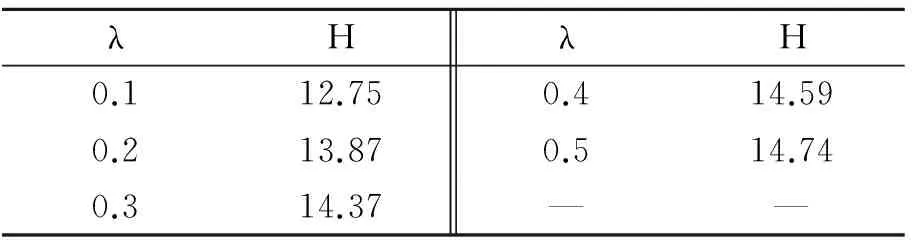
λHλH0.112.750.414.590.213.870.514.740.314.37——

权重系数λ的确定可以按照如下步骤进行.1)根据上述仿真结果,采用回归分析的方法确定H与λ的回归方程；2)在不同维数p下,给定不同的λ,选取不同H(λ确定,H确定)仿真计算出不同偏移量ξ(实际中允许的值)下的ARL；3)通过回归分析,确定ARL与λ的回归方程(ξ一定)；4)找出ARL与λ的回归方程(ξ一定)中最小ARL对应的λ.具体的实现过程参见文献[16].

3F-MEWMA性能分析

以构造的新统计量为2维变量为例,以识别变异的概率为指标展开仿真分析.假设过程均值向量发生偏移,方差向量不变.用Matlab产生200个样本,前100个样本均值向量为μ0,后100个样本均值向量为μ′0.按照2.3节中控制图控制限的确定方法确定H,选取λ与H的对应关系,如表1所示.针对过程均值向量发生不同偏移ξ,运用Matlab进行仿真,作出F-MEWMA控制图,统计失控点的数目mi,对每种不同偏移ξ运行5 000次,求出识别变异的概率为

当λ=1时,F-MEWMA控制图变为F-T2控制图.为了对比分析,作出F-T2控制图并计算识别变异的概率.在计算程序中,F-T2的样本量n=200.计算结果如表4所示.可以看出,对于F-MEWMA,λ越小,相应的p越大,控制图越灵敏.F-MEWMA的p均比F-T2的p大,说明新设计的F-MEWMA比F-T2更加灵敏．

4F-MEWMA案例应用分析

电能表是电能计量、线损考核的计量器具,电能表的测量值是否准确将直接影响电费收取的公平公正.电能表的潜动不良和起动不良是2个发生频次较高并且相关的不良项目.潜动是指电能表各电流线路无负载电流,各电压线路加80%～110%的参比电压, 电能表的转盘转动应少于1转.由于制造、装配、维修时造成的磁路不对称的情况, 产生固有的补偿力矩, 该力矩称为附加潜动力矩.当附加补偿力矩超过摩擦力矩, 电能表在无负荷电流时, 转盘会不停地转动, 从而形成潜动.企业检验“潜动”这一特性时观察电能表无负荷电流时转1/4圈内、1/4圈～1/2圈、1/2圈～1圈、1圈以上的情况.分别表示为：T(C1=潜动)={C11,C12,C13,C14}={很好,好,一般,不合格}.所谓起动是指电能表在参比频率、参比电压和cosφ=1(对有功电能表) 或sinφ=1(无功电能表) 的条件下,电能表电流线路通以规定的起动电流(三相电能表各相同时加电压和通电流),转盘应连续转动.这一指标反映了电能表灵敏度的高低.企业检验“起动”这一特性时观察电能表15 s内转1圈、15～30 s时转1圈、30～60 s时转1圈、60 s未转1圈的情况.分别表示为

T(C2=起动)={C21,C22,C23,C24}={很好,好,一般,不合格}．

电能表的潜动和起动是衡量计量性能的重要指标.是否满足规程要求, 是电能表能否正确计量电能的关键.将电能表的潜动和起动情况进行统计,如表5所示. C1的模糊函数如图2所示,C2的模糊函数如图3所示．

图2　潜动模糊函数Fig.2　Creeping fuzzy function

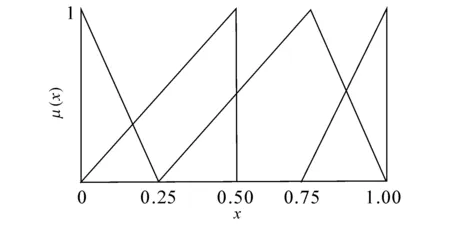
图3　起动模糊函数Fig.3　Starting fuzzy function

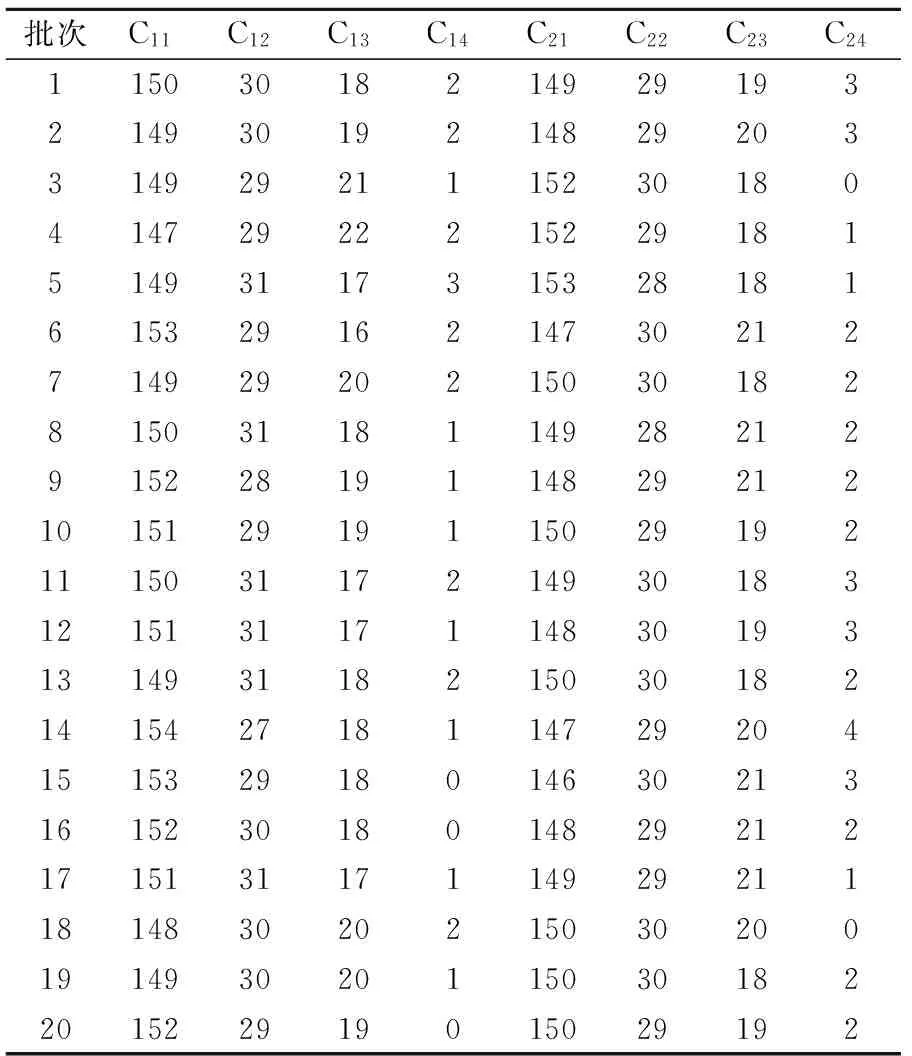
批次C11C12C13C14C21C22C23C24115030182149291932149301921482920331492921115230180414729222152291815149311731532818161532916214730212714929202150301828150311811492821291522819114829212101512919115029192111503117214930183121513117114830193131493118215030182141542718114729204151532918014630213161523018014829212171513117114929211181483020215030200191493020115030182201522919015029192

对表5中的数据,按照提出的方法计算第1个样本号的第1个特性,本例中α=0.6,w(α)=3α2．

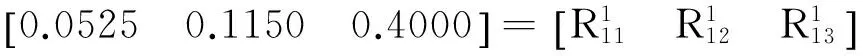
0.052 5+0.65×(0.115 0-0.052 5)=0.093 1,

0.400 0-0.65×(0.400 0-0.115 0)=0.215 0,

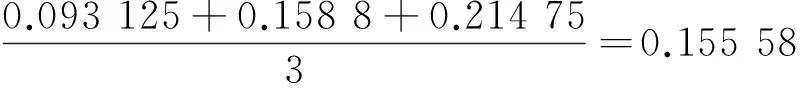
取λ=0.1,可以计算出Z11=λT11+(1-λ)Z0=0.141 78．

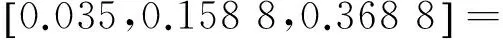
0.035+0.65×(0.158 8-0.035)=0.115 5,

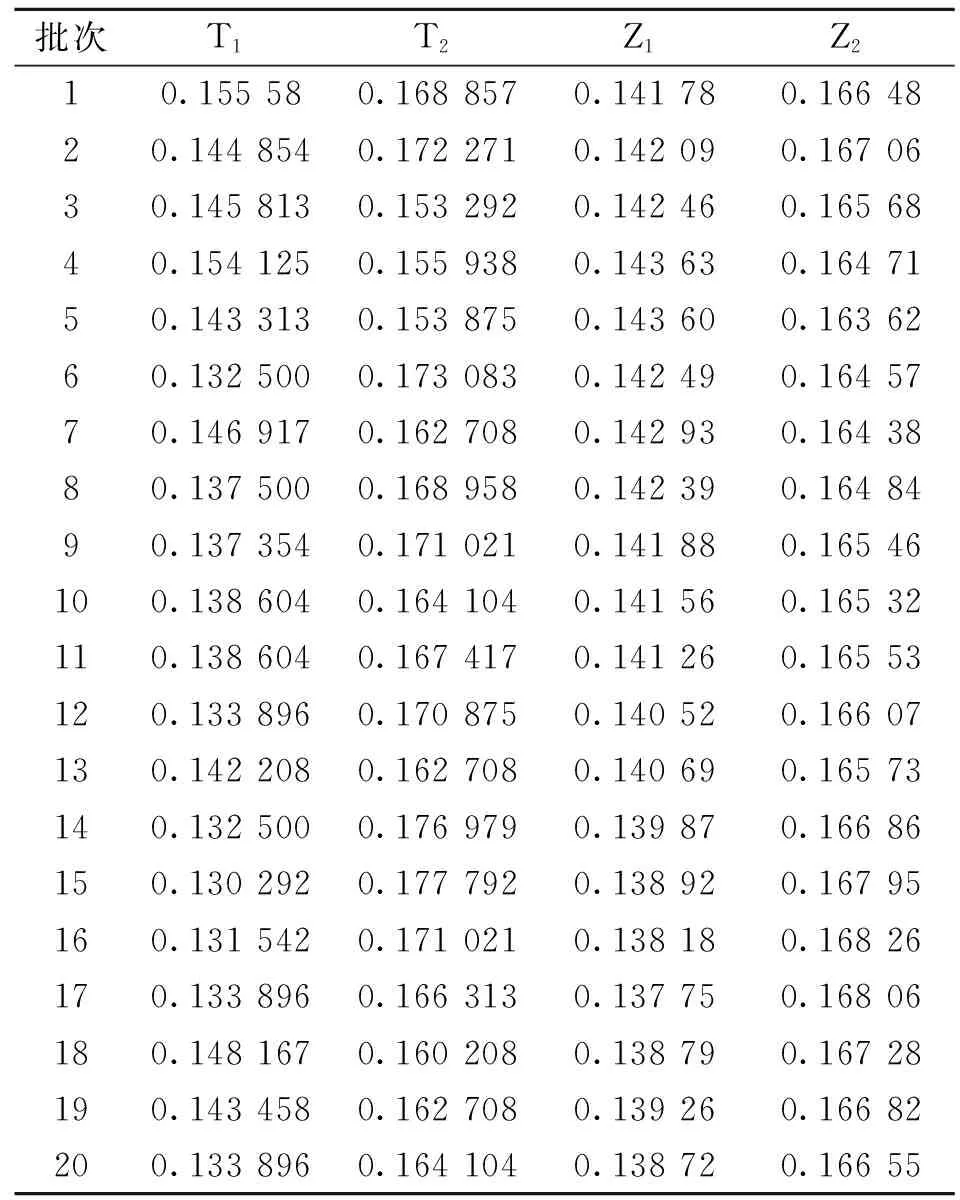
表6　模糊统计量计算结果

0.368 8-0.65×(0.368 8-0.158 8)=0.232 3,

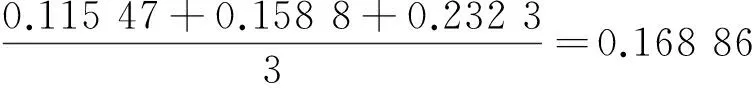
Z12=λT12+(1-λ)×Z0=0.166 48.

对变量1、2的正态性检验如图4、5所示.图中，Pad为Anderson-Darling提出的P统计量.由图4、5可以看出,变量1、2均服从正态分布,无需进行Box-Cox变换,可以直接作出图6所示的F-MEWMA控制图.变量1和变量2的F-EWMA分别如图7、8所示. 如图9、10所示分别为变量1和变量2的不合格品率控制图(p图),如图11所示为F- T2控制图．

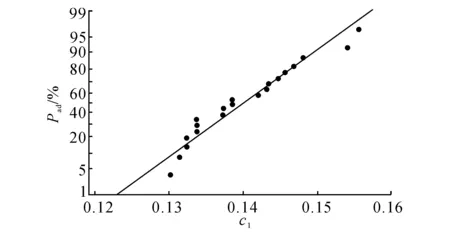
图4　变量1的正态性检验Fig.4　Normal inspection for variable 1

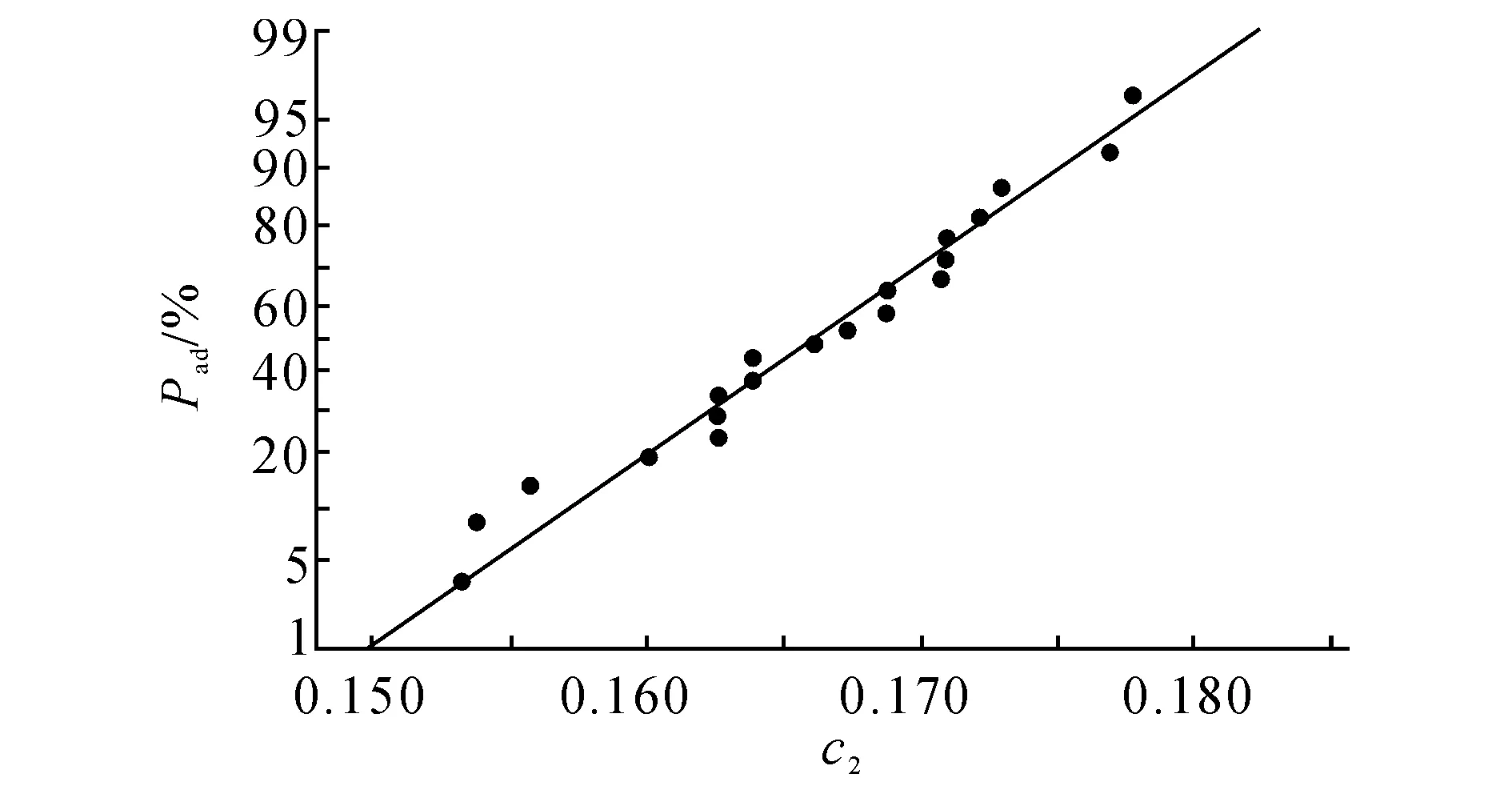
图5　变量2的正态性检验Fig.5　Normal inspection for variable 2

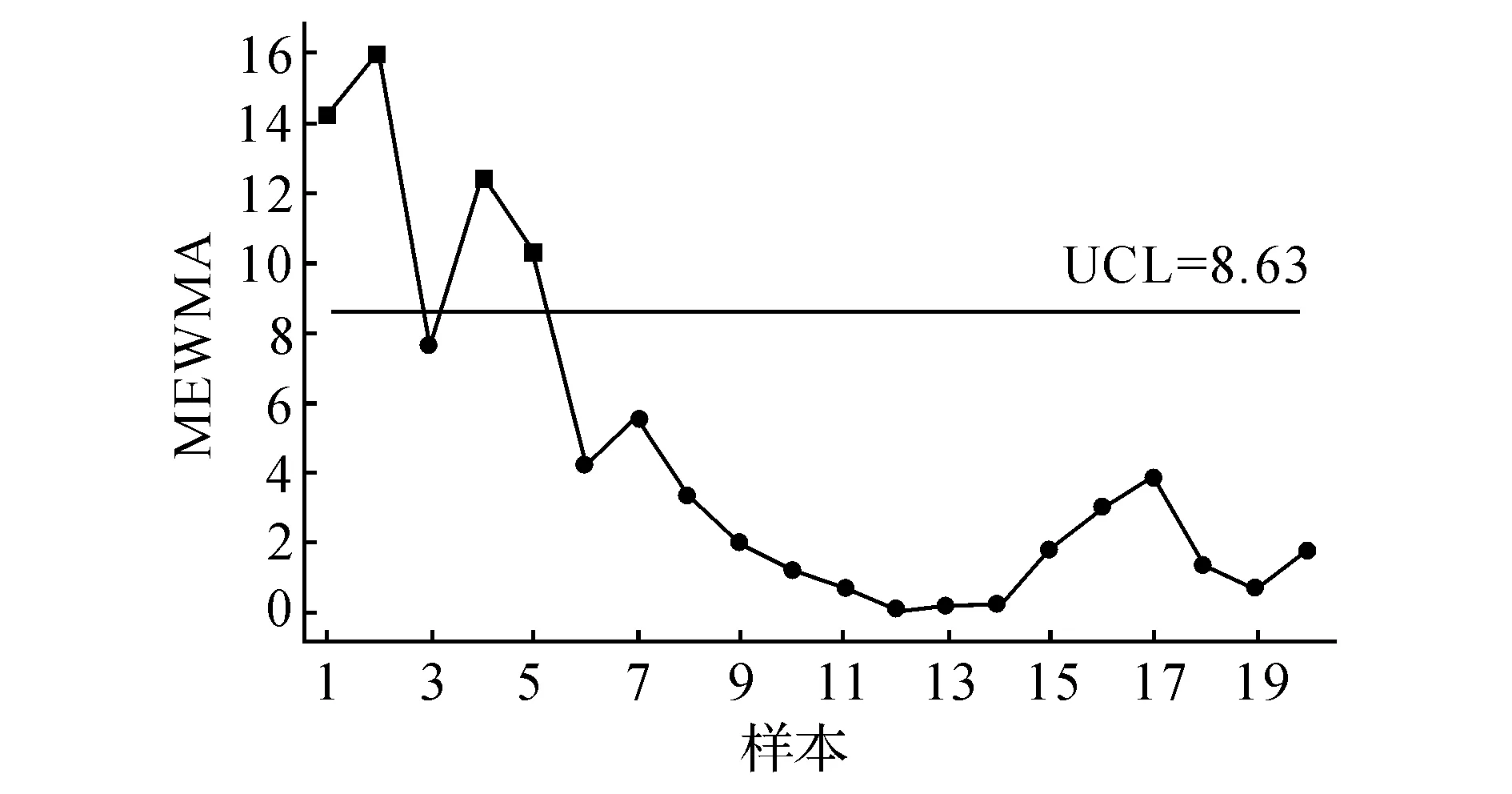
图6　F-MEWMA控制图Fig.6　F-MEWMA control chart

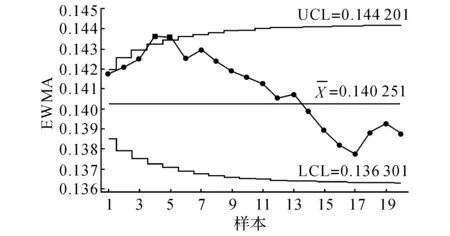
图7　变量1的F-EWMA控制图Fig.7　EWMA control chart for variable 1

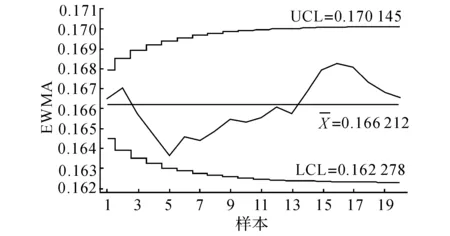
图8　变量2的F-EWMA控制图Fig.8　EWMA control chart for variable 2

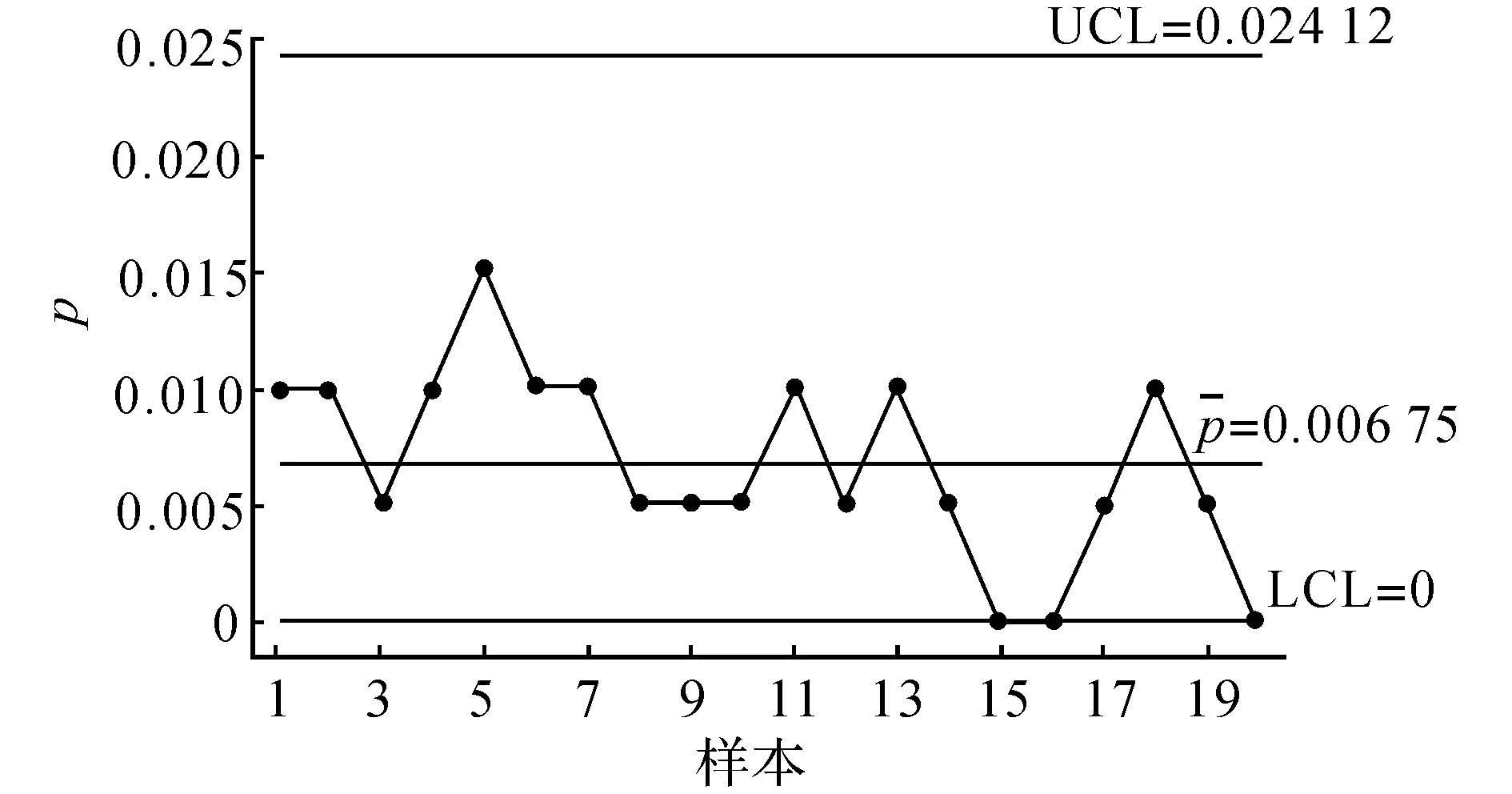
图9　变量1的p控制图Fig.9　pcontrol chart for variable 1

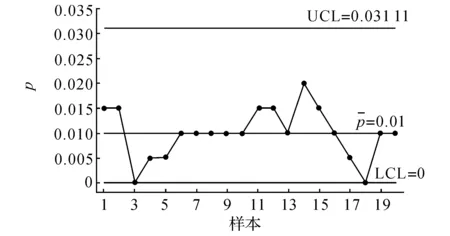
图10　变量2的p控制图Fig.10　pcontrol chart for variable 2

图11　F-T2控制图Fig.11　F-T2 control chart

分析图6～11得出如下结论.

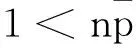
2)图6显示,样本号1、2、4、5均显示失控.由图7的变量1即潜动的F-EWMA控制图看出,样本号4、5显示失控.由图8的变量2即起动的F-EWMA控制图看出,未显示失控.说明新设计的F-MEWMA和F-EWMA体现了单个变量的个别控制不能代替多个变量的联合控制的原则；图11仅显示样本号1失控,说明F-MEWMA的灵敏性优于F-T2控制图．

5结论

(1)针对模糊多级特征的多个质量特性的控制问题,提出借助模糊理论设计面向模糊多级特征的F-MEWMA控制图的方案.由于该方法充分地利用了分级量化所揭示的信息,并且包含了多变量之间的统计关系,从而可以提高控制图的检出力及降低对样本量的要求.

(3)引入传统的单变量指数加权移动平均控制图EWMA方法,将其扩展为多变量的形式,设计了面向多级模糊质量特性的F-MEWMA控制图.重点对控制限的确定、控制图的性能进行讨论.

(4)电能表潜动和起动特性现场监控算例结果表明,新设计的多变量F-MEWMA控制图对于控制模糊多变量的质量特性具有较好的性能．

参考文献(References)：

[1]ZARANDIH,MOHOHAMMADHF.Ageneralfuzzy-statisticalclusteringapproachforestimatingthetimeofchangeinvariablesamplingcontrolcharts[J].InformationSciences, 2010, 180(16): 3033-3044.

[2]GULBAYM,KAHRAMANC.Analternativeapproachtofuzzycontrolcharts:directfuzzyapproach[J].InformationSciences, 2007, 177(8): 1463-1480．

[4]SENTURKS.Fuzzyregressioncontrolchartbasedonα-cutapproximation[J].InternationalJournalofComputationalIntelligenceSystems, 2010, 3(1): 123-140．

[5]侯世旺,同淑荣. 基于模糊数的不确定质量控制图及选型[J]. 计算机集成制造系统,2012, 18(2): 415-421．

HOUShi-wang,TONGShu-rong.Fuzzynumber-baseduncertainqualitycontrolchartandtypeselection[J].ComputerIntegratedManufacturingSystems, 2012, 18(2): 415-421．

[6]SHAHRAMG,KAZEMN,RASSOULN.Developingamultivariateapproachtomonitorfuzzyqualityprofiles[J].QualityandQuantity, 2014, 48: 817-836.

[7]HOSSEINA,RASSOULN.Fuzzymultivariateexponentiallyweightedmovingaveragecontrolchart[J].InternationalJournalofAdvancedTechnology, 2010, 48(9)：1001-1007．

[8]AHMADABADIM,FARJAMIY,MOGHADAMM.Aprocesscontrolmethodbasedonfive-parametergeneralizedlambdadistribution[J].QualityandQuantity, 2012, 46: 1097-1111．

[9]葛志强,宋执环,杨春节. 基于MCUSUM-ICA-PCA的微小故障检测[J]. 浙江大学学报：工学版,2008,42(3)：373-377．

GEZhi-qiang,SONGZhi-huan,YANGChun-jie.SmallshiftdetectionbasedonMCUSUM-ICA-PCA[J].JournalofZhejiangUniversity:EngineeringScience, 2008,42(3): 373-377．

[10]PILLETM,BOUKARA,PAIRELE.MultivariateSPCfortotalinertialtolerancing[J].InternationalJournalofMetrologyandQualityEngineering, 2013, 4(3): 169-175．

[11]TALEBH.Controlchartsapplicationsformultivariateattributeprocesses[J].ComputersandIndustrialEngineering, 2009, 56(1): 399-410．

[12]HRYNIEWICZO.Statisticswithfuzzydatainstatisticalqualitycontrol[J].SoftComputing, 2008, 12(1): 229-234．

[13]RUNGERGC,PRABHUSS.AMarkovchainmodelforthemultivariateexponentiallyweightedmovingaveragescontrolchart[J] .JournaloftheAmericanStatisticalAssociation, 1996, 91(436):1701-1706．

[14]LOWRYCA,WOODALLWH,CHAMPC.Amultivariateexponentiallyweightedmovingcontrolaveragecharts[J].Technometrics, 1992, 34(1): 46-53．

[15]MOLNAUWE,RUNGERGC,MONTGOMERYDC.AprogramforARLcalculationformultivariateEWMAchart[J].JournalofQualityTechnology, 2001, 33(4): 515-521．[16]杜褔洲,唐晓青,孙静.MEWMA控制图ARL计算及参数优化[J]. 北京航空航天大学学报,2006,32(8)：974-978．

DUFu-zhou,TANGXiao-qing,SUNJing.ARLcomputationandparametersoptimizationforMEWMAcontrolchartbasedontheMarkovchain[J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2006,32(8)：974-978.

收稿日期：2015-05-20.浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

基金项目：国家自然科学基金资助项目(50835008,71071138).

作者简介：周娟(1979-)，女，讲师，博士生，从事质量工程的研究.ORCID: 0000-0002-2579-0067.E-mail:happyzhoujuan@126.com 通信联系人：余忠华，男，教授，博导. ORCID: 0000-0003-3326-5526. E-mail:yuzhh@zju.edu.cn

DOI:10.3785/j.issn.1008-973X.2016.07.021

中图分类号：O 213

文献标志码：A

文章编号：1008-973X(2016)07-1373-08

F-MEWMAcontrolchartforfuzzyhierarchicalquantitativecharacteristics

ZHOUJuan,YUZhong-hua,HOUZhi

(Key Laboratory of Advanced Manufacturing Technology of Zhejiang Province, Zhejiang University,Hangzhou 310027, China)

Abstract:Fuzzy multivariate exponentially weighted moving average control chart (F-MEWMA) was proposed in order to solve the problem of lower power when implementing statistical process control to the quality characteristic which was difficult to quantify but could be described in hierarchical levels. F-MEWMA tried to blur the hierarchical quantitative characteristics based on fuzzy theory. Since different α cut sets containing different amount of information, interval value of weighted fuzzy α cut set was proposed. Mathematical characterization and comparison of the quality characteristics for fuzzy univariate data and fuzzy multivariate data were conducted respectively, and the control limits for different weight coefficients and different dimensions were determined by Matlab simulation. Then F-EWMA and F-MEWMA were designed. The effect of F-MEWMA was analyzed by calculating probability of identifying variation by Matlab simulation. The implementation of the F-MEWMA on the electric energy meter running and starting quality characteristics showed good result．

Key words:fuzzy hierarchical quantitative characteristic; fuzzy theory; fuzzy multivariate exponentially weighted moving average control chart (F-MEWMA); interval value of weighted fuzzy α cut set; probability of identifying variation