管网水质多指标动态关联异常检测方法

魏　媛,冯天恒,黄平捷,侯迪波,张光新

(浙江大学 工业控制技术国家重点实验室,浙江 杭州 310027)



管网水质多指标动态关联异常检测方法

魏媛,冯天恒,黄平捷,侯迪波,张光新

(浙江大学 工业控制技术国家重点实验室,浙江 杭州 310027)

摘要:为了提高城市供水管网水质监测系统的污染检测能力,利用污染物所引起多个指标变化之间的关联特性,提出基于多常规水质指标动态关联分析的水质异常检测方法.应用动态时间规整算法(DTW)衡量多个常规水质指标时间序列间的动态距离,刻画各指标波动的相似程度和动态关联特性.利用D-S证据理论融合各指标单独的异常概率,将融合后得到的供水管网水质异常概率与所设定的多指标融合异常概率阈值进行比较,作出当前时刻水质是否存在水质异常的综合判断.依托课题组模拟供水管网实验系统,设计不同浓度的硫酸铜和铁氰化钾污染物的注入实验,利用在线监测的pH值、浊度、余氯、溶解氧等8种常规水质指标进行动态关联分析和水质异常检测,方法的可行性和异常检测性能通过受试者工作特征曲线(ROC)进行验证.

关键词：常规水质指标；数据融合；水质异常检测；时间序列分析；动态时间规整；相关性分析

水是人类赖以生存的自然资源,饮用水的质量与人们生产生活息息相关.城市供水系统中任一环节出现问题,均可能对居民的日常生活用水造成严重影响[1].建立一套能够准确挖掘异常水质状况并及时进行预警处理的饮用水污染预警系统对于保障广大居民的用水安全意义重大.水质异常检测作为后续响应操作的基础,在整个水质预警系统中起着非常重要的作用.

供水管网中的水质监测数据在日常观测中的变化称为水质波动.引起管网水质发生波动的原因包括日常背景变化、工艺操作变化、仪表传输噪声以及水质污染事件等.在水质异常检测中,最受关注的是由于水质污染事件所引起的水质波动,如何能够将因污染物注入所引起的异常变化从常规水质波动中剥离出来,是水质异常检测的核心.

早期的研究主要依据统计学方法,通过判断单一水质指标测量值是否超出背景数据均值3倍标准差的范围来判断是否存在异常[2]；为了克服水质数据本身存在的波动性对检测结果的影响,之后的研究逐渐向时间序列分析的方向过渡[3]；近年来,随着数据挖掘技术的发展,水质异常检测逐渐打破单一参数的束缚,研究人员开始利用机器学习的相关方法将多个传感器的检测结果进行融合,以期达到更好的检测效果.贝叶斯网络[4]、决策树[5]、人工神经网络[6]、支持向量机[7]等有监督的学习算法以及K平均聚类[8]、轨迹聚类[9]、最小椭球体积聚类[10]、多维最近邻聚类[11]等无监督的学习算法都在水质异常检测领域得到了广泛的应用；此外,针对空间分布传感器检测结果的融合逐渐成为研究的热点[12-13].虽然上述研究的方法不同,但结果都体现出了多指标异常检测性能的优势.

多指标水质信息融合并非简单的数据叠加.污染物进入水体后,会引起多个水质指标之间的联动变化,且由于受到水体缓冲、仪器检测原理等因素的影响,各指标对污染物的响应速度及持续时间不同[14].现有的多传感器信息融合的异常检测方法多是通过统计一段时间窗口内出现异常的指标个数来对各指标的决策结果进行直接融合[15-16],往往对于污染物注入前、后指标之间的相关性变化挖掘不够充分,且由于各指标时间序列的波动变化并非完全同步,往往会导致融合后的判断结果存在滞后和误判.

本文针对该问题,提出基于动态时间规整算法的水质异常检测方法.动态时间规整算法是一种将时间规整与距离测度结合起来进行相似性度量的方法.因该算法对序列在时间轴的伸缩、扭曲和异位等形变具有较好的包容性,在语音识别、机器学习等领域的序列相似度比较中得到了很好的应用.本文将动态时间规整算法引入到多水质指标的变化相似度分析中,通过滑动时间窗读取一定长度窗口内各个水质参数的时间序列,利用动态时间规整算法来计算任意两个指标时间序列之间的动态距离,得到两两指标间波动的动态关联系数.利用D-S证据理论的方法融合每个参数各自的基本异常概率,判断当前时刻的水质是否存在异常.该方法旨在通过多指标关联特性的挖掘来提高异常检测的灵敏程度,同时减少因各指标响应速度不同所导致的检测误判和滞后.

1管网水质异常检测算法

水质异常是指一个或多个水质指标在一定时间内所呈现出的偏离正常行为的波动状况[17].由污染物所引起的水质异常通常会造成一个或多个水质指标产生波动,且不同指标的变化之间呈现一定的关联性,这与因传感器故障、仪器传输噪声等因素所引起的水质监测数据波动有着本质的区别.这种关联特性的利用可以在单一指标检测的基础之上,进一步提高异常检测的准确性和灵敏程度.本文将单参数的基本异常概率和多参数的动态关联系数进行融合,通过D-S证据理论的基本概率分配函数定义基于单参数的异常概率,利用动态时间规整算法来计算水质参数两两间的动态关联系数.依据合成规则将单参数层面的异常概率与多参数层面的相关程度进行融合,对当前时刻水质是否存在异常作出综合判断.

1.1单参数基本异常概率计算

对于单指标的时间序列,异常的定义通常是指一段时间内的观测值相对于参考值的偏移程度.本文通过D-S证据理论的基本概率分配函数来定义每个指标(证据)各自的异常概率.

D-S证据理论由Dempster[18]提出,并由Shafer进一步完善[19].D-S证据理论依靠证据(即多源信息)的积累,逐渐缩小假设范围,从而实现多源信息的融合.证据理论最基本的内容包括3个部分：识别框架、基本概率分配函数和合成规则.

识别框架是一个元素可穷举的集合,集合内互斥的各元素代表所有的可能性.在水质异常检测中,识别框架中只包含正常(normal)与异常(abnormal)两个元素.基本概率分配函数是从识别框架的幂集到[0,1]的映射,框架中所有可能性的概率之和为1.在水质异常检测的实际应用中,单参数的基本异常概率须能够反映出水质时间序列在短时间内的动态变化,因此引入短时均方根[20]来衡量水质时间序列在时间窗口内的波动情况.定义基本概率分配函数如下：

(1)

式中：m(Abnornal)为当前时刻该水质指标发生异常的概率；D为当前时刻向前一个时间窗内各个观测值的短时均方根；σ为水质正常波动下历史数据的短时均方根平均值,由历史数据训练而得.当水质时间序列的波动为零时,m(Abnormal)=0；当水质时间序列的波动趋于无穷时,m(Abnormal)=1.定义的单参数的基本异常概率符合实际物理含义.

1.2多参数关联系数计算

在污染物注入系统之后并非所有的监测指标都会有响应.不同的污染物可能会引起不同指标的变化,且各指标的变化之间存在较强的关联性.在将多个指标的检测结果进行融合前,需要引入各个指标之间变化的关联程度.

度量多指标时间序列相关性的主要方法包括Minkowski距离、动态时间规整、奇异值分解和基于点分布特征的方法等[21].动态时间规整算法(dynamictimewarping,DTW) 最早用于语音信号处理方向,由Berndt等[22]引入到时间序列分析中,用于度量两个任意长度的时间序列的相似度.DTW算法对时间序列的同步问题稳健性较好,允许时间序列长度不同,且允许不同步的点进行对应计算,因此对于在时间轴上存在伸缩、扭曲和异位的时间序列,采用该算法能够较好地度量两时间序列之间的相似性.

DTW算法的原理如图1所示,图中,γ为电导率.依据两点间的欧式距离可以构造距离矩阵d.

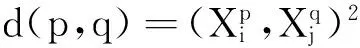
(2)

DTW算法的实质是在所有的点点匹配中寻找一种使得平均距离最短的匹配模式,即

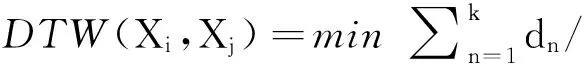
(3)

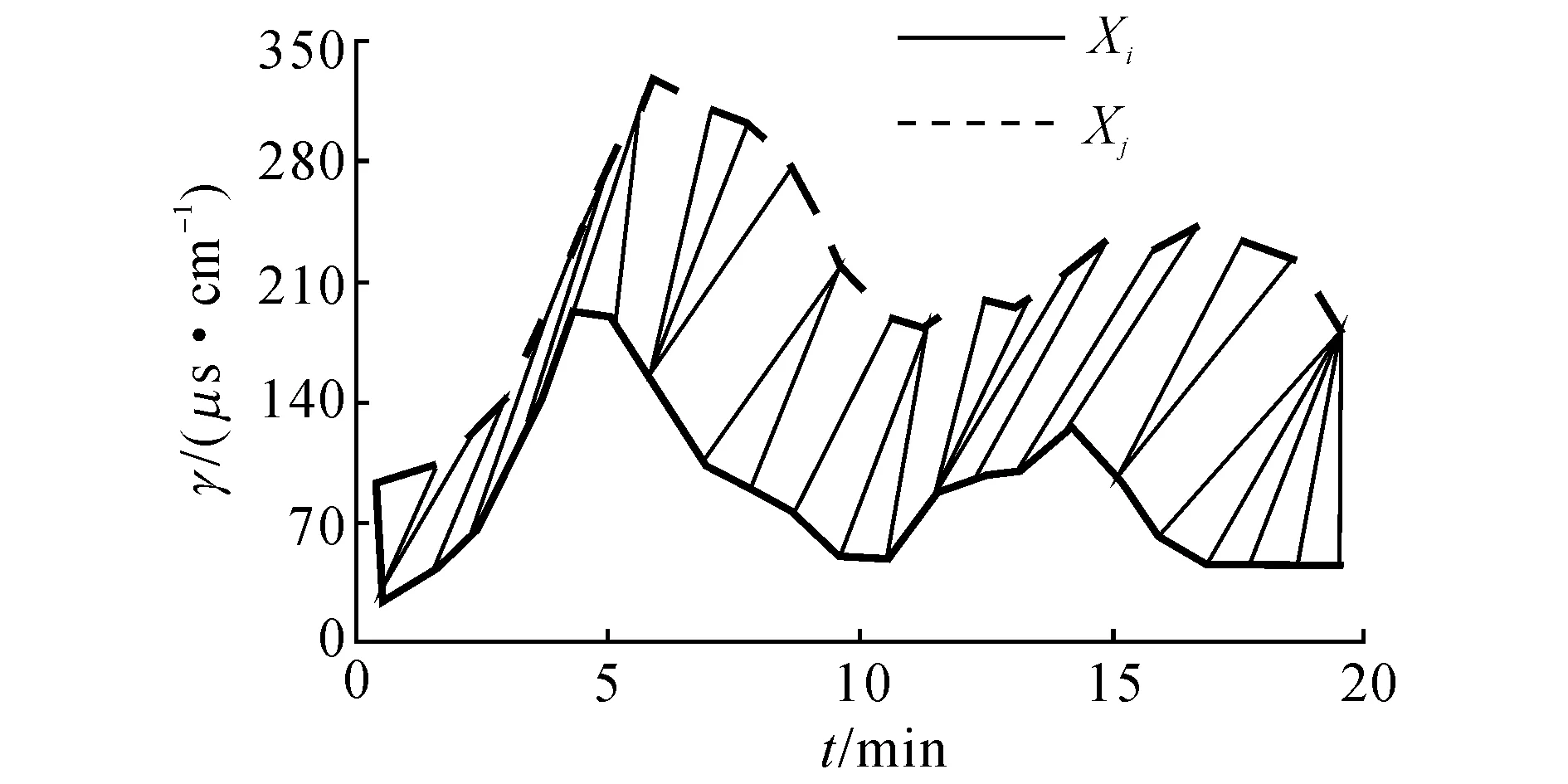
图1　DTW算法原理图Fig.1　Schematic diagram of DTW

考虑到各指标在时间轴上可能存在响应不同步的情形,引入最大允许时间偏差ξ.ξ为两序列对应点进行匹配时最大可以允许的时间轴异位,定义t0时刻两时间序列间在最大允许时间偏差为ξ时的动态距离为

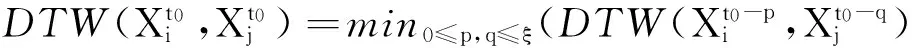
(4)

得到当前时刻两序列的动态距离之后,将该距离值映射到[0,1]内,得到动态关联系数为

(5)

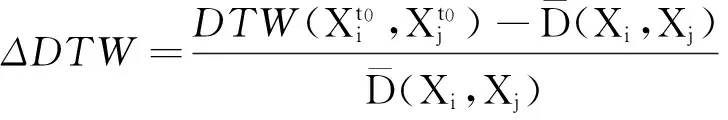
(6)

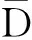
1.3概率合成

合成规则是用于计算同一识别框架下不同证据信息的基本概率融合方法,根据实际情况不同,存在很多不同的合成规则.在水质异常检测中,正常的水质波动情况下各参数的联动性较弱,污染事件通常会引发两种或两种以上水质指标的联动变化,因此本文的概率融合选择将DTW算法得到的任意两参数之间关联系数与两参数各自的单参数基本异常概率进行相乘,得到融合后的异常概率关联矩阵.从矩阵各元素中选取最大值作为当前时刻的水质异常概率,通过与所设定的异常概率报警阈值进行比较,给出当前时刻水质是否存在异常的判断结果.

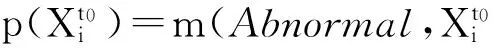
(7)

综上所示,提出的水质异常检测方法计算流程如图2所示.

概率合成规则是取单指标异常概率与多指标关联系数乘积的最大值,因此如果只是单一指标因信号传输故障、瞬时噪声引入等原因导致的波动,不会对乘积结果产生大幅度影响；当两个或两个以上水质指标监测值同时出现大幅波动,且各参数的波动具有较强的相关性时,融合概率有可能超过阈值形成异常报警.这样的融合结果不仅能够利用多参数之间的相关性实现准确的异常挖掘,而且可以有效地避免因传感器噪声、信号干扰等造成的误报,尽量在保证检出率的前提下降低误报率.

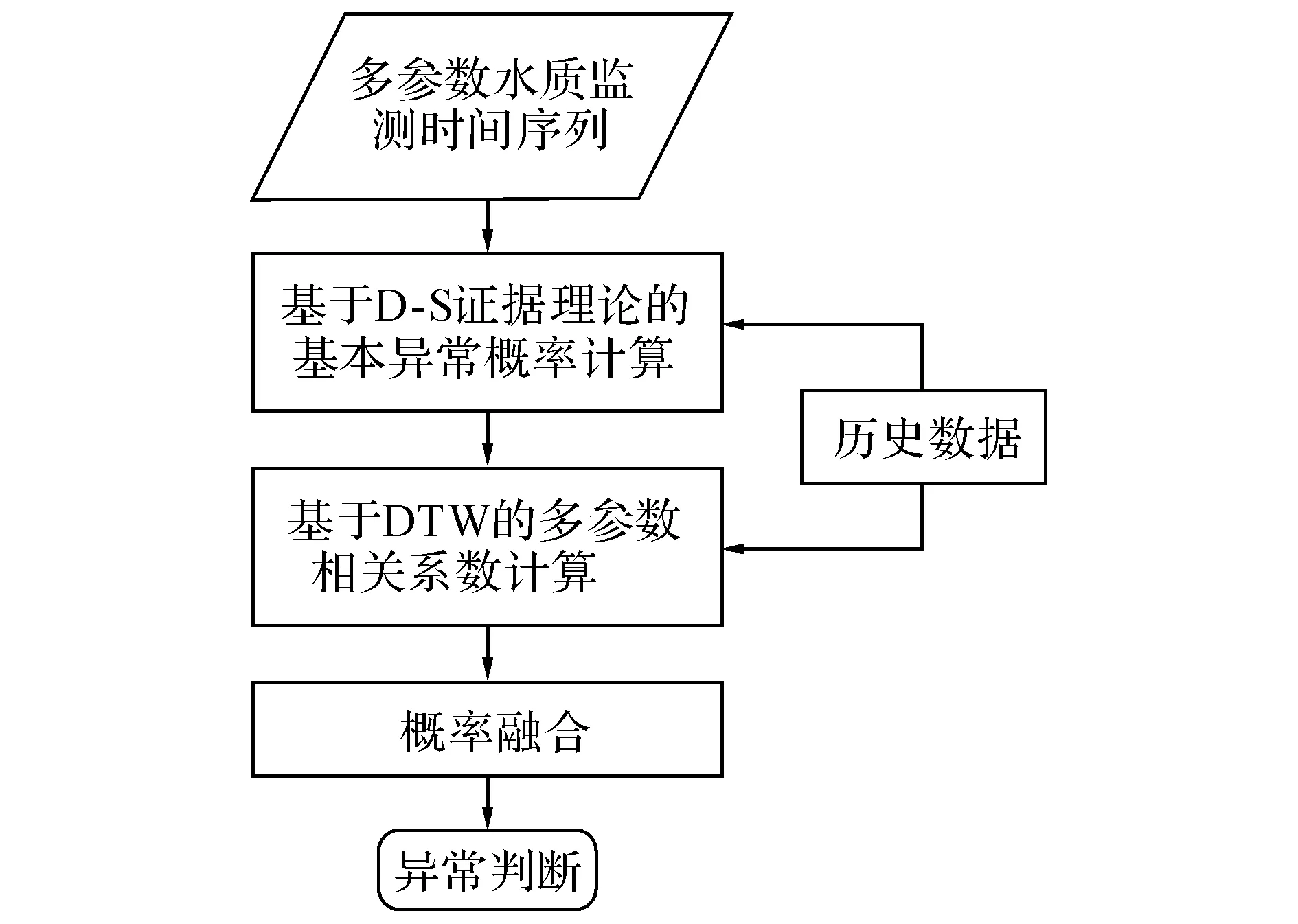
图2　异常判断流程图Fig.2　Anomaly detection flow chart

2管网污染物注入实验

2.1污染物注入实验设计

整个实验是在课题组的供水管网模拟实验系统上进行的.管网构造如图3所示,包括自动加药混合系统以及在线监测系统两个部分.加药过程通过PLC控制加药支路的蠕动泵来实现,全部在线监测仪器都安置在主管路沿线上.

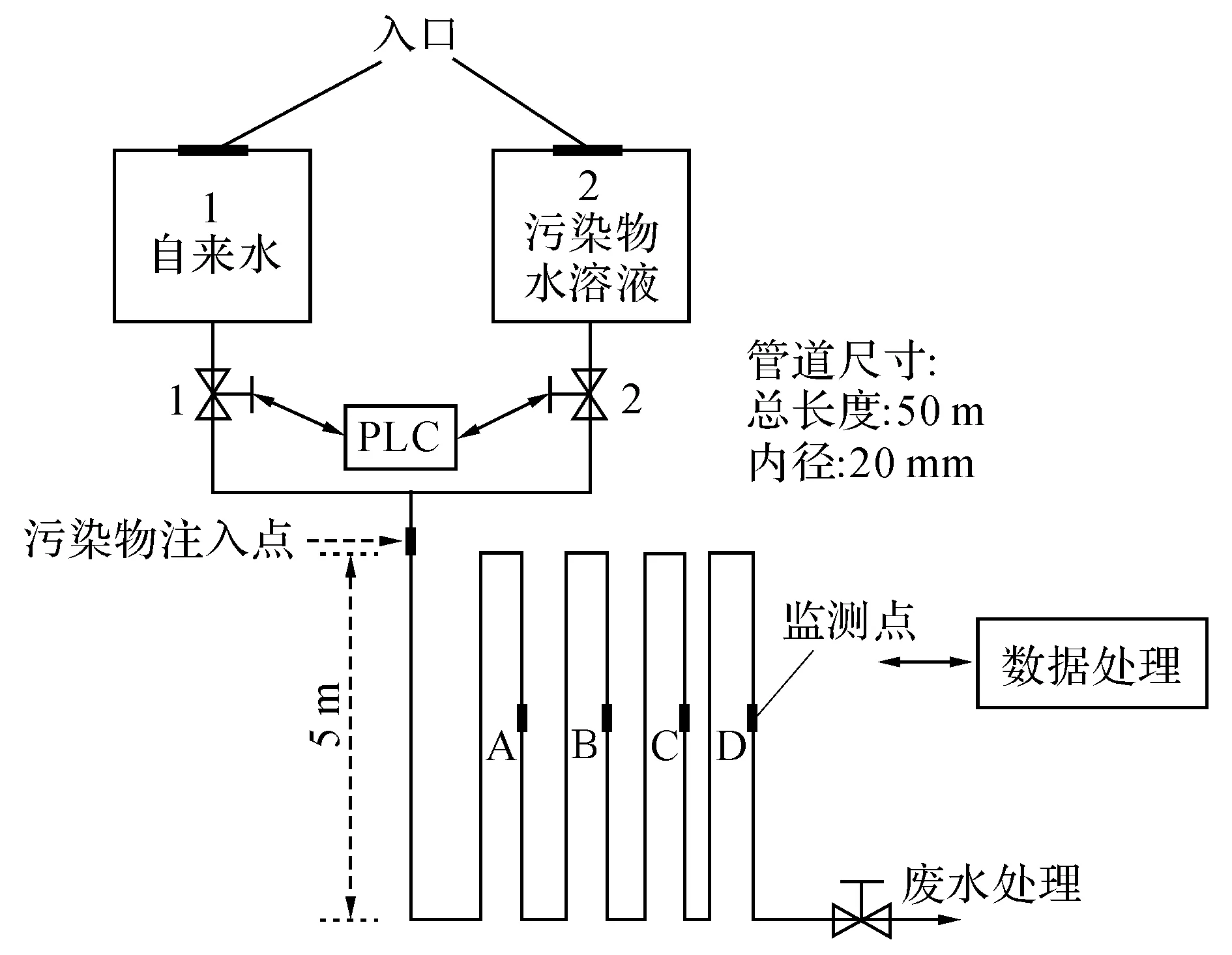
图3　污染注入模拟实验管网示意图Fig.3　Experimental pipeline system structure diagram

根据《生活饮用水卫生标准》(GB5749-2006)的有关规定可知,城市饮用水的主要监测指标可以分为感官性状与一般理化指标、微生物指标、毒理指标、消毒剂指标以及放射性指标.虽然近几年传感器技术的迅猛提升使得针对特定污染物的专用指标分析技术得到了快速的发展,然而整个自然界污染物质种类繁多,专用指标分析技术很难覆盖全部种类.最常用的是诸如温度、浊度、pH、电导率等感官性状与一般理化指标.在该实验系统中,进行在线测量的水质指标包括pH、浊度(turb)、溶解氧(dissolvedoxygen,DO)、总有机碳(totalorganiccarbon,TOC)、化学需氧量(chemicaloxygendemand,COD)、氨氮(NH3-N)、硝氮(NO3-N)和余氯(Cl),具体检测内容及测量精度如表1所示.表中，TD为浊度.所有传感器的采样间隔统一设置为1min.实验药品选用硫酸铜溶液和铁氰化钾溶液.这两种物质是电镀、制铜、颜料、制革等领域中常用的工业原料,也是《污水综合排放指标》和饮用水卫生标准中严控的指标,且这两类污染物一旦注入供水管网,将会引起多种常规水质监测指标的异常波动.

实验分为正常情况下的水质监测和污染物注入后的水质监测两个阶段,全部实验持续5h,包含301个采样时间点.前100min为正常情况下的水质监测实验,该过程开启主管路,关闭加药支路,通过在线监测仪器对各个水质参数进行在线测量.随后开展6组污染物注入实验,分别通过加药桶注入3组不同浓度的硫酸铜溶液和3组不同质量浓度的铁氰化钾溶液,具体加入的污染物溶液质量浓度如表2所示,每组注入实验持续时间为10min.表中，ρ1～ρ3分别为第1～3次注入质量浓度.

表1　污染注入模拟实验仪器仪表信息与对应检测项目

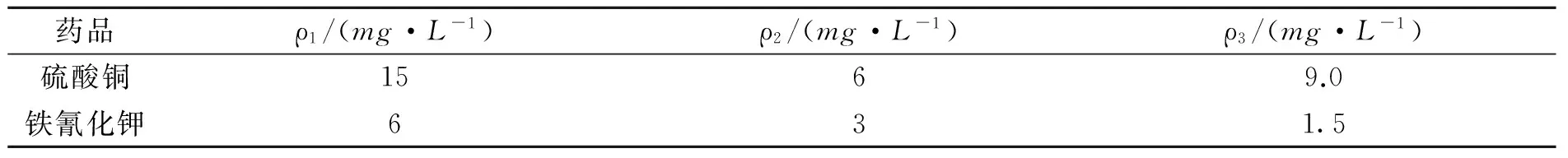
表2　污染注入模拟实验加药质量浓度

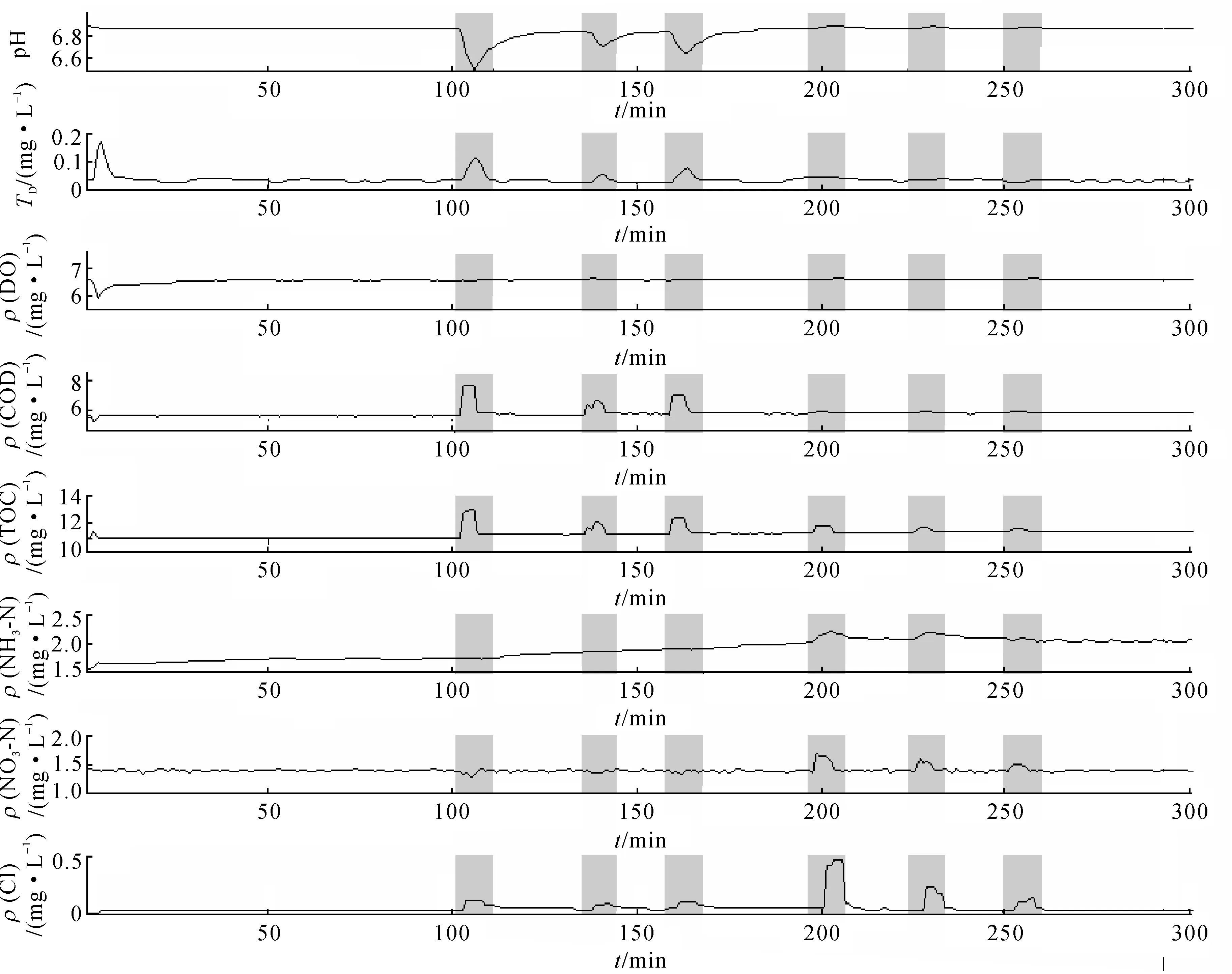
图4　正常的水质监测和污染物引起的异常Fig.4　Fluctuation in normal observation and contamination injection

图4记录的是正常情况下的水质波动和污染物注入后引起异常的监测结果.图中,t为时间.其中前100个点为正常水质的监测结果,用于训练窗口短时均方根和两两参数间动态距离的平均值.从第101点开始出现的灰色阴影部分表示污染物添加时刻.前3个灰色阴影分别对应于三次硫酸铜溶液注入,后3个分别对应铁氰化钾溶液的注入.

2.2单参数的基本异常概率计算

利用前100min系统正常运行情况下的水质监测数据,分别计算出8个参数历史情况下短时均方根的均值σ.从第101个时间点开始进行污染物注入实验,通过比较各参数在当前窗口内的短时均方根D与历史均值σ的偏离程度来计算单参数的基本异常概率.分别选取硫酸铜注入实验中t1=105时刻和铁氰化钾注入实验中t2=205时刻的监测值进行分析,得到各参数的基本异常概率Pab,如表3所示.

表3　单参数基本异常概率计算

由基本异常概率可以看出,在硫酸铜溶液注入实验中,pH、COD、TOC反应强烈,氨氮、硝氮、余氯反应不明显；在铁氰化钾溶液注入实验中,TOC、氨氮、硝氮、余氯反应强烈,pH、浊度没有明显变化.若基于单一参数的检测结果进行异常判断,则非常容易产生漏报.接下来考虑引入多参数间的关联分析.

2.3多参数的动态关联矩阵计算

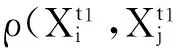
图5　正常情况下各参数的平均动态距离矩阵Fig.5　Average dynamic distance matrix under normal observation

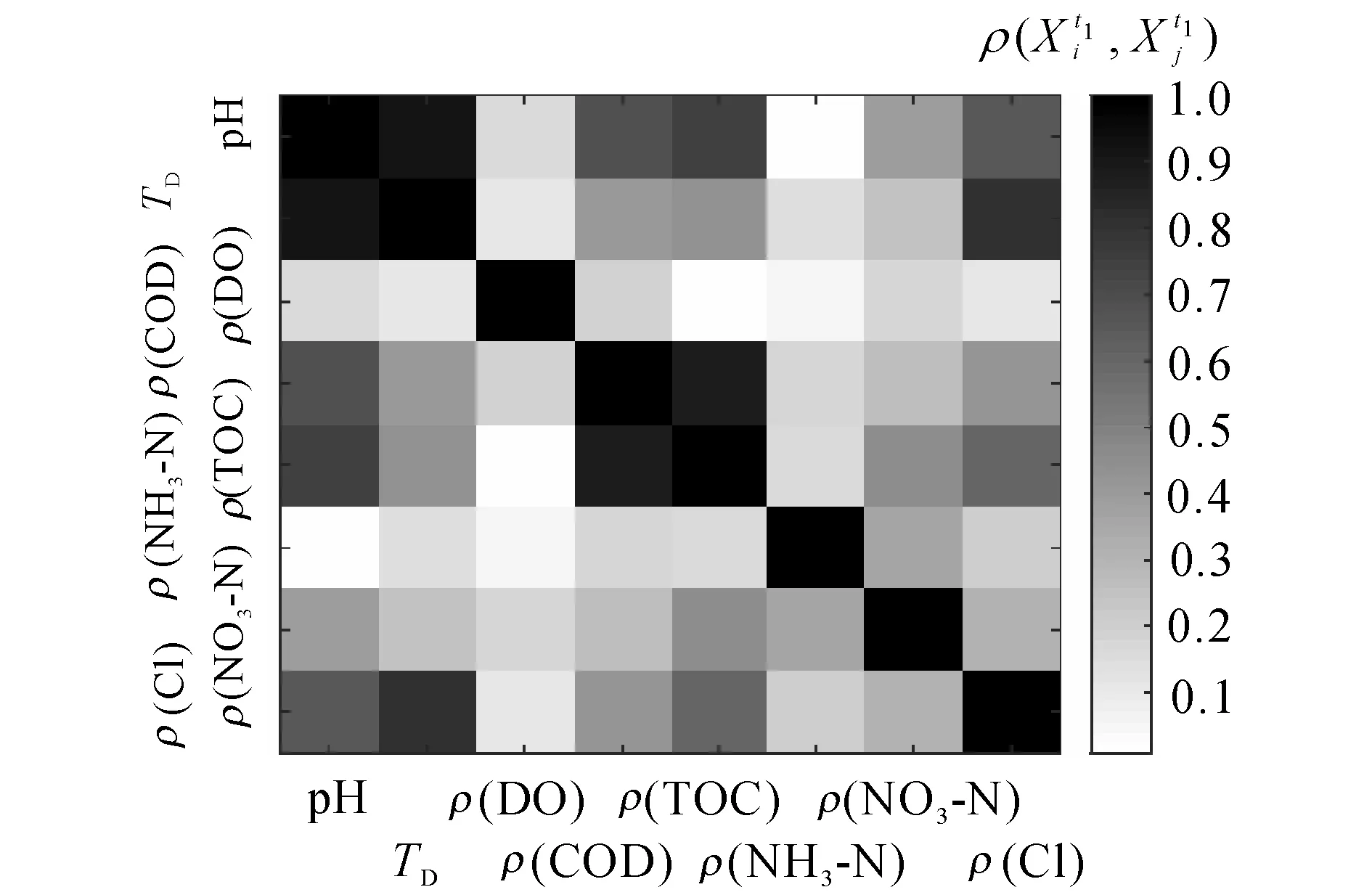
图6　t1=105时刻多指标动态关联程度示意图Fig.6　Multi-parameters dynamic correlation diagram at t1=105

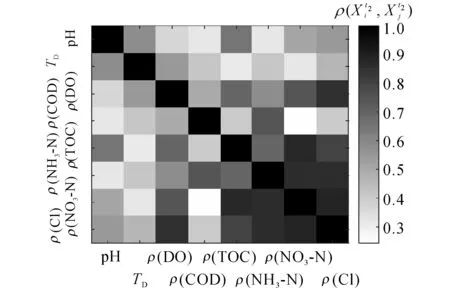
图7　t2=205时刻多指标动态关联程度示意图Fig.7　Multi-parameters dynamic correlation diagram at t2=205

2.4概率合成与异常判断

利用提出的合成规则,将单指标的基本异常概率和多指标的关联系数进行相乘,并从中选取最大值,可以得到t1=105和t2=205两个时刻融合后的异常概率分别为

P(t1)=0.670 3,P(t2)=0.764 9.

(8)

得到融合的概率后,通过与设定的阈值进行比较,可以作出异常判断.

3实验结果分析

3.1检测结果统计分析

对各参数所有时刻的监测数据进行分析处理,将融合概率的异常判断结果按真阳性(truepositive,TP)、假阳性(falsepositive,FP)、真阴性(truenegative,TN)及假阴性(falsenegative,FN)进行统计,具体定义参见表4.根据统计的判定结果,可以定义算法的判断准确度(accuracy,ACC).

表4　异常检测混淆矩阵

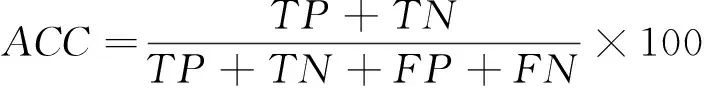
(9)

基于以上定义,记录301个采样点的判定结果,如表5所示.设置触发异常报警的概率阈值为0.65,得到融合后的检测结果,如图5所示.从实验的统计结果可以看出,6次污染事件都成功检出,检测准确度可达95.3%.

表5　水质检测统计结果

如表5所示,在整组实验的301个时间点中,共产生3个误报(FP)的时间点,其中有2个误报点是发生在整组实验开始的阶段.对比图4可以看出,由于系统刚刚启动,浊度、溶解氧等指标相对不稳定,造成误判.针对产生的11个漏报(FN)的时间点进行深入分析.图8中，AE、AR分别为实际情况和检测结果.由图8可以看出,这些漏报点都发生在事件开始的阶段,即在事件发生与产生报警之间存在一定的迟延,平均每次事件的迟延为1.0～2.0个时间步长.

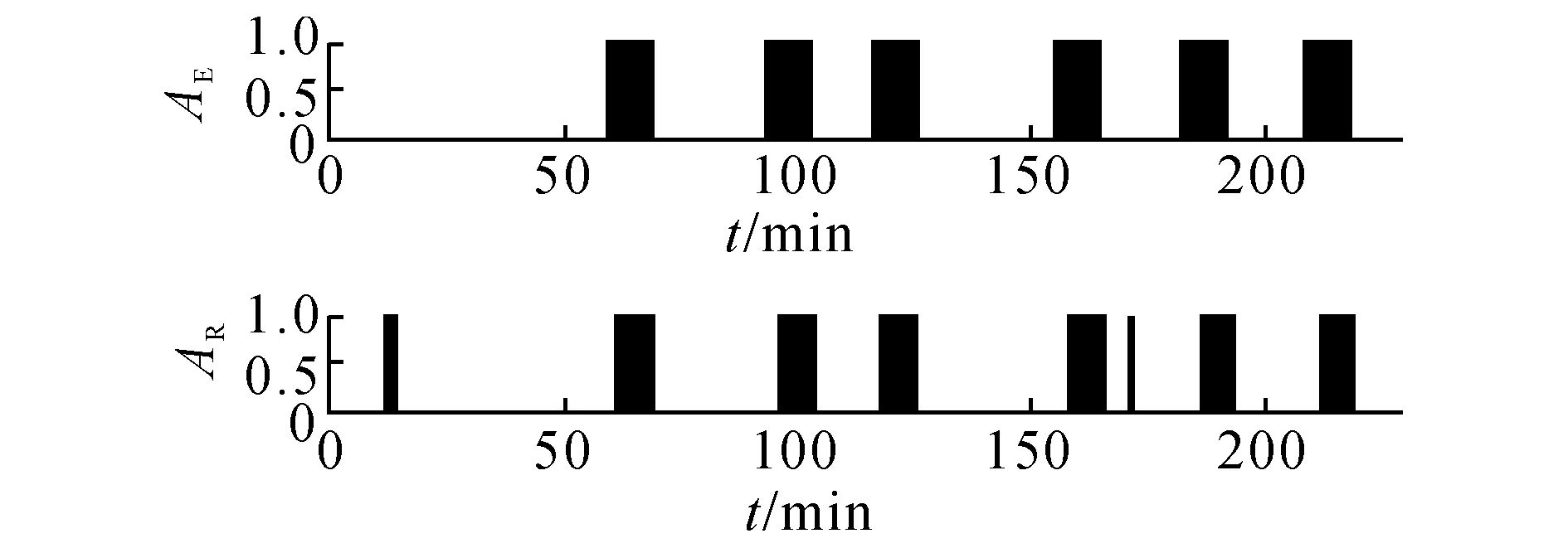
图8　实际事件与检测结果对比图Fig.8　Comparison between actual events and detection results

3.2ROC曲线和异常检测性能分析

ROC曲线[23](受试者工作特征曲线)是使用最广泛的算法性能评价方法.ROC曲线是以误报率(falsepositiverate,FPR)为横坐标、检出率(truepositiverate,TPR)为纵坐标绘制而成的,曲线与横轴和直线x=1所围成的图形面积被称为ROC曲线下面积.ROC曲线下面积越大,算法的性能越好.此外,从原点引出的对角线意味着随机判定的结果,因此一个算法的ROC曲线应在对角线左上方,才能说明该方法是有效的.

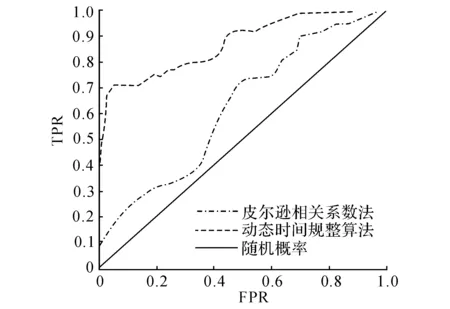
图9　ROC曲线效果图Fig.9　Roc curve comparison diagram

如图9的虚线所示为采用动态时间规整算法得到的ROC曲线.为了凸显动态时间规整在处理时间轴存在形变问题时的有效性,引入直接利用皮尔逊相关系数法(具体算法参见文献[16])计算两两指标之间的波动相关性的方法进行对比,ROC曲线如点划线所示.从图9可以看出,虽然皮尔逊相关系数法相较于其他的多指标融合水质异常检测算法而言,将多个参数之间的相关性纳入水质评价当中,但由于受各参数在时间轴上表现不一致的影响,ROC曲线下面积明显小于基于动态时间规整算法的ROC曲线下面积.特别是当误报率较小时,动态时间规整算法的检出率远高于相关系数法.这说明基于动态时间规整的异常检测算法不仅能够较好地挖掘各参数之间的波动相关性,更避免了因参数反应速度不一致所带来的影响,具有较好的检测效果.

4结语

针对目前城市供水水质污染种类众多、现有报警技术未充分利用多指标内在关联信息等问题,本文提出基于多水质指标间动态关联分析进行水质异常检测的方法.通过衡量单参数层面的异常概率以及多参数两两之间的动态相关性,得到融合后的水质异常概率,从而判断当前水质是否存在异常.选取多组不同浓度的硫酸铜溶液和铁氰化钾溶液进行管网模拟实验,利用实验所得的数据对方法的有效性进行验证.实验结果表明,采用该方法可以有效地挖掘污染物注入前、后水质指标间的内在联系,利用关联信息对因污染物引起的水质异常波动进行检测和识别,在保证了检出率的情况下尽可能降低误报率,同时能够较好地克服各参数在时间轴上表现不一致所带来的干扰,实现更加及时、准确地水质异常检测.城市供水管网的空间跨度远大于实验室模拟系统,因此在实际应用中,算法的性能可能会受制于传感器安装位置以及响应速度的影响.未来的研究可以着眼于如何利用供水网络中多个检测站点的信息来提升异常检测的准确性.

参考文献(References)：

[1]TAMMINENS,RAMOSH,COVASD.WatersupplysystemperformancefordifferentpipematerialspartI;waterqualityanalysis[J].WaterResourcesManagement, 2008, 22(11): 1579-1607.

[2]BYERMD,CARLSONK.Real-timedetectionofintentionalchemicalcontaminationinthedistributionsystem[J].JournalAmericanWaterWorksAssociation, 2005, 97(7): 1-34．

[3]FARUKD.AhybridneuralnetworkandARIMAmodelforwaterqualitytimeseriesprediction[J].EngineeringApplicationsofArtificialIntelligence, 2010, 23(4): 586-594．

[4]BABINSM,BURKOMHS,MNATSAKANYANZR,etal.Drinkingwatersecurityandpublichealthdiseaseoutbreaksurveillance[J].JohnsHopkinsAplTechnicalDigest, 2008, 27(4): 403-411．

[5]OLIKERN,OSTAFELDA.Acoupledclassification-evolutionaryoptimizationmodelforcontaminationeventdetectioninwaterdistributionsystems[J].WaterResearch, 2014, 51(6): 234-245．

[6]PERELMANL,ARADJ,HOUSHM,etal.Eventdetectioninwaterdistributionsystemsfrommultivariatewaterqualitytimeseries[J].EnvironmentalScienceandTechnology, 2012, 46(15): 8212-8219．

[7]MODARESIF,ARAGHINEJADS.Acomparativeassessmentofsupportvectormachines,probabilisticneuralnetworks,andk-nearestneighboralgorithmsforwaterqualityclassification[J].WaterResourcesManagement, 2014, 28(12): 4095-4111．

[8]ZOUH,ZOUZ,WANGX.AnenhancedK-meansalgorithmforwaterqualityanalysisoftheHaiheriverinChina[J].InternationalJournalofEnvironmentalResearchandPublicHealth, 2015, 12(11): 14400-14413．

[9]MCKENNASA,VUGRINED,HARTDB,etal.Multivariatetrajectoryclusteringforfalsepositivereductioninonlineeventdetection[J].JournalofWaterResourcesPlanningandManagement, 2013, 139(1): 3-12．

[10]OLIKERN,OSTFELDA.Minimumvolumeellipsoidclassificationmodelforcontaminationeventdetectioninwaterdistributionsystems[J].BulletinoftheAtomicScientists, 2014, 57(6): 1-12．

[11]MCKENNASA,KLISEKA.Multivariateapplicationsfordetectinganomalouswaterquality[C] ∥ 2006WaterDistributionSystemsAnalysisSymposium.Cincinnati: [s.n.], 2006: 1-11．

[12]YANGYJ,HAUGHTRC,GOODRICHJA.Real-timecontaminantdetectionandclassificationinadrinkingwaterpipeusingconventionalwaterqualitysensors:techniquesandexperimentalresults[J].JournalofEnvironmentalManagement, 2009, 90(8): 2494-2506．

[13]OLIKERN,OSTFELDA.Waterqualityeventdetectioninwaternetworksthroughmultiplesensorsdata[C] ∥ProceedingsofWorldEnvironmentalandWaterResourcesCongress.Austin:IEEE, 2015: 902-906．

[14]BENSALEHMS,QASIMSM,OBEIDAM,etal.Areviewonwirelesssensornetworkforwaterpipelinemonitoringapplications[C] ∥ 2013CollaborationTechnologiesandSystems(CTS)ofIEEE.SanDiego:IEEE, 2013: 128-131．

[15]JONATHANA,MASHORH,LINAP,etal.Adynamicthresholdsschemeforcontaminanteventdetectioninwaterdistributionsystems[J].WaterResearch, 2013, 47(5): 1899-1908．

[16]SHUMINGL,HANC,KATES,etal.Contaminationeventdetectionusingmultipletypesofconventionalwaterqualitysensorsinsourcewater[J].EnvironmentalMonitoringandAssessment, 2014, 16(8): 2028-2038．

[17]MUNIZCD,NIETOPJ,FERNANDEZJR,etal.DetectionofoutliersinwaterqualitymonitoringsamplesusingfunctionaldataanalysisinSanEstebanestuary(NorthernSpain) [J].ScienceoftheTotalEnvironment, 2012, 439(1): 54-61．

[18]GIAOBC,ANHDT.Similaritysearchinmultiplehighspeedtimeseriesstreamsunderdynamictimewarping[C] ∥ 2015NationalFoundationforScienceandTechnologyDevelopmentConferenceonInformationandComputerScience.HoChiMinhCity:IEEE, 2015: 82-87．

[19]ZHUQY,ZHANGGX,FENGTH,etal.Studyonwaterqualityanalysisandearly-warningtechnologybasedonroughsetandevidencetheory[J].JournalofZhejiangUniversity, 2012, 38(6): 747-754.

[20] 杨将新,郑华文,曹衍龙,等. 基于自适应AR模型的核电站松动件报警方法[J]. 原子能科学技术, 2010, 44(6): 701-705．

YANGJiang-xin,ZHENGHua-wen,CAOYan-long,etal.Alarmingmethodofloosepartsinnuclearpowerplantbasedonadaptiveauto-regressivemodel[J].AtomicEnergyScienceandTechnology, 2010, 44(6): 701-705．

[21] 李正欣,张凤鸣,李克武. 基于DTW的多元时间序列模式匹配方法[J]. 模式识别与人工智能, 2011, 03(4): 425-430．

LIZheng-xin,ZHANGFeng-ming,LIKe-wu.DTWbasedpatternmatchingmethodformultivariatetimeseries[J].PatternRecognitionandArtificialIntelligence, 2011, 03(4): 425-430．

[22]BERNDTDJ,CLIFFORDJ.Findingpatternsintimeseries:adynamicprogrammingapproach[J].AdvancesinKnowledgeDiscoveryandDataMining, 1996, 1(1): 229-248．

[23]FAWCETTT.AnintroductiontoROCanalysis[J].PatternRecognitionLetters, 2006, 27(8): 861-874.

收稿日期：2015-11-15.浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

基金项目：国家自然科学基金资助项目(61573313；U1509208)；浙江省科技厅公益资助项目(2014C33025)；浙江省重点研发计划资助项目(2015C03G2010034).

作者简介：魏媛(1990-)，女，硕士生，从事多源信息融合水质异常检测技术研究. ORCID: 0000-0002-5312-8791. E-mail: vera_wy@zju.edu.cn 通信联系人：黄平捷，男，副教授. ORCID: 0000-0002-5487-6097. E-mail: huangpingjie@zju.edu.cn

DOI:10.3785/j.issn.1008-973X.2016.07.025

中图分类号：X 832

文献标志码：A

文章编号：1008-973X(2016)07-1402-08

Contaminationeventdetectionmethodbasedondynamiccorrelationanalysisofmultiplewaterqualityparameters

WEIYuan,FENGTian-heng,HUANGPing-jie,HOUDi-bo,ZHANGGuang-xin

(State Key Laboratory of Industrial Control Technology, Zhejiang University, Hangzhou 310027, China)

Abstract:A multivariate correlation analysis method was proposed by exploring the internal correlation within conventional water quality parameters before and after the occurrence of contamination event in order to improve the performance of the existing water quality anomaly detection methods. The dynamic distance between each two monitored parameters was calculated to define the fluctuation correlation of the two time series by using the dynamic time warping (DTW) method. The correlation coefficient was fused with univariate basic abnormal probability based on D-S evidence theory in order to obtain the fused probability. The synthesis alarm decision was made by comparing the fused probability with the threshold. The proposed method was tested with experimental monitoring data collected from the laboratory pipeline system. Different concentrations of copper sulfate and potassium ferricyanide were separately injected into the pipeline system. Eight conventional monitoring parameters were measured by sensors installed along the pipeline. The collected monitoring data was applied to correlation analysis and probability fusion based on the proposed method. The ROC analysis was introduced to verify the performance and validity of the techniques．

Key words:conventional water parameter; data fusion; water quality event detection; time series analysis; dynamic time warping; correlation analysis