内孤立波对水平圆柱潜体作用力的计算

殷文明,郭海燕,吴凯锋,2,马　东

(1. 中国海洋大学 工程学院,山东 青岛 266100; 2. 海洋石油工程股份有限公司,天津 300461)



内孤立波对水平圆柱潜体作用力的计算

殷文明1,郭海燕1,吴凯锋1,2,马东1

(1. 中国海洋大学 工程学院,山东 青岛 266100; 2. 海洋石油工程股份有限公司,天津 300461)

摘要:针对内孤立波对潜体的载荷作用,分析受力特性并建立合适的载荷计算方法.基于文献资料,选取mKdV(modified KdV)理论,建立两层流体中考虑浮力变化的内孤立波对顺流向放置潜体的垂向力及力矩的计算方法,使用Matlab编制计算程序.利用已有文献试验结果对本文计算结果的可靠性进行验证,分析潜体所受垂向力及力矩在内波流场中不同位置处的时历变化.结果表明,下凹型内孤立波在上层流体中对潜体的垂向力及力矩大于在下层流体中对潜体的垂向力及力矩.垂向力在波谷前、后位置方向相反,具有垂向上、下剪切特性,在穿越过程中会对潜体产生强大的垂向力矩,尤其是在内界面与波面之间的流体层中,密度变化导致潜体产生浮力差.潜体所受的总垂向作用力及力矩远大于内孤立波本身对潜体的垂向作用力及力矩,分层流体中浮力的变化对潜体的影响至关重要.

关键词：mKdV理论；内孤立波；潜体；两层流体

内孤立波是发生在密度稳定层化的海水内部的非线性大振幅波动,最大振幅出现在海洋内部,是海洋中的一种普遍现象,其在传播过程中会产生突发性强流.Bole等[1]对流花油田的3个观测点进行研究,预测年最大内孤立波流速约为2 m/s ,10年一遇的最大内孤立波流速约为2.6 m/s,100年一遇的最大内孤立波流速约为3 m/s.Cai等[2-4]观测发现,从吕宋海峡到东沙群岛之间的海域所观测到的内孤立波强度较大,以向下凹陷波型为主,波致流速为1.5～2.9 m/s,最大振幅为170 m.内孤立波对石油钻井平台、海底石油管道以及潜体等造成严重威胁.研究内孤立波的生成、传播机理及其与海洋结构物的相互作用具有重要的理论意义和实用价值.

在密度分层海洋中,海洋内部流动的弛豫过程、陆坡区域产生的Lee波传播和潮流受地形作用等造成的潮流流线分裂等都能诱导产生内孤立波[5].内孤立波的稳定传播是非线性效应和频散效应动力学平衡的结果,可以用 KdV、eKdV、mKdV 和 MCC 等理论来描述[6-9].Cheng等[10-13]基于KdV理论对内孤立波作用在小尺度垂直圆柱型杆件上的水平载荷特性进行研究,徐肇廷等[14]对内周期波场中一端固定的垂直桩柱、两端固定的水平桩柱波阻进行实验研究,Guo等[15-16]研究内孤立波作用下顶张力立管的极值响应,付东明等[17-18]利用 CFD 对两层流体中内孤立波与潜艇的相互作用进行数值模拟.

在海洋工程结构物的构件中,圆柱体是一种常用的几何形状,除了常见的竖直圆柱体结构物外,还有诸如潜艇、深潜器的主体以及半潜平台的横撑等水平圆柱型结构.以上研究大都针对内孤立波对垂直圆柱体的水平作用力进行研究,对垂向作用力的研究很少,尤其是对水平圆柱体垂向作用力的研究更少.由于内孤立波的大振幅波动、较强的波致流速以及垂向剪切等特性,垂向作用力的影响不可忽视.本文针对已有的文献参数,选取mKdV理论,对内孤立波与水平圆柱潜体的相互作用进行理论分析,建立内孤立波对水平圆柱潜体垂向力和垂向力矩的计算方法以及考虑浮力变化的垂向力和垂向力矩计算方法.通过Matlab编写计算程序,对潜体位于上层流体、内界面以及下层流体三种情形进行作用力计算,研究垂向受力特性.对本文计算结果的可靠性进行验证,结果吻合较好.

1理论分析

1.1基于mKdV理论的波致流速度和加速度

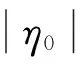
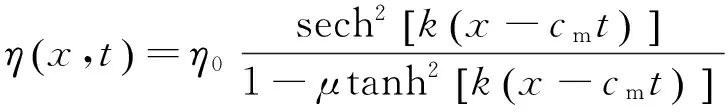
(1)

式中：

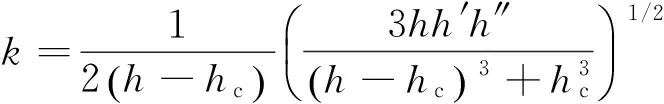
其中，

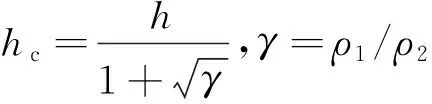
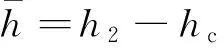
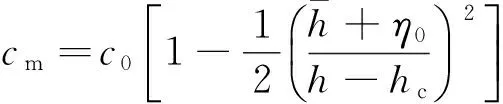
其中，

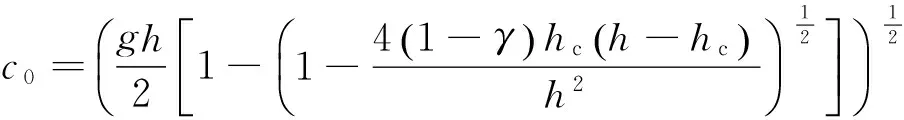
内孤立波为下凹型时η0取负值,上凸型时η0取正值.在两层流体中,内孤立波引起的水平速度和水平加速度分别记为Ui和U′i,其中i=1,2分别表示上、下层流体.由Osborne等[8]的研究可知,水平速度可以表示为

(2)

水平加速度U′i=∂Ui/∂t,记Δ=k(x-cmt),即

(3)

在上述理论公式的基础上,对垂向速度和垂向加速度进行推导,垂向速度和垂向加速度分别记为Wi和W′i.设各层流体均为不可压缩流体,则内孤立波引起的流速满足连续性方程为

(4)

可得垂向速度为

(5)

垂向加速度W′i=∂Wi/∂t,即

(6)

1.2内孤立波作用力计算方法

对于小直径构件主要采用莫林森方程,它主要用于垂直桩柱的水平作用力计算,但从流场角度分析可知,对水平桩柱的垂向力计算同样适用.

1.2.1内孤立波垂向力及力矩莫里森方程是一个半经验半理论方法,它认为当结构物直径D与波长λ相比很小(D/λ≤0.15)时,可以忽略该结构物对流场的影响.此时,结构物所受的波浪力可以视为由两部分组成：1)由未受扰动的流场所产生的速度力；2)由流体加速度场产生的惯性力,方程[19]如下：

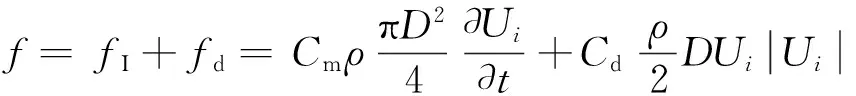
(7)

式中：fI为惯性力项；fd为速度力项；Cm和Cd分别为惯性力系数和速度力系数,其中Cm=1+Ca,Ca为附加质量系数；ρ为海水的平均密度；Ui取结构物轴心处原流场水质点速度；D为结构物直径.

设顺流向放置水平圆柱体的长度为L,如图1所示,由式(5)～(7)可得,所受的内孤立波垂向力可以表示为

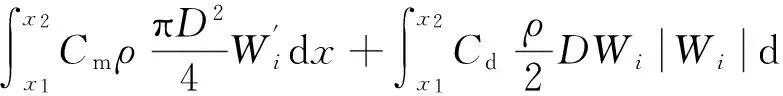
(8)

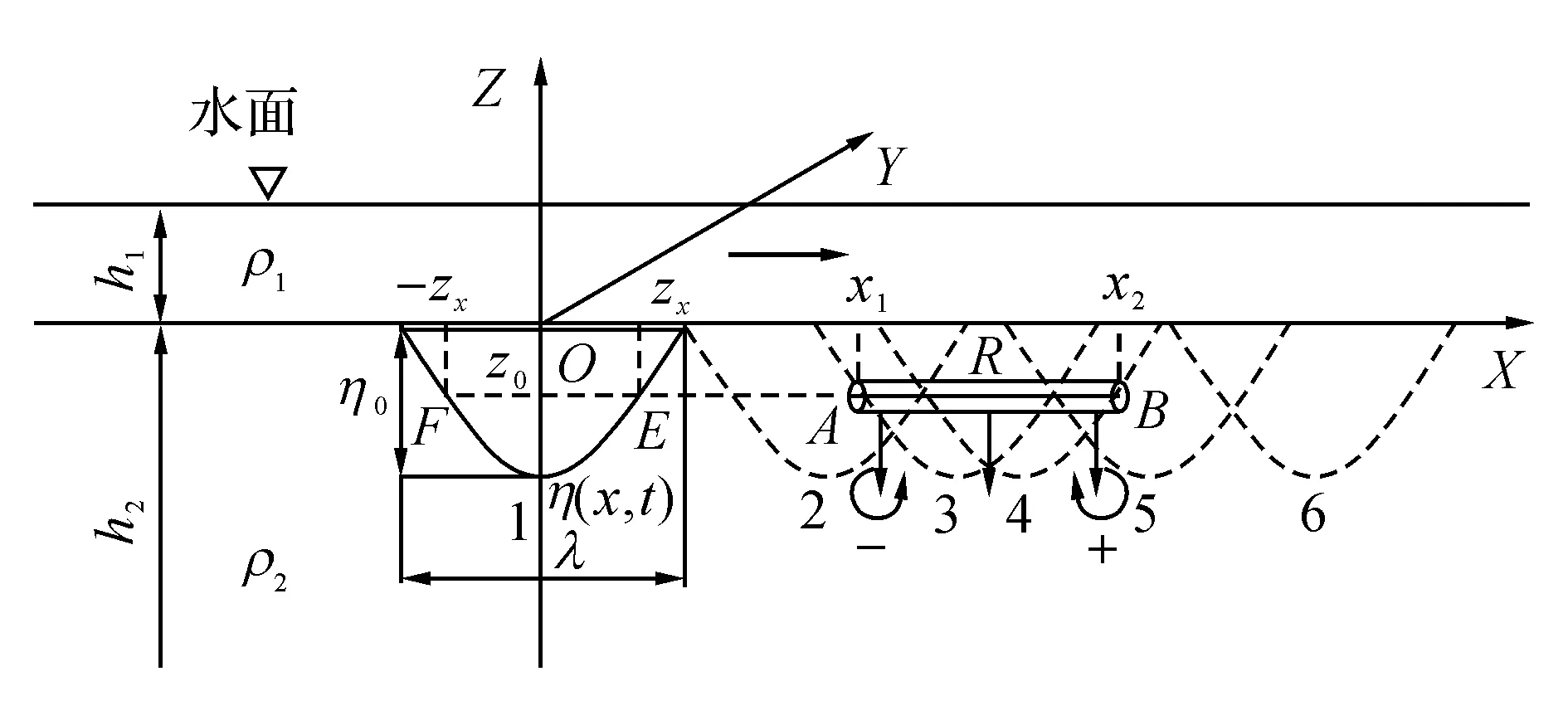
图1　内孤立波与水平圆柱体作用示意图Fig.1　Schematic of horizontal cylinder under internal solitary wave

式中：x2-x1=L,Wi和W′i分别取圆柱体轴线位置任意长度处波浪水质点的垂向速度和垂向加速度.

取圆柱体的中心为重心R,对R求力矩并取逆时针旋转为负.分析图1可知：在R的左边位置,力与力矩同号；在R的右边位置,力与力矩异号.内孤立波垂向力矩可以表示为

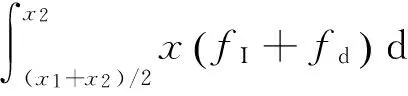
(9)

1.2.2考虑浮力变化的内孤立波垂向力及力矩当内孤立波穿越圆柱体时,上、下层流体的密度差会导致圆柱体浮力产生变化,使圆柱体受到一个向下的作用力.

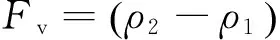
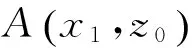
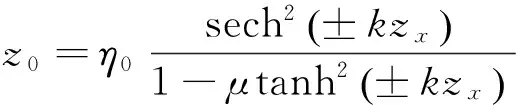
(10)

图1中,数字1～6表示内孤立波穿越圆柱体的6个不同时刻,分别如下：1为初始时刻,2为内孤立波右半弧穿越圆柱体左半轴,3为内孤立波右半弧穿入圆柱体右半轴,4为内孤立波左半弧穿入圆柱体左半轴,5为内孤立波左半弧穿入圆柱体右半轴,6为内孤立波穿出圆柱体.由mKdV理论可知,内孤立波波形传播速度为cm.分析6个不同时刻圆柱体位于上层流体中的体积,可得V1的近似表达式：

V1=

(11)

由式(8)、(11)可得,圆柱体所受的垂向力为

f′v=fv-Fv=

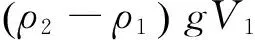
(12)

由式(9)、(12)可得,圆柱体所受的垂向力矩为

M′v=

(13)

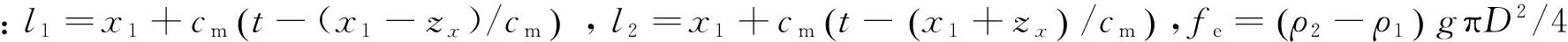
1.3内孤立波作用力计算程序

基于以上理论的分析,利用Matlab编写了相应的计算程序,如下所示.

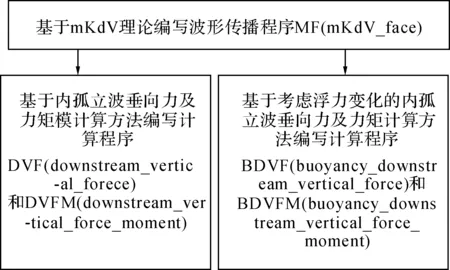
2算例分析

2.1内孤立波及潜体参数

采用文献[17]的算例参数,上、下层流体密度分别为ρ1=998 kg/m3和ρ2=1 024 kg/m3,上、下层流体深度分别为h1=100 m和h2=200 m.内孤立波高为40 m,由于上层深度小于下层深度,故为下凹型内孤立波,则η0=-40 m.由黄文昊等[20]关于有限深两层流体中内孤立波造波实验可知,当内孤立波振幅接近mKdV理论的极限振幅时,该理论是适用的.基于该算例参数下的mKdV理论解的极限振幅[20]为

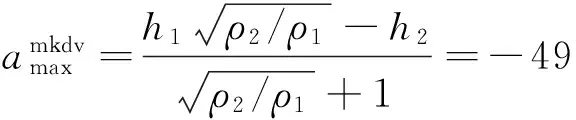
付东明等[17]采用经放大20倍后的suboff主体作为潜体模型,总长度为87.118 m,最大回转半径为5.080 m.本文在模型的处理上,将潜体简化为等长度的圆柱型结构,左侧位于ox轴正向2 250 m处.内孤立波的特征宽度λ通常定义为大于等于振幅5%的那部分波形的宽度,本文中λ=2 949m,可以采用莫里森方程进行潜体的受力分析.由文献[19,21]可知,一般工程中,圆柱体的附加质量系数取1,速度力系数与雷诺数Re有关.稳定流时,在亚临界区(水流呈层流状态),Re<2.0×105,Cd约为常数,可以取为1.2；在临界区,Re=2.0×105～5.0×105,该区域内阻力系数迅速下降；在超临界区,柱体后形成强烈漩涡,Re>5.0×105,Cd大体稳定,可取0.60～0.70.由式(2)、(5)可知,水平速度和垂向速度的最大值分别为1.73和0.23 m/s,对应的雷诺数分别为1.76×107和2.37×106,本文中Cm和Cd分别取2.0和0.7.

2.2CFD数值试验的验证

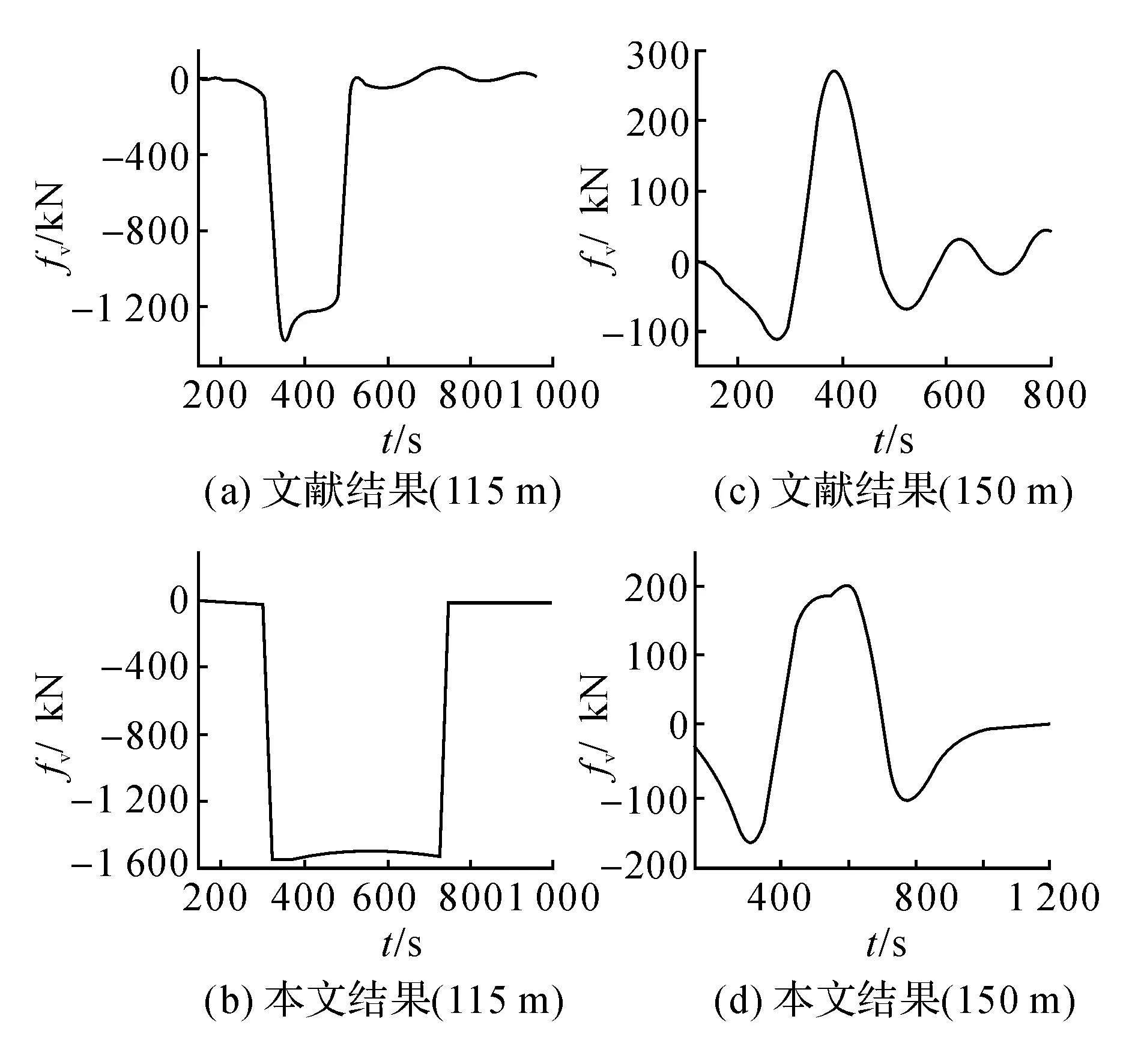
图2　潜体在内界面与波面之间流体以及下层流体中所受垂向力时间历程对比Fig.2　Comparison of time histories of exciting forces on submerged body in middle and lower layer

付东明等[17]研究了潜体位于内界面和下层流体中的垂向力时历变化,将CFD数值试验结果与本文的计算结果汇成图2进行比较,验证本文计算程序的可行性.本文对文献[17]中潜体模型的简化处理会造成定量研究上的差别,但不会影响定性研究.对比图2(a)、(b)可知,当潜体位于内界面与波面之间的流体层(水下115 m)时,本文给出的垂向力变化趋势与文献[17]的结果基本一致,但两次突变的时间间隔大于文献结果,垂向力略大于文献结果；对比图2(c)、(d)可知,当潜体位于波面下层(水下150 m)时,本文与文献[17]的受力时历曲线变化趋势基本一致,但是本文结果略小于文献结果.本文是基于理论研究建立的计算方法,均不会产生数值造波中尾波列的情形[17],因此曲线的后续变化趋于平缓而非波动.

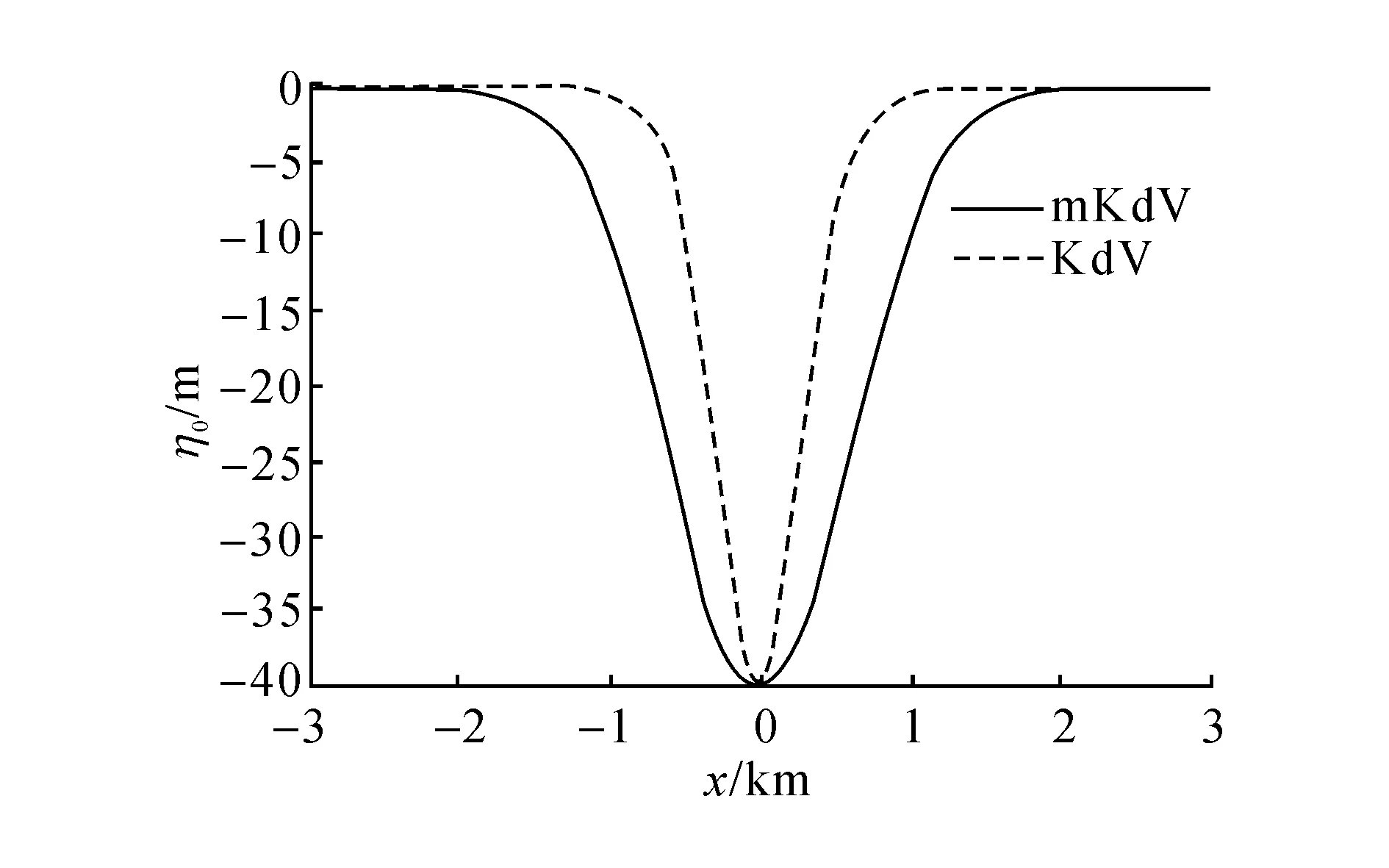
图3　KdV与mKdV波面对比图Fig.3　Comparison of wave face of KdV and mKdV

本文是基于mKdV理论下建立的流场,而文献[17]中的数值造波是将KdV理论下得到的上、下层流体速度作为上、下推板的运动速度,以此实现的双推板数值水槽造波,产生的内孤立波波长更接近于KdV理论下的波长.将基于同一参数下两种理论产生的内孤立波波面对比图汇成图3.可知,mKdV理论下的波长更长,在传播速度相近的情况下,穿越潜体的时间历程更长久,因此导致曲线幅值变化的时间间隔大于文献[17]的结果.

潜体模型的简化处理以及拖曳力系数和惯性力系数的选取等因素会造成本文结果与文献[17]结果在定量上的差别.由黄文昊等[20]给出的mKdV理论的适用性条件可知,在上、下层流体深度不接近临界值的情况下,当内孤立波振幅接近mKdV理论的极限振幅时,该理论是适用的.本文采用mKdV理论进行分析计算具有合理性.

2.3潜体受力分析

考虑3种潜体下潜深度：1)潜体放置于两层流体分界面处,即水下100 m处：2)潜体放置于水下115 m处,正好穿过内孤立波；3)潜体放置于水下150 m处,潜体位于整个孤立波的下方.内孤立波从左向右沿ox轴正向传播,如图1所示.

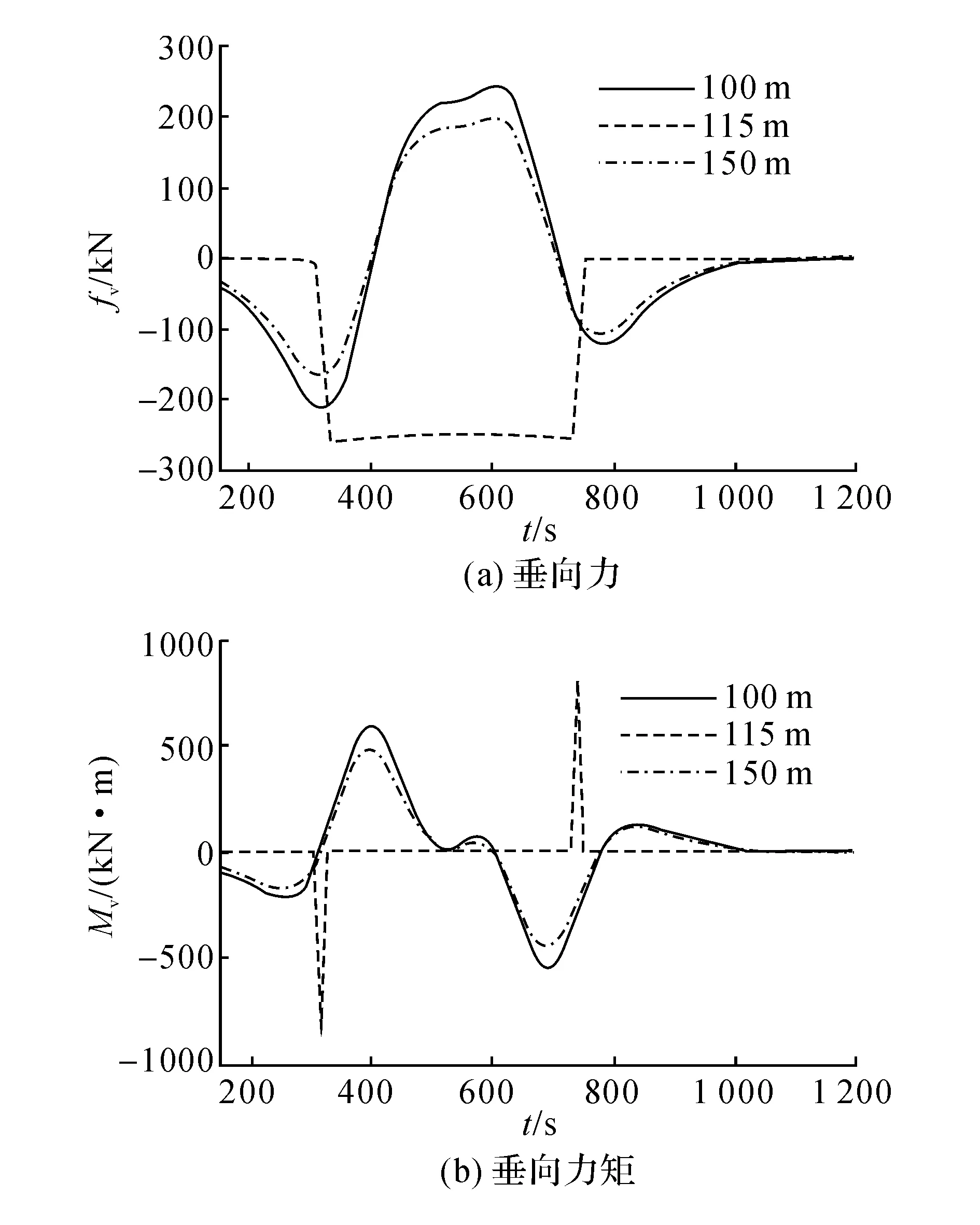
图4　潜体在上、下层流体以及内界面与波面之间流体中受力的时间历程Fig.4　Time histories of exciting forces on submerged body in upper, middle and lower layer

基于上述编写的计算程序,结合算例参数,计算以上3种深度处潜体在内孤立波作用下所受的垂向力以及垂向力矩,如图4所示.其中,图4(a)中标注115 m的曲线比实际值缩小了6倍,图4(b)中标注115 m的曲线比实际值缩小了20倍.

从整体受力角度分析,由图4(a)可知,内孤立波对潜体的垂向作用力在上层和下层有着相同的时间变化趋势,但上层流体中的垂向力明显大于下层；在内界面与波面之间的流体层中产生的垂向力远大于上下层流体中的垂向力,垂向力的幅值最大相差6倍,导致该差值的原因在于：在内孤立波穿越潜体的过程中,会使潜体的前、后两端位于不同密度的流体层中,因此产生浮力差.由此可见,在内孤立波穿越潜体的过程中,浮力的影响至关重要.

由图4(b)可知,在上层流体中所受的垂向力矩大于在下层所受的垂向力矩,并且方向保持一致.当潜体位于内界面与波面之间的流体层时,当内孤立波穿入和穿出潜体时垂向力矩急剧增大,此时远大于在上层和下层所受的垂向力矩,这种由浮力引起的急剧变化的强大力矩极有可能导致潜体瞬间产生破损、失稳甚至倾覆.

从时间历程角度分析,由图4(a)可知,当第一次出现负向幅值时,内孤立波的波谷位置传至潜体前端,之后负向垂向力开始变小,直到波谷位置传至潜体中心,此时潜体垂向力变为零,之后垂向力转向变为正.由此可见,在波谷前、后位置垂向力方向相反,对潜体产生垂向剪切的作用力.

由图4(b)可知,在潜体放置于水下115 m处的情况下,当内孤立波传至潜体前端时,潜体所受的垂向力矩急剧增大,此时是浮力变小导致；当潜体完全浸入内孤立波中时,浮力产生的垂向力矩消失,但是浮力减小会导致悬浮状态的潜体下沉或者固定水平圆柱结构的自身承重力加大,直至内孤立波穿出潜体时,再次出现垂向力矩急剧增大的现象,但前、后两次方向相反.

3结论

(1)在下凹型内孤立波的传播过程中,在上层流体中潜体所受的垂向力及力矩大于在下层流体中的垂向力及力矩,并保持同向.

(2)当内孤立波波谷位置传至潜体时,内孤立波对潜体的垂向力在波谷前、后位置方向相反,具有垂向上、下剪切特性.

(3)在内孤立波穿越潜体的过程中,内孤立波波面上、下两层流体的密度差导致潜体的垂向力急剧增加和减小.此时浮力的影响远大于内孤立波本身对潜体产生的作用力,并产生强大的垂向力矩,使潜体失稳或者因遭受过重载荷而发生破损.

参考文献(References):

[1] BOLE J B, EBBESMEYER C C, ROMEA R D. Soliton currents in the South China Sea: measurements and theoretical modeling [C]∥ Proceedings of the 26th Annual Offshore Technology Conference. Houston: [s.n.], 1994: 387-396．

[2] CAI Shu-qun, GAN Zi-jun, LONG Xiao-min. Some characteristics and evolution of the internal soliton in the northern South China Sea [J]. Chinese Science Bulletin, 2002, 47(1): 21-26.

[3] YANG Y J, TANG T Y, CHANG M H, et al. Solitons northeast of Tung-Sha Island during the ASIAEX pilot studies [J]. IEEE Journal of Oceanic Engineering, 2004, 29(4): 1182-1199．

[4] KLYMAK J M, PINKEL R, LIU C T, et al. Prototypical solitons in the South China Sea [J]. Geophysical Research Letters, 2006, 33(11): L11607.

[5] 方欣华,杜涛. 海洋内波基础和中国海内波[M]. 青岛：中国海洋大学出版社,2005: 105-111．

[6] MICHALLET H, BARTHELEMY E. Experimental study of interfacial solitary waves [J]. Journal of Fluid Mechanics, 1998, 366(01): 159-177．

[7] SEGUR H, HAMMACK J L. Soliton models of long internal waves [J]. Journal of Fluid Mechanics, 1982, 118(118): 285-304．[8] OSBORNE A R,BURCH T L. Internal solitons in the Andaman Sea [J]. Science, 1980, 208(4443): 451-460．

[9] CHOI W, CAMASSA R. Fully nonlinear internal waves in a two-fluid system [J]. Journal of Fluid Mechanics, 1999, 396(3): 1-36．

[10] CHENG You-liang, LI Jia-chun, AN Lian-suo, et al. The induced flow field by internal solitary wave and its action on cylindrical piles in the stratified ocean [C]∥ 4th International Conference on Fluid Mechanics. Dalian: [s.n.], 2004: 296-299．

[11] CAI Shu-qun, LONG Xiao-min, GAN Zi-jun. A method to estimate the forces exerted by internal solitons on cylinder piles [J]. Ocean Engineering, 2003, 30(5): 673-689．

[12] CAI Shu-qun, LONG Xiao-min, WANG Shen-gan. Force and torques exerted by internal solitions in shear flows on cylinder piles [J]. Applied Ocean Research, 2008, 30(1): 72-77．

[13] 沈国光, 叶春生. 内波孤立子的非波导载荷计算[J]. 天津大学学报, 2005, 38 (12): 1043-1050．

SHEN Guo-guang, YE Chun-sheng. Load calculation of solitary waves for non-wave-guide [J]. Journal of Tianjin University, 2005, 38 (12): 1043-1050．

[14] 徐肇廷,陈旭,吕宏民,等. 内波场中水平桩柱波阻的实验研究[J].中国海洋大学学报, 2007,37(1): 1-6．

XU Zhao-ting, CHEN Xu, LV Hong-min, et al. An experimental study of wave-resistance of a horizontal cylinder in internal waves [J]. Periodical of Ocean University of China, 2007,37(1): 1-6.

[15] GUO Hai-yan, ZHANG Li, LI Xiao-min, et al. Dynamic responses of top tensioned riser under combined excitation of internal solitary wave, surface wave and vessel motion [J]. Journal of Ocean University of China, 2013, 12(1): 6-12．

[16] 张莉,郭海燕,李效民. 南海内孤立波作用下顶张力立管极值响应研究[J]. 振动与冲击, 2013, 32(10): 100-117．

ZHANG Li, GUO Hai-yan, LI Xiao-min. Extreme response of top tensioned riser under internal solitary wave in South China Sea [J]. Journal of Vibration and Shock, 2013, 32(10): 100-117．[17] 付东明, 尤云祥, 李巍. 两层流体中内孤立波与潜体相互作用的数值模拟[J]. 海洋工程, 2009, 27(3): 38-44．

FU Dong-ming, YOU Yun-xiang, LI Wei. Numerical simulation of internal solitary waves with a submerged body in a two-layer fluid [J]. The Ocean Engineering, 2009, 27(3): 38-44．

[18] 陈杰, 尤云祥, 刘晓东, 等.内孤立波与有航速潜体相互作用数值模拟[J]. 水动力学研究与进展, 2010, 25(3): 343-351．

CHEN Jie, YOU Yun-xiang, LIU Xiao-dong, et al. Numerical simulation of interaction of internal solitary waves with a moving submarine [J]. Chinese Journal of Hydrodynamics, 2010, 25(3): 343-351．

[19] 李玉成,滕斌. 波浪对海上建筑物的作用[M]. 北京：海洋出版社,2002: 250-268．

[20] 黄文昊,尤云祥,王旭,等.有限深两层流体中内孤立波造波实验及其理论模型[J].物理学报,2013,62(8):084705．

HUANG Wen-hao, YOU Yun-xiang, WANG Xu, et al. Wave-making experiments and theoretical models for internal solitary waves in a two-layer fluid of finite depth [J]. Acta Physica Sinica, 2013, 62(8): 084705．

[21] 唐友刚,沈国光,刘利琴. 海洋工程结构动力学[M]. 天津：天津大学出版社,2008: 14-15．

收稿日期：2015-06-05.浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

基金项目：国家自然科学基金资助项目(51279187).

作者简介：殷文明(1988-),男, 博士生,从事内波流场数值模拟的研究. ORCID: 0000-0002-0475-0939. E-mail:wmyinouc@163.com 通信联系人：郭海燕, 女, 教授, 博导. ORCID: 0000-0002-3392-2234. E-mail:hyguo@ouc.edu.cn

DOI:10.3785/j.issn.1008-973X.2016.07.005

中图分类号：TV 131; TV 139

文献标志码：A

文章编号：1008-973X(2016)07-1252-06

Calculation of internal solitary wave force on horizontal submerged circular cylinder

YIN Wen-ming1, GUO Hai-yan1, WU Kai-feng1,2, MA Dong1

(1.DepartmentofEngineering,OceanUniversityofChina,Qingdao266100,China；2.OffshoreOilEngineeringLimitedCompany,Tianjin300461,China)

Abstract:A proper load calculation method was established to analyze the characteristics of internal solitary wave loads on the submerged body. MKdV (modified KdV) theory was chosen considering the changes of buoyancy based on the literature data in order to establish the calculation method of the vertical forces and torques of internal solitary waves on the submerged body which is in-line placed. The reliability of the calculation results was verified with the existing test data by means of programming with Matlab. Three different locations were considered where the submerged body to be placed: the upper layer, the middle layer and the lower layer. Then the time histories of the vertical forces and torques of the body in these different locations were analyzed. Results show that the vertical forces and torques caused by internal solitary wave in the lower layer are less than that in the upper layer. The vertical force is in opposite directions before and after the wave trough position, which shows vertical shear properties. The internal solitary wave can generate strong vertical torque on the submerged body in the process of crossing. Especially in the middle layer, density changes lead to the buoyancy difference and the total forces and torques are far greater than which were caused by internal solitary waves. The buoyancy change on the influence of the submerged body is fatal in the stratified two-layer fluid.

Key words:mKdV theory; internal solitary wave; submerged body; two-layer fluid