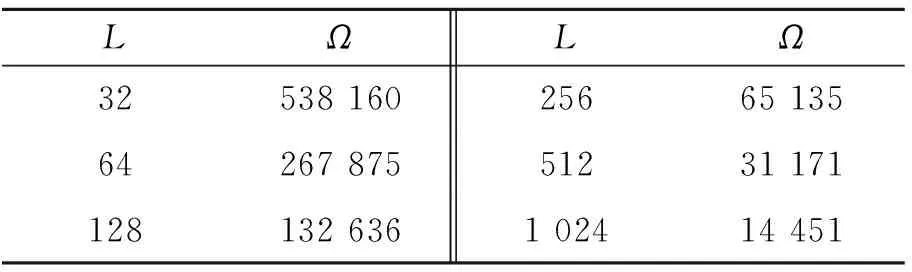
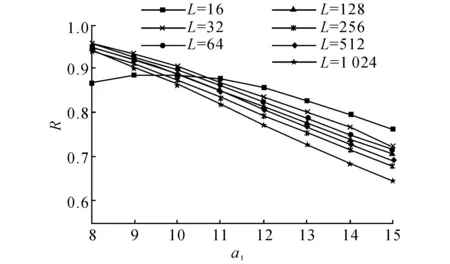
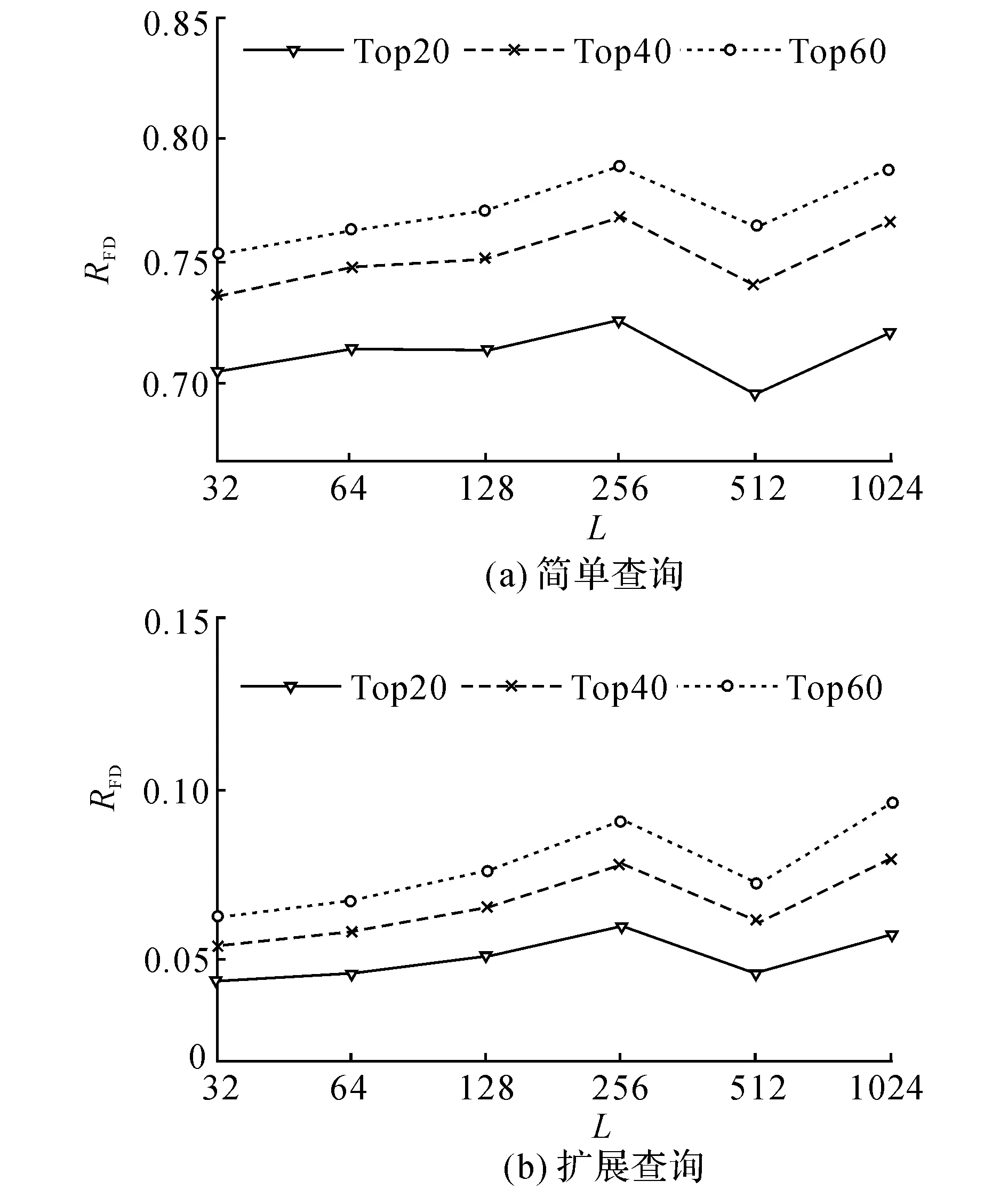
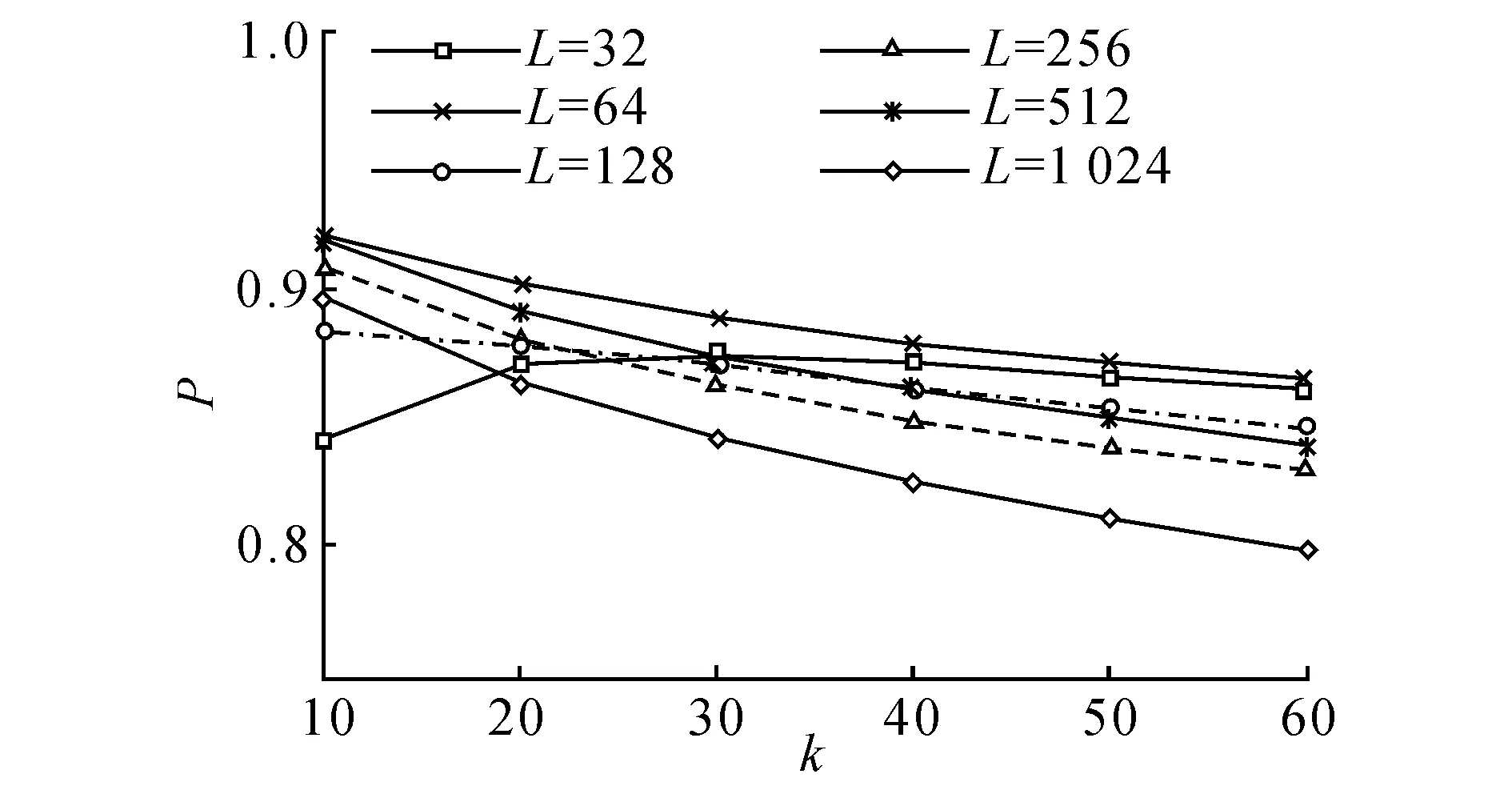
基于两级过滤的时间序列近似查询

蔡青林,陈　岭,梅寒蕾,孙建伶

(浙江大学 计算机科学与技术学院,浙江 杭州 310027)



基于两级过滤的时间序列近似查询

蔡青林,陈岭,梅寒蕾,孙建伶

(浙江大学 计算机科学与技术学院,浙江 杭州 310027)

摘要:针对现有的近似查询模型对查询精度的可控性较差,后续处理效率较低的问题,提出基于两级过滤的查询模型.通过采用不同粒度的SAX表示方法提取时间序列的字符型特征向量,可以将高维的时间序列映射到低维的特征空间；将不同粒度的特征向量以向量近似文件(VA-File)的结构进行存储,有效引入了倒排索引.在查询过程中,设计了启发式的查询过滤算法,根据粗粒度特征向量查询细粒度特征向量,实现第一级过滤；针对VA-File设计了高效的边界剪枝算法,实现第二级过滤.模型基于多粒度的SAX特征向量进行构建,可以对查询精度进行有效控制；在第二级过滤中采用的边界剪枝算法可以有效地提高后续处理的执行效率.实验结果表明,提出的查询模型具有较高的性能,对时间序列长度、kNN查询规模及数据集规模具有稳定的扩展性.

关键词：时间序列；相似性查询；符号聚集近似；向量近似文件；倒排索引

时间序列相似性查询是时间序列数据挖掘领域的基本问题,可简要描述为对于给定的一条时间序列,需要快速完整的从时间序列数据库中找出与其相似的序列.针对该问题,学术界提出了大量的查询模型[1],这些模型通常基于特定的数据表示方法,如奇异值分解(singular value decomposition, SVD)[2]、离散傅里叶变换(discrete fourior transformation, DFT)[3]、离散小波变换(discrete wavelet transformation, DWT)[4]、分段聚集近似(piecewise aggregation approximation, PAA)[5]、符号聚集近似(symbolic aggregation approximation, SAX)[6]等,将高维的时间序列映射到低维的特征空间,然后构建索引结构.模型的查询过程可以简要描述为：基于时间序列的近似表示查询索引结构获取候选集；通过磁盘I/O读取候选集的原始数据,并与查询序列进行精确比较,获得最终结果,该阶段称为后续处理[3].很明显,模型的查询效率由磁盘I/O的开销规模决定.

根据查询结果的完备性,模型可以分为精确查询模型与近似查询模型.对于前者,查询过程需要满足“下界定理”[7],即基于数据表示的度量距离须小于基于原始数据的度量距离,由此获得的候选集包含了所有的真实结果(即对原始数据通过线性扫描的查询结果).受下界定理的限制,精确查询模型的数据表示方法对原始数据的近似精度(或称下界紧凑度)较低,因此可能导致查询过程生成较大规模的候选集,影响模型的查询效率.为了满足实际应用对查询效率的高度需求,通过适当地牺牲查询结果的完备性来换取查询效率显著提升的近似查询模型,在近年来得到了广泛研究,比如最新提出的EBSM模型[8]、iSAX模型[9]、iSAX2.0模型[10]、最长相关子序列查询模型[11]等.尽管近似查询模型具有较高的查询效率,但是它们对查询精度的可控性较差,并且后续处理阶段的时间开销没有充分削减.

针对上述问题,基于多分辨率的SAX表示方法,提出基于两级过滤(two-step filtering)的时间序列近似查询模型.通过不同粒度的SAX表示提取时间序列的字符型特征向量,将高维的时间序列映射到低维的特征空间；将不同粒度的特征向量以向量近似文件(VA-File)的结构进行存储,并对其构建倒排索引.在查询过程中,设计了启发式的查询过滤算法,根据粗粒度特征向量查询细粒度特征向量,实现第一级过滤；针对VA-File设计了高效的边界剪枝算法,实现第二级过滤.由于模型基于多粒度的SAX特征向量构建倒排索引,查询过程可以对查询精度进行有效控制；在第二级过滤中所采用的边界剪枝算法可有效地提高后续处理的执行效率.

1相关工作

根据查询结果的完备性不同,时间序列相似性查询模型可以分为精确查询模型与近似查询模型.精确查询模型是目前研究较多且较成熟的方法,研究者们已经提出大量的时间序列数据表示方法及索引结构用于实现精确查询.比如,早期的DFT表示[3-7]通过提取时间序列的离散傅里叶系数作为特征,实现数据压缩,然后构建R*-树索引实现精确查询.该方法忽略了时间序列较多的局部特征,容易导致下界紧凑度较低.此后,基于分段表示和基于矩阵分解的方法相继被提出.常见的有PAA表示方法[5]和适应性分段常数 (adaptive piecewise constant approximation, APCA) 表示方法[12],它们分别将时间序列进行等长分段和适应性分段后,提取各子段的平均值特征来构建空间索引.基于简单的子段平均值的近似会导致较低的下界紧凑度.另外,还有分段线性表示方法(piecewise linear approximation, PLA)[13],提取子段的线性拟合斜率作为特征以及最新的导数分段近似(derivative segment approximation, DSA)[14],提取导数子序列的平均值作为特征.这两种方法都对噪声较敏感,容易受异常值的影响.常见的基于矩阵分解的表示方法有SVD[2]和主成分分析(principal component analysis, PCA)[15],但是这两类方法需要在内存中实现,使得它们的扩展性较差.

为了提高查询效率,近似查询模型正受到越来越多的研究.最新的EBSM模型[8]可以在查询精度损失较小的情况下,实现基于动态时间弯曲距离(dynamic time warping, DTW)的高效子序列匹配,但是没有考虑数据规范化问题[16],所以查询结果无意义.最长相关子序列查询模型[11]通过利用持续最长的相关子序列来判断时间序列的相似性,可以支持对任意长子序列的规范化度量,但是需要非常复杂的索引构建过程.此外,最新的iSAX[9]和iSAX2.0[10]模型基于较早提出的SAX表示方法[6]实现.SAX表示在PAA表示的基础上提取时间序列的数值特征,然后对数值空间离散化,将时间序列变换为符号序列进行处理.与其他表示方法相比,SAX可以结合信息检索领域较成熟的索引结构[17],如倒排索引、前缀树索引等,实现时间序列的近似查询.同时,对数值空间的离散化处理使得SAX具有较好的多分辨率性质,这为构建索引提供了较大的优势.尽管iSAX模型充分利用了SAX的性能优势,但它是一棵非平衡树,索引构建时间将随着数据集的增大而迅速膨胀.尽管iSAX2.0弥补了这一缺陷,但是在查询时随着节点的深入计算,无法保证查询结果的相似性逐步提高,即基于距离下界的剪枝效果得不到改善.

2时序数据表示和索引构建

首先给出时间序列的定义如下.

定义1时间序列变量X在n个连续时刻的采样值序列称为时间序列,表示为T= {t1,t2, …,ti, …,tn},其中ti表示X在第i个时刻的采样值.

2.1特征抽取

基于当前学术界广泛研究的SAX表示方法[6]提取时间序列的特征向量,将时间序列从原始数值空间映射到SAX符号空间.

定义2时间序列特征向量已知时间序列T,若存在f:T→ V = [v1,v2,…,vm] ∈Rm,则向量V称为时间序列T的特征向量.

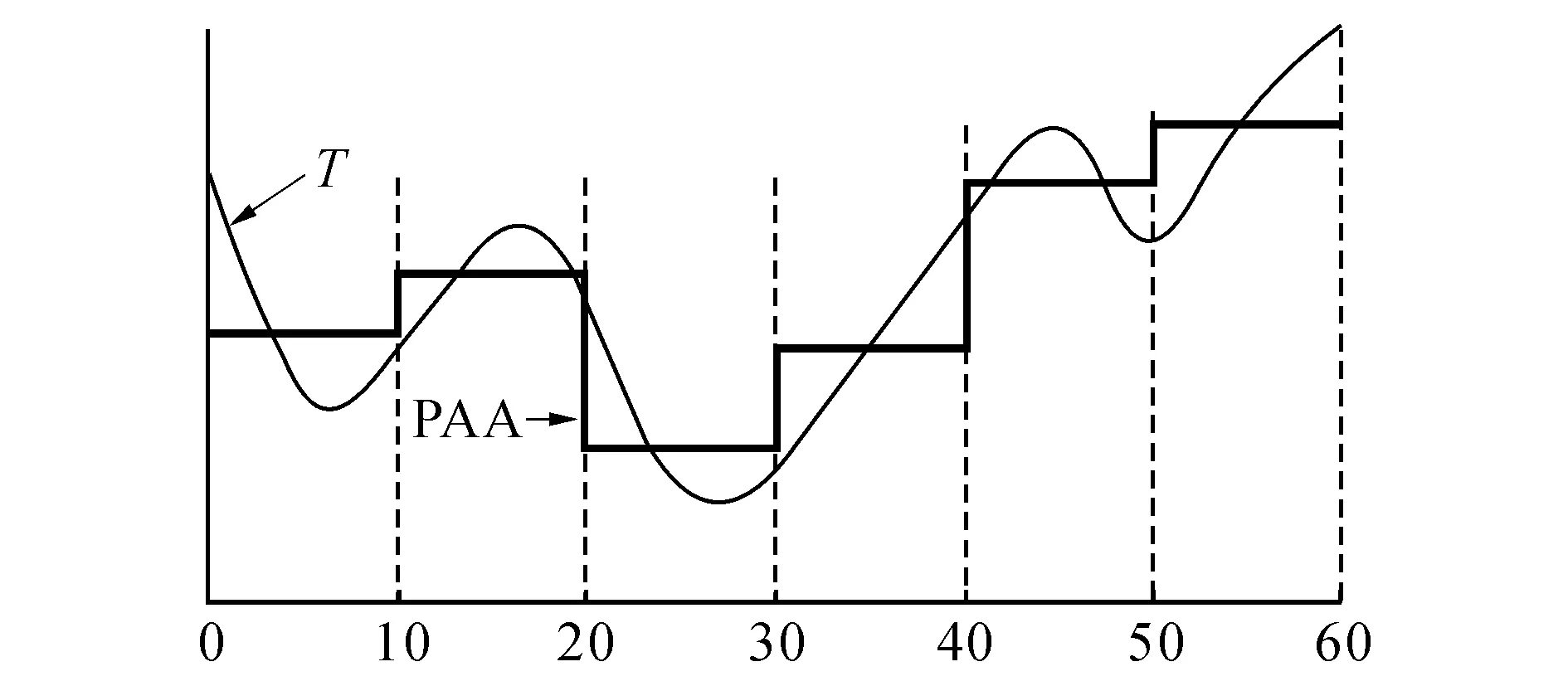
图1　时间序列的分段聚集近似Fig.1　Piecewise aggregation approximation of time series

SAX表示方法是基于PAA表示[5]提出的.在PAA表示中,长度为n的时间序列T被平均划分为w段,通过计算各段元素的平均值得到一个w维的平均值向量,作为T的特征向量：

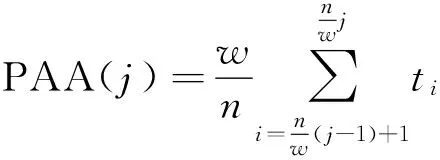
(1)

图1给出长度为60的时间序列以6维PAA特征向量的近似表示.

图2　由PAA表示转化为SAX表示Fig.2　Transformation from PAA to SAX

由于z-规范化的时间序列服从高斯分布,Keogh等[6]基于高斯概率密度函数对实数域作等概率的区间划分,并将各区间以特定的字符表示.将PAA特征向量的各元素映射到对应的划分区间,得到时间序列的SAX特征向量,表示为SAX(T).如图2所示,若将实数域划分为3个区间,由下到上分别以字符{a,b,c}表示,则图2所示的PAA特征向量可以转化为SAX特征向量SAX(T) = [b,b,a,b,c,c].

SAX特征向量采用向量近似文件(VA-File)[18]的组织形式进行编码.VA-File是一种基于空间划分的数据结构,可以在查询过程中实现高效的边界剪枝算法.给定向量集合Φ= {v1, v2,…, vi,…, vm},|vi|表示向量vi的维度,以vij表示vi在第j维的元素值.假设ai是vi的特征向量,以n位存储,则存储ai各元素所需的位数nj可由下式计算得到：

(2)

式中：%表示求模运算.将vi的第j维划分为2nj个区间,整个向量空间Φ划分为2n个元胞.通过将第j维的所有区间依次编号为{0, 1, 2,…, 2nj-1},并以vij所在区间的编号作为其特征aij,得到vi的特征向量ai.VA-File是所有特征向量a1, a2,…, am依次相连构成的二进制字符串.如图3所示,若|vi|=2,n=3,由式(2)可得n1= 2,n2= 1,于是vi的第1维可以划分为4个区间,第2维可以划分为2个区间,整个向量空间被划分为8个元胞.若图3中的向量v3=[9, 3],则特征向量为a3= [1, 0]；对图3中向量集合Φ= {v1, v2, v3, v4, v5}所构建的VA-File为"101110010101111".

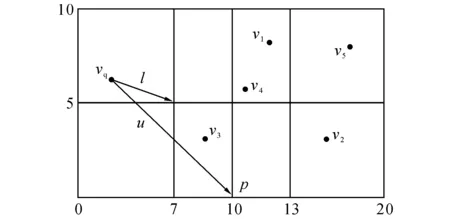
图3　基于VA-File对二维向量空间的划分(|vi|=2, n=3)Fig.3　Division for two-dimensional space based on VA-File

VA-File的显著优点在于基于元胞的上下边界可在高维向量空间中设计高效的剪枝算法,并且有效地克服了“维灾问题”[7].如图3所示,假设查询向量vq=[3, 6],它到向量v3的上、下边界距离l和u分别是vq到v3所在元胞的最近点o和最远点p的距离.

2.2索引构建

针对VA-File引入信息检索领域的倒排索引结构来实现高效查询.倒排索引由单词词表与索引文件构成,单词词表用于维护所有Term,索引文件包含了各Term指向的Postings,各Posting分别包含Term所在的文档及其在该文档内的偏移量.

与传统的倒排索引结构不同,提出基于两种不同粒度SAX特征向量的倒排索引结构,即多粒度时序倒排索引：基于粗粒度的特征向量构建单词词表,基于包含细粒度特征向量的VA-File构建索引文件.目的在于基于粗粒度的SAX特征向量从VA-File中查询出细粒度的SAX特征向量集合作为初始候选集,实现第一级过滤.

定义3 多粒度时序倒排索引假设时间序列Ti分别表示为不同参数的SAX特征向量SAX(Ti)和SAX(Ti),a1插入向量近似文件VAk中.若以SAX(Ti)作为Termj构建单词词表vocabulary,以作为Termj指向的Posting构建索引文件file,其中,σ表示Ti在VAk中的位置偏移量,则由vocabulary与file构成的倒排索引称为多粒度时序倒排索引,表示为MGTI (multi-granularity time inverted-index).

根据信息检索领域较成熟的倒排索引构建算法[17],MGTI的构建过程如算法1所示.

算法1MGTI构建算法

输入：时间序列集合Ф = {T1,T2, …,Ti, …}；SAX参数,.

输出：多粒度时序倒排索引MGTI．

1)遍历Ф,分别将Ti表示为σ=SAX(Ti)和θ= SAX(Ti) .

2) 扫描完毕,获得SAX特征向量对(σ,θ)的集合Λ.

3)遍历Λ,以σ作为主键,以θ作为次键,对Λ元素排序.

抛物线y=ax2+bx+c上有一点C(m，n)，直线l与抛物线交于A，B两点，当∠ACB=90°时，直线l是否经过一定点.

4)将与σi对应的所有θj依次插入链表,作为σi指向的Postings,并存储为VA-File的结构形式VAi;同时,计算θj在VAi中的偏移量σj.

5)将所有σi及对应的Postings指针pi组织为单词词表vocabulary(哈希表或树结构),将所有VAi组织为索引文件file.

6)将作为MGTI并返回.

对于小规模的数据集,MGTI的构建过程可以在内存实现；对于大规模数据集,构建过程需要考虑二级存储操作.对于后者,信息检索领域已经提出较成熟的算法[17],如基于块排序的索引(blocked sort-based indexing)、内存单遍历索引(single-pass in-memory indexing)、分布式索引(distributed indexing)、动态索引(dynamic indexing)等.

3查询处理

针对以上模型,提出两级过滤算法,可以对时间序列实现高效的近似查询.从查询时间序列提取粗粒度SAX特征向量作为查询Term,通过查询MGTI获取与该Term对应的Postings,根据Postings的信息从VA-File中获取查询Term所对应的细粒度SAX特征向量作为初始候选集；提出一种边界剪枝算法过滤初始候选集,得到最终候选集；对最终候选集进行后续处理,即访问原始数据并进行相似性度量,得到查询结果.

定义4 时间序列相似性度量已知时间序列T1和T2,若存在f: (T1,T2) → R+,可以在数值上反映T1与T2之间的形态相似性,则函数f称为时间序列相似性度量,表示为f(T1,T2).

定义5时间序列近似查询已知查询时间序列Q,时间序列数据集合Φ= {T1,T2, …,Ti, …,Tn}及子集S={Ti|Ti∈Φ,f(Q,Ti)≥ε,ε∈R+},若Q经查询算法F得到的结果集合V= {Vi|Vi∈Φ,SV,S∩V≠Ø},则该查询过程称为近似查询.

3.1第一级过滤

定义6初始候选集已知基于参数和,a1的SAX特征向量SAX(T)作为查询Term,则从MGTI得到的参数为的SAX特征向量集合,称为初始候选集,表示为C1.

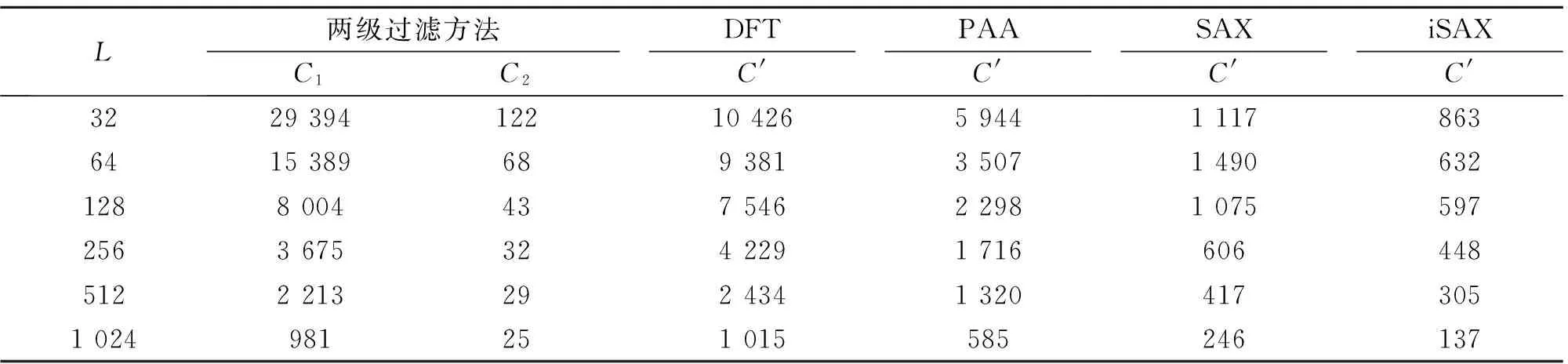
简单查询是指从MGTI中直接获取与查询序列Q的粗粒度SAX特征向量SAX(Q)对应的Postings作为查询结果,见算法2.在第2行中,Q被平均切分为w1条子序列；在第3行计算了每条子序列的平均值,得到Q的PAA特征向量；第4行将PAA特征向量映射到基数为a1的SAX区间,得到Q的SAX特征向量；第5行以Q的SAX特征向量作为Term,查询MGTI获取对应的Postings作为初始候选集C1.若倒排索引的单词词表以哈希表维护,则简单查询的时间复杂度是O(1).

算法2简单查询算法

输入：查询序列Q,SAX参数；

输出：初始候选集C1．

1)C1← Null;

2)S← segment(Q);

3) PAA ← mean(S);

4) SAX ← symbolize(PAA);

5)C1← MGTI(SAX);

6) ReturnC1．

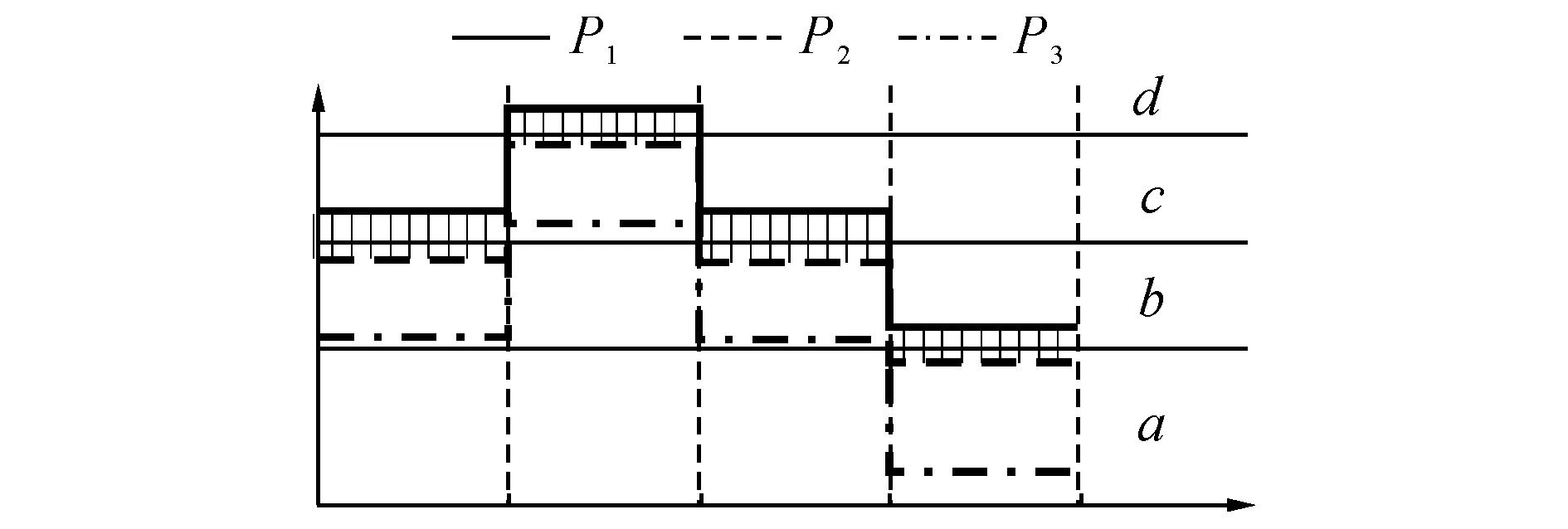
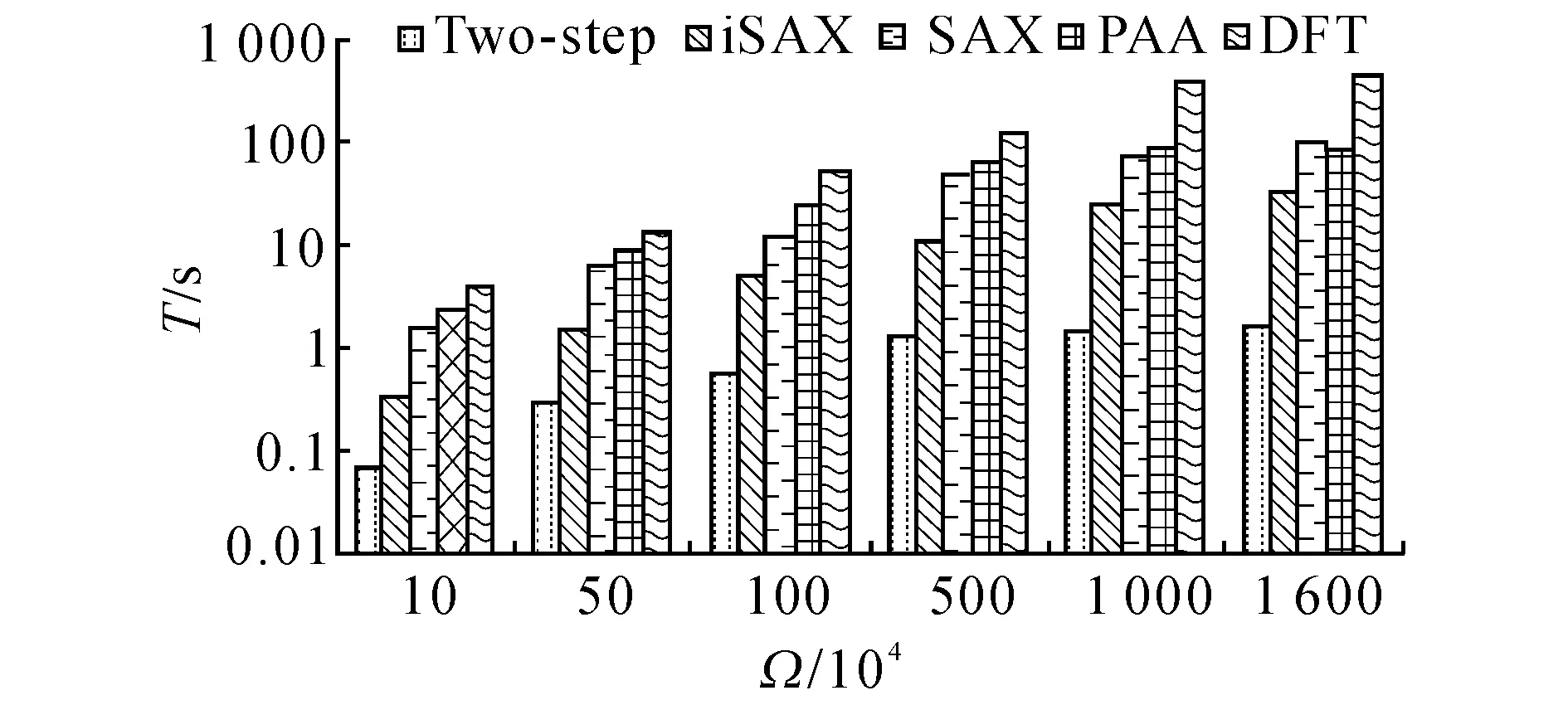
图4　3个PAA特征向量的距离关系示意图Fig.4　Relationship between three PAA feature vectors

虽然简单查询算法具有很高的查询效率,但是在以距离度量作为时间序列相似性评价标准的前提下,简单查询可能会产生较多的“误遗漏”[3].如图4所示,对于PAA向量P1、P2、P3,SAX特征向量分别为SAX(P1) = [c,d,c,b],SAX(P2) = [b,c,b,a],SAX(P3) = [b,c,b,a].若以SAX(P2)作为简单查询算法的输入Term,则初始候选集将包含SAX(P3),而不包含SAX(P1).虽然P1与P2的对应元素分别落在不同的区间,P2与P3的对应元素都落在相同的区间,但是若以欧氏距离作为相似性度量,则有f(P1, P2)

扩展查询是指首先将SAX(Q)的各元素从它所在的SAX区间βj扩展到相邻区间βj-1和βj+1,于是SAX(Q)被扩展到一个SAX特征向量集合Ψ；然后从MGTI中获取与Ψ中各元素对应的Postings集合作为查询结果,见算法3.第3～5行表示基于粗粒度参数提取Q的SAX特征向量；在第6～8行依次扩展SAX特征向量的每个符号元素至相邻的划分区间；在第9行,以集合Ψ中的所有元素作为查询Term,对MGTI执行布尔或查询,获取所有Postings作为初始候选集C1.

算法3扩展查询算法

输入：查询序列Q,SAX参数；

输出：初始候选集C1．

1)C1← Null;

2)Ψ← Null;

3)S← segment(Q);

4) PAA ← mean(S);

5) SAX ← symbolize(PAA);

6) fori← 1:w1

7)Ψ← {SAX[i]-1, SAX[i], SAX[i]+1};

8) end

9)C1← MGTI(Ψ)V;

10) ReturnC1．

算法3等同于对逻辑或的布尔查询,时间开销与Ψ的元素个数成正比.若将SAX(Q)的各元素扩展到γ个相邻区间,则Ψ包含γw个元素,考虑到查询效率,γ不宜过大；在粗粒度的SAX表示中,离散区间较少,因此只需向外扩展一个相邻区间(γ= 3),便能保证细粒度SAX对象的显著增加,即C1的规模增加,由此使得查询精度得到较大提升.

3.2第二级过滤

为了进一步剔除C1的“误命中”,节省后续处理中磁盘I/O的时间开销,基于VA-File的组织结构,提出一种高效的边界剪枝算法对C1进行第二级过滤,以获取规模更小的最终候选集C2,见算法4.

定义7最终候选集已知初始候选集C1= {SAX(T1), SAX(T2),…, SAX(Tn)},若存在算法F,以C1作为输入,以集合C2作为输出,并且C2⊆C1,则C2称为最终候选集.

算法4基于VA-File的边界剪枝算法

输入：查询序列Q,初始候选集C1；

SAX参数；

输出：最终候选集C2．

1.C2← Null;

2. MaxUpper ← zeros[k];

3. MinLower ← Null;

4. query ← SAX(Q);

5. fori← 1:k

6.l← low_boud(query,C1[i]);

7.u← up_boud(query,C1[i]);

8. MaxUpper ←u;

9. MinLower ← (C1[i],l,u);

10. end

11. fori←k+1:n

12.l← low_boud(query,C1[i]);

13. ifl< MaxUpper[1]

14.u← up_boud[query,C1(i)];

15. MaxUpper ←u;

16. MinLower ← (C1[i],l,u);

17. end

18. end

19. forj← 1:m

20. if MinLower[j] > MaxUpper[1]

21. break;

22. else

23.C2← MinLower[j];

24. end

25. end

26. ReturnC2．

在算法4中,第2和第3行分别构建了容量为k的最大优先队列MaxUpper和最小优先队列MinLower；第4行基于参数提取Q的SAX特征向量；第6和第7行分别计算query与C1第i个元素的上下边界距离；在第9行根据下界距离对C1的前k个元素进行排序；在第20行判断MinLower中第j个元素的下界距离与MaxUpper中当前最大上界距离的关系；在第23行取出MinLower的第j个元素对应的时间序列插入最终候选集C2.算法4是一种基于边界距离的剪枝算法,满足下界定理[7]可知,不会导致“误遗漏”,计算复杂度为O(n+mlog2m),其中n为C1的元素数目,m为C2的元素数目.另外,算法4可以采用多种提前终止技术[16]及内存表技术[6]进行加速计算.

4实验分析

4.1实验设置

实验环境：Intel(R) Core(TM) i5-2400 CPU @ 3.10 GHz,8 GB内存,Windows 7 64位操作系统.模型基于Java语言和开源的Lucene 4.6.0框架实现.原始数据集全部存储于基于MYISAM存储引擎的数据库管理系统MySQL 5.6.17中,并通过JDBC读取数据.实验采用以下两类数据集.

1)真实股票数据集,从Yahoo! Finance[19]获取的美国NASDAQ证券交易市场的5031个上市公司在1962/1/2至2013/12/03期间的股票日收盘价格序列.对所有股票序列进行z-规范化处理,并切分为不重叠的子序列集合,得到6种不同序列长度L的数据集所包含的序列数目Ω,如表1所示.

表1　不同序列长度的真实股票数据集

2)随机游走数据集：按照公式o[i+1]=o[i]×[1+N(μ,σ)][20]生成序列长度为256的随机游走数据集,其中N(μ,σ)为正态分布函数,选择默认参数为均值μ= 0,标准差σ= 0.2[11].生成了6个不同规模Ω的数据集,分别包含10万条、50万条、100万条、500万条、1 000万条、1 600万条时间序列.

在时间序列相似性查询研究中,查询结果的漏报率(false dismissal rate, FDR)是衡量查询完备性的重要指标[3].本文模型仅在第一级过滤中引入“误漏报”,而第二级过滤算法满足下界定理,不会进一步造成“误漏报”,模型的漏报率只需通过初始候选集进行检验.采用P@N(Precision@N)指标[17]对查询结果的准确率进行检验.每次查询的ground-truth全部基于欧氏距离从原始数据集找出.

时间序列相似性查询模型的时间开销主要集中在后续处理的磁盘I/O上,候选集规模越大,磁盘I/O的开销越大,因此模型的查询效率实际由候选集规模决定,前者可以通过后者进行检验.

在构建模型时,需要对MGTI的SAX特征向量维度w和特征空间基数a选择两组不同粒度的参数,即和,其中w1决定词典的大小以及第一级过滤的候选集大小,为了避免数据空间过于稀疏,对于所用实验的数据集规模,取值不宜过大；同时,扩展查询算法的时间开销需要控制在较低的水平,为此首先确定w1=4,然后通过检验模型的召回率来选择参数a1.的大小决定了VA-File中元胞边界的紧凑度,进一步决定了第二级过滤的性能,其中,取值越大,性能越好；实验数据集的最小序列长度为L=32,为了保证SAX表示对数据空间的压缩作用(即保证较低的索引开销),选择w2=16,a2=16.

4.2实验结果及分析

4.2.1参数影响由于模型的查询精度由决定,在确定参数w1的情况下,检验模型在7个不同序列长度的真实股票数据集上采用扩展查询算法执行Top-20的kNN查询,模型的召回率R随特征空间基数a1的变化情况,如图5所示.

图5　模型召回率随特征空间基数a1的变化情况Fig.5　Recall variation with space cardinality a1

由图5可知,随着参数a1的增大,模型召回率逐渐下降.原因在于参数a1越大,SAX对数据空间的划分越细,空间越稀疏,查询到的初始候选集越小,所包含的真实结果越少,召回率越低.在参数a1的各取值上,模型在7个不同序列长度数据集上的召回率相差较小,说明模型对时间序列长度具有鲁棒性.为了保证模型具有较高的召回率,选择参数a1=8用于后续实验.

4.2.2有效性检验模型分别基于6个不同序列长度的数据集对简单查询与扩展查询算法执行Top-20、Top-40、Top-60的kNN查询,以检验漏报率RFD.实验结果如图6所示.

图6　模型漏报率检验结果Fig.6　Evaluation results for dismissal rate

由图6可得以下结论.1)模型基于简单查询与扩展查询的漏报率差距较大,因此扩展查询比简单查询算法更加有效；2)在不同序列长度的数据集上,模型执行kNN查询的漏报率相差较小,说明模型对kNN查询规模具有鲁棒性.原因在于SAX采用等概率的区间划分,相似时间序列的SAX特征向量在MGTI中会以较高的概率落在同一个或相邻的Term所对应的Postings中,随着k的增大,被查询出的相似时间序列的概率保持了较高的稳定性.

基于P@N指标对模型(基于扩展查询算法)的有效性检验结果如图7所示.图中，P为查准率.由图7可得以下结论.1)模型在不同规模的kNN查询中,都能保持较高的查准率(>0.8)；2)每条曲线都比较平缓,说明模型对kNN查询规模具有鲁棒性；3)在不同序列长度的数据集上,执行同样kNN查询的查准率相差较小,说明模型对时间序列长度具有鲁棒性.在实验中,模型对不同长度的时间序列采用了统一的SAX特征向量维度参数w1和w2,而模型的查准率是由SAX特征向量对原始时间序列的近似精度决定的,因此模型的查准率对时间序列长度的稳定性来源于SAX表示方法的近似精度对时间序列长度的稳定性.

图7　模型查准率检验结果Fig.7　Evaluation results for precision rate

4.2.3查询性能检验实验基于6个不同序列长度的真实股票数据集开展Top-20的kNN查询,以分别基于DFT[7]、PAA[5]、SAX[6]的精确查询模型以及iSAX[9]近似查询模型作为对比方法.表2呈现了5种方法查询生成的候选集大小(时间序列数目).

由表2可得如下结论.1)对于本文模型,初始候选集的数目C1较大,但是最终候选集的数目C2远小于所有对比方法生成的候选集数目C′；2)随着时间序列长度的增加,C2始终维持在较低的水平,说明模型的查询性能对时间序列长度具有鲁棒性.由于两级过滤方法在MGTI中采用了两种粒度的SAX特征向量,逐渐细化的参数使得SAX下界紧凑度越来越高,由此保证了模型对不相似时间序列具有较强的滤除能力.

基于6个不同规模的随机游走数据集对5种模型分别执行Top-20的kNN查询,以检验它们的实际查询时间开销T,结果如图8所示.

由图8可得如下结论.1)本文模型的查询性能比4种对比方法的性能最多高出2个数量级,很明显导致这一差距的主要因素是查询过程中的候选集规模差别较大； 2)本文模型在不同规模数据集上的查询时间始终维持在较低的水平,因此模型的查询性能对数据集规模具有较强的鲁棒性.

表2　各种查询模型在不同数据集上的候选集大小

图8　5种方法的实际查询时间开销比较Fig.8　Runtime comparison between five models

5结语

本文基于多粒度的SAX表示,提出基于两级过滤的时间序列相似性查询模型,构建多粒度倒排索引结构,并设计启发式的查询过滤算法,用于实现高效高精度的近似查询.

下一步的研究工作将围绕范围查询深入展开,并且如何将模型有效地应用于超大规模时间序列数据集的问题,有待进一步的深入研究.

参考文献(References)：

[1] ESLING P, AGON C. Time-series data mining [J]. ACM Computing Surveys, 2012, 45(1): 1-34．

[2] CONG F, CHEN J, DONG G, et al. Short-time matrix series based singular value decomposition for rolling bearing fault diagnosis [J]. Mechanical Systems and Signal Processing, 2013, 34(1): 218-230．

[3] AGRAWAL R, FALOUTSOS C, SWAMI A. Efficient similarity search in sequence databases [J]. Foundations of Data Organization and Algorithms, 1993, 730(1): 69-84．

[4] CHAOVALIT P, GANGOPADHYAY A, KARABATIS G, et al. Discrete wavelet transform-based time series analysis and mining [J]. ACM Computing Surveys, 2011, 43(2): 1-37．

[5] KEOGH E, CHAKRABARTI K, PAZZANI M, et al. Dimensionality reduction for fast similarity search in large time series databases [J]. Knowledge and Information Systems, 2001, 3(3): 263-286．

[6] LIN J, KEOGH E, WEI L, et al. Experiencing SAX: a novel symbolic representation of time series [J]. Data Mining and Knowledge Discovery, 2007, 15(2): 107-144．

[7] FALOUTSOS C, RANGANATHAN M, MANOLOPOULOS Y. Fast subsequence matching in time-series databases [C]∥Proceedings of the 1994 ACM SIGMOD International Conference on Management of Data. New York: ACM, 1994: 419-429．

[8] ATHITSOS V, PAPAPETROU P, POTAMIAS M, et al. Approximate embedding-based subsequence matching of time series [C]∥ Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data. New York: ACM, 2008: 365-378．

[9] SHIEH J, KEOGH E.iSAX: disk-aware mining and indexing of massive time series datasets [J]. Data Mining and Knowledge Discovery, 2009, 19(1): 24-57．

[10] CAMERRA A, SHIEH J, PALPANAS T, et al. Beyond one billion time series: indexing and mining very large time series collections with iSAX2+ [J]. Knowledge and Information Systems, 2013, 39(1): 1-29．

[11] LI Y, YIU M L, GONG Z. Discovering longest-lasting correlation in sequence databases [J]. Proceedings of the VLDB Endowment, 2013, 6(14): 1666-1677．

[12] KEOGH E, CHAKRABARTI K, PAZZANI M, et al. Locally adaptive dimensionality reduction for indexing large time series databases [J]. ACM SIGMOD Record, 2001, 30(2): 151-162．

[13] KEOGH E, CHU S, HART D, et al. Segmenting time series: a survey and novel approach [J]. Data Mining in Time Series Databases, 2004, 57(1): 1-22．

[14]GULLOF,PONTIG,TAGARELLIA,etal.Atimeseriesrepresentationmodelforaccurateandfastsimilaritydetection[J].PatternRecognition, 2009, 42(11): 2998-3014．

[15]PAPADIMITRIOUS,SUNJ,FALOUTSOSC.Streamingpatterndiscoveryinmultipletime-series[C]∥Proceedingsofthe31stInternationalConferenceonVeryLargeDataBases.NewYork:ACM, 2005: 697-708．

[16]RAKTHANMANONT,CAMPANAB,MUEENA,etal.Searchingandminingtrillionsoftimeseriessubsequencesunderdynamictimewarping[C]∥Proceedingsofthe18thACMSIGKDDInternationalConferenceonKnowledgeDiscoveryandDatamining.NewYork:ACM, 2012: 262-270．

[17]MANNING,CHRISTOPHERD,PRABHAKARR,etal.Introductiontoinformationretrieval[M].Cambridge:CambridgeUniversityPress, 2008．

[18]BLOTTS,WEBERR.Asimplevector-approximationfileforsimilaritysearchinhigh-dimensionalvectorspaces[R].Zurich:ETHZentrum, 1997．

[19]YAHOO!Finance. [2015-05-01].http:∥finance.yahoo.com/.

[20]MonteCarlosimulatedstockpricegenerator. [2015-05-01].http:∥25yearsofprogramm-ing.com/．

收稿日期：2015-05-13.浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

基金项目：中国工业和信息化部“核高基”重大专项基金资助项目(2010ZX01042-002-003-001)；中国工程科技知识中心基金资助项目(CKCEST-2014-1-5)；国家自然科学基金资助项目(61332017).

作者简介：蔡青林(1987-)，男，博士生，从事数据挖掘、信息检索、模式识别的研究. ORCID：0000-0001-5219-7771. E-mail: qlcai@zju.edu.cn 通信联系人：陈岭，男，副教授. ORCID：0000-0003-1934-5992. E-mail: lingchen@zju.edu.cn

DOI:10.3785/j.issn.1008-973X.2016.07.010

中图分类号：TP 39

文献标志码：A

文章编号：1008-973X(2016)07-1290-08

Two-step filtering based time series similarity search

CAI Qing-lin, CHEN Ling, MEI Han-lei, SUN Jian-ling

(CollegeofComputerScienceandTechnology,ZhejiangUniversity,Hangzhou310027,China)

Abstract:A two-step filtering based search model was proposed in order to solve the problms that existing approximated search models have the poor controllability on the accuracy and have the low efficiency at the post-processing step. The symbolic aggregate approximation (SAX) method was employed to extract the symbolic feature vectors from time series. The high-dimensional time series was projected into the low-dimensional feature space. The symbolic feature vectors were saved as the form of vector approximation file (VA-File), and the efficient inverted index was introduced. A heuristic query and filtering algorithm was proposed at the procedure of searching in order to perform the first filtering, and an efficient boundary pruning method was proposed over the VA-File to reach the second filtering. The model can effectively control the search accuracy by the SAX feature vectors with multiple precision. Experimental results show that the proposed model has the efficient performance and the robust scalability on the series length, the kNN query scale and the dataset size．

Key words:time series; similarity search; symbolic aggregation approximation; vector approximation file; inverted index