基于整体风险的组合套期保值模型的研究

杜建慧

（山西农业大学信息学院，山西 太谷 030800）

基于整体风险的组合套期保值模型的研究

杜建慧

（山西农业大学信息学院，山西 太谷 030800）

本文建立了基于整体风险控制的组合套期保值优化模型，通过控制套期保值收益率的 偏度和峰度，使套期保值收益率密度函数的尾部向右拉长而左端的尾部较短，峰度不至于太尖，从而避免了收益率尖峰厚尾的情况，使收益率分布降低了负收益的概率同时增加了正收益的概率，即减小了套期保值发生重大损失的概率。本模型通过差分进化算法求解，检验表明，模型是合理的，算法是有效的。

整体风险；组合套期保值；商品期货；条件风险价值

0　引 言

套期保值（简称套保）是利用一定比例的期货合约与现货头寸（多头或空头），通过对冲交易来规避现货价格风险的一种策略。用于套期保值的金融工具有很多，目前多数是使用现货商品所对应的期货和期权进行套期保值。人们把同时使用期货和期权对现货进行套期保值的策略称为组合套期保值。近年来国内学者又提出了最大效用套期保值和套期保值比率等问题.以前的研究基本都是建立在方差风险的基础上，有些只考虑了偏度的影响。本文则提出了考虑偏度风险和峰度风险的期货套期保值模型。

1　基于整体风险的组合套期保值模型的建立

笔者假设要对某件商品进行套期保值，该商品的现货价格为S，设选用n种期货X1，X2，…，Xn，进行套期保值交易，期货的价格分别为F1，F2，…，Fn，套期保值比率为h1，h2，…，hn，即1单位的现货商品要用h1单位的期货X1，h2单位的期货X2，…，hn单位的期货Xn来对冲其价格波动风险。

2.1 组合套期保值收益率的确定

由于对数收益率能更准确地反映平稳收益的分布，下面笔者采用对数收益率来表示现货和期货的收益率。设第t个交易日现货收益率为Rs，t=ln（St）-ln（St-1），期货收益率为RF，t=ln（Ft）-ln（Ft-1），其中ln（x）为自然对数函数，St为第t个交易日现货的价格，Ft为第t个交易日期货的价格。由于用n种期货进行套期保值，故记RF，t=（RF1，t， RF2，t，…， RFn，t）。设hi为第i种期货对现货的套期保值比率，H为不同期货对现货的套期保值比率所组成的列向量，则。设Rs为现货收益率，RFi为第i种期货的收益率，RF为期货组合中不同期货的收益率组成的列向量，则。假设期货的固定单位交易费用为c，期货组合的交易费用可以表示为，那么n种期货对一种现货的组合套期保值收益函数Rh为Rh=Rs-HTRF-|H|TC。

2.2 组合套期保值收益率期望和方差的确定

设E（Rs）为现货的期望收益率，E（RF）为期货的期望收益率，E（C）为期货交易费用的期望收益率，则套期保值后收益率的期望为：

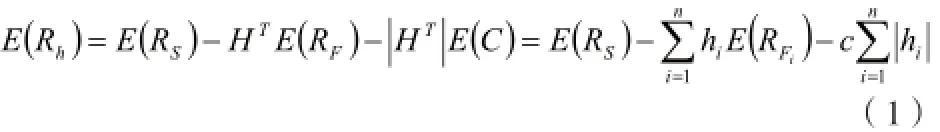
设σ（Rs）为现货收益率的方差，σ（RF）为期货收益率的方差，则套期保值后收益率的方差为：

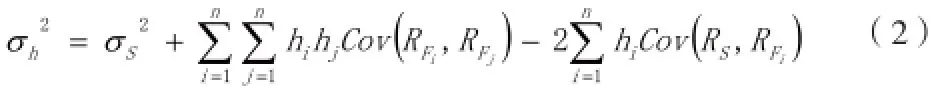
2.3 收益率偏度、峰度的计算与经济学意义

套期保值收益率Rh的偏度是收益率的三阶中心矩除以收益率标准差的三次幂，它的计算公式为：

套期保值收益率Rh的峰度是收益率的四阶中心矩除以收益率标准差的四次幂，它的计算公式为：

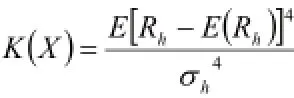
收益率峰度反映随机变量分布尾部的厚度，正态分布的峰度常数为3，均匀分布的峰度常数为1.8。若K（X）＞3，说明X分布的尾部比正态分布的尾部厚，这意味着来自这样一个分布的随机样本会有更多的极端值，发生损失的概率就增加了。反之，若K（X）＜3，则发生极端风险的概率也就降低了。

2.4 基于整体风险的组合套期保值模型

笔者采用标准正态分布下的CVaR值来作为模型的目标函数，同时考虑组合套期保值的偏度和峰度作为约束条件，由基于整体风险的组合套期保值原理可得本文的模型：

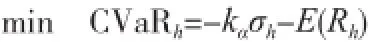
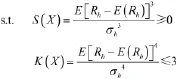
3　差分进化算法设计

差分进化算法是Rainer Storn和Kenneth Price为求解切比雪夫多项式于1995年共同提出。它是一种模拟生物进化的随机模型，通过反复迭代，使那些适应环境的个体被保存下来.差分进化算法具有较强的全局收敛能力和鲁棒性，适于求解一些利用常规的数学规划方法所无法求解的复杂环境中的优化问题。目前已经在人工神经元网络、机械设计、机器人、信号处理、经济学、食品安全和运筹学等领域得到了应用.具体算法步骤如下。

Step 1：初始化设置最大迭代次数以及相关参数。

Step 2：初始化每个个体，并计算其目标函数值fi和约束违反度值Gi。

Step 3：根据可行基规则来找出初始粒子群的全局极值gbf、全局最优解gbx，及全局最优粒子的约束违反度值Ggbest。

while （迭代次数t＜最大迭代次数Tmax）does。

Step 6：计算每个新粒子的目标函数值fi和约束违反度值Gi，根据动态目标约束处理技术更新粒子的全局极值gbf、全局最优解gbx，及全局最优粒子的约束违反度值Ggbest。

t=t+1

End while

输出全局极值gbf和全局最优解gbx。

4　组合套期保值实证研究与结果分析

笔者采用大豆和豆粕期货来对豆油现货进行交叉套期保值，数据均采用某年1月5日至12月14日共228个交易日的数据，具体数据见表1。以上现货数据据来自天琪期货网站，期货数据来自大连商品期货网站。

本文模型对比分析的参照物是不进行套期保值和一对一套期保值的单位风险、有效性、收益率偏度和峰度。将数据代入相应的公式，可得相关参数，见表1。

表1 对比研究的计算结果

通过表1的计算结果，可得如下结论。

第一，从表第3列可以看出本模型套期保值的单位风险收益最高。这说明进行组合套期保值提高了单位风险收益。

第二，从表第4列可以看出通过相关性强的期货组合进行组合套期保值提高了套期保值的有效性。

第三，从表第5列和第6列可以看出本模型较接近于正态分布，避免了尖峰厚尾的情况，从而通过偏度和峰度控制了收益分布尖峰厚尾发生极端损失的情况。

5　结 语

本文给出了一个基于整体风险控制的组合套期保值优化模型，考虑到偏度和峰度对于套期保值的影响，通过相关性强的期货组合进行组合套期保值，并用差分进化算法进行了求解，大大提高套期保值的有效性。本文建立的组合套期保值优化模型，解决了用一种期货对一种现货进行交叉套期保值时很难找到与现货价格相关性强的期货品种，进而无法有效进行套期保值的问题。因此，基于上述考虑，本文所提出的模型更加符合投资者的实际行为，为决策者提供了可行的方案，是一个合理的模型。

主要参考文献

［1］迟国泰，杨中原，王玉刚.基于重大损失控制的套期保值优化模型［J］.预测，2007（6）.

［2］迟国泰，赵光军，杨中原.基于CvaR的期货最优套期保值比率模型及应用［J］.系统管理学报.2009（1）.

［3］R Storn，K Price.Differential Evolution-A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces［J］.Journal of Global Optimization，2010 （4）.

10.3969/j.issn.1673 - 0194.2016.10.075

F224；F713.35

A

1673-0194（2016）10-0109-02

2016-04-02