蚁群BP神经网络的光伏电站辐照强度预测

贺 文，齐 爽，陈厚合（.国网宁夏电力公司，银川 75000；.东北电力大学电气工程学院，吉林 30）

蚁群BP神经网络的光伏电站辐照强度预测

贺 文1，齐 爽2，陈厚合2
（1.国网宁夏电力公司，银川 750001；2.东北电力大学电气工程学院，吉林 132012）

摘要：为了提高光伏电站辐照强度的预测精度，本文提出了基于蚁群改进BP神经网络的预测方法。首先，分析了辐照强度的影响因素，从中筛选出纬度、海拔、天气类型、日照时数、温度、空气质量、相对湿度、风速、大气压强等最优影响因子作为模型的输入；其次，通过建立新的传递函数，采用最小均方误差能量函数法进行自动优化隐含层数；按月份建立蚁群改进BP神经网络模型，对辐照强度进行预测。预测结果与BP神经网络模型进行对比，表明该方法有效提高了辐照强度的预测精度。

关键词：光伏电站；辐照强度；蚁群算法；改进BP神经网络；预测

太阳能是绿色可再生能源，光伏发电系统很好地利用了太阳能的清洁性与经济性，已经受到了各国的重视。随着光伏发电并网规模的不断扩大，光伏发电系统功率的输出对电网的影响也日益凸显。光伏发电功率预测的准确与否直接关系到电力系统调度部门能否及时合理安排电网运行方式，从而采取措施调整调度计划，以提高电力系统的安全性与稳定性［1-2］。

目前，光伏发电功率预测的方法有两种：一种是直接预测方法，利用光伏电站的历史输出功率进行预测；另一种是间接预测方法，基于辐照强度预测光伏发电系统的输出功率。间接预测方法依赖于复杂的辐照强度预测模型和精准的气象预报信息，目前尚未成熟［3］。因此，若能准确预测光伏电站辐照强度，将会降低光伏电站并网时对电网的影响，从而保证电力系统的可靠性与经济性。

目前人工神经网络ANN（artificial neural net⁃work）［4-6］模型在辐照强度预测方面取得了较大的成就。尤其是应用广泛的BP（back propagation）神经网络，它具有自组织、自适应和自学能力，特别适用于处理需要同时考虑许多因素和不精确条件的模糊信息问题。但是BP神经网络算法有它自身的局限性，例如局部搜索能力使其易陷入局部极小值、收敛时间长、泛化能力弱等缺点。有研究证明，两种或两种以上的组合预测优于单个预测效果，可以提高预测精度［7-8］。

本文提出了基于蚁群改进BP神经网络的光伏电站辐照强度预测方法，分析了辐照强度的多个重要影响因子，将其作为模型的输入变量，并创建新的网络函数，实现网络结构自动优化确定。利用石嘴山第四光伏发电站历史数据，验证了该预测方法的准确性与稳定性。

1 蚁群改进BP神经网络基本原理

1.1 BP神经网络基本原理

BP神经网络由输入层、隐含层、输出层构成［9］。它能够以任意精度逼近非线性映射，是一种以信号传播为基础的学习过程，信号在传播的过程中可分为正向传播和反向传播两种过程：

（1）正向传播过程：输入数据通过隐含层的处理映射，在输出层计算实际输出值；

（2）反向传播过程：当输出层没有得到误差允许范围内的输出值时，BP神经网络将逐层递归计算实际值与期望值的差值（误差），然后根据差值将其错误部分反方向传播，在反方向传播过程中处理各个单元的错误信号，从而获得其中的误差信号。重复其过程，若输出值与期望值接近，则训练结束。

1.2 蚁群算法基本原理

蚁群算法ACA（ant colony algorithm）［10-11］是一种模拟蚂蚁群从巢穴到达食物源寻找最优路径的搜索优化算法。蚂蚁在觅食过程中释放的信息素具有通讯功能。通过信息素的累积而形成的正反馈机制的调节作用，加快了系统寻找最优解的速度，使蚂蚁觅食路径向全局最优的方向进行，从而获得全局的相对最优解。此外，该算法采用分布式并行计算，对问题的解进行全局搜索，避免了局部极小值问题。

1.3 蚁群算法与BP神经网络相结合的基本原理

BP神经网络随机产生初始权值和阈值，若初值选择不当，会使网络收敛速度缓慢或不收敛，或者得到一个局部最小解而非全局最优解。BP神经网络采用梯度下降法对网络的权值和阈值进行修正来寻求最优解，因此会出现振荡，网络性能下降，学习速度慢，陷入局部极小值等问题。蚁群算法具有智能全局搜索优化能力，并有较好的鲁棒性等优点。用蚁群算法训练BP神经网络的权值和阈值，可兼有BP神经网络的非线性映射能力和蚁群算法的全局优化能力，克服了BP神经网络的缺点。

2 输入变量的选取

辐照强度预测是一个复杂的非线性问题，辐照强度的大小由许多因素共同决定，因此提高辐照强度预测精度的关键是选择最优的影响因子。近年，雾霾等天气的出现，空气质量急剧下降，直接影响了太阳能的辐射。空气质量指数AQI（air quality in⁃dex）是定量描述空气质量状况的无量纲指数，指数越大，对太阳能辐照强度的影响越大。故本文重点对纬度、海拔、天气类型、日照时数、温度、空气质量、相对湿度、风速、大气压强进行研究，分析这些因素对辐照强度的影响。

2.1 天气类型对光伏电站辐照强度的影响

不同天气类型对辐照强度大小影响很明显，如图1所示。本文选取了4种天气类型的辐照强度，晴天的辐照强度规律性很强，基本呈正态分布，辐照强度平均值很大，最大值达到900 W/m2左右；多云天气类型的辐照强度变化没有规律，随机性、波动性很强，这给辐照强度的预测增加难度；小雨/阴、阵雨/中雨等天气类型的辐照强度时刻都在变化，且辐照强度平均值很小，最大值在300 W/m2左右，这会对光伏并网运行的安全稳定性造成影响。

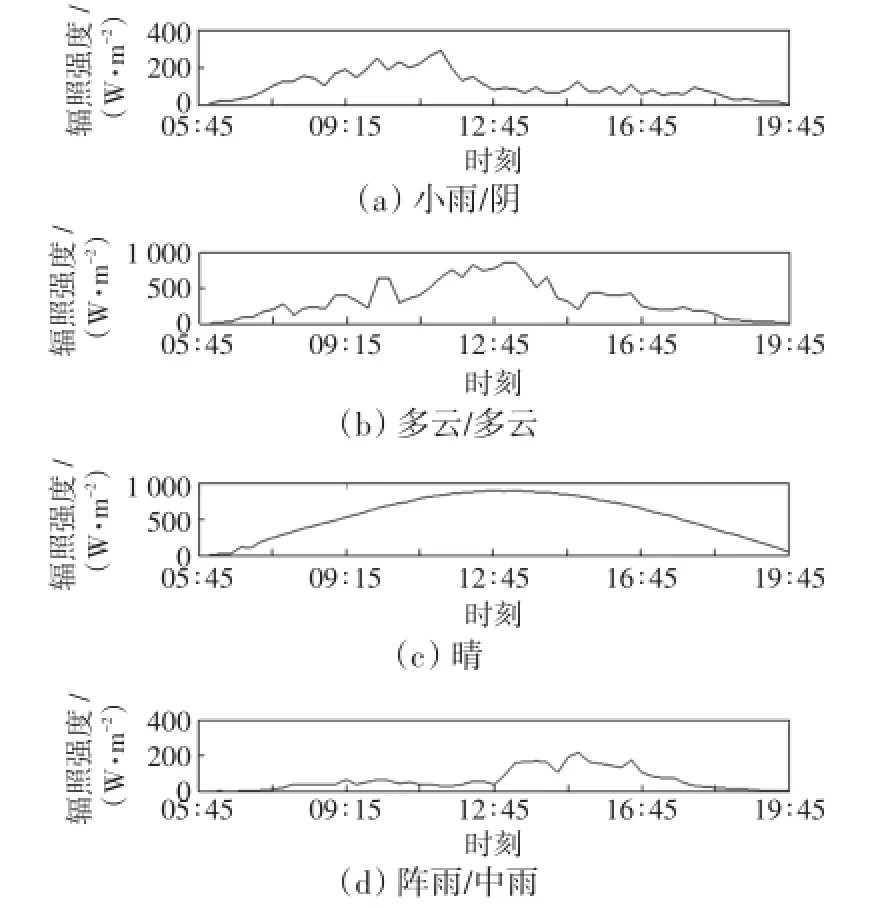
图1 辐照强度与天气类型的关系曲线Fig.1 Curves of relationship between radiation intensity and weather type

由于不同天气类型的辐照强度和变化规律相差很大，所以考虑天气类型越全面，预测结果的精度越高。本文把天气预报基本出现的天气类型进行总结，归纳出49种常见的天气类型（见表1），如晴天、晴/云、多云/晴等。类似于晴/雷阵雨归类于晴/小雨；冬天的辐照强度值相对较小，所以晴/大雪、晴/中雪和晴/小雪归为晴/雪一类，减小了信息冗杂。

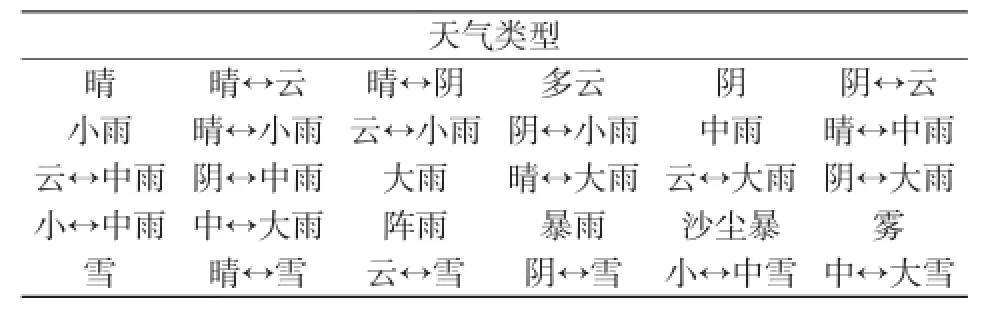
表1 49种常见天气类型Tab.1 49 common types of weather

2.2 温度对光伏电站辐照强度的影响

温度对辐照强度的影响如图2所示。由于温度和辐照强度的单位和数量级都不同，直接检验两者的关系效果不明显，把温度和辐照强度的数据进行归一化处理。选取石嘴山第四光伏发电站2013 年6月24日的数据进行检验，由图2可知，温度曲线与辐照强度曲线的走势相似，温度对辐照强度具有正相关性，故把温度作为预测模型的输入变量。

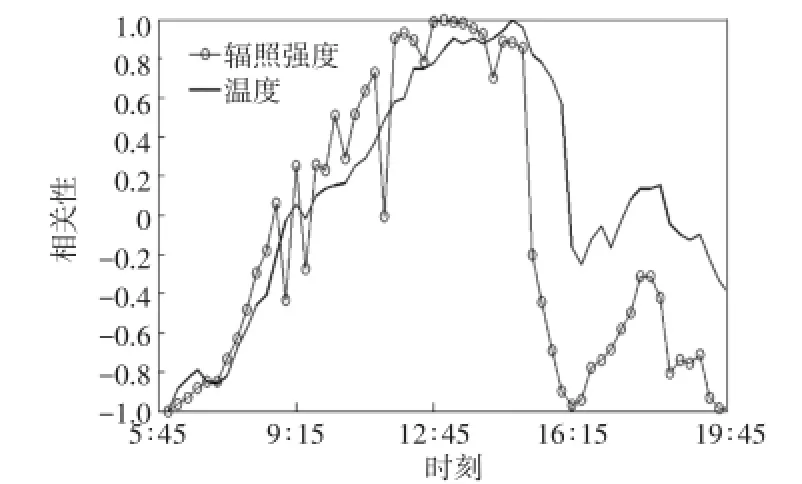
图2 辐照强度与温度相关性曲线Fig.2 Correlation curves between radiation intensity and temperature

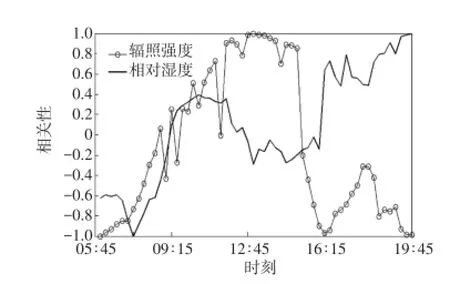
图3 辐照强度与相对湿度相关性曲线Fig.3 Correlation curves between radiation intensity and relative humidity

2.3 相对湿度和风速对光伏电站辐照强度的影响

选取石嘴山第四光伏发电站2013年6月24日的数据，在天气类型、温度相同的情况下，环境的相对湿度和风速与辐照强度的关系如图3和图4所示。由图可知，环境的相对湿度和风速与辐照强度呈现负相关性，相对湿度越小，辐照强度越大；风速变化越缓和，辐照强度越大。故本文把相对湿度和风速作为预测模型的输入变量。

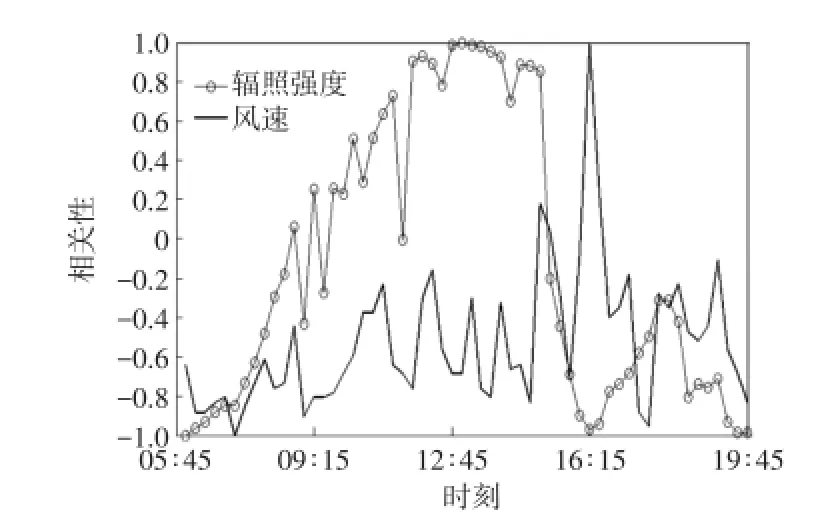
图4 辐照强度与风速相关性曲线Fig.4 Correlation curves between radiation intensity and wind speed

2.4 其他因素对光伏电站辐照强度的影响

位置的不同，太阳能到达地面的辐射强度不同。纬度高低，影响太阳高度角的大小，高度角大小又影响着辐射强度；海拔高与大气稀薄度成反比，海拔高的地方到达地面的太阳辐射强。日照时数的长短直接影响太阳能辐射强度。大气压强与季节、天气类型、温度、空气密度等因素有关，它是一个综合影响因素，故把纬度、海拔、日照时数、大气压强作为预测模型的输入变量。

3 蚁群与改进BP神经网络的设计

3.1 建立新传递函数

BP神经网络中传递函数的作用是模拟生物神经元所具有的非线性传递特征，传递函数的选取不当可能导致收敛速度慢、局部极小值等问题。本文建立了新的传递函数—Sch函数为

f（x）在坐标原点附近具有较陡和较宽的峰，能将（-∞，+∞）的输入分别映射到（0，1）中。由于辐照强度没有负值且信息分布存储在各神经元传递函数中，在神经元个数不变时，Sch传递函数比BP神经网络中的传统函数具有更好的非线性映射能力，同时增强了大规模并行信息处理能力。由于网络的拓扑结构不会变，当网络计算输出值和期望值接近时，不需要大量的附加运算，使运算速度加快。

3.2 网络结构优化确定

辐照强度的数据虽然具有非平稳性，但曲线整体呈现正态分布，本文选用的网络结构为3层，建立能够容纳庞大样本数据的预测模型，以辐照强度、纬度、海拔、天气类型、最高温度、最低温度、空气质量、相对湿度、风速、日照时数、大气压强作为模型的输入，网络的输出为

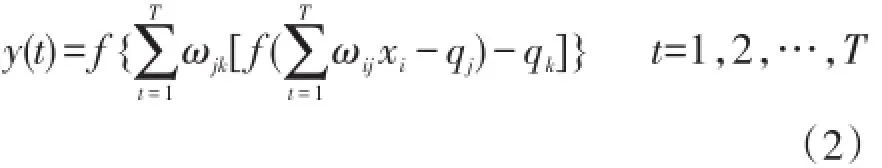
式中：y（t）为网络第t个节点的输出值；ωij和ωjk分别为网络输出层到隐含层的连接权值、隐含层到输出层的连接权值；qj和qk分别为网络输出层到隐含层的阈值、隐含层到输出层的阈值；T为Sch函数的个数，通过最小均方误差能量函数进行优化确定。最小均方误差公式为

式中：y*（t）为辐照强度的实测值；T采用逐步检验法确定。在预测前给定一个拟合误差值H，若最小均方误差小于H，则T取值1，计算t的值。若t＜H，则T=1；反之，T取值2，以此类推，逐步取值直到T=T*值，ET*＜H，若取值T=T*+1时，ET*+1＞H，此时的T*为最优模式数，即最优隐含层个数。本文的蚁群改进BP神经网络结构如图5所示。

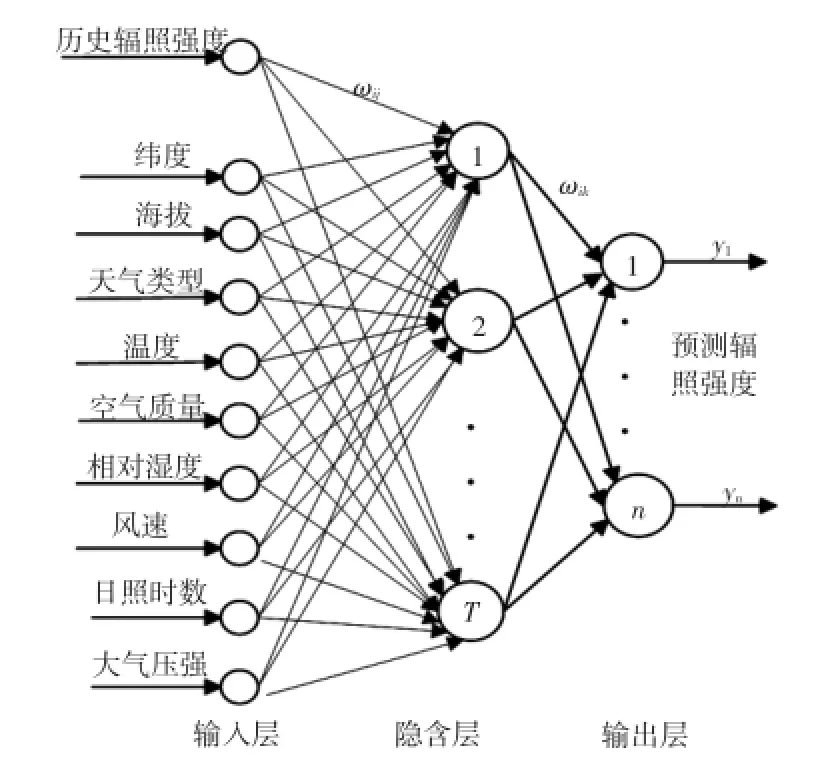
图5 蚁群改进BP神经网络结构Fig.5 Structure of ant colony improved BP neural network

3.3 蚁群算法对改进BP神经网络的训练

若已确定的BP神经网络结构中共有n个权值和阈值，将权值和阈值进行编号处理为ω1，ω2，…，ωn，将ωi（1≤i≤n）分别设置m个非零随机值，从而形成集合Lωi（1≤i≤n）。如果蚁群中有Z只蚂蚁离开蚁穴出去寻找食物，则τj（Lωi）为集合Lωi中第j个元素的信息素。每只蚂蚁根据Lωi的信息状态从中选择一个元素，并调节这个元素的信息素。信息素的计算公式为

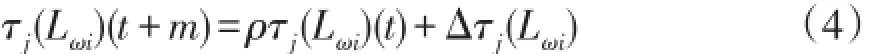
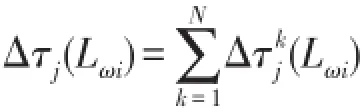
式中：ρ为残留信息的持久度；Δτjk（Lωi）为第k只蚂蚁一次循环在集合Lωi上第j个元素上留下的信息素；τj（Lωi）（t+m）为t+m时刻在集合Lωi上第j个元素的信息素。

由此可知第k只蚂蚁选择集合Lωi上第j个元素的信息素状态转移概率为

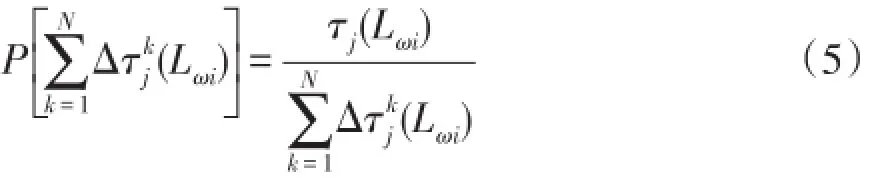
当所有的Z只蚂蚁在Lωi中都选择了一个元素，到达食物源，即完成了在BP神经网络中选择了一组权值和阈值。然后蚂蚁再原路返回到蚁穴，同时优化调节蚂蚁所选的元素的信息素，反复迭代过程中找到全局最优解。本文蚁群改进BP神经网络算法的流程如图6所示。

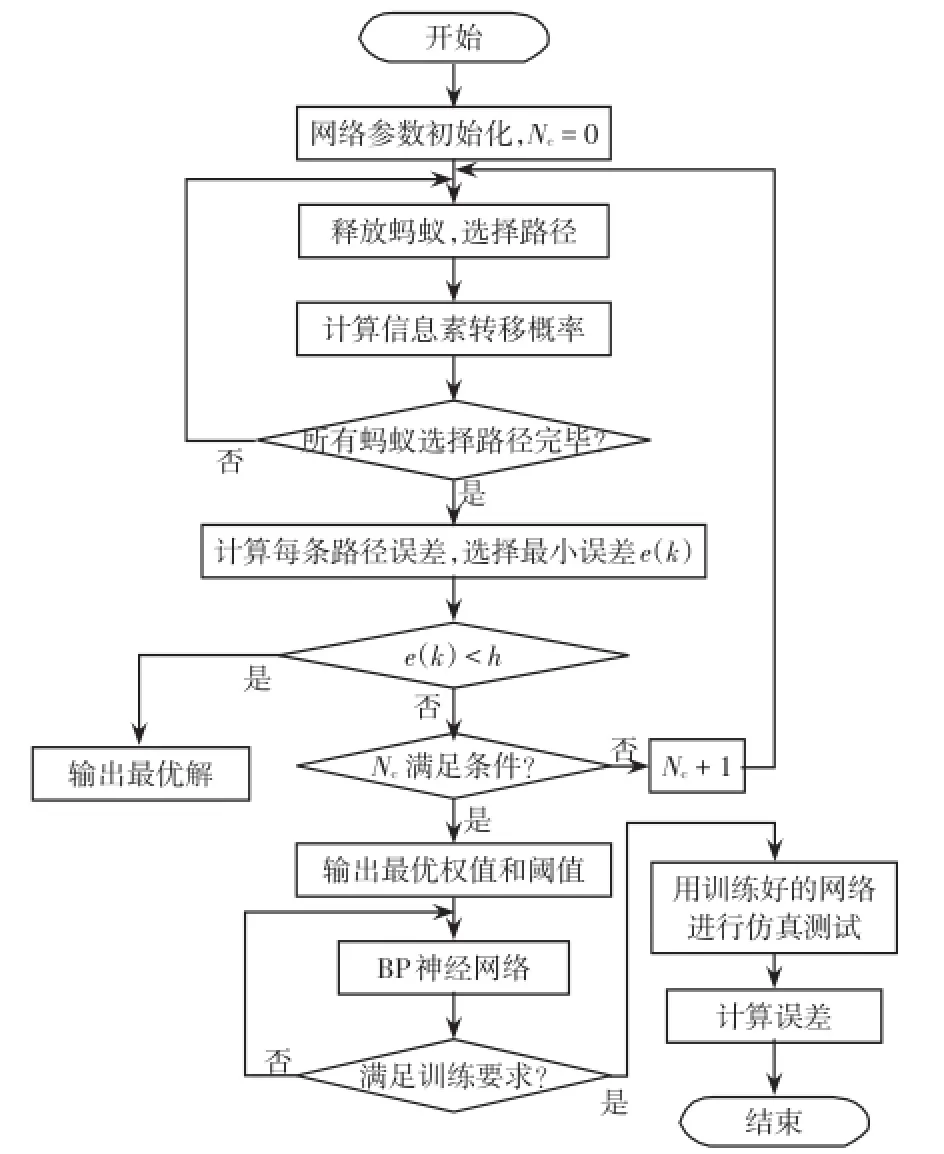
图6 蚁群改进BP神经网络算法流程Fig.6 Flow chart of ant colony improved BP neural network algorithm

4 算例验证

4.1 预测结果分析

本文历史辐照强度、气象因素由宁夏石嘴山第四光伏发电站提供，其位于东经106°59′，北纬39°11′上，海拔高度为1 110 m～1 125 m，总装机容量为30MWp，并网电压为35 kV，发电单元个数为13 200个。

2012年7月1日—2014年8月1日的完整辐照强度相近，温度、日照时数、大气压强等因素变化差异也很小，本文采用按月份分类方法对辐照强度进行预测，共12个预测模型。这种分类方法大大减少了运算量和信息的冗余，提高训练速度。模型分别对2013年11月25日、2014年1月31日、2014年4 月17日、2014年7月2日的辐照强度进行预测，预测时间尺度15 min。预测结果如图7所示。

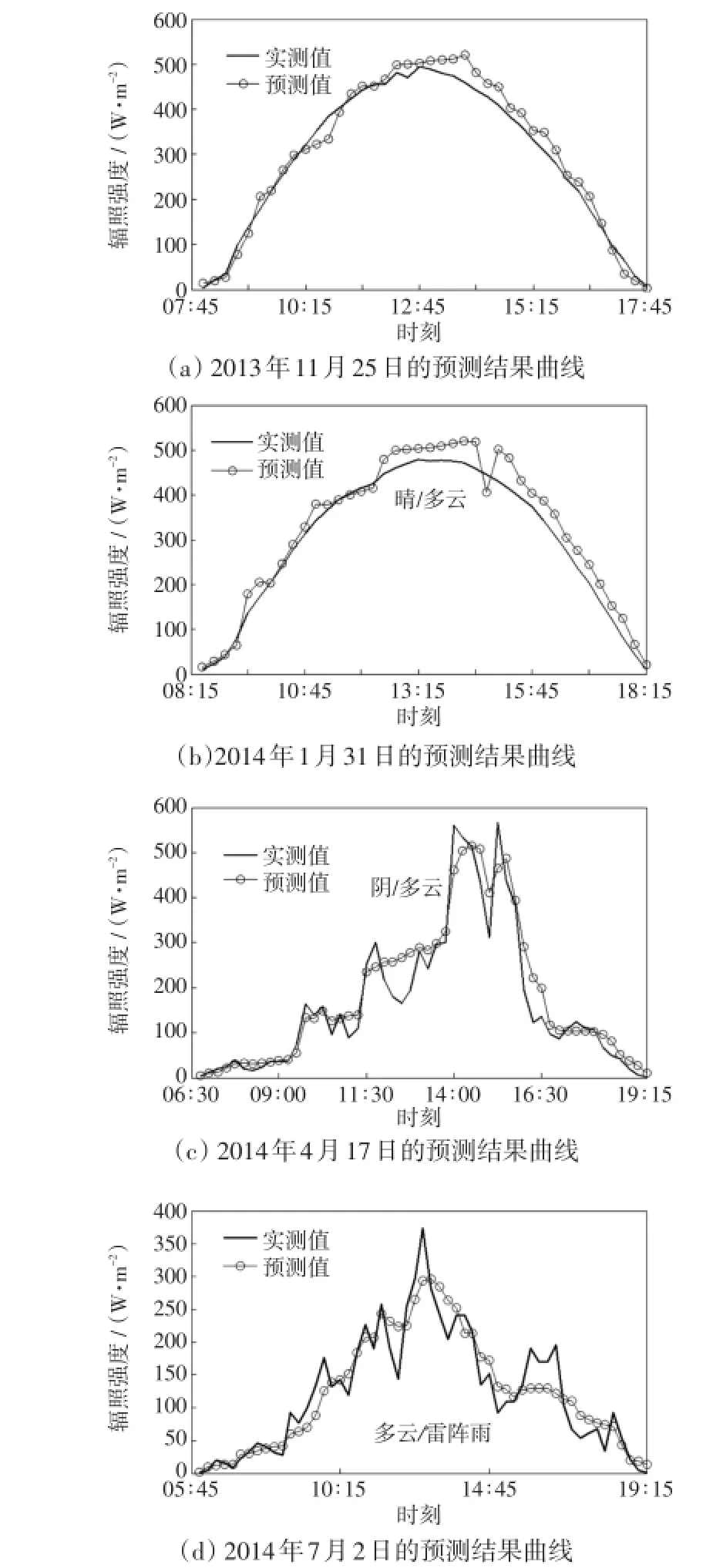
图7 预测结果曲线Fig.7 Curves of predicted results

图7（a）是2013年11月25日的辐照强度的实测值和预测值，把2012年11月份和2013年11月 1—24日的历史辐照强度、纬度、海拔、每天的天气类型（49种的一种）、最高温度、最低温度、空气质量指数、平均相对湿度、平均风速、日照时数、大气压强作为1月份模型的输入量，其中历史辐照强度数据1 620个，影响辐照强度的因素共486个，共1 620个数据对神经网络进行训练。对2013年11月25日的辐照强度进行预测，天气晴，最高温度6℃，最低气温-1℃，空气质量指数35，平均风速3.147 65 m/s，平均相对湿度35.827 04%，日照时数9.75 h，大气压强88.05 kPa，经过反复训练，蚁群参数选为ρ=0.7，蚂蚁数量为32，信息强度为54，最优隐含层数为10个。由图7（a）可知，晴天的预测值与实测值相吻合，预测效果很好。图7（b）是2014年1月31日的辐照强度的实测值和预测值，当天的天气为晴/多云，最高温度11℃，最低气温-6℃，空气质量指数57，平均相对湿度25.433 79%，日照时数9.75 h，平均风速2.250 56 m/s，大气压强90.09 kPa，把历史辐照强度和影响因素共1 654个数据作为输入对1月份神经网络进行训练，经过反复训练，蚁群参数选为ρ=0.6，蚂蚁数量为32，信息强度为41，最优隐含层数为11个，预测取得良好的效果。图7（c）是2014年4月17日的辐照强度的实测值和预测值，当天的天气为阴/多云，最高温度15℃，最低气温8℃，空气质量指数67，平均风速1.774 57 m/s，平均相对湿度31.907 21%，日照时数12.75 h，大气压强93.48 kPa，把历史辐照强度和影响因素共2 817个数据作为输入对神经网络进行训练，蚁群参数选为ρ=0.8，蚂蚁数量为51，信息强度为76，最优隐含层数为10个。由图7（c）可知，阴/多云的天气类型辐照强度随机变化，没有规律可循，预测值与实测值也很接近，在一定程度上达到工程要求。图7（d）是2014年7月2日的辐照强度的实测值和预测值，当天的天气为多云/雷阵雨，最高温度32℃，最低气温19℃，空气质量指数38，平均相对湿度40.69%，平均风速5.998 54 m/s，日照时数5 h，大气压强96.42 kPa，把历史辐照强度和影响因素共3 968个数据作为输入对7月份神经网络进行训练，蚁群参数选为ρ=0.7，蚂蚁数量为54，信息强度为32，最优隐含层数为12个，预测曲线和实测曲线趋势一致，误差在较小的范围内。

上述预测结果表明，按月份分类的预测方法是合理的，在不同天气类型下的预测结果都有较好的预测精度。个别预测点误差大些，这可能因为在采集数据中，由于测量仪器误差因素，导致了实测数据包含一些坏点，天气类型的随机性及不确定性，使得预测结果不准确。但是总体上预测值与实测值很接近。

4.2 与BP神经网络模型的RMSE对比

对预测模型的结果进行估计，本文采用均方根误差RMSE，即

式中，n为网络的输出个数。

基于蚁群改进BP神经网络模型对辐照强度进行预测，上述4天的预测结果与BP神经网络模型预测结果进行对比，表明蚁群改进BP神经网络模型有效提高了特殊天气类型的预测精度。RMSE对比结果如表2所示。

表2 RMSE对比结果Tab.2 Comparison results of RMSE values %

5 结语

本文针对辐照强度的随机性、间歇性、非线性等特点，按月份建立蚁群改进BP神经网络模型预测光伏电站的辐照强度，设计了模型的传递函数、最优输入变量及隐含层的确定方法，克服了神经网络难以确定隐含层数的困难。同时对常见天气类型细致划分为49种，解决了特殊天气类型模糊预测的问题。预测结果证明了按月份建立的蚁群改进BP神经网络预测模型的可行性与准确性。

参考文献：

［1］ Hiyama T，Kitabayashi K.Neural network based estima⁃tion of maximum power generation from PV module using environmental information［J］.IEEE Trans on Energy Con⁃version，1997，12（3）：241-247．

［2］陈刚，袁越，傅质馨（Chen Gang，Yuan Yue，Fu Zhixin）.储能电池平抑光伏发电波动的应用（Application of stor⁃age battery to restrain the photovoltaic power fluctuation）［J］.电力系统及其自动化学报（Proceedings of the CSUEPSA），2014，26（2）：27-31，49.

［3］丁明，王磊，毕月（Ding Ming，Wang Lei，Bi Yue）.基于改进BP神经网络的光伏发电系统输出功率短期预测模型（A short-term prediction model to forecast output power of photovoltaic system based on improved BP neu⁃ralnetwork）［J］.电力系统保护与控制（Power System Protection and Control），2012，40（11）：93-99，148.

［4］Mao P L，Aggarwal R K.A novel approach to the classifi⁃cation of the transient phenomena in power transformers using combined wavelet transform and neural network［J］.IEEE Trans on Power Delivery，2001，16（4）：654-660．

［5］Perez L G，Flechsig A J，Meador J L，et al.Training an arti⁃ficial neural network to discriminate between magnetizing inrush and internal faults［J］.IEEE Trans on Power Deliv⁃ery，1994，9（1）：434-441．

［6］Bastard P，Meunier M，Regal H.Neural network-based al⁃gorithm for power transformer differential relays［J］.IEE Proceedings-Generation，Transmission and Distribution，1995，142（4）：386-392．

［7］代倩，段善旭，蔡涛，等（Dai Qian，Duan Shanxu，Cai Tao，et al）.基于天气类型聚类识别的光伏系统短期无辐照度发电预测模型研究（Short term PV generation system forecasting model without irradiation based on weather type clustering）［J］.中国电机工程学报（Proceedings of the CSEE），2011，31（34）：28-35.

［8］严干贵，王东，杨茂，等（Yan Gangui，Wang Dong，Yang Mao，et al）.两种风电功率多步预测方式的分析及评价（The analysis and evaluation of two ways for multi-step wind power prediction）［J］.东北电力大学学报（Journal of Northeast Dianli University），2013，33（1-2）：126-130.

［9］Bates J M，Granger C.The combination of forecast［J］.Oper⁃ation Research Quarterly，1969，20：451-456.

［10］Dorigo M，Maniezzo V，Colorni A.Ant system：optimiza⁃tion by a colony of cooperating agents［J］.IEEE Trans on Systems，Man and Cybernetics，1996，26（1）：29-41.

［11］Abachizadeh M，Tahani M.An ant colony optimization ap⁃proach to multi-objective optimal design of symmetric hy⁃brid laminates for maximum fundamental frequency and minimum cost［J］.Structural and Multidisciplinary Optimi⁃zation，2009，37（4）：367-376．

贺 文（1973—），男，博士，高级工程师，研究方向为电网调度运行。Email：yqdhqs0611@126.com

齐 爽（1989—），女，通讯作者，硕士研究生，研究方向为光伏并网发电系统。Email：719620760@qq.com

陈厚合（1978—），男，博士，副教授，研究方向为电力系统安全性与稳定性分析。Email：chenhouhe@gmail.com

中图分类号：TM615

文献标志码：A

文章编号：1003-8930（2016）07-0026-06

DOI：10.3969/j.issn.1003-8930.2016.07.005

作者简介：

收稿日期：2015-03-24；修回日期：2015-12-28

基金项目：国家自然科学基金资助项目（51377016）；长江学者和创新团队发展计划资助项目（IRT1114）；吉林省科技发展计划资助项目（20140101080JC）

Prediction of Radiation Intensity for Photovoltaic Power Plants Based on Ant Colony BP Neural Network

HE Wen1，QI Shuang2，CHEN Houhe2
（1.State Grid of Ningxia Electric Power Company，Yinchuan 750001，China；2.Electrical Engineering College，Northeast Dianli University，Jilin 132012，China）

Abstract：In order to improve the prediction accuracy of radiation intensity in photovoltaic power plants，this paper pro⁃poses a predicted method based on ant colony BP neural network.Firstly，the influencing factors are analyzed，and the optimal factors are selected as the inputs of the model，including latitude，altitude，weather type，sunshine hours，tem⁃perature，air quality，relative humidity，wind speed，atmospheric pressure.Secondly，a new transfer function is estab⁃lished，and the number of hidden layers is automatically optimized by the minimum mean square error energy function.At last，twelve ant colony BP network models are established by month to predict the radiation intensity.According to the comparison of predicted results between the proposed method and BP neural network model，it is proved that the prediction accuracy is effectively improved.

Key words：photovoltaicpowerplant；radiationintensity；antcolonyalgorithm；improvedBPneuralnetwork；prediction