双馈感应风力发电机并网的复合电能质量检测方法

李文慧，刘志刚，崔 艳（西南交通大学电气工程学院，成都 610031）

双馈感应风力发电机并网的复合电能质量检测方法

李文慧，刘志刚，崔 艳
（西南交通大学电气工程学院，成都 610031）

摘要：风电并网引起的电能质量扰动信号多为复合的暂态振荡信号，针对传统的检测算法存在模态混叠、易受干扰、通用性差等缺点，提出采用聚类经验模态分解EEMD与基于Morlet复小波的谱峭度相结合的算法实现该类扰动检测。为采集风电并网引起的相关电能质量扰动信号，在实时数字仿真RTDS平台搭建了200台双馈感应风力发电机DFIG的风电场并网模型。仿真结果表明，该算法能有效实现对风电并网引起的电能质量复合扰动信号的检测。

关键词：风电并网；电能质量；复合扰动；EEMD；Morlet复小波；谱峭度；实时数字仿真

近年来，风能作为一种清洁环保的新能源被广泛应用，然而由于风具有波动性、随机性等特点，使得大规模风电并网对电力系统电能质量产生影响［1-2］。双馈感应风力发电机DFIG（doubly-fed in⁃duction generator）采用变桨距控制，比定桨距失速型风机具有更高的风能利用率，且在变速运行时可以发出频率恒定的电能，逐步成为兆瓦级风电机组的主流机型［3-4］，因此，研究DFIG并网对电能质量的影响具有重要现实意义。

迄今为止，国内外已有大量电能质量分析算法：文献［5］利用小波包和Tsallis奇异熵检测暂态电能质量扰动；文献［6］在局部均值分解LMD（local mean decomposition）的基础上提出一种改进的LMD电能质量扰动检测方法；文献［7］运用基于巴特沃斯分布BWD（Butterworth distribution），谱峭度结合支持向量机实现暂态电能质量扰动识别；文献［8］用改进的Hilbert-Huang变换进行电能质量扰动信号的时频分析。然而上述方法大多针对Matlab产生的理想扰动信号，不适合风电并网产生的含有暂态振荡的复合扰动。文献［9］利用聚类经验模态分解EEMD（ensemble empirical mode decomposition）分解出信号中存在的不同谐波频率成分，结合Hilbert变换得到瞬时频率，但这种方法无法得到信号频率累积信息；文献［10］基于Morlet小波的谱峭度算法检测含噪信号中的瞬态成分，能够得到信号频域累积量，但是不能反映时域信息，不能检测幅值类扰动的扰动幅值和持续时间。

本文将EEMD与基于Morlet小波的谱峭度算法结合，解决了两种算法各自的缺点，使分析结果不仅能反映信号的时域特性，还能得到信号的频域累积量。此外，文中在实时数字仿真RTDS（real time digital simulator）平台上搭建风电场并网模型，采集相关电能质量扰动信号数据，仿真结果接近实际，且避免了风电场实测信号数据采集困难的问题，然后对该类信号进行了仿真分析，验证了本文方法的有效性。

1 DFIG并网电能质量扰动检测算法

1.1 EEMD方法

经验模态分解EMD（empirical mode decomposi⁃tion）方法能把原始的扰动信号分解成为若干频率由高到低排列的本征模态函数IMF（intrinsic mode function）和一个残余量。但由于风电并网产生的扰动信号不是纯噪声信号，会缺失一些频率尺度，所以容易出现模态混叠现象。文献［11］对EMD分解白噪声的统计特性进行研究，巧妙地运用了白噪声频率均匀分布的统计特性，将其应用到EMD中，这就是EEMD的方法。

1）EMD原理

EMD方法是将原始扰动信号分解为若干IMF的过程，IMF有以下两个特点：①IMF极值点和过零点点数必须相等或相差为1；②IMF上任意点都需满足局部极大值点定义的上包络线和局部极小值点定义的下包络线均值为0。具体的分解步骤如下。

（1）假设原始扰动信号为s（t），求出局部极大值和极小值，并用三次样条线分别将所有局部极大值和所有局部极小值连接起来，形成上、下包络线v1（t）、v2（t），上、下包络线将原始信号包在中间，求出平均值m1为

然后将s（t）与m1相减记为h1，则有

（2）如果不满足IMF两个条件，就将h1看作原始信号，重复步骤（1），直到h1满足IMF条件。最终的IMF分量是多个h1叠加后平均的结果，设为c1。

（3）s（t）中分解出c1后，得到剩余信号r1为

将r1看作原始信号重复上述两个步骤，得到原始信号的第2个IMF分量c2，直到残余信号单调，不能再分出新的IMF，最后的残余信号为rn。因此，原始扰动信号可以由IMF分量和残余信号重构，即

2）EEMD原理

EEMD方法就是首先添加均值为0，幅值标准差为常数（一般取原信号标准差的0.1～0.4）的白噪声，使得被分解的信号在不同程度上有一定连续性，从而避免模态混叠现象。然后进行上述EMD分解，得出IMF，EEMD分解流程见图1，分解步骤如下。

（1）在原扰动信号s（t）添加高斯白噪声w（t），得到含噪声信号x（t）为

（2）运用EMD方法将x（t）分解得到一组IMF（假设共有n个分量），即

（3）在s（t）中添加新的高斯白噪声wi（t）（i=1，2，…，N）再进行EMD分解，即重复上述两个步骤N次，即

（4）将N次分解得到的IMF分量做均值（此处利用高斯白噪声零均值的原理消除白噪声对原信号的影响），得到最终的IMF，即

图1 EEMD算法流程Fig.1 Flow chart of EEMD algorithm

1.2 基于Morlet复小波的谱峭度算法

DFIG中电力电子器件的大量使用，风机启动、切除，风机故障等，会引起风电并网产生的扰动信号中出现振荡暂态。谱峭度是在谱分析和峭度分析的基础上发展而来，能够用来检测信号中的瞬态成分，适合检测暂态振荡的扰动频率。选用基于小波变换的谱峭度，主要是因为这种谱峭度时频域局部化性能好，其尺度变换刚好能够满足暂态振荡信号频率检测的需要［12-13］。Morlet复小波是一种连续复小波，其基小波定义为复指数函数与高斯函数的乘积，采用的Gauss窗是时-频面积最小的窗函数，变换结果可同时反映信号的幅值和相位关系［14］。

用φa，b（t）表示尺度参数为a、平移参数为b的Morlet小波，用WTs（a，b）表示扰动信号s（t）的连续小波变换，以Morlet复小波函数为母函数的小波变换表示为

根据谱峭度的定义［15］，基于小波变换的谱峭度计算公式为

式中E为均值运算。

图2 风电并网电能质量扰动检测流程Fig.2 Flow chart of wind power grid power quality disturbance detection algorithm

1.3 EEMD与Morlet复小波谱峭度结合检测

本文将EEMD与基于Morlet复小波的谱峭度算法相结合，对DFIG并网产生的扰动信号进行检测，检测流程如图2所示。图中x为暂态振荡模态的IMF个数，求和得到最终的暂态振荡模态IMF_ot；y为幅值类扰动的IMF个数，求和得到最终的幅值类模态IMF_am；f1，f2，……，fm为检测出的暂态振荡频率；A为扰动幅值；t为检测出的扰动持续时间。

风电并网电能质量扰动检测算法步骤如下：

（1）输入待检测DFIG并网信号，并对其进行EEMD分解得n个IMF分量；

（2）根据式（10）求出扰动分量的谱峭度值，画出曲线图，再根据暂态振荡信号谱峭度明显波峰的特点，区分暂态振荡模态和幅值类扰动模态；

The lattice distance (d), average crystalline grain size(D), and strain (ε) of the (001) plane are given by the following equations[40]:

（3）对幅值类扰动分量运用文献［16］的方法进行Hilbert变换，得到其瞬时幅值和瞬时频率，实现扰动幅值和扰动时间的检测；

（4）对于暂态振荡分量，计算基于Morlet复小波的谱峭度，得到谱峭度图，实现振荡频率的检测。

1.4 算法的仿真验证

DFIG并网引起的电能质量扰动信号多为复合的暂态振荡信号，本节将验证本文提出的算法应用于算法产生的此类信号的有效性。用Matlab产生电压暂降和暂态振荡的复合扰动信号对本文提出的算法进行验证。暂态振荡数学模型为

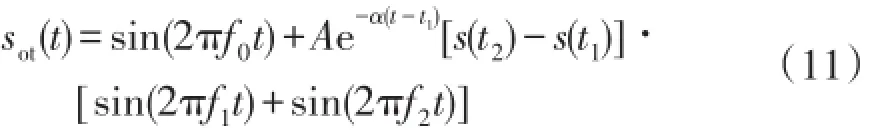
电压暂降数学模型为

复合扰动信号为

图3 暂态振荡加电压暂降EMD结果Fig.3 EMD results of transient oscillation and voltage interrupt

利用式（13），产生基频为50 Hz，电压暂降和暂态振荡复合，振荡频率为1 kHz和2 kHz叠加的复合扰动信号。图3为该信号EMD分解情况，图中s（t）为原始复合扰动信号，子图IMF1～IMF4为EMD分解得到的IMF分量，可见出现了严重的模态混叠，不能将两种扰动分解开。图4为电压暂降加暂态振荡信号EEMD分解结果，图中s（t）为原始复合扰动信号，子图IMF1～IMF4为EEMD分解得到的IMF分量，由图可知可以有效地将振荡模态和暂降模态分解开，避免了模态混叠现象。图5为运用基于Morlet复小波的谱峭度算法对IMF进行模态识别的结果，可见IMF2和IMF3分别表征频率为2 kHz 和3 kHz的暂态振荡模态，IMF4表征的是电压暂降模态。图6（a）和（b）分别是将原信号直接进行谱峭度计算的结果和将暂态振荡分量进行谱峭度计算的结果，可以看出将原信号直接进行谱峭度计算不能很好地检测出暂态振荡频率，而本文的方法很好地解决了谱峭度方法用于复合扰动检测失效的问题。

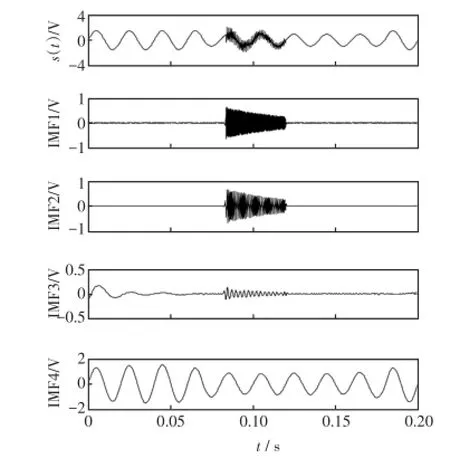
图4 暂态振荡加电压暂降EEMD结果Fig.4 EEMD results of transient oscillation and voltage interrupt

图5 基于Morlet复小波的谱峭度进行模态识别Fig.5 Model identification of Morlet complex wavelet based spectral kurtosis

图6 原信号和暂态振荡分量进行谱峭度运算结果对比Fig.6 Comparative analysis of spectral kurtosis of original signal and transient oscillation component

2 DFIG并网模型的搭建

相较于非实时仿真方式，实时数字仿真方式具有响应时间更短，可在一个仿真步长内实现实际电力系统在该时间内的动态响应；能模拟一定规模的电磁暂态、机电暂态过程等优点。故本文基于RTDS平台搭建了DFIG并网模型。

RTDS的图形用户界面为RSCAD，本文运用RSCAD建立DFIG并网模型，并结合RTDS硬件运行得到相关数据，进行研究。

2.2 DFIG并网原理

DFIG并网时，定子侧的三相绕组直接接入电网，转子三相绕组经变换器接入电网［17］，变换器根据风机的不同运行状态实现整流或逆变功能，图7为具体模型结构和连接原理。

图7 模型结构和连接原理Fig.7 Model structure and connection principle

2.3 DFIG并网模型

本文搭建一个含200台DFIG的风电场，DFIG参数见表1。风电场模型通过升压变压器接入7节点的电力系统实现并网运行，图8为风电场并网示意，图9为7节点电力系统连接示意，其中1号节点充当系统的平衡节点，5号节点接入额定功率为250 MW的其他动力发电机，7号节点接入风力发电机组，系统中3段输电线路长度均为100 km。

表1 DFIG参数Tab.1 DFIG parameters

图8 风电场并网示意Fig.8 Schematics diagram of wind farm grid

图9 IEEE-7节点电力系统连接示意Fig.9 Connection diagram of IEEE 7-node system

3 DFIG并网短路故障的电能质量扰动仿真分析

风机运行在设定的额定风速（12 m/s）下，在风机出口处设置持续时间为0.1 s的三相接地短路故障，在额定风速为12 m/s、采样频率为18 182 Hz，采样点数为18 182的条件下，以节点2为例，对包含整个故障持续过程的前5 000个数据点进行分析。图10为节点2某相电压信号EEMD分解结果，其中图10（a）为原始信号，图10（b）为表征暂态振荡模态的IMF叠加结果，与图4理论信号的EEMD分解结果对比可以发现，实时仿真信号中暂态振荡模态往往在暂降扰动的起始时间点和终止时间点出现，这给此类问题的检测带来困难。图11为图10（b）中的振荡模态分量基于Morlet复小波的谱峭度，可见本文提出的方法适合于应用在实时仿真中。

图10 节点2某相电压信号EEMD分解结果Fig.10 EEMD of one phase voltage signal in Node 2

图11 节点2暂态振荡分量基于Morlet复小波的谱峭度Fig.11 Morlet complex wavelet based spectral kurtosis of transient oscillation component in Node 2

表2 电压暂降检测结果Tab.2 Detection results of voltage sag

表3 暂态振荡检测结果Tab.3 Detection results of transient oscillation

表2和表3是对图9中各节点的检测结果统计，分别为电压暂降和暂态振荡的检测结果。从表2可以看出，靠近风电机组并网点的节点暂降幅度较大，远离并网点的节点暂降幅度较小，并且将检测的结果与RTDS仿真模型中设置的短路故障持续时间对比，可见误差较小，检测结果较可靠；从表3可以看出，从靠近并网点的节点中可以检测到较多的振荡频率分量，从远离并网点的节点中检测到的振荡频率分量较少。因此，风机短路故障对接入电力系统节点的电能质量影响的具体表现为：对靠近风电机组并网点的节点影响较大，对远离风电机组并网点的节点影响较小。

4 结语

本文提出了EEMD和基于Morlet复小波的谱峭度相结合的算法，在RTDS平台搭建了200台DFIG风电场并网模型，采集风机出口处故障产生的电能质量扰动信号，并进行检测。本文提出的算法实现了对风电并网引起的暂态振荡频率、幅值类扰动的扰动持续时间和扰动幅值的检测，并得出，在风电机组并网节点引起的电能质量扰动最明显，靠近并网节点的扰动比远离并网节点的扰动明显，与理论相符。通过本算法检测到的与设置的故障持续时间对比可知，本算法检测效果较好，误差较低。

参考文献：

［1］张国新（Zhang Guoxin）.风力发电并网技术及电能质量控制策略（Parallel-in technology of wind power and pow⁃er quality control strategy）［J］.电力自动化设备（Electric Power Automation Equipment），2009，29（6）：130-133．

［2］刘桂英，粟时平（Liu Guiying，Su Shiping）.风电接入系统的暂态电能质量扰动小波检测方法（Wavelet detec⁃tion method of transient power quality disturbance for power system connected with energy generation）［J］.电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（1）：22-27．

［3］ 马越，陈星莺，余昆，等（Ma Yue，Chen Xingying，Yu Kun，et al）.不同类型短路故障下双馈风机短路电流分析（Analysis for short circuit current of DFIG-based wind generation system under different types of short circuit）［J］.电力系统及其自动化学报（Proceedings of the CSU-EP⁃SA），2014，26（2）：60-65．

［4］周羽生，郑剑武，向军，等（Zhou Yusheng，Zheng Jianwu，Xiang Jun，et al）.双馈风力发电系统网侧变流器联合控制策略（Combination control strategy for grid convert in doubly-fed wind power generation systems）［J］.电力系统及其自动化学报（Proceedings of the CSU-EPSA），2014，26（4）：25-29．

［5］Liu Zhigang，Hu Qiaoling，Cui Yan，et al.A new detec⁃tion approach of transient disturbances combining wavelet packet and Tsallis entropy［J］.Neurocomputing，2014，142 （142）：393-407．

［6］宋海军，黄传金，刘宏超，等（Song Haijun，Huang Chuan⁃jin，Liu Hongchao，et al）.基于改进LMD的电能质量扰动检测新方法（A new power quality disturbance detec⁃tion method based on the improved LMD）［J］.中国电机工程学报（Proceedings of the CSEE），2014，34（10）：1700-1708．

［7］陈刚，刘志刚，张巧革（Chen Gang，Liu Zhigang，Zhang Qiaoge）.基于BWD谱峭度的暂态电能质量扰动分类识别（Classification of transient power quality disturbanc⁃es based on BWD spectral kurtosis）［J］.电力系统及其自动化学报（Proceedings of the CSU-EPSA），2014，26（7）：11-16．

［8］ Senroy N，Suryanarayanan S，Ribeiro P F.An improved Hilbert-Huang method for analysis of time-varying wave⁃forms in power quality［J］.IEEE Trans on Power Systems，2007，22（4）：1843-1850．

［9］朱宁辉，白晓民，董伟杰（Zhu Ninghui，Bai Xiaomin，Dong Weijie）.基于EEMD的谐波检测方法（Harmonic detection method based on EEMD）［J］.中国电机工程学报（Proceedings of the CSEE），2013，33（7）：92-99．

［10］Liu Haiyang，Huang Weiguo，Wang Shibin，et al.Adaptive spectral kurtosis filtering based on Morlet wavelet and its application for signal transients detection［J］.Signal Pro⁃cessing，2014（96）：118-124．

［11］张杨，刘志刚（Zhang Yang，Liu Zhigang）.EEMD在电能质量扰动检测中的应用（Application of EEMD in power quality disturbance detection）［J］.电力自动化设备（Elec⁃tric Power Automation Equipment），2011，31（12）：86-91.

［12］Liu Zhigang，Zhang Qiaoge.An approach to recognize the transient disturbances with spectral kurtosis［J］.IEEE Trans on Instrumentation and Measurement，2014，63（1）：46-55．

［13］张巧革，刘志刚，陈刚（Zhang Qiaoge，Liu Zhigang，Chen Gang）.暂态振荡信号频率检测的Morlet小波谱峭度法（Frequency detection of transient oscillation signal using Morlet wavelet based on spectral kurtosis method）［J］.电力系统及其自动化学报（Proceedings of the CSU-EP⁃SA），2013，25（5）：1-6．

［14］揭林玲，唐昆明，张太勤（Jie Linling，Tang Kunming，Zhang Taiqin）.Morlet复小波算法在自适应电流保护中的应用研究（Study on application of Morlet complex wavelet on adaptive current protection）［J］.电力系统保护与控制（Power System Protection and Control），2009，37 （22）：40-43，48.

［15］Antoni J.The spectral kurtosis：a useful tool for character⁃ising non-stationary signals［J］.Mechanical Systems and Signal Processing，2006，20（2）：282-307．

［16］刘志刚，李文帆，孙婉璐（Liu Zhigang，Li Wenfan，Sun Wanlu）.Hilbert-Huang变换及其在电力系统中的应用（Hilbert-Huang transform and its applications in power system）［J］.电力自动化设备（Electric Power Automation Equipment），2012，32（4）：109-116.

［17］Zin A A B M，Mahmoud P H A，Khkairuddin A B，et al．An over view on doubly fed induction generators’controls and contributions to wind based electricity generation［J］.Renewable and Sustainable Energy Reviews，2013，27 （27）：692-708．

李文慧（1991—），女，硕士研究生，研究方向为现代信号处理技术及其在电力系统中的应用。Email：wh_venny@163.com

刘志刚（1975—），男，博士，教授，博士生导师，研究方向为现代信号处理技术及其在电力系统中的应用、轨道交通电气化自动化技术。Email：liuzg_cd@126.com

崔 艳（1991—），女，硕士研究生，研究方向为现代信号处理理论及其在电力系统中的应用。Email：cy_kuaile123@126.com

中图分类号：TM712

文献标志码：A

文章编号：1003-8930（2016）07-0001-06

DOI：10.3969/j.issn.1003-8930.2016.07.001

作者简介：

收稿日期：2015-01-30；修回日期：2016-01-08

基金项目：国家自然科学基金资助项目（U1434203、U1134205、51377136）

A Multiple Power Quality Detection Method for Disturbances of DFIGs Grid

LI Wenhui，LIU Zhigang，CUI Yan
（School of Electrical Engineering，Southwest Jiaotong University，Chengdu 610031，China）

Abstract：The power quality disturbances caused by wind power grid are mostly multiple disturbances including tran⁃sient oscillation.According to the disadvantages of traditional detection methods，such as modal aliasing，susceptibility to disturbance and poor universality.An algorithm of ensemble empirical mode decomposition（EEMD）combined with Morlet complex wavelet based spectral kurtosis（SK）is proposed to detect these kinds of power quality disturbances in this paper.The wind farm model of 200 doubly-fed induction generators（DFIGs）is built on the platform of real time dig⁃ital simulator（RTDS）to collect power quality disturbance signals related to wind power grid.The simulation results show that the method can effectively detect the multiple power quality disturbances caused by wind power grid.

Key words：wind power grid；power quality；multiple disturbances；ensemble empirical mode decomposition （EEMD）；Morlet complex wavelet；spectral kurtosis；real time digital simulator