频谱重叠因子对数字调制系统的性能影响分析
郭黎利,李清伟,戴佳,刘湘蒲
(哈尔滨工程大学 信息与通信工程学院, 黑龙江 哈尔滨 150001)
频谱重叠因子对数字调制系统的性能影响分析
郭黎利,李清伟,戴佳,刘湘蒲
(哈尔滨工程大学 信息与通信工程学院, 黑龙江 哈尔滨 150001)
摘要:一般数字调制系统的性能分析都是在信号、噪声统计规律的基础上,通过时域的数学方法进行的,但针对目前和未来复杂通信环境(如认知无线电系统的授权用户规避、窄带或宽带干扰影响等问题),经典的分析方法尚不能准确、定量的描述数字调制系统的误码率性能。该论文从频域分析的角度出发,提出了频谱重叠因子(spectrum overlap factor, SOF)的概念,推导并修正了干扰存在下经典的2ASK、BPSK和FSK调制方式的误码率公式。在证实直观物理意义的基础上,给出了定量的数学描述。实验仿真结果验证了频域分析的正确性。
关键词:误码率;时域分析;授权用户;频谱重叠因子(SOF);数字调制;频域分析
网络出版地址:http://www.cnki.net/kcms/detail/23.1390.u.20160127.1102.010.html
2ASK、BPSK和2FSK是数字通信系统的基础[1-2]。已有的研究都是给出了3种经典调制方式下的高斯白噪声下的误码率性能,而其干扰存在下的误码率公式却很少给出,并且传统的误码率推导都是考虑了噪声和信号的统计特性从时域进行判决分析的[3-4]。而伴随着通信的发展,日益增多的用户导致通信的频谱资源日益稀缺,实际的通信环境中,对任意当前通信用户来说,空间存在着类似于授权或者认知用户这样的干扰[5-6]。频谱的重叠使得当前用户的通信性能下降。直观的物理概念是,当前用户和其他干扰的频谱重叠越严重,通信性能越差。因此,如果能从频谱重叠的角度去分析通信系统干扰下的误码率性能,能使得推导出来的误码率公式更直接。尤其是,对信号在频域的分析处理方法,本来就是通信中常用的手段[7-9]。为此,本文从干扰与信号频谱重叠的角度考虑分析了数字调制系统(2ASK、BPSK、2FSK)中存在干扰时的误码率性能,把物理概念上的频谱重叠应用于误码率公式的推导中。
1理论推导分析
本节将依次给出BPSK、2ASK和2FSK 3种调制方式下通信系统的抗干扰性能,并经过推导给出了具体的误码率表达式。
1.1BPSK调制干扰存在时的误码率分析
(1)
令T表示离基带信源周期;T0表示载波周期,且T=kT0,T≫T0。通常情况下,对于BPSK调制来说,基带信源波形w(t)采用矩形波。
(2)

Pe=
(3)


图1 BPSK最佳接收机示意图Fig.1 The schematic diagram of optimal receiver with BPSK modulation
1.22ASK调制干扰存在时的误码率分析

(4)
1.32FSK调制干扰存在时的误码率分析
如图 2所示,发送0和1时2FSK采用两载波频率分别是f1和f2,相应的角频率为ω1何ω2。类似于BPSK,同样接收信号x(t)=s(t)+n(t)+i(t)。只不过发送0和1时相应的发射信号s(t)有所不同,与之相应的接收误码推导也不相同,下面分别进行讨论分析。

图2 2FSK最佳接收框图Fig.2 The schematic diagram of optimal receiver with 2FSK modulation
1)发送0码时,s(t)=Acos(ω1t),此时
(5)
(6)

则发送0码时接收端的误码率表示为
(7)
令
(8)

(9)
2)发送1码时,s(t)=Acos(ω2t)
(10)
(11)
同理推导如上,发送1码时接收端的误码率:
(12)
令

(13)
综合1)和2),当发送的0和1等概率时,可得出2FSK相干解调时的误码率表达式为
(14)
综合1.1、1.2 和1.3节3种情况,当采用的信源幅度A=1时,T=2Eb。此时,式(3)、(4)、(14)分别简化如下:
(15)
(16)
(17)
下面将通过推导给出式(15)~(17)中的I(t)的具体物理含义。对于BPSK和2ASK, I(t) 可简化为

(18)
(19)
其中Δω=ωI-ω0。需要注意的是,当干扰属于随机信号时,此时I(t)也属于随机变量,因此需要对式(15)~(17)做进一步的统计平均。因此,针对包含随机相位θ的单频干扰,式(15)~(17)可进一步用通式:
(20)
(21)
(22)

(23)
(24)
(25)
式(23)~(25)都可以归一化为通式:
(26)
对不同的调制方式,只需要令α和k (α>0,k>0)取不同的值即可。
对通式(26)两边对β求导可得
(27)

2试验仿真
试验仿真主要进行了2ASK、BPSK和2FSK 3种数字调制下的理论和实际的误码率性能对比分析。实验仿真共分为3个部分:1)单频干扰下3种调制方式的理论和实际的误码率性能对比分析,2)窄带干扰下3种调制方式的理论和实际的误码率性能对比分析,3)带宽固定中心频率不同时,产生不同的频谱重叠度时3种信源的误码率性能分析。
仿真条件:数字基带的信源符号周期为Td,符号速率fd=1/Td,载波频率为f0。
对于误码率仿真曲线,单频干扰或者窄带干扰下均给出了2ASK、BPSK和2FSK 3种调制方式下的理论和实际的仿真曲线。由于对于理论和实际的接收判决来说,均是针对单个信源符号进行的,因此对于实验仿真部分需要给出的是单个符号周期Td内的接收3种信号分量的频谱图。因此,对于接收机的信源、干扰和噪声的频谱仿真图中,这里只给出了不同中心频率单频干扰下具有代表性的BPSK调制下接收机3种信号分量的频谱图,而对于2ASK和2FSK,单个信源符号内的频谱仿真图类似,不再一一给出。
2.1不同中心频率单频干扰下BPSK调制下接收机的信号分量频谱图
附加条件,仿真中单频干扰1和单频干扰2所采用中心频率分别为f0+0.2fd和f0+0.6fd的单频干扰。仿真结果如图 3所示。

图3 不同中心频率下的信号分量频谱Fig.3 The signal component spectrogram with the tone jamming located in different central frequency
2.2单频干扰下3种经典调制方式的误码率特性对比
附加条件:单频干扰的中心频率为f0+0.2fd,信号与干扰单位比特能量比Eb/EI=12dB。
如图 4所示,分别给出了,单频干扰下2ASK、2FSK和BPSK3种经典调制方式的理论和实际的误码率特性。
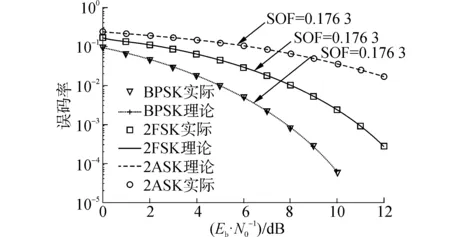
图4 单频干扰中心频率为f0+0.2fd时3种调制方式下的误码率Fig.4 The BER of three modulation systems with the tone jamming located in f0+0.2fd
3种调制方式下,理论和实际曲线重合表明了单频干扰下,误码率理论分析的正确性。同时,给出了3种调制方式下当前干扰下相对应的SOF值。为了更充分的证明理论分析,下面给出了单频干扰中心频率位于f0+0.6fd时的信号接收频谱图和3种调制方式的误码率曲线,相应的Eb/EI同样为12dB。图 5给出了相应的仿真结果。
同图 4类似,图 5的仿真结果表明,当单频干扰的中心频率位于f0+0.6fd时,理论和实际仿真曲线的重合同样证实了理论分析的正确性。

图5 单频干扰中心频率为f0+0.6fd时3种调制方式下的误码率Fig.5 The BER of three modulation systems with the tone jamming located in f0+0.6fd
2.3窄带干扰下3种调制方式的误码率仿真
窄带干扰的频段为f0+0.2~f0+0.6fd,占信源频谱带宽的20%,Eb/EI=18dB。以下给出,窄带干扰下,3种调制方式下的误码率特性对比以及接收机接收到的信源、干扰和噪声3种信号分量的频谱图。
图 6给出了窄带干扰下的最佳接收机下的3种调制方式下的误码率特性。同样可以看出,窄带干扰下,3种经典调制方式的理论BER曲线和实际的BER曲线重合,这同样的证实了窄带干扰下,理论推导的BER公式的正确性。

图6 窄带干扰频段为f0+0.2~f0+0.6fd时3种调制方式下的误码率Fig.6 The BER of three modulation systems with the band jamming located in f0+0.2~f0+0.6fd
为了更直观的给出频谱重叠对于数字基带通信BER性能的影响,下面给出一个带宽固定的宽带信号,随着中心频率的移动,宽带信号与数字基带信号的频谱重叠率改变时,给出相应的仿真结果。 对于频谱重叠率是这样定义的,即直观意义上的干扰和发射信号重叠的频段长度BI与信源带宽长度2fd的比值。
2.4宽带干扰下3种调制方式的误码率仿真
设定一宽带干扰,带宽为fd,随着宽带干扰中心频率的改变,干扰和信源主瓣的频谱重叠率在改变,相应的频谱重叠度和误码率均在改变。为了更直观的验证理论的分析结果,仿真采用3个频谱重叠率分别为50%、25%和0%,Eb/EI=18dB。表1给出3种调制方式相应的仿真SOF值。表1中的仿真结果表明,当宽带干扰逐渐的偏离发射信号的中心旁瓣时,重叠率降低,此时的SOF值也降低,误码率性能也随之变好。

表1 不同重叠率下3种调制方式的SOF仿真值
3结论
1)给出了干扰存在时,2ASK、BPSK和2FSK 3种调制方式下数字基带系统的误码率公式。
2)提出了频谱重叠因子(SOF)的概念,并给出了BER和SOF的数学表达式关系,并推导分析论证了BER是SOF的递增函数。
3)实验仿真证实了频域分析在数字调制系统误码率性能分析的正确性。相对于以往对调制系统从时域进行的误码率推导分析,本文从频域的角度着手,把直观的频谱重叠概念与实际通信系统的性能建立了数学上的关系式,从而为信源的频谱设计提供了更直观有效的设计准则,也便于分析干扰情况下的通信系统性能。
参考文献:
[1]SKLAR B. 数字通信: 基础与应用[M]. 徐平平, 宋铁成, 叶芝慧, 等译. 2版. 北京: 电子工业出版社, 2002: 129-134.
[2]樊昌信, 曹丽娜. 通信原理[M]. 6版. 北京: 国防工业出版社, 2006: 180-212.
[3]郭黎利, 刘湘蒲, 付江志, 等. 基于块编码的功率谱可控复合序列[J]. 哈尔滨工程大学学报, 2015, 36(2): 248-251, 256.
GUO Lili, LIU Xiangpu, FU Jiangzhi, et al. Controllable composite sequence of power spectral density based on the block coded signal[J]. Journal of Harbin Engineering University, 2015, 36(2): 248-251, 256.
[4]KIM K S, MAROM D M, MILSTEIN L B, et al. Hybrid pulse position modulation/ultrashort light pulse code-division multiple-access systems. I. Fundamental analysis[J]. IEEE transactions on communications, 2002, 50(12): 2018-2031.
[5]LIN Y E, LIU K H, HSIEH H Y. On using interference-aware spectrum sensing for dynamic spectrum access in cognitive radio networks[J]. IEEE transactions on mobile computing, 2013, 12(3): 461-474.
[6]ZHANG Shibing, DONG Xiaodai, BAO Zhihua, et al. Adaptive spectrum sensing algorithm in cognitive ultra-wideband systems[J]. Wireless personal communications, 2013, 68(3): 789-810.
[7]褚振勇, 易克初, 田红心. 直接序列扩频信号的时频特性分析[J]. 电路与系统学报, 2004, 9(3): 23-28.
CHU Zhenyong, YI Kechu, TIAN Hongxin.Time-frequency analysis of the direct sequence spread spectrum signals[J]. Journal of circuits and systems, 2004, 9(3): 23-28.
[8]TAO Luo, PASUPATHY S, SOUSA E S. Interference control and chip waveform design in multirate DS-CDMA communication systems[J]. IEEE transactions on wireless communications, 2002, 1(1): 56-66.
[9]ZHAO Chenglin, ZHANG Kun, SUN Xuebin, et al. Precoding with interference suppression sequence scheme for OFDM-based cognitive radio systems[J]. The journal of China universities of posts and telecommunications, 2011, 18(4): 59-64.
[10]SCHILLING D L, MILSTEIN L B, Pickholtz R L, et al. Optimization of the processing gain of and M-ary direct sequence spread spectrum communication system[J]. IEEE transactions on communications, 1980, 28(8): 1389-1398.
收稿日期:2015-04-27.
基金项目:国家自然科学基金项目 (61271263).
作者简介:郭黎利(1955-),男,教授,博士生导师; 李清伟(1987-),男,博士研究生. 通信作者:李清伟, E-mail: xinxishe@126.com.
doi:10.11990/jheu.201504063
中图分类号:TN911.6
文献标志码:A
文章编号:1006-7043(2016)04-0619-06
Effect of the spectrum overlap factor on digital modulation systems
GUO Lili, LI Qingwei, DAI Jia, LIU Xiangpu
(College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China)
Abstract:General performance analysis of a digital modulation system was performed mathematically in the time domain considering the statistical regularity of signal and noise. However, the performance of such a system cannot be accurately and quantitatively described for complex traffic environments by using the classical method. The difficulties encountered in doing so include the problems of avoiding narrow or wideband interferences and authorized users in the cognitive radio(CR) currently and in the future. To mitigate these problems, we propose the use of the spectrum overlap factor (SOF) for performance analysis of digital modulation systems in the frequency domain. Classical bit error rate (BER ) expressions of 2ASK, BPSK, and FSK modulation are derived and revised. A quantitative mathematical description is given by verifying the intuitive physical significance which means that the spectrum overlap worsens the system performance. The validity of the analysis in the frequency domain was confirmed by simulation.
Keywords:BER; time domain analysis; authorized users; spectrum overlap factor (SOF); digital modulation; frequency domain analysis
网络出版日期:2016-01-27.

