基于HyperStudy的航天器结构多目标优化设计
撰文/中国航天员科研训练中心 刘 磊 马爱军 刘洪英 石 蒙
基于HyperStudy的航天器结构多目标优化设计
撰文/中国航天员科研训练中心 刘磊 马爱军 刘洪英 石蒙
对于正在研制的载人航天某装置,设计过程中存在最小化质量、最大化一阶整体振动频率的多目标优化问题,文中基于HyperStudy平台,利用多目标遗传算法对其求解得到多目标的Pareto最优解集,并与加权目标法得到的优化解进行对比,最终确定了最优结构。优化后结构设计域质量降低11.7%,一阶整体振动频率提高2.7%,优化效果明显。
一、引言
航天器在发射过程中要经历复杂的动力学环境,因而在航天产品结构设计中振动是考虑的重要因素。而模态是结构振动形式的直接体现,在航天产品设计中,一般希望结构固有频率(特别是低阶频率)尽可能的大,以远离火箭发射过程中的振动频率,从而避免发生共振而造成结构损坏。另一方面,航天器发射过程中对装载的航天产品质量有着苛刻的要求,航天器质量每减少1kg,发射成本可以节省一万美元,因此航天产品结构的减重设计越来越得到重视。
对于正在研制的载人航天某装置,设计阶段对其进行有限元建模,然后进行模态分析,得到其固有频率和固有振型,在研制阶段对其进行优化设计,以达到节省研制周期与成本的目的。该装置有两个优化目标,一个目标是结构一阶整体振动频率最大,另一个目标是结构整体质量最小。
对于结构的多目标优化问题,可以采用加权目标法求解,为每一个目标设定一个权重系数,将多目标问题转化为单目标问题。加权目标法的一个明显缺点是权重系数人为给定,经验依赖性强,而且给定不同的加权系数会得到不同的优化解。为了得到结构质量与一阶整体振动频率的关系曲线,本文选择在结构有限元模型基础上,利用多目标遗传算法进行设计变量的优化迭代求解,可以得到两个优化目标的Pareto最优解集。同时利用加权目标法求解该多目标优化问题,并比较两种优化方法得到优化解的差异,最终确定最优结构。
本文中的优化设计基于HyperStudy多学科优化平台进行,HyperStudy可以直接引用HyperMesh中的有限元模型,并利用RADIOSS求解器进行求解,同时内置多种优化算法,方便设计者从中进行选择。
二、结构的有限元建模与模态分析
正在研制的载人航天某装置是由外部框架结构和内部诸多单机组成,外部框架结构为薄壁梁组成,有限元建模采用面网格进行建模,薄壁梁的尺寸可以进行一定幅度的调整。而内部单机为非重点考察对象,同时结构也不宜进行调整,为了提高优化设计求解迭代效率,在单机质心处利用质量点单元模拟单机产品,并通过刚性单元与单机的框架安装点进行连接。框架之间通过螺栓或焊接进行连接,模型边界条件为结构通过底板一系列安装孔进行完全约束,最终结构有限元模型如图1所示。
对结构进行模态分析,得到结构的一阶整体振动频率为48.7Hz,一阶整体振动振型如图2所示。

图1 载人航天某装置有限元模型
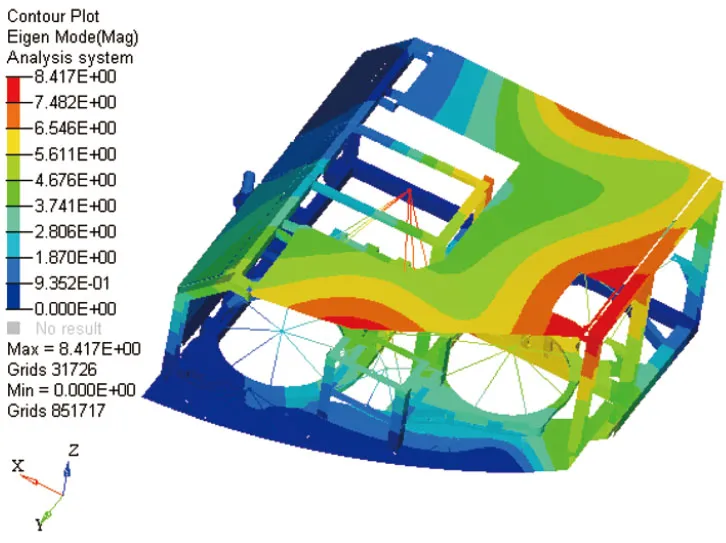
图2 载人航天某装置一阶整体振动振型
三、基于多目标遗传算法的结构多目标优化
1.优化问题描述
结构的内部单机及框架整体拓扑构造都不能进行调整,因而优化设计变量选定为结构的外部框架部分薄壁梁尺寸,优化设计变量共10个。优化的目标有两个分别为一阶整体振动频率最大(用Freq表示),结构设计域质量最小(用Mass表示)。此时优化问题的数学模型可以表示为式(1),结构的尺寸设计变量初始值、上下限如表1所示。


表1 设计变量初始值、上下限
2.多目标遗传算法优化的Pareto最优解集
此多目标优化问题基于HyperStudy平台进行,在有限元模型基础上利用多目标遗传算法进行求解,设置最大迭代次数为100,其余参数取默认值,图3为多目标优化的Pareto最优解集。
四、基于加权目标法的结构多目标优化
1.加权目标法的优化数学模型
加权目标法的基本思想是:通过了解结构设计需求,来确定各个优化目标的权重,将每个设计目标函数乘以相应的加权系数并求和后,就可以将多目标优化设计问题转化为单目标优化设计的目标函数。
对于质量、频率两种不同的目标,可通过将其与初值之比作为目标来实现单位的规划统一,同时用最小化频率的倒数作为优化目标来代替最大化频率。此时,加权目标法的优化数学模型可以表示为式(2)。
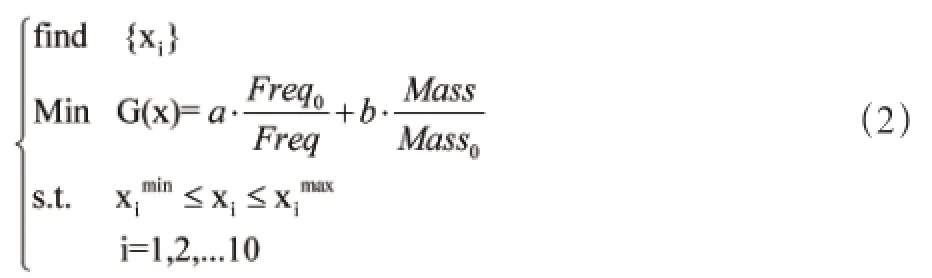
其中Freq0为结构初始一阶整体振动频率,Mass0为结构初始质量。而a和b分别是权重系数,其中a+b=1。
2.加权目标法的优化解
加权目标法同样基于HyperStudy平台进行,在有限元模型基础上对于加权后的目标函数选择利用序列二次规划法(SQP)进行优化迭代求解。
(a) 取权重系数为a=b=0.5,此时加权目标为G1(x)。经过15次迭代,结果收敛。此时优化后结构一阶整体振动频率为40.7Hz,设计域质量为3.52kg。
(b)取权重系数a=0.75, b=0.25,此时加权目标为G2(x)。经过25次迭代,结果收敛。此时优化后结构一阶整体振动频率为53.7Hz,设计域质量为6.52kg。
(c) 取权重系数a=0.75, b=0.25,此时加权目标为G3(x)。经过10次迭代,结果收敛。此时优化后结构一阶整体振动频率为41.1Hz,设计域质量为3.60kg。
加权目标G1(x),G2(x),G3(x)的迭代曲线分别如图4(a)、4(b)、4(c)所示。

图4 目标函数G(x)迭代曲线
五、分析与讨论
为了更直观观察结构优化前后的两个目标变化情况,将其表示成坐标形式(Freq, Mass)。结构优化前一阶整体振动频率为48.7Hz,优化前设计域质量为6.00kg,则其坐标为A(48.7, 6.00)。由加权目标法得到的三个优化解坐标分别表示为G1(40.7, 3.52),G2(53.7, 6.52),G3(41.1,3.60)。将各个坐标分别在多目标优化的Pareto最优解集中表示,以便于最优结构的确定,如图5所示。
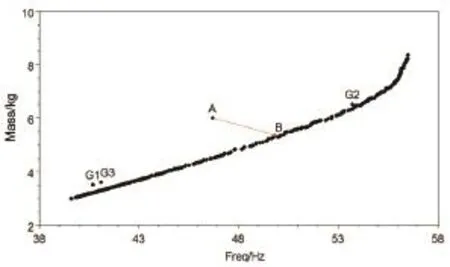
图5 最优结构的确定示意图
案例表明利用加权目标法求解时,赋予不同的权重因子,会得到不同的优化解。从图5中还可以看出,G1、G2、G3三个坐标点均在Pareto最优解集的左上方,表明利用多目标遗传算法求解得到的Pareto最优解集相比于加权目标法得到的优化解更优。其中G1、G3点相比于优化前的结构在质量降低的同时,一阶整体振动频率也大幅度的降低;而G2点恰恰相反,虽然一阶整体振动频率有了一定幅度的提高,但质量却有所增加,因此都不是满意方案。
综上所述,最优解需在Pareto最优解集中进行选择,最终选定为图5的B点,此时结构一阶整体振动频率为50Hz, 相比于优化前的48.7Hz提升2.7%;设计域质量为5.30kg,相比于优化前的6.00kg降低11.7%,优化效果较好。B点对应的优化后结构尺寸如表2所示。

表2 设计变量优化解
六、结语
本文基于HyperStudy平台,对正在研制的载人航天某装置进行多目标优化设计,利用多目标遗传算法求解得到设计域质量和一阶整体振动频率的Pareto最优解集,并与加权目标法得到的最优解进行对比,结果表明多目标遗传算法在求解结构多目标优化问题上具有一定的优势。最终确定了最优结构,与最初结构相比,两个优化目标均有了明显的改善,取得了很好的优化效果,节省了产品的研制周期与成本,可以为类似航天产品的优化设计提供一定的参考。

