自然界中的数学谜题
雪花 雪花的对称,令人惊叹大自然的神奇。雪花显示出6方径向对称,每片“花瓣”的精致图案完全相同。目前科学家尚未彻底破解动植物的对称之谜,而非生命物质的对称更让他们抓耳挠腮。雪花的形成,是源于水分子固化时的天然排列。这个过程很复杂,但基本上是这样的:水分子结晶时,它们彼此之间形成弱氢键。这些键的排列是为了让吸引力最大化,让排斥力最小化。这就是雪花呈清晰六边形的原因。没有哪两片雪花是一样的。为什么片片雪花自身完美对称,而每片雪花却都不一样?当每片雪花从天空飘落时,它都会经历独特的大气条件,比如风和湿度,而这些因素会影响生成雪花的冰晶。雪花的每个瓣片都受同样的因素影响,因此结晶方式一样,每个瓣片都是其他瓣片的精确镜像。

平行沙丘 在数学中,两条平行线延伸无限远,既不汇合也不相交。图中,澳大利亚沙漠中的平行沙丘并不像平行线那么完美。虽然物理世界中的完美很少见,但那些近似或比较近似的自然的“完美”,依然令我们惊艳。

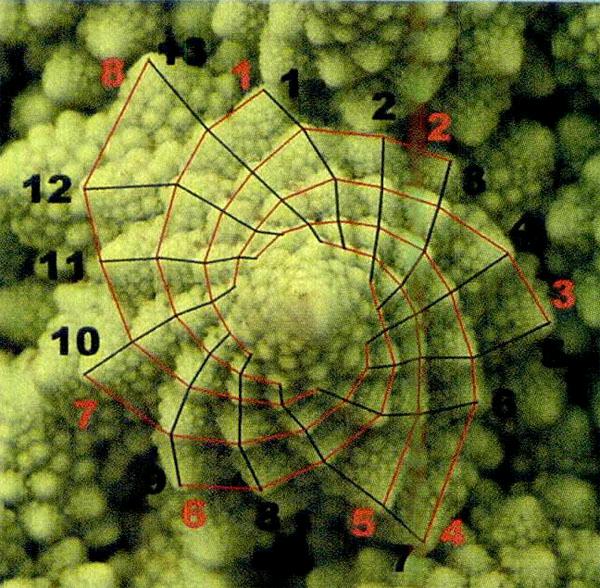
宝塔花菜 宝塔花菜的形状不同寻常,许多人以为它是一种转基因花菜,但它实际上是自然界许多分形几何案例的代表之一。在几何学中,分形几何体是指一类复合几何体,其中每个构件与整体的模式相同。对宝塔花菜来说,每个菜茎都是整棵花菜的对数螺旋形状的微型版。这意味着,整棵宝塔花菜是一个大的对数螺旋形,由较小但形态完全相同的锥形迷你螺旋组成。当然,和别的花菜一样,宝塔花菜也富含维生素,同时造型独特,这可能就是孩子们喜欢吃宝塔花菜的原因。
葵花 葵花拥有径向对称和一种数字对称——斐波那契数列。在斐波那契数列中,每个数字都是前面两个数字之和,例如:1,2,3,5,8,13,21,34,55……以此类推。科学研究发现,葵花种子(瓜子)从葵花中心向外延伸的螺旋数量,构成了斐波那契数列。这并非罕见,许多植物都以斐波那契数列方式产生叶片、花瓣和种子。之所以很难找到四叶苜蓿——幸运草,就是这个道理。那么,植物为什么要遵循数学规则?科学家推测,这是为了提高效率。简单地说,如果每颗种子都以一个无理数角度被隔开,葵花就能最大数量地塞满种子。“最无理”的无理数被称为黄金分割或黄金比例。巧的是,用斐波那契数列中每个数除以它后面那个数,其所得值都很接近黄金分割值0.618。因此,对于遵循斐波那契数列的任何植物来说,其每颗种子、每片叶子、每朵花或每根枝条之间,都有一个符合黄金分割的角度。
蜂巢 几百年来,人类一直惊叹于蜂巢中的六边形。这可是蜜蜂本能创制的形状。人类要想制作完美的六边形,需要借助圆规和尺子。蜂巢是壁纸对称的范例之一。所谓壁纸对称,是指把正六边形图案不断重复,直到盖满一个平面。这方面的其他案例包括马赛克画和铺满瓷砖的地面。数学家相信,蜜蜂采用六边形建造蜂巢,是因为对于采用最少的蜂蜡来储存最多的蜂蜜来说,累积正六边形最有效。而像圆圈之类的形状,相互紧挨着排列时避免不了空隙,效率自然不够。但有些学者认为,蜂巢的正六边形只是个意外,而不是蜜蜂自己想出来的。他们猜测,当圆形巢室周围的蜂蜡坍塌时,就会形成正六边形。不管上面两种理论中的哪种是正确的,蜂巢都无疑是自然界中令人着迷的一个对称范例。

圆蛛网蜘蛛 现已知大约有5000种圆蛛网蜘蛛。它们全都编织接近完美的圆形蛛网,蛛网中央伸出接近等距离的径向支撑,于是一组同心圆大网被编织出来捕捉猎物。圆蛛网蜘蛛为什么这么喜欢几何学?目前仍不清楚。测试表明,在抓捕猎物方面,圆蛛网并不比不规则形状的蛛网更有效。一些科学家推测,当蜘蛛的天敌与圆蛛网接触时,圆蛛网的径向对称有助于平衡分散撞击力量,蛛丝被撞断的情况会少些。然而,若真是这样的话,为什么其他蜘蛛不编织对称的蛛网呢?有些蜘蛛有能力编织圆蛛网,但看来它们却不费心这么干。如此看来,圆蛛网之谜还待揭晓。

孔雀 大多数动物具有双侧对称,即有一条中分线把身体分隔成相同的两半。孔雀把这种对称发挥到了极致。事实上,大生物学家达尔文很讨厌孔雀。他在1860年的一封信中写道:“一看见孔雀尾巴羽毛,我就会恶心!”他认为孔雀尾没有进化意义,完全是个负担。他的这种愤怒一直持续到他提出性选择理论时才结束。该理论认为,动物为了增加交配机会而演化出某些特征。这些特征包括明亮的颜色、更大的个头、对称的体形和羽毛上重复的图案等。

人脸 人类具有双侧对称。研究表明,一个人的对称性对于这个人的吸引力来说非常重要。人类的脸和动物的一样,充满黄金分割的例子。例如,人的嘴巴和鼻子分别位于眼睛和下巴之间的黄金分割位置。甚至,人的眼睛和耳朵自身也呈现螺旋。虽然每个人都不一样,但整个人体的许多平均数都靠近黄金分割,而且越靠近越有吸引力。例如,在最漂亮的笑容当中,中门齿比侧切齿宽0.618倍,侧切齿比犬齿宽0.618倍,以此类推。从演化心理学角度讲,我们之所以都具有遵循黄金分割的生理特征,有可能是因为黄金分割是生育力强的一个潜在指针。

细菌 诸如希瓦氏菌的一些细菌,通过在短短40分钟里让自己数量翻倍的方式进行繁殖。在这样的数列中,每个数字都是前面那个数字的2倍。就这样,在很短时间内,细菌数量猛升。
银河系 在地球上,对称及其他数学模式无处不在。但这些自然法则是地球独有的吗?银河系边缘的一个新部分最近被发现。通过对此进行研究,天文学家现在相信银河系是近乎完美对称的。运用这一新信息,他们对自己的理论更自信:银河系只有两条主臂,即盾牌座和英仙座,这两条臂互呈镜像。除了镜对称之外,银河系还有另一个惊人的设计:就像鹦鹉螺的壳和葵花籽的排列一样,银河系的每条臂都象征着始于银河系中心(银心)、向外延伸的一个对数螺旋。

火山锥 火山形成锥体,其陡度和高度取决于熔岩黏度。流动快、水分多的熔岩形成的锥比较扁,黏度大的熔岩形成的锥比较陡。锥体是三维立体,其体积容易计算,火山锥也一样。

