蚌埠市PM2.5影响因素及分布演变规律计量分析
潘婷婷,朱家明,滕 磊,洪 玲
(1.安徽财经大学金融学院,安徽蚌埠233030;2.安徽财经大学统计与应用数学学院,安徽蚌埠233030)
蚌埠市PM2.5影响因素及分布演变规律计量分析
潘婷婷1,朱家明2,滕 磊2,洪 玲2
(1.安徽财经大学金融学院,安徽蚌埠233030;2.安徽财经大学统计与应用数学学院,安徽蚌埠233030)
针对蚌埠市空气中PM2.5的影响因素及分布演变规律,综合使用统计分析、定量分析、相关分析、趋势分析等方法,分别构建多元线性回归、时空分布、高斯烟羽扩散等模型,使用SPSS、EVIEWS、EXCEL等软件编程求解,研究得到PM2.5与NO2、O浓度大小成负相关、与PM10、CO、NO2浓度成正相关,PM2.5的扩散范围越广浓度越小、湿度越大PM2.5的扩散范围越小、PM2.5与温度相关性不大等结论。
PM2.5;回归分析;高斯烟羽模型;EVIEWS;SPSS
自2013年初以来,中国发生大范围持续雾霾天气,据发改委披露,受影响的雾霾区域约占国土面积的1/4,受影响人口多达约6亿人。环境保护部于2012年2月颁布了新修订的《环境空气质量标准》(GB3095—2012),规定中将空气质量指数AQI作为空气质量监测指标,首次将产生灰霾的主要因素PM2.5的浓度指标列入基本监测指标。
目前国内集中研究气体SO2、NO2和O3等的垂直分布特征,而对近地层PM2.5的垂直分布特征研究甚少。Wu(2002)等[1]对澳门城区的道路两旁2~79m内PM2.5浓度的11h监测结果表明,PM2.5浓度随高度增加呈递减趋势。杨龙(2005)[2]选取秋冬两季各14d,对北京地区距地面高8~320m范围内ρ(PM2.5)的垂直分布进行监测,获得近地层垂直廓线;并结合同步测得的风速、风向、温度以及湿度等气象数据,对其垂直分布的影响进行分析,最终拟合了ρ(PM2.5)的垂直廓线方程。国外研究以探索人为破坏源头的数据为出发点,较少分析影响PM2.5内部各个理化因素的影响。马小铎(2015)[3]使用近几年采集到的数据,通过对这些数据的研究,给出了PM2.5现象的时间规律、其与地理的相关关系、PM2.5的自然成因和人为成因,借助统计分析及数学建模的方法,找到PM2.5污染物的各种理化影响因素之间的相关关系和扩散与消退的一般规律,进而从数学上进行量化分析。
本文针对蚌埠市大气环境质量状况偏差,雾霾现象时有发生的现状,从蚌埠市PM2.5的成因、PM2.5污染物的各种理化影响因素及分布演变规律等相关方面进行计量研究,对于缓解和改善城市空气质量问题具有重要意义。
1 数据来源与模型假设
蚌埠市2015年1月到7月每天的PM2.5、PM10、CO、SO2、O3指标含量及AQI指数、质量等级、当天AQI排名以及蚌埠市不同监测点及全市平均PM2.5数据均来自青悦空气质量数据库[4]、天气预报及中国空气质量在线监测分析平台[5]。为了便于解决问题,提出以下假设:(1)蚌埠市的地理特性比较均匀,故忽略地理因素对气象的影响,各监测点PM2.5的数据分布是相互独立的;(2)不考虑蚌埠市以外的其他因素对该地区的气象影响;(3)风速均匀,风向不变;(4)在水平和垂直方向上PM2.5的扩散过程都服从正态分布;(5)PM2.5扩散空间的风速及大气稳定度都是均匀、稳定的;(6)污染物在风向上呈线性分布,在其他方向上按高斯分布;(7)源强连续均匀;(8)物质均满足守恒定律。
2 PM2.5及其影响因素相关性及独立性分析
2.1 研究思路
首先对收集到的数据利用EXCEL软件进行整理,并做出各变量的趋势图分析得出各变量具有大致相同的分布趋势,再进行相关性和显著性分析,得到AQI中6个基本监测指标的相关关系,并进一步对PM2.5含量与其它5项指标及其对应污染物含量之间的相关性进行分析,借助EVIEWS软件先进行多元线性回归得到相应模型,通过模型的R2值判断其拟合优度,并利用F值、t值进行显著性检验,对模型不断进行优化,最终得到PM2.5含量与其它5项指标含量的多元回归关系式。
2.2 数据处理
为了让数据分析的结果更为直观,先利用EXCEL对AQI中6个基本监测指标PM2.5、PM10、CO、NO2、SO2、O3含量作出其随时间变化的趋势图,如图1所示。

图1 PM2.5、PM10、CO、NO2、SO2、O3含量变化趋势图
根据无量纲化后蚌埠市2015年1月到7月每天对应的PM2.5、PM10、CO、NO2、SO2、O3浓度数据,利用SPSS软件进行各变量间相关系数分析,得到PM2.5、PM10、CO、NO2、SO2、O3各变量间的相关系数,如表1所示。

表1 PM2.5及各变量间偏相关性分析
由表1可得各个指标间的相关系数和显著性值。从表1中可知PM2.5与PM10、CO、NO2、SO2、O3显著性sig值低于0.01,且相关系数分别为0.875、0.656、0.425、0.324和0.041,说明PM2.5与其均有着较强的正相关关系,而PM2.5与O3的显著性sig值为0.558,远大于0.01,说明其线性相关性不显著。同理可知O3与PM2.5、NO2、CO、SO2的显著性sig值大于0.01,表示在0.01的显著性水平上肯定了它们之间不相关的假设,即它们之间不存在显著相关关系,但O3与PM10之间双侧显著性sig值都小于0.01,且相关系数为0.230,说明存在较显著的正相关性。综合分析可得,PM2.5、PM10、CO、NO2、SO2两两之间除了CO与SO2之间的双侧显著性sig值大于0.01,无较强相关性外,其余的两两之间在0.01水平下都存在着较显著的正相关关系。
2.3 结果分析
对PM2.5含量与PM10、CO、NO2、SO2、O3含量之间的相关性利用EVIEWS软件进行多元回归分析,这些指标分别用x1,x2,x3,x4,x5,x6表示。由回归结果分析可知,虽然方程总体的R2=0.850854>0.8,模型的拟合优度较高,且F=233.8975模型整体的显著性较高,PM10、CO、NO2、SO2的t检验值均通过检验,但由于O3的t=-1.754611<2,所以该值通不过检验,故考虑对O3进行对数变换,再次进行多元回归分析,得到结果如表2所示。
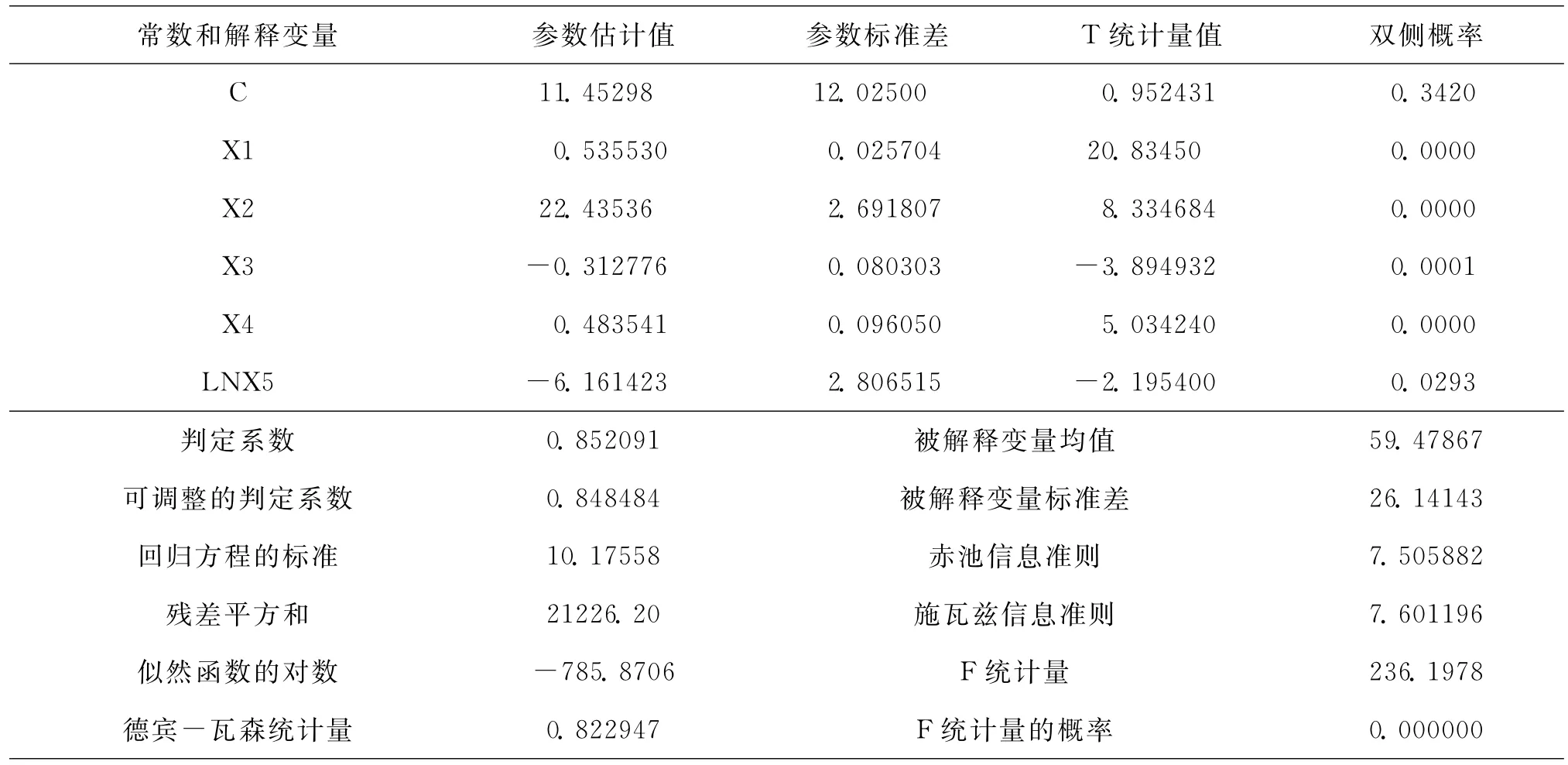
表2 对数变换后进行多元回归分析结果
由表2分析可得,方程总体的R2=0.852091>0.8,模型的拟合优度较高,且F=236.1978模型整体的显著性较上一次回归结果有所提高,PM10、CO、NO2、SO2、O3的t绝对值均大于2,各指标显著性水平较高,由方程的DW=0.822947可知,该模型不存在自相关性,通过检验,由此可得多元回归方程为:

由此表达式可知,PM2.5的浓度变化除了与SO2呈对数相关,与其余空气污染物浓度变化均呈线性相关,且PM2.5的浓度变化与PM10、CO、SO2的浓度呈正相关性,而与NO2、O3的浓度呈负相关性。
3 PM2.5时空分布规律及污染评估
3.1 研究思路
根据蚌埠市不同监测点(百货大楼、蚌埠学院、二水厂、高新区、工人疗养院、淮上区政府)及全市平均PM2.5数据,初步分析不同监测点与全市平均PM2.5指数随时间变化趋势大体相同,故选取全市平均PM2.5指数为例,描述各监测点的时间分布。对于空间分布,为描述不同监测点的PM2.5指数分布,根据PM2.5检测空气质量新标准[6]对PM2.5指数进行了等级划分,然后用EXCEL的数据透视功能,统计6个监测点中PM2.5指数各等级出现的频率,进行不同区域的污染评估。
3.2 数据处理
根据青悦空气质量历史数据库[4],整理蚌埠市2015年1月到7月的百货大楼、蚌埠学院、二水厂、高新区、工人疗养院、淮上区政府6个监测点及全市平均的每日各时点PM2.5指数。用EXCEL软件做出蚌埠市6个监测点及全市平均的每日各时点PM2.5指数变化趋势图,如图2所示。

图2 各监测点及全市平均PM2.5指数趋势图
各监测点及全市平均PM2.5指数随时间变化趋势大致相同,都随着时间的增加呈减少趋势,故可用全市平均PM2.5指数随时间变化规律描述6个监测点PM2.5指数的时间分布。由图2分析可知,蚌埠市2015年1月至7月的PM2.5指数在0~250μm/m3内变化。PM2.5指数在1、2月的值高于其它月份,从2015年1月2日凌晨0点开始,污染物逐渐累积,到1月5日22:00第一次到达高值254μm/m3,1月6日到1月23日PM2.5指数增减幅度较小,总体呈下降趋势,空气中污染物有所减少。1月24日开始,颗粒物质量浓度逐渐增大,且在2月PM2.5指数值总体较大。3月开始,污染物较前一段时间开始减少,PM2.5指数呈下降趋势,但仍有几个指数值高的污染点。
3.3 结果分析
用EXCEL筛选出百货大楼、蚌埠学院、二水厂、高新区、工人疗养院、淮上区政府6个监测点的PM2.5指数值,利用数据透视表功能统计各监测点的不同PM2.5指数值的频数,然后根据PM2.5指数等级划分标准,统计各监测点不同PM2.5指数等级出现的频率,得到结果如表3所示。

表3 各监测点PM2.5指数频率统计表
表3直观地表现了6个监测点的污染情况,二水厂污染较其它监测点而言最为严重,PM2.5浓度超过100μm/m3的概率高达14.68%,工人疗养院、百货大楼、淮上区政府的PM2.5指数超过100μm/m3的概率均在10%以上,分别为14.23%、13.14%、11.12%,蚌埠学院、高新区环境质量较好,PM2.5浓度为Ⅱ级以下的概率高达92.03%与91.72%。
由表3可知工人疗养院、蚌埠学院、淮上区政府、高新区的PM2.5指数频率的最大值均在0~50μm/m3这一范围内,百货大楼、二水厂的最大频率在50~100μm/m3范围内,对照PM2.5指数等级划分标准可知,工人疗养院、蚌埠学院、淮上区政府、高新区这4个监测点的空气质量为优,受污染程度很低,而百货大楼、二水厂两个监测点的空气质量为良,污染较小。
4 PM2.5扩散与衰减的演变规律
4.1 研究思路
为研究蚌埠市PM2.5的发生和演变规律,整理据中国空气质量在线监测分析平台[5]搜集到蚌埠地区温度、湿度、风力等数据,这些指标分别用x6,x7,x8表示,建立高斯烟羽模型研究蚌埠地区PM2.5的扩散和衰减等规律,并运用EVIEWS软件将8个变量综合考虑,不断拟合得到最终多元回归方程,综合分析各因素间的定性和定量关系,并通过取具体时间点的污染物含量带入模型计算,检验高斯烟羽扩散模型的可靠性。
4.2 研究方法
①建立高斯烟羽扩散模型[7],设C (x,y,z,h)是距离污染源位置的空间距离为h的点(x,y,z,h)处PM2.5的浓度。任取一个闭曲面S,它所围的区域是V,由于扩散的存在,从h到h+Δh这段距离内,通过S流入V的质量,由高斯公式得:

在扩散过程中由于土壤吸收、风速作用及地表径流等造成PM2.5在传播过程中有所流失,造成PM2.5的浓度有一定的衰减,由于物质守恒定律,PM2.5在V内由于扩散与衰减的联合作用,导致实际上存在于V内的浓度为:
则PM2.5污染物的浓度计算公式为:

其中Δh,h,V是任意取值的。
题中要求计算高架点源的地面浓度公式,则令z=0,并进一步令y=0,得到沿X轴线上的浓度分布公式:

式中:C′—空间点(x,y,z)的污染物浓度,mg·m-3;
C—源强,单位时间污染物排放量,mg·m-3;
V—平均风速m·s-1;
σy,σz—污染物扩散系数,与水平距离X和大气稳定度有关,并随X的增大而增加。
其中,a2,b2,c2分别是沿(x,y,z)方向的扩散系数,扩散系数是表示扩散范围及速率大小的特征向量。
②多元线性回归预测PM2.5发生与演变规律[8]。由于实际情况中影响y大小的因素很多,多个变量之间与y之间存在着如下的线性关系:

其中:α0,α1,α2…αk是回归系数,X0,X1,X2,…Xk是可测量的自变量,ε为随机误差项,满足
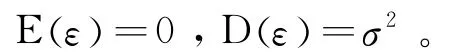
根据模型①②计算出矩阵Lij和矩阵Liy:
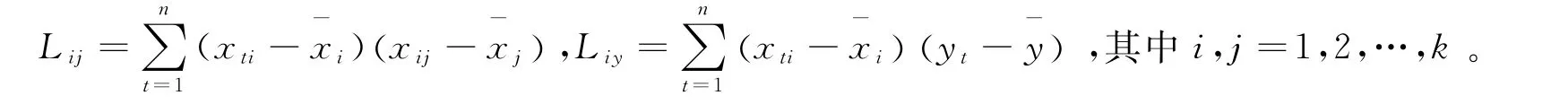
最后,根据公式求出回归系数的估计值:

即可求出回归模型的表达式为:

本题考虑到空气中五项污染物指数以及三个气象条件共8个因素,故得到如下模型:

4.3 数据处理
综合高斯烟羽扩散模型和多元线性回归模型,定量与定性相结合,合理考虑风力、湿度、温度等因素,探索PM2.5的成因、演变(扩散与衰减)等一般性规律。
首先借助EVIEWS软件利用上述所给回归模型,将8个因素进行多元线性回归,并不断拟合得到结果如表4所示。
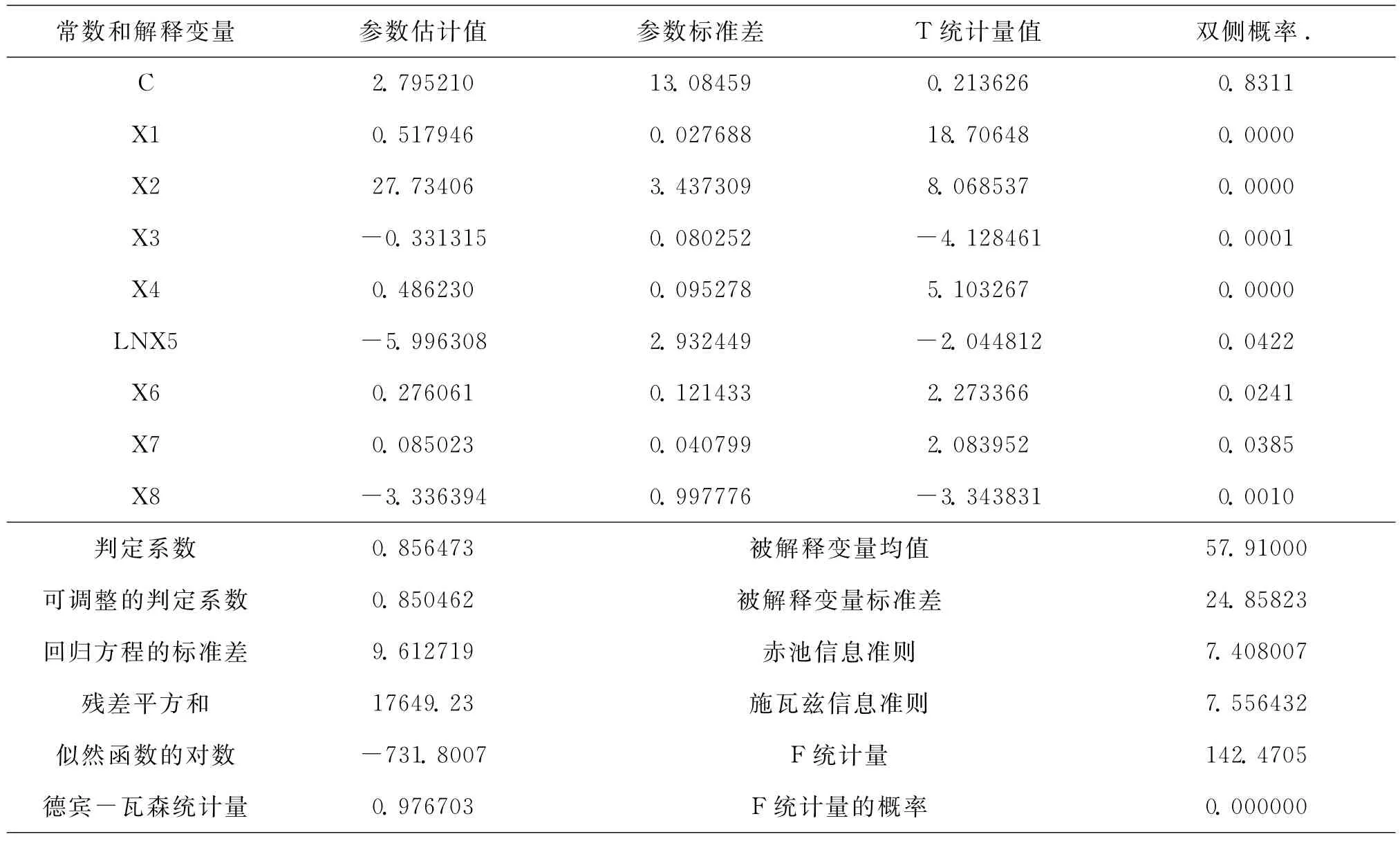
表4 多因素回归分析后结果
由表4可知,R2=0.856473模型拟合优度较高,F=142.4705模型显著性水平较高,各因素t值均通过检验,各因素的显著性水平较高,由DW=0.976703,该模型不存在自相关性,故多元回归模型为:

根据表达式分析可知,PM2.5的浓度变化除了与SO2呈对数相关,与其余空气污染物浓度及气象条件变化均呈线性相关,且PM2.5的浓度变化与PM10、CO、SO2的浓度及风力、湿度变化呈正相关性,而与NO2、O3的浓度及温度变化呈负相关性。
4.4 结果分析
由各变量对PM2.5浓度的相关系数可知:NO2、O3、风力与PM2.5浓度成负相关,NO2、O3浓度越大,PM2.5浓度反而越小;风速越大,PM2.5浓度也越小,因为PM2.5在扩散过程中存在衰减。由于高压反气旋天气有利于污染物的扩散,这也使得PM2.5存在于很多地区。

图3 各变量及PM2.5的含量变化趋势图
由分析综合可知,PM2.5的产生与PM10、CO、NO2、SO2、O3含量都成正线性相关关系,其中O3与PM2.5含量成对数相关,与其余各因素的线性相关性均较强,PM2.5含量随PM10、CO、NO2、SO2、O3含量的增大呈明显增大趋势。PM2.5形成原因复杂,来源广泛,但主要是人为排放所致。人为排放部分包括生物质和石化燃料等的燃烧、工业粉尘、建筑施工和道路扬尘、餐饮油烟等污染源直接排放的颗粒物,也包括由一次性气态排出物的二次转化颗粒物。PM2.5的扩散[9]很大程度上取决于风力、湿度因素,风力越大,PM2.5的扩散范围越广;而浓度越小、湿度越大,PM2.5的扩散范围越小,但由分析结果可知,PM2.5含量与温度相关性不大。
为了验证PM2.5演变预测的多元线性回归模型的准确性[10],通过将具体值带入前面所建立的高斯烟羽扩散模型,并检验相应的可信度和可靠性水平。将监测点区域的PM2.5扩散分布情况与当天各观测点实际检测指数值做比较可以看出,各地区PM2.5浓度计算值基本和最后观测到的实际PM2.5实际质量指数值走势相一致,有些差异较大的监测点表明该处当天所产生PM2.5量较多,导致计算出的扩散值小于实际观测值;差异较小点表明该处产生PM2.5较少,基本为其它地方扩散而来。这也表明我们所做的PM2.5污染扩散模型拟合效果较佳,基本能够描述出PM2.5污染物扩散和衰减情况。
5 结论
针对PM2.5成因间相关性及独立性分析、PM2.5时空分布规律及污染评估以及PM2.5扩散与衰减的演变规律等问题,采用趋势分析、统计分析、相关性分析等多种分析处理方法,建立多元线性回归、时空分布、高斯烟羽扩散模型等模型进行研究,综合运用多种软件对问题进行简洁科学的处理,从而使问题得以更全面的分析,较好地解决了蚌埠市PM2.5的影响因素及分布演变规律问题。研究可知,PM2.5的浓度与其他空气污染物浓度及气象条件均有一定的联系,文中采用的预测模型较全面的考虑了这些因素的综合影响,其预测结果能很好地帮助人们制订出行计划,具有一定的指导价值。
[1]Wu Ye,Hao Jiming,Fu Lixin,et al.Vertical and horizontal profiles of airborne particulate matter near major roads in Macao,China[J].Atmos Environ,2002,36:4907-4918.
[2]杨龙,贺克斌,张强,等.北京秋冬季近地层PM2.5质量浓度垂直分布研究[J].环境科学研究,2005,18:24-28.
[3]马小铎.影响PM2.5的理化因素及相关问题的模型研究[D].北京:北京交通大学,2015:15-28.
[4]上海青悦信息.青悦空气质量历史数据库[EB/OL].[2015-08-01].http://air.epmap.org/.
[5]中国空气质量在线监测分析平台[EB/OL].[2015-08-02].http://www.aqistudy.cn/.
[6]PM2.5监测空气质量新标准[EB/OL].[2015-08-02].http://www.360doc.com/content/14/0304/17/276037_357701073.shtml.
[7]董赫,翟哲,李夺.高斯烟雨扩散模型在空气中PM2.5实际问题的应用[J].黑龙江八一农垦大学学报,2014,26(3):69-73.
[8]蒋雪峰,李洁,蒋奎.空气中PM2.5问题的建模研究[J].数学的实践与认识,2014,44(15):47—58.
[9]污染物的稀释法控制[EB/OL].[2015-08-02].http://www.docin.com/p-198930945.html?qq-pf-to=pcqq.c2c.
[10]覃太贵,尹辉,雷林.PM2.5相关因素及分布演变的研究[J].数学的实践与认识,2014,32(8):31-37.
Quantitative analysis of Bengbu PM2.5 affecting factors and distribution evolution
PAN Ting-ting1,ZHU Jia-ming2,TENG Lei2,HONG Ling2
(1.School of Finance,Anhui University of Finance and Economics,Bengbu Anhui 233030,China;2.School of Statistics and Appl.Math,Anhui University of Finance and Economics,Bengbu Anhui 233030,China)
For Bengbu air Factors evolution and distribution of PM2.5,Integrated use of statistical analysis,quantitative analysis,correlation analysis,trend analysis and other methods,respectively constructed multiple linear regression,spatial and temporal distribution,Gaussian plume diffusion model,use SPSS,EVIEWS,EXCEL software programming to solve,study was PM2.5and NO2、O3concentration was negatively correlated with the size,PM2.5andPM10、CO、NO2concentrations were positively correlated size,the more wide diffusion range PM2.5concentrations less,the greater moisture,the smaller diffusion range of PM2.5,PM2.5had little correlation with temperature and other conclusions.
PM2.5;regression analysis;Gaussian plume model;EVIEWS;SPSS
X513
A
1004-2237(2016)03-0017-08
10.3969/j.issn.1004-2237.2016.03.005
2015-12-01
国家自然科学项目(11301001);安徽财经大学教研项目(acjyzd201429)
潘婷婷(1994-),女,安徽芜湖人,安徽财经大学金融学院在校学生,主要从事金融与经济计量分析。
朱家明(1973-),男,安徽泗县人,副教授,硕士,主要从事应用数学与数学建模研究。E-mail:zhujm1973@163.com

