求first集的改进算法
熊鹏荣
(上饶师范学院数学与计算机科学学院,江西上饶334001)
求first集的改进算法
熊鹏荣
(上饶师范学院数学与计算机科学学院,江西上饶334001)
对
[1]和[2],给出的求文法G的终极符和非终极符的首符集算法进行改进,改进的算法使原算法循环需要进行(n1+n2)m次,减少为循环只需要进行n1+n2*m次。
文法;首符集;算法
编译程序是将高级语言程序翻译成机器语言的系统软件,对编译程序设计的基础理论研究很有必要。求文法G的终极符和非终极符的首符集是编译程序中自顶向下语法分析方法过程中的一个算法。求文法G的符号V的首符集的方法有根据定义求first集法和由关系图求文法符号的first集[1-3]。本文对参考文献[1]和[2]中对文法G的符号V的求first集算法做出优化改进,使得算法的效率更高。
1 文法的基础知识
定义1 设G=(VT,VN,S,P)是一个四元组,
其中VT是有限的终极符集;
VN是有限的非终极符集;
S是初始符,S∈VN;
P是产生式的有限集且形式:A→X1X2…Xn,其中A∈VN,Xi∈(VT∪VN)*(i=1,2,…,n),称四元组G为上下文无关文法,记VT∪VN=V,称V为文法G的字母表,且VT∩VN=φ。
对于一个可用的文法应满足的条件是其一,∀A∈VN都至少出现于一个产生式的左部,且∀a∈VT至少出现于一个产生式的右部中;其二,∀A∈VN都能推导出VT中的元素终极符。
定义2 设G=(VT,VN,S,P)是上下文无关文法,first(β)={a|β⇒*aγ,a∈VT,β,γ∈V*}∪(ifβ⇒*εthen{ε}elseφ),称集合first(β)为β首符集。
由定义可得,若X∈VT,则first(X)={X},对于空串ε有first(ε)={ε}。
2 算法的改进
[1]和[2]中给出了对每个X∈VT∪VN,求首符集的算法。在该算法的第3步为:Changes=F;
对P中的每个产生式A→X1…Xi…Xn,do{
Oldfirst=first(A);

若Oldfirst≠first(A),则Changes=T}
其中A→X1…Xi…Xn(表示Xi是产生式右部中第一个不可推导ε的符号)。
但该步骤是可以改进优化的,使该算法的效率更高。
将产生式集P分为两个子集:
第一个子集是P1={A→aβ|A∈VN,a∈VT,β∈V*};
第二个子集是P2=P-P1。
由此可得P=P1∪P2。
原算法中第3步中,对P1中的产生式形式为A→aβ,有
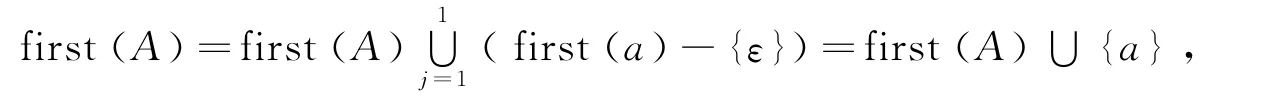
该式子说明只要first(A)含有终极符a,无论该产生式以后使用多少次计算①式操作,再也不能为first(A)增加一个终极符元素。这样可以将P1中产生式在循环中计算①式操作,移到循环外计算①式操作,而不会改变求first(A)集的结果。故可以将算法进行改进,使算法的效率更高。
对每一个X∈V,求first(X)的改进优化算法如下:
(1)当X∈VT,有first(X)={X};
(2)当X∈VN,有若X⇒*ε,则first(X)={ε},否则first(X)=φ;
(3)对P1中的每个产生式A→aβ|A→a,有first(A)=first(A)∪{a};
(4)Changes=F;
对P2中的每个产生式A→X1…Xi…Xn,do{
Oldfirst=first(A);
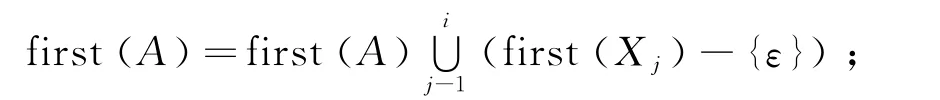
若Oldfirst≠first(A),则Changes=T}
(5)若Changes=T,则转(4);
(6)算法结束。
该改进算法由于将产生式P的子集P1移到循环外计算①式操作,这样在循环中可以减少循环中的运算量。
设|P1|=n1,|P2|=n2,步骤4的循环次数为m,则原算法中,在循环中对每个产生式都需要进行计算①式的操作,共需要进行(n1+n2)*m次计算①式的操作,改进后的算法,由于将产生式P的子集P1移到循环外,在循环中只是需要对P2中产生式的进行计算①式的操作,再加上P1中产生式在循环外进行一次计算(1)式的操作,故改进算法只需要进行n1+n2*m次计算①式的操作,比原算法减少了n1(m-1)计算①式的操作。这样减少算法的工作量,从而提高算法的效率。
高级语言PASCAL用上下文无关文法G[4]定义的过程中,文法G的产生式集P共有318条产生式,其中产生式集P1的产生式为152条,占总数47.78%,故该算法的改进在实际上是可以提高算法的效率,有一定的实际应用价值。
参考文献:
[1]金成植.编译程序设计原理[M].北京:高等教育出版社,2000:70.
[2]吕映芝.编译原理[M].北京:清华大学出版社,1998:75-76.
[3]吕映芝.语法图到产生式的自动转换[J].清华大学学报(自然科学版),1996,36(5):84-89.
[4]谭浩强.PASCAL语言程序设计[M].北京:高等教育出版社,1999:330-335.
An Improved Algorithm for First Set
XlONG Pong-rong
(School of Mathematics and Computer Science,Shangrao Normal University,Shangrao Jiangxi 334001,China)
On the[1]and[2],the and the non ultimate symbol of G are improved.The improved algorithm makes the original algorithm(n1+n2)m times,and reduces the need for n1+n2*m times.
grammar;first set;algorithm
O142
A
1004-2237(2016)03-0010-02
10.3969/j.issn.1004-2237.2016.03.003
2015-10-20
熊鹏荣(1961-),男,江西上饶人,副教授,学士,主要从事算法设计和分析研究。E-mail:xpr7810@163.com

