重力异常阶方差模型精度及其截断误差分析

常　岑，王世忠，王庆宾,3，贾　鲁，吴　亮

(1.信息工程大学 地理空间信息学院，河南 郑州 450052；2.61206部队,辽宁 大连 116023；3.63883部队，河南 洛阳 471000)



重力异常阶方差模型精度及其截断误差分析

常岑1，王世忠2，王庆宾1,3，贾鲁1，吴亮1

(1.信息工程大学 地理空间信息学院，河南 郑州 450052；2.61206部队,辽宁 大连 116023；3.63883部队，河南 洛阳 471000)

摘要：在评估重力场模型计算空间扰动引力精度时，对模型截断误差常采用阶方差方法。文中将6种经典的重力异常阶方差模型与现有超高阶重力场模型的阶方差进行比较，TSD模型与重力场模型的差值最小。根据重力异常阶方差模型TSD，文中分析不同高度、不同阶次利用重力场模型计算空中扰动引力时截断误差的影响。实验结果表明：36阶模型截断误差最大径向和水平方向分别为26.455 1 mGal、25.946 3 mGal；360阶模型截断误差最大径向和水平方向分别为9.969 0 mGal、9.960 9 mGal；2160阶模型截断误差最大径向和水平方向分别为2.538 5 mGal、2.538 1 mGal；2160阶模型计算空中扰动引力时，即使在低空附近，截断误差在2.5 mGal以内，计算高度超过5 km，截断误差可以忽略；超过400 km的高度，都可以用36阶模型计算，截断误差在1 mGal以内。

关键词：扰动引力；地球重力场模型；阶方差模型；TSD模型；截断误差

地球重力场外部变化情况是军事地球物理主要研究内容之一，利用地球重力场模型可以容易得到地球外部空间扰动引力，为远程武器和近地飞行器提供准确的制导控制依据。重力场模型的阶次越高，所描述的地球扰动引力变化情况越精细。利用重力场模型计算空中扰动引力所产生的误差主要来自两个方面：①截断误差；②重力场模型的位系数误差。一般而言，使用的重力场模型阶次越高，产生的截断误差将会越小。

目前发布的重力场模型最高阶能够到达2190阶，例如：2008年发布的EGM2008，2014年发布的EIGEN-6C4。文献[1]利用1976年Moritz计算出来的重力异常阶方差模型分析了截断误差随高度变化情况。文献[2]利用1981年RAPP计算出的重力异常阶方差模型，对不同阶次的截断误差分别进行了比较。文献[3]分析了多种重力异常阶方差模型，并利用这几种模型计算出来的重力异常阶方差的平均值作为准确值来分析重力场模型精度。文献[4]以EGM2008模型作为准确值，比较了多种重力异常阶方差模型，构建了一个新的重力异常阶方差模型—TSD模型。以上文献中，在分析截断误差时，没有考虑到不同重力异常阶方差模型的精度不同，所得到的结果不相一致的情况。本文通过比较几种重力异常阶方差模型，选出与EGM2008和EIGEN-6C4模型最为相符的重力异常阶方差模型，再对空中扰动引力截断误差进行分析。

1重力异常阶方差模型

文献[1]中用重力异常阶方差来研究截断误差对空中扰动引力的影响。球面的重力异常Δg可以用n阶重力异常来表示，则有

(1)

空中扰动引力T的截断误差ε的表达式为

(2)

其中:Cn为重力异常阶方差，ερ为径向方向的截断误差，εH为水平分量的截断误差。为了分析截断误差的大小，先要确定重力异常阶方差模型。

重力异常阶方差的位系数的表达形式如下：

(3)

其中：γ为正常重力；Cnm,Snm为正则化后的模型位系数。由于现有的模型位系数的阶数最高到2190阶，所以更高阶的阶方差只有通过构建阶方差模型来求得。Moritz在总结前人的研究成果后，给出了重力异常阶方差的通用表达形式

(4)

Jekeli和Rapp的模型均是基于此求解算出来的，表 1给出了5种经典的阶方差模型。

表1　重力异常阶方差模型

此外，国内学者翟振和等[4]根据Moritz提出的通用模型，构建了一个新的重力异常阶方差模型—TSD模型，表达式如下：

(5)

2重力异常阶方差模型精度分析

为了验证以上几种阶方差模型的精度，将它们与现有超高阶重力场模型阶方差进行比较。现有的超高阶重力场模型主要有EGM2008模型和EIGEN-6C4模型，其中EGM2008模型是现有模型中精度较高的超高阶模型，它的低阶次主要来源于GRACE卫星数据；而EIGEN-6C4模型是在2014年发布，加入了GOCE数据，从文献[5]得出来的结论可以看出，其精度较EGM2008有所提高。

从图1、图2可以看出，EGM2008和EIGEN-6C4模型阶方差基本保持一致，只有将局部放大后，才能发现二者细微的差别，所以仍然使用EGM2008模型的阶方差作为准确值与另外5种重力异常阶方差进行比较。

由图3、图4可以发现，在36阶之前的低阶部分，模型的重力异常阶方差变化比较剧烈，在36阶之后，变化越来越平缓；在低阶部分，Moritz和TSD模型的重力异常阶方差与EGM2008模型的重力异常阶方差变化更为相符。从图3、图4还可以看出，超过200阶以后，除了TSD模型，其它模型的重力异常阶方差与EGM2008相比表现出了较大的差异。

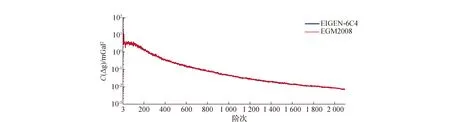
图1　EGM2008和EIGEN-6C4阶方差

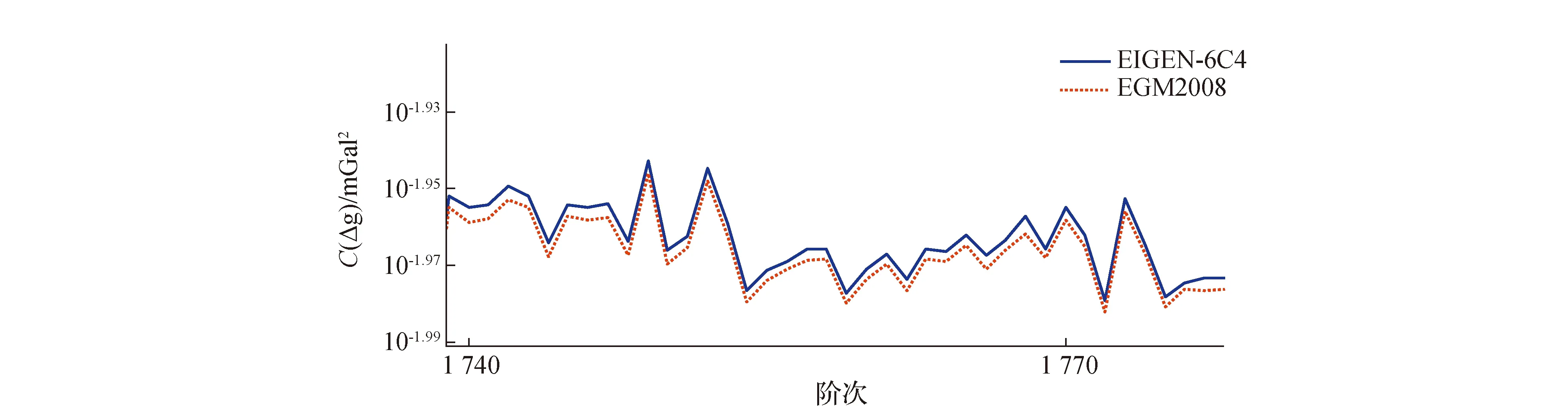
图2　EGM2008和EIGEN-6C4阶方差局部放大

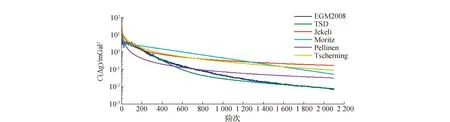
图3　EGM2008模型阶方差和6种重力异常阶方差(2100阶)

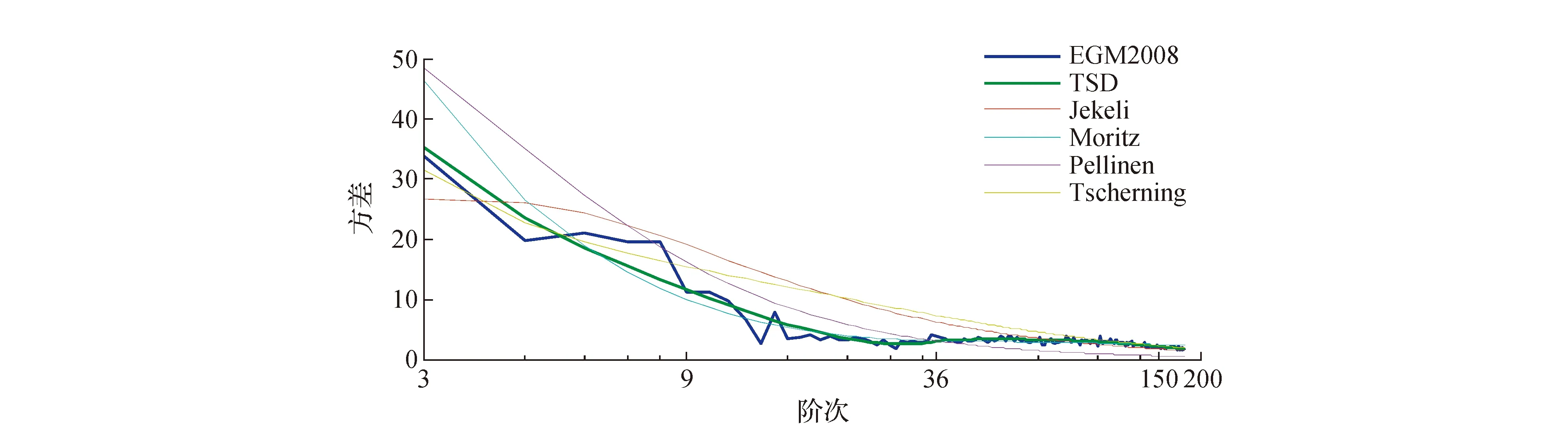
图4　EGM2008模型阶方差和6种重力异常阶方差(200阶)

从表2可以看出，Pellinen、Moritz、Jekeli 3种模型在低阶部分与EGM2008的重力异常阶方差的差值较大；超过360阶之后，它们的差值都变得非常小。其中，TSD模型与EGM2008的重力异常阶方差的差值相对其他几种模型更小。由此，可以认为TSD模型更加符合EGM2008模型的变化趋势。

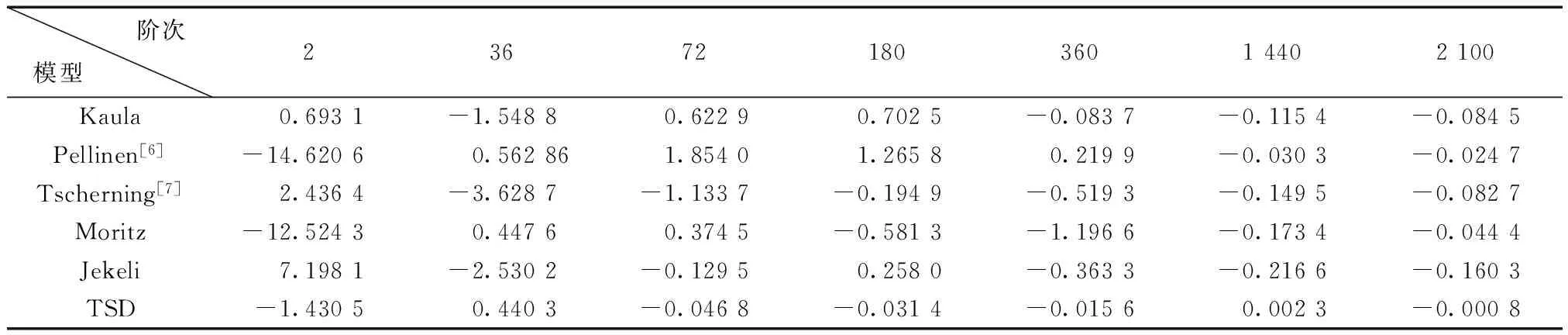
表2　EGM2008模型阶方差与6种重力异常阶方差的差值

3截断误差对扰动引力计算的影响

根据上节分析，选择TSD重力异常阶方差模型计算重力场阶方差。根据式(5)，分别计算截断到36阶、72阶、360阶、720阶、1 440阶、2 160阶时的截断误差，高度每隔1 km取一次值，计算至36 000阶。截断误差与计算点高度统计见表3。

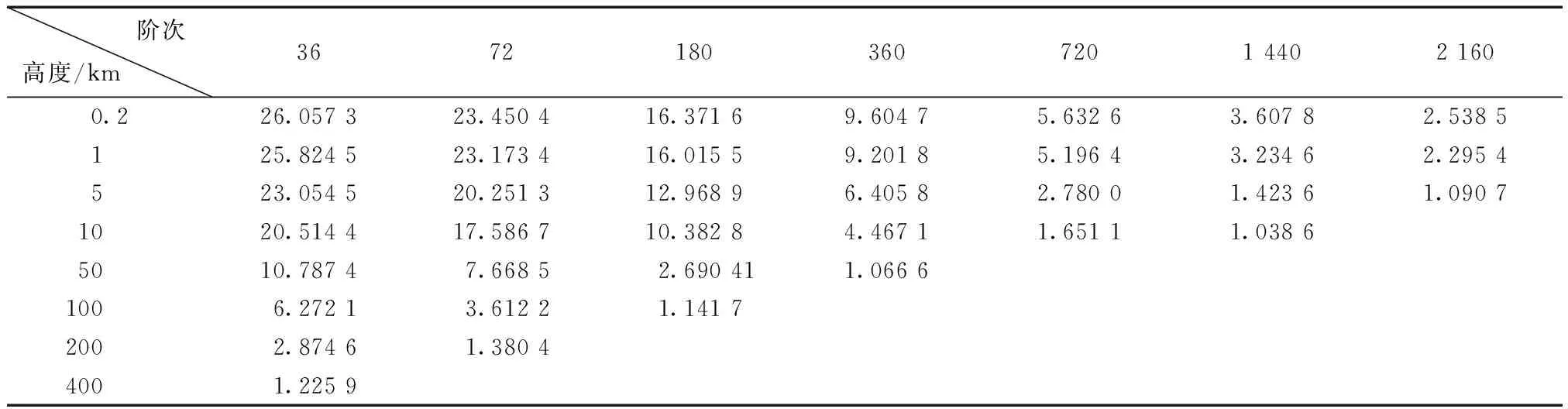
表3　截断误差与计算点高度统计(重力异常阶方差计算)

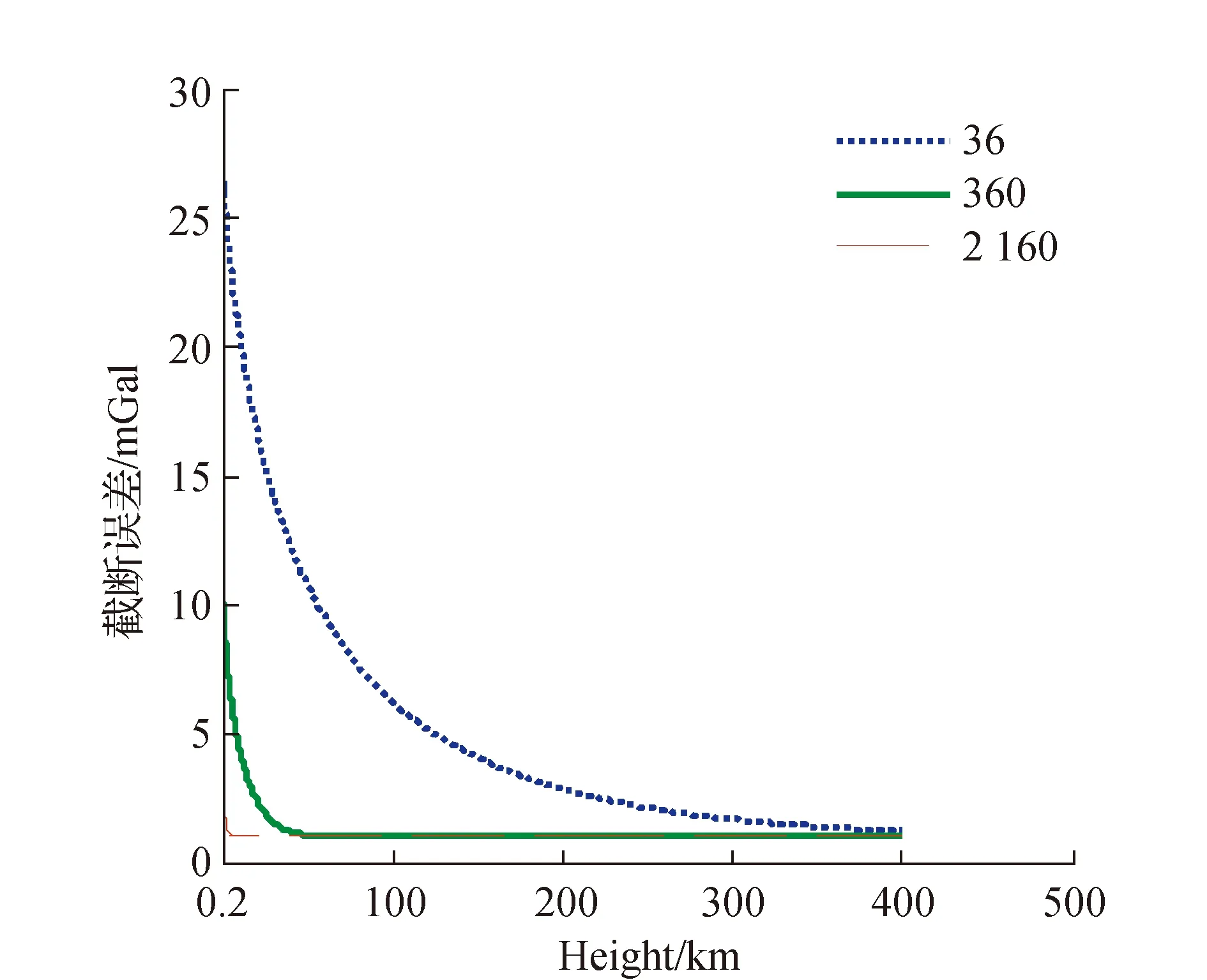
图5　模型径向方向截断误差

图6　模型水平方向截断误差

由图5、图6可以看出，模型径向和水平方向的截断误差随高度变化具有一致性，随高度增加，截断误差的影响变弱。使用36阶模型来看，在100 km以内的低空，截断误差的大小随高度急速下降；超过100 km以后，截断误差变化越来越缓慢；超过400 km，截断误差几乎不变，无限接近于1 mGal。使用2 160阶模型计算时，超过5 km的高度时，截断误差已经几乎保持不变。

4结论

利用EGM2008和最新EIGEN-6C4重力场模型分析了几种经典重力异常阶方差模型，可以得到以下结论：

1)经典的重力异常阶方差模型的高阶部分与两种超高阶重力场模型的重力异常阶方差不相符合。重力异常阶方差TSD模型在高阶部分与重力场模型的符合程度比较好。

2)利用TSD模型分析截断误差，36阶模型截断误差最大径向和水平方向分别为26.455 1 mGal、25.946 3 mGal；360阶模型截断误差最大径向和水平方向分别为9.969 0 mGal、9.960 9 mGal；2160阶模型截断误差最大径向和水平方向分别为2.538 5 mGal、2.538 1 mGal；2160阶模型计算空中扰动引力时，即使在低空附近，截断误差在2.5 mGal以内，计算高度超过5 km，截断误差可以忽略；超过400 km的高度，都可以用36阶模型计算，截断误差在1 mGal以内。

3)由于TSD模型本身的限制，使得计算截断误差时，在高阶和高空时截断误差数值收敛于1 mGal，这与实际收敛于0 mGal的情况不符。在后续研究中，有必要对于重力异常阶方差模型作进一步深入研究。

参考文献：

[1]张皞.快速逼近弹道扰动引力的算法研究[D].郑州：信息工程大学，2007.

[2]刘晓刚，吴晓平，赵东明,等.EGM96和EGM2008地球重力场模型计算弹道扰动引力的比较[J].大地测量与地球动力学，2009，29(5):62-67.

[3]KONESHOV V N，NEPOKLONOV V B，SERMYAGIN R A，et al.Modern global Earth’s gravity field models and their errors [J].Gyroscopy & Navigation，2013，4(3):147-155.

[4]翟振和，任红飞，孙中苗.重力异常阶方差模型的构建及在扰动场元频谱特征计算中的应用[J].测绘学报，2012，41(2):159-164.

[5]KONESHOV V N，NEPOKLONOV V B，SERMYAGIN R A，et al.On the estimation of accuracy for global models of gravitational field of the earth[J].Izvestiya Physics of the Solid Earth，2014，50(1):127-136.

[6]PELLINEN L P.Estimation and application of degree variances of gravity [J]，Studia Geophys.Geod.，1970，14(2):168-173.

[7]TSCHERNING C C，RAPP R H.Closed Covariance Expressions for Gravity Anomalies，Geoid Undulations，and Deflections of the Vertical Implied by Anomaly Degree Variance Models [J].Scientific Interim Report Ohio State Univ.columbus.dept.of Geodetic Science，1974.

[责任编辑：刘文霞]

DOI:10.19349/j.cnki.issn1006-7949.2016.10.008

收稿日期：2015-06-23；修回日期：2015-09-01

基金项目：国防基金(973-6132220202-2)；63880部队博士后基金

作者简介：常岑(1990-)，男，硕士研究生.

中图分类号：P223

文献标识码：A

文章编号：1006-7949(2016)10-0038-04

Analysis of degree variance of the gravity anomaly model precision and its truncation error

CHANG Cen1，WANG Shizhong2，WANG Qingbin1,3，JIA Lu1，WU Liang1

(1.School of Surveying and Mapping，Information Engineering University，Zhengzhou 450052,China;2.Troops 61206，Dalian 116023,China;3.Troops 63883，Luoyang 471000,China)

Abstract：When the precision of the gravity field disturbance is analyzed，the truncation error is the main factor which should be considered.Six classical degree variance of the gravity anomaly models are compared with the existing high-order earth gravity model.The difference between the TSD model and the earth gravity model is the smallest.According to the TSD，the influence of truncation error is analyzed when gravity field model is used to calculate the gravity of air disturbance.When using the 2160 order model to calculate the gravity of the air disturbance，even in the vicinity of the low altitude，the truncation error is within the 2.5 mGal;and when the height of the computation is over 5 km，the truncation error can be ignored;when the height of the computation is over 400 km，it can be calculated with the 36 order model and the truncation error is within 1 mGal.

Key words：disturbing gravity;earth gravity model;degree variance of the gravity anomaly;model TSD;truncation error