灰线性马尔科夫模型在建筑物变形监测中的应用
李克昭,李志伟,赵磊杰
(1.河南理工大学 测绘与国土信息工程学院,河南 焦作 454000;2.北斗导航应用技术协同创新中心,河南 郑州 450052)
灰线性马尔科夫模型在建筑物变形监测中的应用
李克昭1,2,李志伟1,赵磊杰1
(1.河南理工大学 测绘与国土信息工程学院,河南 焦作 454000;2.北斗导航应用技术协同创新中心,河南 郑州 450052)
摘要:针对传统灰色GM(1,1)预测模型在建筑物变形监测预报中的拟合精度较差、预测精度较低和预测时间较短的问题,文中以传统GM(1,1)、线性回归和马尔科夫模型为理论基础,构建了灰线性马尔科夫预测模型,并结合某建筑物变形监测的观测数据,运用新陈代谢的计算模式进行预测。结果表明,灰线性马尔科夫预测模型的拟合精度和预测精度优于单一的灰色GM(1,1)预测模型和线性回归预测模型,灰线性马尔科夫预测模型具有预测精度高、预测时间长和稳定性高的优势。
关键词:GM(1,1)模型;线性回归模型;马尔科夫模型;新陈代谢
对建筑物的变形监测分析与预报是非常必要的。变形监测的预报可用于指导建筑施工、确保施工质量和得到建筑物变形的先验信息。灰色系统理论是研究数据贫乏、资料较少、不确定性问题的理论,非常适合于建筑物的变形监测预报工作。
GM(1,1)模型是灰色理论的最简单的预测模型之一,它打破了回归分析和概率统计的局限性,以灰色生成函数为基础,以微分拟合为核心的一种建模方法。但是GM(1,1)模型在构建模型过程中受到随机数据扰动影响较大,构建的模型稳定性较差。近年来,很多学者就针对GM(1,1)模型的初值确定[1]、GM(1,1)背景值的构建[2]和GM(1,1)模型残差的修正[3-4]方面做了很多方法的尝试。但是对单一模型进行改进,对于提高预测精度相对来说是缓慢的,同时组合几个互补的预测模型可使提高预测精度达到立竿见影的效果。
线性回归预测模型[5-7]根据事物成长的规律性、事物发展的连续性以及事物因果的相关性对短时期的预测能够取得非常好的效果,但对长期预测的效果并不明显。马尔科夫预测模型的转移概率矩阵可以有效反映出随机数据的波动程度,很大程度上弥补了GM(1,1)和线性回归预测模型的局限性[8]。3种预测模型组合成灰线性马尔科夫预测模型不仅提高了预测模型的精度和适用范围,同时还能保证预测模型的稳定性。本文以传统GM(1,1)、线性回归和马尔科夫预测模型为理论基础,将提出灰线性马尔科夫预测模型,并结合某建筑物的变形监测观测资料,对组合预测模型进行验证和分析。
1灰线性马尔科夫组合预测模型的建立
1.1灰线性GM(1,1)模型
假设一组原始数据序列,记为X(0),
(1)
对数据X(0)序列进行一次累加,生成的新数据序列记为X(1),
(2)

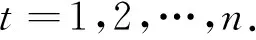
(3)
式中:a为发展系数,b为灰作用量,其形式可以记为
(4)
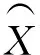
(5)
将式(5)进行累减计算得到灰线性GM(1,1)模型的拟合值和预测值。从式(5)中不难看出:当m1=0时,预测方程为线性回归方程;当m2=0时,预测方程为传统GM(1,1)预测方程。因此,灰线性GM(1,1)预测模型继承了传统GM(1,1)和线性回归的优点。
1.2灰线性马尔科夫预测模型
1)计算波动指数序列
(6)
2)划分马尔科夫状态
(7)
式(7)表示为第k对象的波动指数处于第i种状态Ei;a1i,a2i分别表示为状态Ei的上下界。因此,总的状态集合表示为
3)构造状态转移概率矩阵
(8)
式中:mij(n)为状态Ei经过n步转移到达状态Ej的次数,Mi为Ei出现的次数。由n步转移概率元素Pij(n)构成n步转移概率矩阵P(n)。
4)构造未来状态概率矩阵
(9)
式中选取离预测目标最近的s个原始对象,按照从近到远的顺序,所需的转移步数分别为1,2,…,s,分别以各个对象所对应的状态为初始状态,在n步转移概率矩阵P(n)中取各自所对应的行向量Pi(n)=[Pi1(n),Pi2(n),…,Pis(n)],i∈s,从而构成新的概率矩阵。
5)得出预测方程。
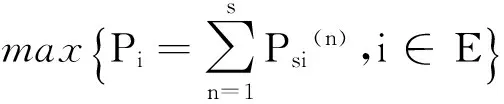
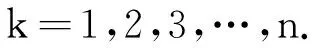
(10)
2灰线性马尔科夫预测模型精度评定
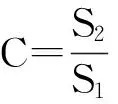

表1 预测模型精度评价[8]
3实例计算与结果分析
本文采用文献[7]中的居民楼变形监测工程数据,该工程为广州市某地产开发公司开发的新建居民楼。按照二等水准的测量规范,获得1#建筑物CJ1号点13期沉降累计观测数据。本文利用前8期沉降累计数据进行建模,分别用GM(1,1)模型、灰色线性回归模型、灰线性回归预测第9~13期沉降累计数据。CJ1号点的观测数据如表2所示。

表2 CJ1点的实测累计沉降量
3.1灰线性马尔科夫模型数据计算
文献[5-7]中表明,当建模过程中的建模期数n=8,参数m=1,2,3,4时,模型拟合精度最优。参考文献[12]的新陈代谢计算模式,用表2的前8期数据构建灰线性马尔科夫模型,预测第9期数据为例,计算过程如下:
1)利用前8期数据构建灰线性GM(1,1)模型
X(0)=[2.82,3.51,4.59,5.87,6.89,
8.37,10.99,12.59].
2)灰线性GM(1,1)模型建模生成模型拟合序列、残差序列和波动指数序列,同时计算可得第9期的预测值,如表3所示。

表3 灰线性GM(1,1)的计算结果
3)划分马尔科夫模型状态。根据表3中的波动指数划分为4种状态:E1:[-4,-2],E2:[-2,0],E3:[0,2],E4:[2,6]。
模型值所处的状态,如表4所示。

表4 模型值状态的划分
4)计算转移概率矩阵
5)计算第9期数据所处的状态。第9期状态的预测计算表如表5所示。

表5 第9期状态预测表
从表5中可得,第9期的预测状态为E4。
6)计算第9期的预测值。第9期的预测值为
3.2灰线性马尔科夫模型数据结果分析
利用Matlab7.0软件为平台,按照上述计算步骤编写程序,计算第9~13期的预测值,即:利用前8期观测数据建模,得到第9期的预测值;然后去掉建模数据中第1期数据,加入第9期的预测值重新建模,计算第10期的预测值;依次类推,计算出第9~13期的预测值;最后,求取新陈代谢过程中所产生的拟合值和预测值的平均值,作为灰线性马尔科夫模型的拟合值和预测值。其计算结果和分析如下:
1)GM(1,1)、灰线性GM(1,1)、灰线性马尔科夫3种模型的拟合值和预测值见表6、表7。

表6 3种预测模型拟合值结果 mm
从表6得出,灰线性马尔科夫的模型拟合残差中误差0.030 2mm,灰线性GM(1,1)模型的拟合残差中误差0.233 5mm,传统的GM(1,1)模型的拟合残差中误差0.569 1mm。灰线性马尔科夫组合模型的拟合精度优于前两种预测模型。
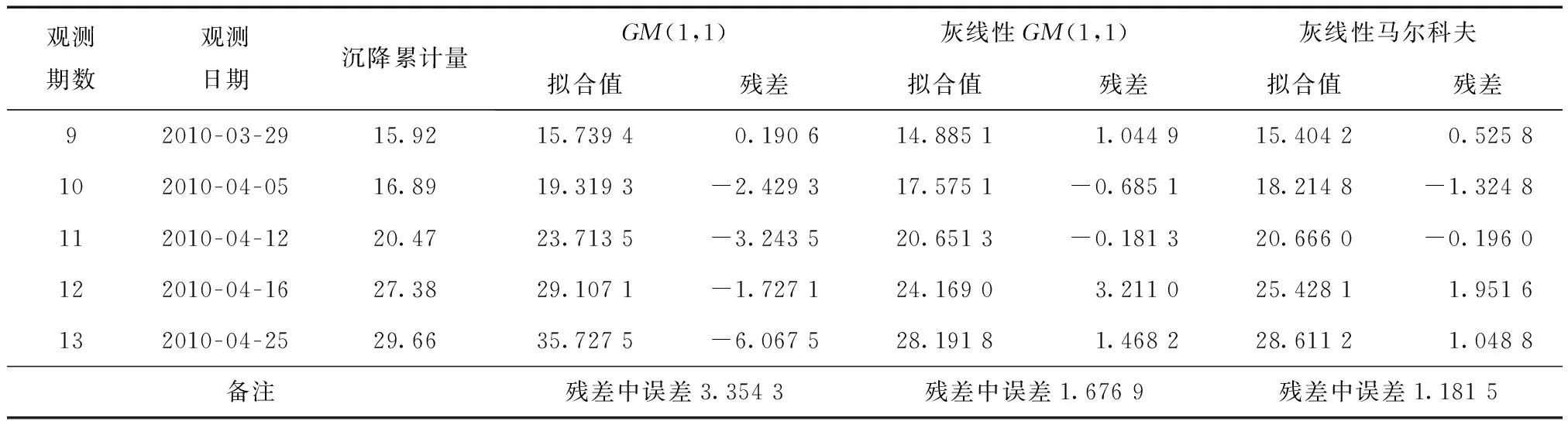
表7 3种预测模型预测值结果 mm
从表7中得到,灰线性马尔科夫预测模型的预测值残差中误差1.181 5mm,灰线性GM(1,1)预测模型的预测值残差中误差1.676 9mm,传统GM(1,1)预测模型的预测值残差中误差3.354 3mm。灰线性马尔科夫组合模型的预测精度优于前两种预测模型。
2)GM(1,1)、灰线性GM(1,1)、灰线性马尔科夫3种模型的相对误差见表8。
相对误差更能直观反映出模型的相对精度,区分出模型精度的优劣。

从表8和图1中可以看出,无论是拟合值还是预测值,灰线性马尔科夫预测模型均优于灰线性GM(1,1)预测模型和传统GM(1,1)预测模型。因此,灰线性马尔科夫预测模型更加准确,外推的预测值更多,外推的预测值更可靠,模型更加稳定。
3)GM(1,1)、灰线性GM(1,1)、灰线性马尔科夫3种模型的精度评定见表9。

表8 3种预测模型的相对误差结果

图1 3种预测模型相对误差比较

传统GM(1,1)灰线性GM(1,1)灰线性马尔科夫P111C0.07450.07070.0149
经计算,传统GM(1,1)预测模型的小残差概率P=1,方差比C=0.074 5;灰线性GM(1,1)预测模型的小残差概率P=1,方差比C=0.070 7;灰线性马尔科夫预测模型的小残差概率P=1,方差比C=0.014 9。由于所选取的数据变化比较平滑,所以3种预测模型精度结果皆为优。但是从方差比可以看出,灰线性马尔科夫预测模型精度优于前两种预测模型。
4结束语
本文综合传统GM(1,1)模型、线性回归模型和马尔科夫模型的优点,构建了灰线性马尔科夫预测模型,运用新陈代谢的计算模式对建筑物变形监测进行预测。得出的结论为:灰线性马尔科夫预测模型无论是拟合精度还是预测精度都要优于单一的灰色GM(1,1)预测模型和线性回归预测模型,灰线性马尔科夫预测模型具有预测精度高、预测时间长和模型稳定性高的优势。
对于变形监测工作中实测的观测数据建立合适的预测模型。在满足工程应用的精度要求下,预测模型需要的观测资料较少,减轻了大量的外业实测工作,提高了工作效率,同时提供了可靠的参考资料。本文建立的灰线性马尔科夫预测模型,为了保证预测模型的可靠性,建议建模数据不要低于6期实测数据,同时建议连续外推的预测值不要超过5期为宜。
参考文献:
[1]张彬,西桂权.基于背景值和边值修正的GM(1,1)模型优化[J].系统工程理论与实践,2013,33(3):682-688.
[2]袁豹,岳东杰,李成任.基于总体最小二乘的改进GM(1,1)模型及其在建筑物沉降预测中应用[J].测绘工程,2013,22(3):52-55.
[3]李秀珍,孔纪名,王成华.灰色GM(1,1)残差修正模型在滑坡预测中的对比应用[J].山地学报,2007,25(6):741-746.
[4]郭兰兰,邹志红,安岩.基于残差修正的GM(1,1)模型在水质预测中的应用[J].数学的实践与认识,2014,44(19):176-181.
[5]高宁,崔希民,高彩云.高层建筑物沉降变形的灰线性预测[J].测绘科学,2012,37(3):96-98.
[6]陈怀争,王勇.灰色线性回归组合模型在变形监测数据处理和预测中的应用[J].资源与产业,2011,13(增1):165-167.
[7]张俊中,雷伟伟,王睿,等.灰线性回归模型在建筑物沉降分析中的应用[J].河南科学,2015,33(3):416-420.
[8]王磊,武术静,李长青.灰色马尔科夫模型对煤自燃发火预测的研究[J].河南理工大学学报(自然科学版),2015,34(1):35-39.
[9]杨灿,杨敏华,汪奇松.基于灰色马尔科夫链预测系统的设计与实现[J].测绘通报,2009(6):182-183.
[10] 沈哲辉,黄腾,唐佑辉.灰色-马尔科夫模型在大坝内部变形预测中的应用[J].测绘工程,2015,24(2):69-74.
[11] 杨锦伟,孙宝磊.基于灰色马尔科夫模型在平顶山市空气污染物浓度预测[J].数学的实践与认识,2014,44(2):64-70.
[12] 岳仁宾,腾德贵,胡波,等.灰色模型在深基坑变形监测中的应用研究[J].测绘通报,2014(S1):85-87.
[责任编辑:刘文霞]
DOI:10.19349/j.cnki.issn1006-7949.2016.10.002
收稿日期:2015-06-26
基金项目:国家自然科学基金资助项目(41202245;41272373);河南理工大学骨干教师资助项目(72105/090)
作者简介:李克昭(1977-),男,副教授,博士.
中图分类号:TV698.1
文献标识码:A
文章编号:1006-7949(2016)10-0005-05
Application of grey line Markov model to the deformation monitoring of buildings
LI Kezhao1,2,LI Zhiwei1,ZHAO Leijie1
(1.School of Surveying and Landing Information Engineering,Henan Polytechnic University,Jiaozuo 454000,China;2.Collaborative Innovation Center of BDS Research Application,Zhengzhou 450052,China)
Abstract:Traditional gray GM (1,1) predicting model has the problems of poor fitting accuracy,lower prediction accuracy and shorter prediction time in deformation monitoring and forecasting of buildings.In this paper,a combination of the traditional GM (1,1) model,linear regression and Markov model is constructed of grey linear Markov model.Combined with observations data of the deformation monitoring of buildings,the metabolism computing model is used to predict.The results show that:the fitting accuracy and model prediction accuracy of the linear Markov model gray model are better than a single gray GM (1,1) forecast model and linear regression forecasting model.Gray linear Markov model has the advantages of high accuracy,long time and high stability of prediction.
Key words:GM(1,1) model;linear regression models;Markov model;metabolism

