钢筋混凝土轴心受压T形柱力学性能研究

李佩，刘忠，李科锋，陈叶

（湘潭大学土木工程与力学学院，湖南 湘潭 411105）

钢筋混凝土轴心受压T形柱力学性能研究

李佩，刘忠，李科锋，陈叶

（湘潭大学土木工程与力学学院，湖南 湘潭 411105）

针对钢筋混凝土轴心受压T形柱的受力性能，采用有限元分析技术进行非线性数值模拟，计算值与试验值吻合较好，表明论文建立的三维有限元模型是合理的。利用该模型，探讨长细比、混凝土强度、纵筋配筋率、箍筋配箍率等参数对试件力学性能的影响。

T形柱;轴心受压;力学性能

1 引言

异形柱通常是指钢筋混凝土框架结构中截面形状为L形、T形和十字形的柱体。采用异形柱，可扩大建筑有效使用面积，提高建筑布置灵活性，改善室内空间视觉效果。因此，异形柱特别适合住宅建筑，许多省市的住宅建筑中已有广泛的应用。

国内外学者对异形柱已有较为深入的研究，包括运用计算机进行数值分析[1,2]、试验研究和理论分析等[3,4]。

本文针对钢筋混凝土轴心受压T形柱的受力性能，采用有限元分析技术进行数值模拟，探讨长细比、混凝土强度、纵筋配筋率、箍筋配箍率等参数对试件力学性能的影响。

2 有限元模型

2.1 试验简介

针对钢筋混凝土异形柱的受力特性，孙林柱等人[5]进行了一系列试验研究。本文取其中ZT6进行研究，柱高为，试件尺寸及截面配筋如图1所示。

图1 试件尺寸及截面配筋图

2.2 模型建立

根据试验过程，本文取柱子T形部分建立模型，柱两端设置厚度为30mm刚性垫块。

T形截面形心坐标为X=135mm，Y=99mm。因此，建模时设坐标原点位于柱底形心处，X轴设在翼缘方向，Y轴设在腹板方向，沿柱高为Z轴方向。核心混凝土应力-应变关系取改进的Kent—Park模型[6]；钢筋选用理想弹塑性本构关系。

钢筋骨架与混凝土采用内置区域的方式；T形柱与垫块间绑定连接；在2垫块外表面T形柱形心处建立参考点，分别与垫块表面进行耦合，并在参考点施加位移荷载。对于轴压短柱试件，一端设为固定约束，另一端放开轴向自由度。所得模型如图2所示。

图2 有限元模型

将有限元分析得到试件的荷载-应变曲线、极限承载力（曲线中荷载最大值）以及峰值应变（曲线峰值点处应变）与试验结果进行对比，分别如图3和表1所示。

图3 计算值与试验值对比图

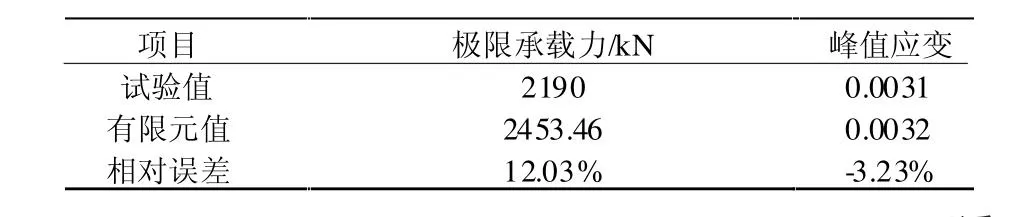
表1 有限元结果与试验结果比较

由图3可知，2条曲线在上升段趋势相同，且较为靠近；从表1中数据得出，极限承载力误差为12.03%，峰值应变误差为-3.23%，误差均在允许范围内。由此说明,本文建立的钢筋混凝土轴心受压T形柱有限元模型是合理的。

3 受力性能分析

3.1 截面应力分析

图4为沿柱高不同截面混凝土纵向应力分布图。由图可知，混凝土横向膨胀使箍筋产生弯曲，箍筋的约束作用最强位置在箍筋转角部位，最弱位于直线段中部附近，这种作用使箍筋所在平面形成“拱”，与保护层间形成弱约束区，应力值较小；截面中央为强约束区，应力值较大。由圣维南原理，靠近柱端截面应力值较大于柱中截面；同一截面中，不同位置应力值差别不大，且各截面应力值近似相等，均为负值，说明混凝土近似处于均匀压缩状态。图5为柱中截面钢筋纵向应力分布图，所有钢筋应力相等，说明钢筋处于均匀压缩状态。故由图4、图5得出，在轴心荷载作用下，试件处于压缩状态，且各截面的应力分布较为均匀。

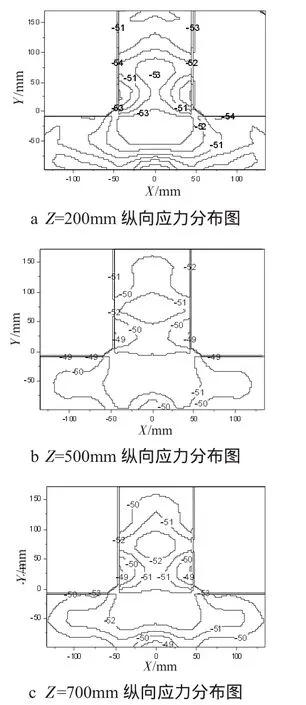
图4 不同截面混凝土纵向应力分布图

图5 Z=500mm钢筋纵向应力分布图

3.2 截面应变分析

图6为混凝土N-ε关系曲线。由图可知，加载初期，纵向应变与环向应变均呈线性变化，但纵向应变曲线斜率大于环向，说明材料在弹性范围内变化，且试件纵向应变大于环向应变；当试件进入弹塑性阶段，材料纵向进入强化阶段，环向进入塑性阶段。由此得出，在轴心荷载作用下，试件纵向先发生破坏，然后环向发生破坏。

图6 混凝土N-ε关系曲线

3.3 参数分析

3.3.1 长细比

图7为不同长细比荷载-纵向位移曲线。由图可知，随着长细比的增加，试件极限承载力减小，纵向位移增加。这是由于试件越长，纵向刚度越小，纵向位移也越大，说明试件的延性性能越好。

图7 荷载-纵向位移曲线

根据异形柱规范[7]，λ≤17.5即认为是短柱。图8为λ=10和λ=62的试件沿柱高横向应变图，由图可知，λ=10的短柱破坏形态为柱中鼓曲呈灯笼状破坏；λ=62的中长柱破坏形态为上下各1/4处鼓曲呈哑铃状破坏。这说明柱高度较小时，由于上下两端受力后，力有效地向中部传递，使得柱中部位荷载较大，最终呈灯笼状破坏；当柱高度较大时，两端作用力向中间传递时，由于两端柱面上存在较大的摩擦力，且柱身高度较大，荷载不能有效传递到柱身中部，所以在柱身上下各1/4处出现鼓曲破坏，试件最终呈哑铃状破坏。

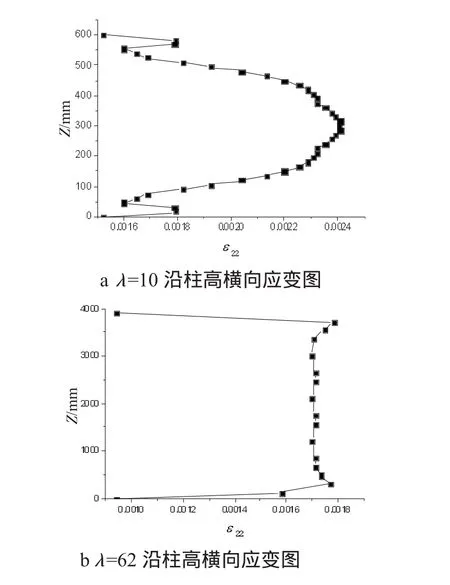
图8 不同长细比试件沿柱高横向应变图

3.2.2 混凝土强度

图9为不同混凝土强度荷载-纵向位移曲线。由图可知，随着混凝土强度的增加，钢筋混凝土T形柱的刚度增加，承载力提高，相应的纵向位移减小。

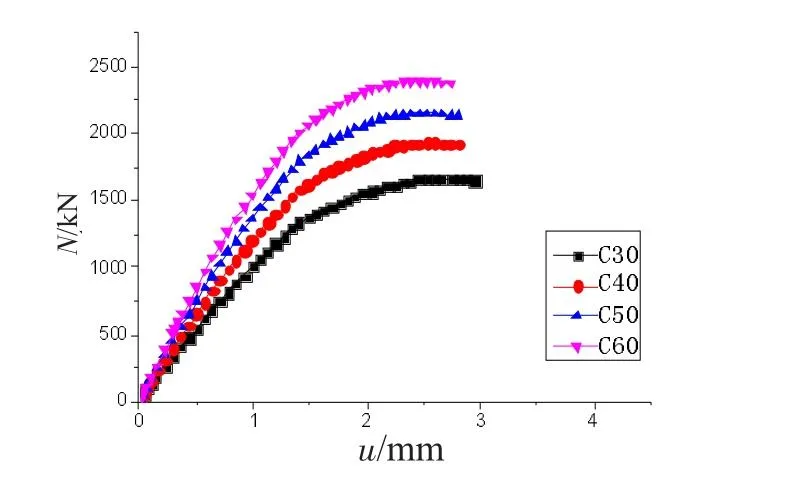
图9 荷载-纵向位移曲线

图10 不同纵筋配筋率荷载-纵向位移曲线

3.3.3 纵筋配筋率

图10为不同纵筋配筋率荷载-纵向位移曲线。由图可知，随着纵筋配筋率的增加，钢筋混凝土T形柱的承载力相应提高，但试件的纵向位移几乎相同，说明配筋率的提高，对纵向位移的影响很小。

3.3.4 体积配箍率

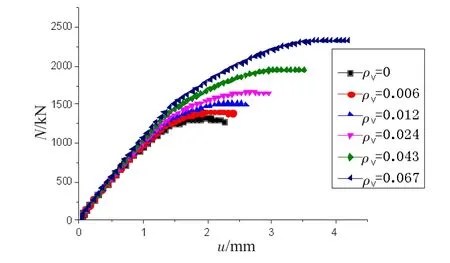
图11 不同体积配箍率荷载-纵向位移曲线

图11为不同体积配箍率荷载-纵向位移曲线。由图可知，50%～60%峰值承载力以前，曲线基本重合，说明此阶段，箍筋的约束作用较小；50%～60%峰值承载力以后，随着荷载的增加，箍筋的约束作用增强。随着体积配箍率的增加，钢筋混凝土轴心受压T形柱的峰值承载力和对应的纵向位移增大。

4 结语

1）随着长细比的增加，试件的极限承载力减小，纵向位移增大。

2）长细比较小的试件呈灯笼状破坏，长细比较大的试件呈哑铃状破坏。

3）随着混凝土强度的增加，试件的刚度增加，承载力提高，相应的纵向位移减小。

4）随着纵筋配筋率的增加，试件的承载力相应提高，但纵向位移几乎相同。

5）箍筋约束作用主要发生在50%～60%峰值承载力以后，随着体积配箍率的增加，钢筋混凝土轴心受压T形柱的峰值承载力和对应的纵向位移增大。

【1】JoaquinMarin.DesignAidsforL-ShapedReinforcedConcreteColumn [J].JournalofAmericanConcrete Institute，1979，76(11)：1197-1216.

【2】Cheng-Tzu TomasHsu.T-ShapedReinforcedConcreteMembersunder BiaxialBendingand AxialCompression[J].ACIStructuralJournal，1989(4)：46.-468.

【3】陈云霞，刘超，等.T形、L形截面钢筋混凝土双向压弯构件正截面承载力的研究[J].建筑结构，1999（1）：11-15.

【4】冯建平，陈谦.L形和T形截面柱正截面承载力的研究[J].华南理工大学学报，1995（1）：51-61.

【5】孙林柱.钢筋混凝土异形柱轴心受压性能的试验研究[D].天津：天津大学，2006.

【6】ParkR，Negel PMM J，Wayne D G.Ductility of square-confined concretecolumns[J].StructureDir，ASCE，1982，108（ST4）：929-950.

【7】JGJ149—2006混凝土异形柱结构技术规程[S].

The Research on Mechanical Properties of T-shaped Concrete Column Under Axial Loading

LI Pei，LIU Zhong，LI Ke-feng，CHEN Ye
(College of CivilEngineeringandMechanics，XiangtanUniversity，Xiangtan 411105，China)

In view of the mechanical properties of T-shaped concrete column under axial loading，using the finite element analysis technology to carryoutnonlinearnumericalsimulation，thecalculated resultsareagreedwellw ith theexperimentalones.The resultsshow that the 3D finite element analysis model is reasonable.Using this model，studying the influence on mechanical properties of slenderness ratio、concretestrength、theratioof longitudinalreinforcement、stirrup reinforcementratioofcolumn.

T-shaped column;axialloading;mechanicalproperties

TU375

A

1007-9467（2016）08-0041-04

10.13616/j.cnki.gcjsysj.2016.08.005

2016-02-28

李佩（1990～），女，陕西西安人，在读硕士，从事结构工程研究，（电子信箱）578707530@qq.com。