动载作用下典型沥青路面剪应力特性分析
肖 川,艾长发,邱延峻
(1.四川建筑职业技术学院,四川 德阳 618000;2.西南交通大学 土木工程学院,四川 成都 610031;3.西南交通大学 道路工程四川省重点实验室,四川 成都 610031)
动载作用下典型沥青路面剪应力特性分析
肖川1,3,艾长发2,3,邱延峻2,3
(1.四川建筑职业技术学院,四川德阳618000;2.西南交通大学土木工程学院,四川成都610031;3.西南交通大学道路工程四川省重点实验室,四川成都610031)
摘要:为探究动态荷载作用下沥青路面的剪应力响应特征,应用ABAQUS建立半刚性路面(S1)、倒装式路面(S2)、组合式路面(S3)的动力有限元分析模型,针对3类典型沥青路面的剪应力空间分布特性,动、静剪应力差异以及路面结构和车辆荷载参数对剪应力的影响规律等方面开展数值模拟分析。研究结果表明:沿路面深度方向,剪应力最大值位于中面层顶面位置(40 mm深度处);剪应力在水平面的分布主要集中在车轮荷载作用区域,最大值位于轮印边缘位置处;S2的剪应力最大,S1与S3的剪应力较为接近,S3略大于S1;相比于静态荷载,动荷载作用下的剪应力更大,二者的差异性随轴重水平提高逐渐增大;剪应力随基层模量增加而减小,随面层模量的增大而增大,随基层厚度增加逐渐减小;随着车速和轴重的提高,路面剪应力均逐渐增大;剪应力随轴距增加呈先增大后减小的趋势,在轴距取1.1 m时,剪应力出现最大值;随着行车加速度的增加,路面剪应力基本呈线性关系增大,轴重与车速的提高,均会增大沥青路面在车辆制动过程中的剪应力。
关键词:道路工程;沥青路面;三维有限元分析;剪应力;动荷载
0引言
随着国民经济日益发展,公路运输对于高速、重载的要求与日俱增,高等级沥青路面在使用过程中暴露出寿命不足、早期病害严重等缺陷。其中,由于路面抗剪切能力不足所产生的路面推移、拥包以及流动性或压密性车辙问题[1],是沥青路面使用过程中的显著病害。因此,研究沥青路面的剪应力特性,对合理解释路面损坏原因,保障路面使用寿命具有重要意义。
我国现行沥青路面设计规范[2]将车辆荷载视为均布竖向静态荷载,与实际行车荷载间存在较大差异,此外在控制和验算指标选取时,未对剪应力指标作出明确规定;文献[3-4]采用路面结构有限元法模拟了剪应力在沥青路面结构中的分布情况;文献[5]考虑荷载影响作用,研究了超载状态下路面剪应力的变化规律;文献[6]针对半刚性基层沥青路面研究了最大剪切应力的大小和位置。但以上研究都是基于静力学理论的“理想化”分析结果,与动载模式下的实际力学响应存在较大差异。文献[7]分析了半正弦荷载作用下,温度及深度因素对沥青路面剪应力的影响规律,但其研究过程未考虑水平荷载的影响作用。文献[8]对沥青路面的动态剪切响应进行了研究,得出了刹车反复作用下沥青路面的力学行为特征,但在模型构建时将路面各结构层视为完全连续,忽略了层间接触状态对路面抗剪性能的影响。
鉴于此,本研究以商业通用有限元软件ABAQUS为平台,研究了半刚性(S1)、倒装式(S2)和组合式(S3)3种典型沥青路面内部动态剪应力的空间分布特性,并通过动、静剪应力对比,明确了路面动力行为分析的重要性。在此基础上,进一步分析了路面结构参数及车辆荷载参数对剪应力的影响规律,以期为探究路面损坏机理提供参考。
1沥青路面结构动力有限元模型
1.1路面结构基本模型
参考文献调研结论并结合试算验证,以计算结果收敛稳定为依据,拟定路面结构的平面尺寸为6 m×6 m,路基计算深度取6 m。路面结构和其荷载形式具有对称性,为提高运算效率,取1/4模型进行分析。边界条件为:路基底面(z方向)固定、各结构层对称面施加对称约束、侧面(x和y方向)分别施加水平约束[9-10],其中x和y方向分别表示道路横向和纵向,有限元模型中各结构层采用八节点六面体完全积分单元C3D8模拟。路面结构有限元基本模型如图1所示。

图1 路面结构有限元模型(1/4模型)Fig. 1 Finite element model of pavement structure (1/4 model)
1.2荷载参数
考虑到行车荷载模式的复杂性,以固定位置(车胎与路表接触面)的冲击荷载作为路面简化荷载场,将轮印区域视为当量圆,并假设接触压力均匀分布。车辆静止时,轴载采用恒定静载模式;对于动态荷载,其荷载集度变化参考Yang H. Huang在KENLAYER程序中的简易方法[11],荷载强度随时间呈半正弦函数变化(图2),具体荷载模型见式(1)。
(1)
式中,q为荷载强度峰值,标准轴载取0.7 MPa;T为动荷载作用周期;R为轮胎与地面的接地当量圆半径,标准轴载取0.106 5 m。

图2 动荷载强度变化Fig.2 Variation of dynamic load strength
对于动态荷载模式,其荷载作用时间取决于行车速度v和轮胎接触面半径R,根据KENLAYER计算程序假设[11],荷载作用周期T的计算见式(2):
(2)
式中符号同上。
在具体计算中,为降低网格划分的难度,并提高网格的质量,将轮印面积简化为与当量圆面积相等的矩形面积[11](图3)。以单轴双轮组100 kN荷载作为标准轴载,根据图3所示矩形的长宽比,每个矩形轮印尺寸为:长a=22.78 cm(行车方向),宽b=15.68 cm,如图4所示。

图3 轮印面积简化图形Fig. 3 Simplified graphics of tire impression area

图4 标准轴载荷载分布图示(单位:cm)Fig. 4 Diagram of standard axle load distribution (unit: cm)
1.3路面结构组合材料参数
参考国内外沥青路面结构的主导形式[12],以半刚性路面(S1)、倒装式路面(S2)和组合式路面(S3)3类典型沥青路面结构作为研究对象开展动力分析,如表1所示。

表1 路面结构组合
对于路面材料的动态模量而言,相同材料的模量值在不同荷载、温度、湿度等因素影响下的变化范围较大,本次计算参考沥青路面材料动态力学参数的取值范围[12],以车速80 km/h(作用时间0.058 s)为标准条件,从中选取代表值作为模型计算参数。此外,在实际路面结构中,由于工序间隔、施工污染及各结构层材料属性差异等因素,沥青路面各结构层的层间界面之间很难做到完全黏结,即通常处于部分连续状态,因此采用以层间摩阻系数μ表征的接触模型更有助于获取路面结构内部的真实应力传递规律[13]。具体计算参数设置见表2。

表2 路面结构计算参数
注:表中μ值分别对应不同结构层之间的摩阻系数,其中上面层与中面层间、中面层与下面层间,μ取0.7;下面层与基层间、基层与底基层间,μ取0.5;底基层与路基之间为绑定连接(Tie)。
分析过程考虑阻尼影响作用,首先通过模态分析,获取结构模型在主振方向(z方向)的振型及自振频率,然后将路面结构阻尼比ζ设定为0.05[15],通过第一、二阶自振频率ω1,ω2与结构阻尼ζ确定相应的Rayleigh阻尼分项系数α=5.159和β=3.622×10-4,如式(3)所示:
(3)
2剪应力特性分析
2.1剪应力空间分布特性
计算中车辆轴重取标准轴载BZZ-100,行车速度80 km/h(对应的荷载作用周期为0.058 s),空间坐标(图5)以轮轴中心为原点O。道路横向为x轴,行车方向(纵向)为y轴,厚度方向为z轴。考虑到面层内部最大剪应力的方向变化复杂,不宜用直观方式表示,因此难以准确评价剪应力所对应的路面破坏模式,本文取水平纵向(y方向)剪应力分析计算路面剪切状态,对应评价沥青路面由于纵向流动剪切引起的推移、拥包及车辙病害。

图5 空间坐标系Fig. 5 Space coordinate system
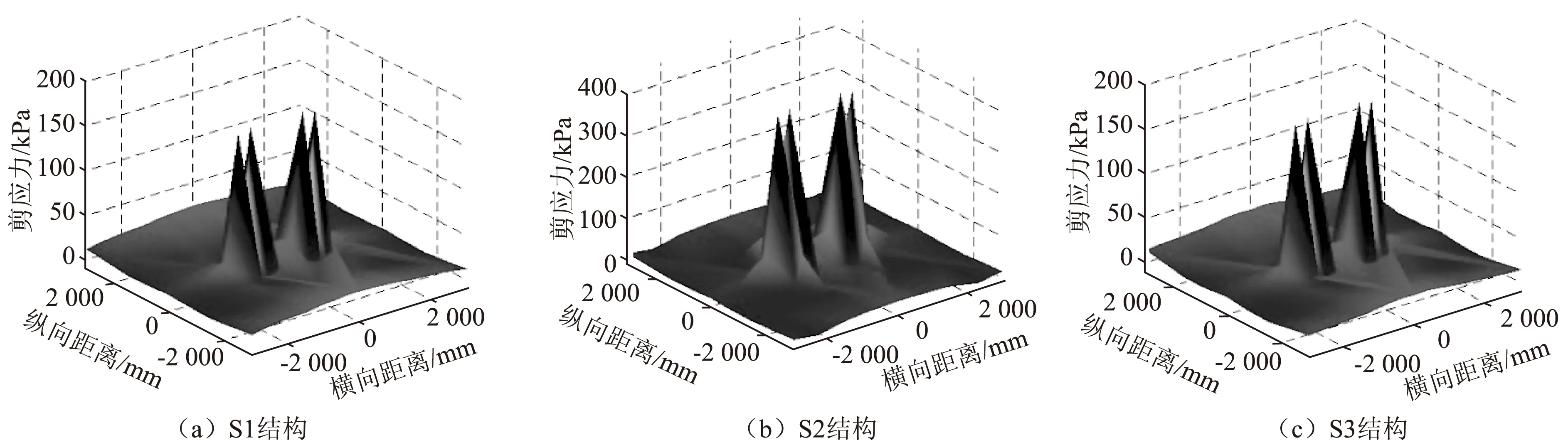
图7 剪应力三维分布图Fig.7 Three-dimensional distribution of shear stresses
图6为路面内部剪应力在内侧轮印中心位置处随道路深度的变化情况。3种路面结构的剪应力最大值均出现在上面层与中面层之间(40 mm深度),中面层顶面位置。其中,S2结构的剪应力最大值是S1和S3结构的2倍以上,因此更容易出现推移、拥包等破坏现象。此外,由于S2结构采用级配碎石作为基层材料,与面层沥青混合料材料性能差异较大,剪应力在面层与基层之间(下面层底面与基层顶面间)发生急剧突变。
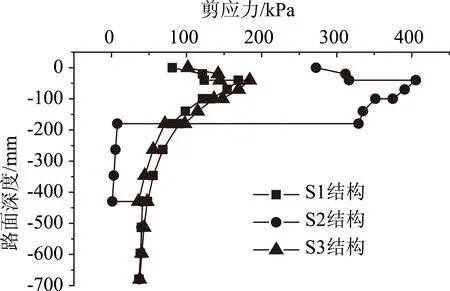
图6 剪切应力沿路面厚度的分布Fig.6 Distribution of shear stresses along pavement thickness
图7为剪应力在沿路面厚度方向的最不利位置——中面层顶面的分布情况,剪应力主要集中在车轮荷载作用处,轮印区域的剪应力较轮隙处存在突变,剪应力大小随着与荷载作用点的纵、横向距离增加而急剧减小。
图8为剪应力沿道路纵向及横向的分布情况,通过对比发现,剪应力的最大值并非出现在轮印中心位置,往往出现在轮印边缘位置处。3种路面结构的剪应力大小关系为:S2结构的剪应力最大,而S1与S3结构的剪应力较为接近,S3略大于S1结构。

图8 中面层顶部的剪应力分布情况Fig.8 Distribution of shear stresses at top of mid-surface
2.2动、静剪应力对比
基于前文建立的沥青路面结构3D有限元模型,针对3种典型沥青路面开展动、静剪应力对比分析,如图9所示。其中,柱状图分别对应不同荷载下的静力与动力响应量,图中带数据标记的折线表示路面结构动、静剪应力比值随轴重的变化。

图9 路面动、静剪应力响应对比Fig. 9 Comparison between dynamic and static shear stress responses in pavement

图10 模量对剪应力的影响Fig.10 Influence of modulus on shear stress
由图9可以看出,路面结构的动、静剪应力均随轴重的增加逐渐增大,但其大小差异明显:相比于静态荷载,动载作用下的路面结构在力学性质上表现出模量值增大,其剪应力的动力响应明显大于静力响应。若以动力修正系数μd(μd=Rd/Rs)表示各力学指标动力响应Rd与静力响应Rs的定量比值关系,剪应力的动、静力响应比值范围为1.2~2.3,其中S1与S3接近,比值范围为1.2~1.7;S2为1.6~2.3。在相同路面结构中,动、静剪应力之比随轴重的增加呈逐渐增大的趋势,表明随着轴重水平的提高,动态与静态荷载模式所引起的剪应力差异有所增大。
沥青路面动、静剪应力的差异性表明,为了更加有效地抑制路面早期剪切病害,并对其使用性能的及时修复做出合理决策,应采用反映实际交通荷载下路面结构力学行为的动力分析方法,开展路面分析与设计工作。
2.3路面结构参数对剪应力的影响
2.3.1材料模量对动力响应指标的影响
参考典型路面结构层的经验厚度(面层18 cm+基层30 cm+底基层20 cm),结合各结构层材料动态模量值的变化范围,以面层模量(4水平)与基层模量(5水平)为变化参数(如表3所示),沥青层剪应力随路面材料模量的变化规律如图10所示。

表3 材料模量组合
注:组合式路面的面层与基层均为沥青类结构层,其基层模量水平的选取通过基层与面层的模量比值进行控制。
由图10可知3种路面具有相似的变化规律:剪应力随基层模量增加逐渐减小,随面层模量的增大逐渐增大。比较不同面层或基层模量水平下剪应力值的变化幅度发现:随面层模量水平提高,S1与S3中剪应力随基层模量增大而减小的幅度增大,而S2中的变化幅度有所减小;随基层模量水平提高,S1与S3中剪应力随面层模量增加而增大的幅度有所减小,而S2中的变化幅度有所增大。这表明,在S1和S3中,面层模量水平越高,通过提高基层模量减小路面剪应力的效果越明显,而基层模量水平越低,通过降低面层模量减小路面剪应力的效果越明显;与之相反,在S2中,面层模量水平越低,提高基层模量对减小剪应力的效果越明显,基层模量水平越高,降低面层模量对减小剪应力的效果越明显。
2.3.2基层厚度对动力响应指标的影响
在沥青路面结构设计过程中,结构厚度是一项重要的设计参数。考虑到沥青面层材料要求严、造价高的特点,分析中根据经验采用典型面层厚度,而将基层厚度作为路面结构厚度变量。以半刚性路面为代表性结构,基层厚度分别取10,20,30,40 cm及50 cm,剪应力随基层厚度的变化情况如图11所示。
由图11可知,剪应力随基层厚度增加逐渐减小,而随着基层厚度的增大,其递减速率呈逐渐减小的趋势。以基层模量取8 000 MPa为例,当基层厚度由10 cm增加至20 cm时,沥青层剪应力减小了15.5%,随着基层厚度水平逐渐升高,当其厚度由40 cm增至50 cm时,剪应力仅减小了5.0%。这表明,当基层厚度较大(>40 cm)之后,通过提高基层厚度来改善路面抗剪性能的效果明显减弱。

图11 基层厚度对剪应力的影响Fig.11 Influence of base thickness on shear stress
2.4车辆荷载参数对剪应力的影响
2.4.1车速、轴重及轴距对剪应力的影响
以半刚性路面(S1)为标准模型,不同行车速度、轴重及轴距条件下,剪应力的时程曲线分别如图12(a)~(c)所示。

图12 车速、轴重与轴距对剪应力的影响Fig.12 Influence of vehicle speed, axle load and wheelbase on shear stress
由图12(a)可知,车速对剪切应力有较大影响,随车速提高,剪应力逐渐增大,车速120 km/h时的剪应力较20 km/h增加了20.46%。由此可推断,在车辆运行过程中对超速现象进行控制,是避免沥青路面在车辆荷载作用下产生剪切类病害的有效途径。
由图12(b)可知,随着荷载轴重的增加,车辆作用与路面上的动荷载效应逐渐增大,在整个加载时程内,路面剪应力有显著提高,当轴重超载160%(荷载260 kN)时,剪应力峰值增加90.2%。
由图12(c)可知,以1.1 m轴距为分界点,剪应力随轴距增加呈先增大后减小的趋势,轴距取1.1 m 时,剪应力出现最大值,对沥青层抗剪最为不利。当轴距≥1.4 m之后,剪应力响应与单轴标准轴载基本相等,且轴距变化对剪应力的影响作用较小。
2.4.2考虑水平荷载效应的剪应力分析
在车辆与路面相互作用过程中,不仅产生竖向荷载,还由于轮胎与路面间的滚动摩阻而产生水平切向作用力[16]。车胎与路面间的摩阻作用通常较小,水平荷载可忽略不计。但在车辆频繁启动、制动以及陡坡急弯路段,水平荷载效应趋于明显。
本节重点针对车辆制动过程中水平荷载所引起的路面动力响应进行相关数值计算,车辆启动时的情况可通过相同方法进行等效分析。为简化计算过程并体现代表性,计算中对车辆制动过程及其荷载作如下假设[8]:(1)车辆在制动过程作匀减速直线运动,车速在制动距离内迅速衰减为0;(2)车辆对路面施加竖向与水平综合荷载作用,水平及竖向荷载在荷载接触面上均呈均匀分布,且作用周期相同;(3)水平荷载仅考虑车胎与路面间的滑动摩擦作用,其荷载峰值可通过牛顿第二定律确定。
为更加全面地评价水平荷载对于路面结构剪切特性的影响,以半刚性基层路面结构为代表,采用单轴双轮组荷载,分别考虑轴重取100 kN(标准轴载)、180 kN(超载),车速取20 km/h(低速)、80 km/h(高速),对应的制动加速度取10 m/s2(紧急制动)、5 m/s2(普通制动)、2 m/s2(轻微制动)以及0 m/s2(正常行驶),以对比不同工况下的动态剪切应力。其中水平荷载峰值结合牛顿第二定律以及匀减速直线运动方程,由轴重、行车速度、加速度以及荷载作用面积确定,计算结果见表4。

表4 不同工况计算方案及结果
图13直观地反映出路面结构在车辆荷载不同制动情况下的剪切动响应状态。由表4与图13可知,在不同轴重及车速条件下,制动加速度对面层剪应力的影响均表现为:随加速度a(m/s2)的增加0(正常行驶)→2(轻微制动)→5(普通制动)→10(紧急制动),峰值剪应力基本呈线性关系增大。车速越高,相同制动加速度所引起的剪应力越大,具体而言:对于紧急制动(a=10 m/s2),车速80 km/h 时产生的剪应力较20 km/h提高了11.2%(100 kN轴载)和13.8%(180 kN轴载)。同样,轴载水平越高,相同制动加速度引起的剪应力越大,紧急制动(a=10m/s2)时,轴载180 kN产生的剪应力较100 kN增加了34.8%(20 km/h)和38.0%(80 km/h)。车速的提高与轴重的增加,都会使路面在车辆制动过程中的剪应力增大。轴载100 kN、以20 km/h车速匀速行驶的车辆荷载产生的剪应力为144.2 kPa;而轴载180 kN、车速80 km/h、制动加速度10 m/s时产生的路面剪应力为394.6 kPa。后者为前者的2.7倍,即当重载车辆在高速运行过程中面临紧急制动时,对于路面剪切受力极为不利。因此,为避免路面出现剪切类早期病害,应在控制车辆超速、超载的基础上,提高道路设计的合理性,保障车辆的制动距离,并加强频繁启动、制动路段的材料抗剪性能。
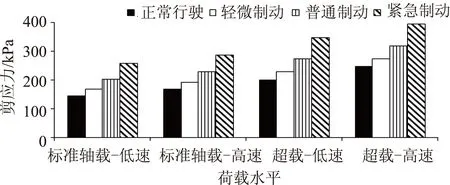
图13 不同工况的剪应力对比Fig.13 Comparison of shear stresses under different conditions
3结论
(1)沿路面深度方向,3种路面结构的剪应力最大值均出现在上面层与中面层之间(40 mm深度),即中面层顶面位置;剪应力在水平面的分布主要集中在车轮荷载作用处,其响应量随着与荷载作用点的纵、横向距离增加而急剧减小,最大值出现在轮印边缘位置处。3种路面的剪应力大小为:倒装式路面(S2)的剪应力最大,而半刚性路面(S1)与组合式路面(S3)的剪应力较为接近,S3略大于S1。
(2)相比于静态荷载,动荷载作用下的剪应力值更大,并且轴重水平越高,动、静剪应力的差异越显著。剪应力随基层模量增加而减小,随面层模量的增大而增大。剪应力随基层厚度增加逐渐减小,而随着基层厚度的增大,其递减速率呈逐渐减小的趋势,当基层厚度较大(≥40 cm)之后,通过提高基层厚度来改善路面抗剪性能的效果明显减弱。
(3)随着车速和轴重的提高,路面剪应力均逐渐增大;剪应力随轴距增加呈先增大后减小的趋势,在轴距取1.1 m时,剪应力出现最大值,而当轴距≥1.4 m 之后,剪应力响应与单轴标准轴载基本相等,且轴距变化对剪应力的影响作用较小。
(4)随着行车荷载加速度的增加,路面剪应力基本呈线性关系增大。车速越高,相同制动加速度所引起的剪应力越大;轴载水平越高,相同制动加速度引起的剪应力越大。重载车辆在高速运行过程中的紧急、频繁制动,是造成路面剪切损坏的重要原因。
References:
[1]沈金安,李福普,陈景.高速公路沥青路面早期损坏分析与防治对策 [M]. 北京:人民交通出版社,2004.
SHEN Jin-an, LI Fu-pu, CHEN Jing. Analysis and Preventive Techniques of Premature Damage of Asphalt Pavement in Expressway [M]. Beijing: China Communications Press, 2004.
[2]JTG D50—2006,公路沥青路面设计规范 [S].
JTG D40—2006,Specifications for Design of Highway Asphalt Pavement[S].
[3]聂忆华,张起森.高等级公路沥青路面剪应力分析与应用[J].中南大学学报:自然科学版,2007,38(6):1232-1238.
NIE Yi-hua, ZHANG Qi-sen. Analysis and Application of Shear Stress in High-type Asphalt Pavement[J]. Journal of Central South University: Science and Technology Editon, 2007, 38(6): 1232-1238.
[4]聂忆华,张起森,徐阳,等.高等级公路沥青路面剪应力分布研究[J].重庆建筑大学学报,2007,29(5):85-90.
NIE Yi-hua, ZHANG Qi-sen, XU Yang, et al. Distribution Regularities and Influencing Factors of Shear Stress in High Grade Asphalt Pavement Layers[J]. Journal of Chongqing Jianzhu University, 2007, 29(5): 85-90.
[5]张静,宁晓霞,王耀军.超重车辆荷载作用下沥青混凝土路面剪应力分析[J].公路,2013,1(1):165-170.
ZHANG Jing, NING Xiao-xia, WANG Yao-jun. S Shear Stress Analysis of Asphalt Concrete Pavement Under Super-heavy Traffic[J]. Highway,2013,1(1): 165-170.
[6]陈宝,吴德军,刘崭.沥青路面结构的最大剪应力[J].长安大学学报:自然科学版,2010,30(6):20-23.
CHEN Bao, WU De-jun, LIU Zhan. Maximum Shearing Stress of Asphalt Pavement Structure [J]. Journal of Chang’an University: Natural Science Edition, 2010, 30(6): 20-23.
[7]赵延庆,周长红,陈静云. 沥青路面剪应力粘弹性响应分析[J].湖南大学学报:自然科学版,2009,36(10):19-22.
ZHAO Yan-qing, ZHOU Chang-hong, CHEN Jing-yun. Analysis of the Viscoelastic Responses of Shear Stress in Asphalt Pavements[J]. Journal of Hunan University: Natural Science Edition, 2009, 36(10): 19-22.
[8]彭卫兵,刘萌成,刘书镐.刹车荷载反复作用下沥青路面剪切动响应三维有限元分析[J].公路交通科技,2009,26(9):46-52.
PENG Wei-bing, LIU Meng-cheng, LIU Shu-hao. Analysis of Shear Dynamic Response of Asphalt Pavement under Repeated Brake Loads by 3D Finite Element Method [J]. Journal of Highway and Transportation Research and Development, 2009, 26(9): 46-52.
[9]胡小弟,孙立军.非均布轮载下沥青路面计算参数变化应力分析[J].同济大学学报:自然科学版,2002,30(12):1472-1477.
HU Xiao-di, SUN Li-jun. Stress Analysis of Asphalt Pavement Caused by Changes of Mechanics Calculation Parameters under Non-uniform Distributed Tire Pressure[J]. Journal of Tongji University:Natural Science Edition,2002,30 (12): 1472-1477.
[10]黄兵,吴玉,艾长发,等.结构参数对沥青路面动态响应的影响[J].公路交通科技,2013,30(9):8-12,26.
HUANG Bing, WU Yu, AI Chang-fa, et al. Influence of Structural Parameters on Dynamic Response of Asphalt Pavement [J].Journal of Highway and Transportation Research and Development, 2013, 30(9): 8-12,26.
[11]HUANG Y H. Pavement Analysis and Design [M]. 2nd ed. Upper Saddle River: Prentice Hall, 2004.
[12]姚祖康.沥青路面结构设计[M].北京:人民交通出版社,2011.
YAO Zu-kang. Structural Design of Asphalt Pavement [M]. Beijing: China Communications Press, 2011.
[13]艾长发,邱延峻,毛成,等.考虑层间状态的沥青路面温度与荷载藕合行为分析[J].土木工程学报,2007,40(12):99-104.
AI Chang-fa, QIU Yan-jun, MAO Cheng, et al. Simulation of the Temperature and Load Coupling Effect on Asphalt Pavement Considering Inter-layer Conditions [J]. China Civil Engineering Journal, 2007, 40(12): 99-104.
[14]刘丽.沥青路面层间处治技术研究[D].西安:长安大学,2008.
LIU Li. Study on Asphalt Pavement Interlayer Treatment Technology [D]. Xi’an: Chang’an University, 2008.
[15]WU C P, SHEN P A. Dynamic Analysis of Concrete Pavements Subjected to Moving Laod [J]. Tran Engineering, 1996, 22(5):367-373.
[16]谢水友,郑传超.水平荷载对沥青路面结构的影响[J].长安大学学报:自然科学版,2004,24(2):14-17.
XIE Shui-you, ZHENG Chuan-chao. Influence of Horizontal Loads on Asphalt Pavement Structure [J]. Journal of Chang’an University: Natural Science Edition, 2004, 24(2): 14-17.
收稿日期:2015-06-18
基金项目:国家自然科学基金项目(51378438);四川省交通厅科技项目(2010B28-2);四川省教育厅科研项目(16ZB0513);中央高校基本科研业务费专项项目(SWJTU12ZT05)
作者简介:肖川(1984-),男,湖南湘潭人,博士.(xcaaa6666@sina.com)
doi:10.3969/j.issn.1002-0268.2016.07.004
中图分类号:U416.217
文献标识码:A
文章编号:1002-0268(2016)07-0019-08
Analysis on Shear Stress Property of Typical Asphalt Pavement under Dynamic Load
XIAO Chuan1,3, AI Chang-fa2,3, QIU Yan-jun2,3
(1. Sichuan College of Architectural Technology, Deyang Sichuan 618000, China;2. School of Civil Engineering, Southwest Jiaotong University, Chengdu Sichuan 610031, China;3. Sichuan Provincial Key Laboratory of Road Engineering, Southwest Jiaotong University, Chengdu Sichuan 610031, China)
Abstract:In order to investigate the response characteristics of shear stress in asphalt pavement under dynamic load, the dynamic finite element analysis models about semi-rigid pavement (S1), inverted asphalt pavement (S2), and compound pavement (S3) are established with ABAQUS. Some numerical simulations are conducted to study the spatial distribution characteristics of shear stress in the 3 kinds of typical asphalt pavement, the difference between dynamic and static shear stresses, and the influence of pavement structure and vehicle load parameters on shear stress. The result shows that (1) along the pavement depth, the maximum shear stress is at the top of mid-surface (40 mm depth); (2) the distribution of the shear stresses in the horizontal plane is mainly concentrated in the wheel load area, and the maximum value is located at the edge of wheel impression; (3) the shear stress of S2 is the maximum, and the shear stresses of S1 and S3 is close, the shear stress of S3 is slightly large than that of S1; (4) compared with the static load, the shear stress under dynamic load is larger, and the difference between dynamic and static shear stresses gradually increases with the increase of axle load level; (5) the shear stress decreases with the increase of the base modulus, while it increases with the increase of the surface modulus, and also gradually decreases with the increase of base thickness; (6) the shear stress in pavement gradually decreases with the increase of vehicle speed and axle load; (7) the shear stress increases firstly and then decreases with the increase of wheelbase, and the shear stress achieves the maximum value when the wheelbase is 1.1 m; (8) with the increase of the driving acceleration, the pavement shear stress generally increases in a linear way; (9) the shear stress of asphalt pavement increases with the increase of axle load and vehicle speed during braking.
Key words:road engineering; asphalt pavement; 3D finite element analysis; shear stress; dynamic load

