利用股市信息测度我国商业银行的利率风险

王晋忠，高　　菲

（1.西南财经大学，成都610000；2.中国银行业监督管理委员会四川监管局，成都 610042）



利用股市信息测度我国商业银行的利率风险

王晋忠1，高菲2

（1.西南财经大学，成都610000；2.中国银行业监督管理委员会四川监管局，成都 610042）

摘要：利率风险是商业银行面临的重要风险之一，可利用银行股票价格对利率变动的敏感性来对其进行量化分析。运用参数和非参数模型对我国商业银行所面临的利率风险的实证分析表明：我国商业银行存在显著的利率风险，长期利率变动对商业银行股票收益率有正向影响，而短期利率变动有负向影响；我国商业银行还面临着显著的非线性利率风险，但传统的线性利率风险更为显著；我国商业银行对长期利率变动还有显著的大小非对称性，趋势非对称性并不显著。非参数模型的估计结果表明，利率变动对银行组合收益率的边际效应不是恒定的，具有时变性特征。

关键词：股市信息；商业银行；利率风险

一、引言

随着我国利率市场化改革的深入，利率风险成为商业银行面临的重要风险之一。如何准确测量商业银行的利率敏感性是有效管理商业银行利率风险的关键。由于我国资本市场结构不够完善，利率市场化改革仍未完成，商业银行的利率风险管理意识还较弱。目前国内商业银行主要通过久期缺口、利率敏感性缺口和VaR模型三种方法对其所面临的利率风险进行衡量。但这三种方法均是单期分析方法，所利用的信息较少，利率风险衡量的效果不够理想，所以有必要对其进行改进。

股票价格是市场对于企业未来价值的预期，其中对风险的评估，以及利率变动对商业银行价值的影响，也会通过其市场价格的变动反映出来。所以，我们可以通过衡量股票收益率对市场利率变动的敏感性来测度商业银行所面临的利率风险。相对于前述的三种方法，该方法能够充分利用商业银行股票的市场信息，对利率风险的测度更加敏感，且更为全面及时。更重要是，前述三种方法主要使用的是商业银行的历史财务信息，不具有预测价值，而利用股市信息测度的商业银行利率风险更为全面及时，而且具有很好的预测性，对未来利率风险评估具有较大的参考价值。

国外相关研究文献中衡量利率风险最常用的方法是，通过使用一个简单的线性回归模型估计由银行股票收益率表示的商业银行对利率变动的敏感性。然而，利率和商业银行市场价格之间的关系可能是非线性的，造成非线性利率风险存在的主要原因有以下两个：第一，由于利率变动通过贴现因子和利率相关的收入两个方面对银行股票的价格产生影响，所以我们可以预估利率变动对股票收益率的影响不完全是线性的。第二，根据银行所使用的风险管理政策，通常侧重于运用线性工具，客观上留存下非线性利率风险。此外，银行股对利率变动的敏感性还可能取决于利率变动的趋势或震荡幅度，从而产生利率风险暴露的非对称性。尤其是，利率的上升和下降可能对银行股票价值产生不同的影响（趋势非对称）。同时，较大的利率变动相对较小的利率变动会对银行价值产生不同的影响（大小和幅度非对称）。需要注意的是，前述模型属于参数模型，都需要一个特定的函数形式，并认为它在样本时期内不会改变。非参数估计方法从一个完全不同的角度测量银行利率风险，允许估算利率变动和银行股票回报率之间的关系不遵循一个特定的函数形式。而参数模型的设定与现实经济情况更为符合，可以反映出利率风险参数时变性的特征。所以，在对商业银行的利率风险进行测量的过程中，需要对利率风险的非线性、非对称性和时变性特征进行考虑。

本文的研究目的是为我国商业银行提供一个全面的利率风险测量方法。为此，利率风险不仅使用标准的线性模型衡量，还通过非线性模型和非参数模型的估计结果来检验非线性风险是否存在。本文的主要贡献在于，首次从一个新的角度，即通过股票价格对利率变动的敏感性来量化我国商业银行所面临的利率风险，很大程度上改进了传统单一、静态的利率风险测量方法，对利率风险的测量更全面、更为敏感，能提供更多的利率风险预测价值。其次，本文不仅测量了利率变动对商业银行的线性影响，还对此前相关研究中未涉及和极易忽略的利率风险非线性特征进行了研究。最后，本文还首次尝试运用非参数模型衡量利率风险，对商业银行利率风险的时变性特征进行了分析。相对于线性模型，非参数模型具有更高的灵活性，能够更好地洞察商业银行所面临的利率风险。对商业银行利率风险的准确测量不仅对利率风险管理至关重要，同时也对其他金融领域，如资产配置、投资组合管理、资产定价以及银行监管有很大的作用。

二、文献综述

20世纪80年代初以来，大量的实证研究检验了利率风险对银行业金融机构价值的影响。大部分的研究主要基于Stone（1974）根据资产市场方法提出的两因素模型框架。[1]Stone的模型包括利率变动因素和传统的市场指数因素，用来解释银行的股票收益率。这项研究得出的主要结论有三个：首先，利率变动对银行股票收益率有显著的负向影响，普遍认为这是由于银行资产和负债的期限错配导致的（Flannery and James，1984；[2]Elyasiani and Mansur，1998；[3]Au Yong and Faff，2008；[4]Czaja et al.，2009，2010[5-6]）。第二，银行的股票回报率往往对长期利率的变化更为敏感，而不是短期利率的变化（ElyasianiandMansur，1998；[3]Bartram，2002；[7]Saporoschenko，2002；[8]Czaja et al.，2009[5]）。第三，由于使用更加先进的利率风险衡量和管理工具使得银行的股票回报率对利率的敏感度有所下降（Faff andHoward，1999；[9]BeninkandWolff，2000；[10]Ryan and Worthington，2004；[11]Joseph and Vezos，2006[12]）。Stone的研究开启了用银行股票收益率对利率变动的敏感性衡量利率风险的先河，但其研究的因素过于简单，没有考虑诸如汇率、通货膨胀率等因素对银行股票价格变动的影响。

各国学者对Stone的研究进行了扩展，其中一种扩展方式是对研究样本进行分类，对比不同行业和不同类型的股票收益率的利率风险。Lynge and Zumwalt（1980）研究了银行和工业普通股的回报率对长期和短期债券利率的敏感程度，结果表明银行普通股比工业普通股对债券的利率更为敏感，虽然工业普通股也表现出较高的利率敏感性。[13]Flannery and James（1984）认为股票的回报率由名义资产的回报率与真实的或实物资产（负债，不包括股票，可以看作是负资产）相关联的回报率两部分组成，其实证结果也验证了Stone的第一个结论。[2]Czaja，Scholz and Wilkens（2010）研究了德国各行业的利率风险报酬，实证结果表明德国大多数企业都获得了明显的正的利率风险报酬，金融机构的利率风险报酬超过非金融企业，且德国保险业利率风险的基准收益均显著高于德国银行，这似乎与传统的市场认识不符。[6]另一种扩展方式是在Stone的基础模型上加入其他的经济因素进行研究。Oertmann，Rendu and Zimmermann（2000）利用多因素模型考察了欧洲金融企业股票回报率对国内和国际利率变动的敏感程度，并运用ATP模型检验不同利率风险的回报是否相同。结果表明国内和国际利率变动均是欧洲金融企业回报率变动的动因，并且不同市场中利率变动所产生的利率风险得到的回报不同。[14]Tai（2005）和Muller and Verschoor （2006）在传统的两因素模型上加入了汇率因素，研究了美国跨国公司所面临的非对称汇率风险。[15-16]Jareno（2008）运用Stone的两因素模型与Fama和French三因素模型的延伸，研究了西班牙股市对实际利率和通货膨胀率的敏感性，结果表明，股票的回报与实际利率变动显著负相关，同时股市回报率与预期通胀率变动的相关关系并不显著。[17]

除了上述的线性模型外，还有一些实证研究探索了可能存在的比线性更复杂的利率风险暴露。Chen and Chan（1989）在这个领域做出了开创性的工作，他们研究了美国金融机构对利率周期的潜在非对称利率敏感性，结果表明，在上升和下降的利率周期中存在显著的非对称性。[18]同样的，Hallerbach（1994）的研究证明了荷兰的股票收益率对利率变动的敏感性随着时间的推移而发生变化，对利率变动趋势呈现出明显的不对称模式。他指出，特定的非线性模型能够在一定程度上解释利率上升下降之间的敏感性不对称性。[19]之后，Verma and Jackson（2008）利用多元EGARCH 模型来评估短期和长期利率与美国银行的股票组合之间存在溢出效应和不对称性。[20]他们的研究结果为货币中心银行等大型银行组合的趋势非对称性提供了证据，表明这些银行对负向利率变动比正向利率变动更敏感。

综上可知，尽管上述海外学者对不同金融市场的研究结论存在差异，但大多数研究结果表明商业银行股权收益和市场利率变化之间存在着显著的相关关系，商业银行整体所面临的利率风险可以通过上述方法测量出来，股票收益率对利率变动的敏感性是一个利率风险测量的有效方法。

三、研究方法

本文首次采用中国股市信息测度商业银行的利率风险，对我国商业银行所面临的利率风险进行全面的分析和测量，分析我国商业银行利率风险所具有的特征。因此，文章的实证研究以Stone的两因素及三因素模型为基础，测量我国商业银行利率风险的线性特征。此后，对基础模型进行扩展，测量我国商业银行利率风险的非线性和非对称性特征。最后，采用目前海外此类研究的前沿——非参数模型，分析利率风险的时变性特征。下面对论文中所采用的研究模型进行详细介绍，根据模型的形式不同分为参数模型和非参数模型。

（一）参数模型

1.线性模型

文献中提到的Stone（1974）提出的两因素线性模型是银行利率风险量化的基准模型，该模型的形式如下：

Rit表示资产i在第t期的收益率，Rmt表示市场组合的收益率，ΔIt表示利率的变动。[1]

由于利率的变动会影响市场的收益率，为了衡量利率变动对资产i收益率的净影响，需要做辅助回归：

由方程（1）（2）联合可得：

其中，γi=αi+aβmi，λi=δi+bβmi，参数λi反映了利率变动对银行股权价值的直接和间接影响。

此外，研究认为长期和短期利率均会对银行股票的收益率产生影响，所以利用短期和长期债券收益率指数代替ΔIt，模型成为三因素模型：

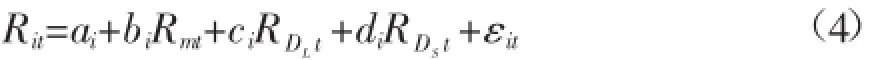
RDLt，RDSt分别表示长期和短期债券市场利率变动，由于三个因素之间存在显著的共线性，为了消除共线性，在模型估计的时候需要进行正交化处理：

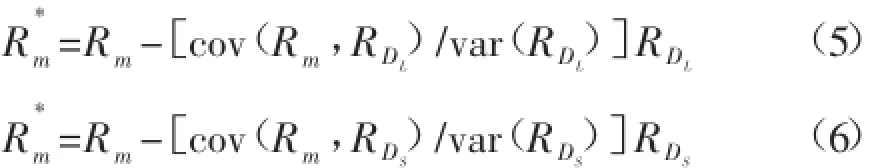
2．非线性模型

利率变动对公司股权回报率的影响可能是非线性的，所以回归方程可以写为：

f（·）表示利率变动的非线性方程，参数θi衡量了利率的非线性变动对资产i的回报率的影响。非线性形式意味着对利率的敏感度取决于利率冲击的大小。

3．趋势和大小非对称模型

检测非线性效应的另一种方法是检测银行股票回报率对利率变动的不同趋势和大小的非对称反应。一方面，银行股票回报率对利率的上升和下降变动可能有不同的反应（趋势非对称）。另一方面，大大小小的利率冲击（大小或幅度不对称），可能会对银行股票回报率有不同的影响。为了允许这些不对称性的存在，方程（1）的基本模型需要延伸。具体而言，趋势非对称性可以使用下面的模型分析：

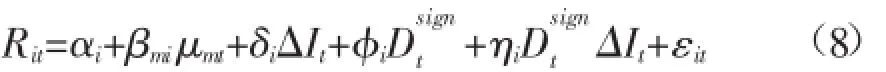
如果ΔIt＞0，虚拟变量Dsignt=1，否则为0。对于一个给定的市场组合，如果ΔIt＜0，银行股的回报率的敏感性为δi，当ΔIt＞0时，为δi+ηi。

类似的，大小和幅度非对称性可以通过以下的模型评估：

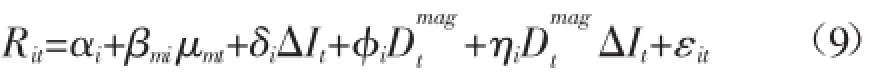
ZU和 ZL分别表示阈值的上限和下限，若ΔIt≥ZU或ΔIt≤ZL，虚拟变量Dmagt=1，否则为0。阈值可以通过ΔIt+2σΔIt和ΔIt－2σΔIt计算。若ΔIt≥ZU或ΔIt≤ZL，银行股的回报率的敏感性为δi+ηi，其余情况为δi。

这两个模型都可以用来估计与利率波动不同的趋势和大小的系数，但它们不能提供对非对称性的直接检测。为了直接检测假定，方程可以写为：

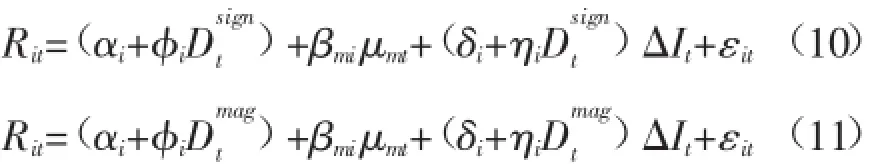
非对称性检查等价于检测ηi在统计上是否显著。

（二）非参数模型

所有的参数模型需要一个特定的函数形式，并认为它在样本时期内不会改变。非参数估计方法从一个完全不同的角度测量银行利率风险。这种方法的主要优点是它的灵活性，因为它允许估算利率变动和银行股票回报率之间的关系不遵循一个特定的函数形式。假定银行资产收益率和利率变动之间的关系由下面的通用模型给出：

未知的函数m（ΔIt）可以用在给定点ΔIj附近的泰勒展开式来近似：

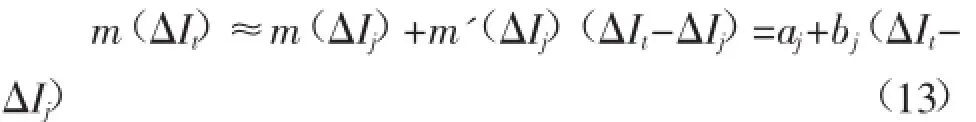
局部线性回归等价于寻找加权目标函数CV最小化的aj和bj：

Kj表示内核函数，本文采用高斯核函数，h表示内核函数的宽度参数。

Rilstone（1991）研究表明，用样本对bj进行估计是一致的和渐近正态分布，其标准差与那些由传统的参数估计的标准差是可比的。[21]因此，可以容易地对参数估计和非参数估计进行假设检验。

本文将对中国上市商业银行所面临的利率风险进行一个全面有效的测度，因此会采用上述的所有模型进行实证研究，从最基本的单因素模型分析出利率变动对商业银行影响的方向和大小，此后不断对模型进行扩展，检验利率风险的非线性、非对称性以及时变性特征。

四、实证分析

（一）样本数据的选取

本文采集2007年10月之前上市的商业银行交易数据，其样本区间为2007年10月12日至2014 年12月31日，372个时间维度的观测值。根据之前文献中的常用处理（Flannery and James，1984[2]），股票收益率采用经股息和股票分割调整后的周收益率，采用每周最后一个交易日的收盘价数据计算周回报率。①采用每周的数据而不是每天的数据是因为市场需要一段时间来了解和反应利率变动对资产价格的影响，因此，使用非常短的时间（例如日收益率）很难正确地评估企业的利率风险。此外，周数据优于月数据是因为采用周数据会获得一个更大的样本量，获得更精确的结果。对股票市场的收益我们采用沪深300指数来反映，个股及指数数据均来自CSMAR数据库。

交易所10年期固定利率国债收益率与3个月银行间固定利率国债收益率分别代表我国长期和短期利率。选择10年期政府债券的收益率来衡量银行的利率风险在已有的研究中已成为一种标准（Elyasiani and Mansur，1998[3]；Oertmann et al.，2000[14]；Faff et al.，2005[9]）。长期利率是对未来经济前景的预期，并在很大程度上决定借入资金的成本。因此，假定长期利率对企业投资决策和企业未来盈利能力的预期有更大的影响力，长期利率的数据来源于CSMAR数据库。本文用3个月银行间固定利率国债收益率表示银行的短期利率。尽管SHIBOR是我国利率市场的基准利率，但SHIBOR经常受货币发行等其他因素的影响而出现大幅波动，不能很好地反映银行所面临的真实短期利率，所以本文采用中国债券信息网发布的3个月银行间固定利率国债收益率代表短期利率。

根据Elyasiani and Mansur（1998）[3]，Faff et al.（2005）[9]，Verma and Jackson（2008）[20]and Czaja et al.（2009，2010）[5-6]的处理方法，我们将采用银行股票组合的数据，而不是单个企业的数据来检测银行的利率风险。该组合具有以下两方面的优点：它提供了一个提炼股票回报行为信息的有效方法。其次，它有助于减少个股交易数据中的噪音，从而得到更可靠的结果。按照我国商业银行分类的常用方法，我们将商业银行分为国有控股商业银行（中国工商银行、中国建设银行、交通银行、中国银行）、股份制银行（平安银行、浦发银行、华夏银行、民生银行、招商银行、兴业银行、中信银行）和城市商业银行（北京银行、南京银行、宁波银行）三类，根据之前相关研究的常用处理方法对每一类银行的股票数据进行等权重加权处理。变量的描述性统计如表1所示。

由表1可以看出各银行股票组合的收益率在均值、标准差等多方面差别较大，所以有必要将商业银行进行分组研究。所有变量的J-B统计量均显著，不符合正态分布。对变量做单位根检验，均不存在单位根，是平稳时间序列。10年期利率变动的标准差为0.0008，而短期利率变动的标准差为0.0019，是长期利率的两倍，短期利率波动更为剧烈。

由图1可以看出，平均来说长期利率高于短期利率水平。长期利率与短期利率的走势基本相同，但是短期利率的波动更大，尤其是2008年之后，我国的短期利率波动性增强，变动幅度增大。这体现出自2008年以来，我国不断推进利率市场化改革，货币市场中诸多利率已实现市场化，在市场利率的作用下，利率波动加剧，所面临的利率风险加大。

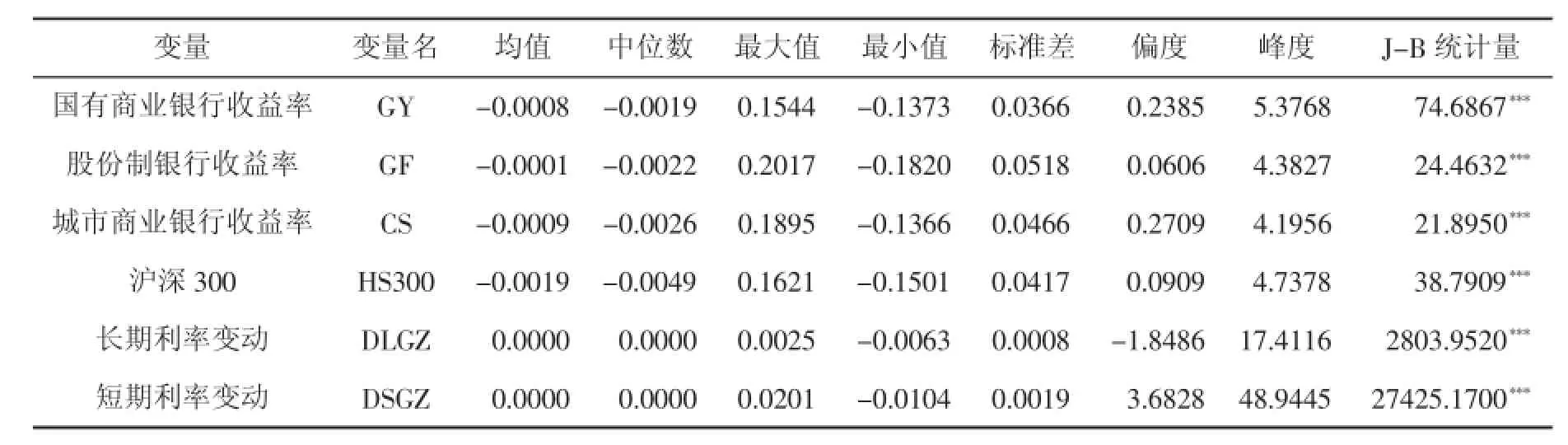
表1　变量基本统计性描述

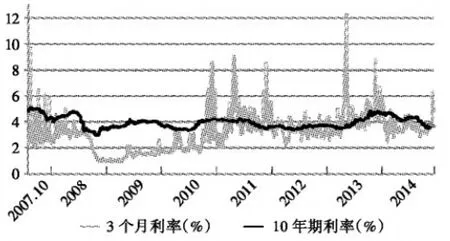
图1　样本长期利率和短期利率随时间变化情况

（二）实证结果

表2包含对三组银行组合的线性和非线性模型的系数估计。10年期国债收益率与3个月银行间固定利率国债收益率作为市场利率的代表。模型的参数均用OLS估计。非线性模型估计是利率变化采用三次函数的形式。括号中表示参数t检验的P值。HS300*表示去除利率变动因素的股指收益率。

*表示在10%的显著性水平下显著，**表示在5%的显著性水平下显著，***表示在1%的显著性水平下显著。

表3包含对三组银行组合的非对称性模型和非参数模型的系数估计。10年期国债收益率与3个月银行间固定利率国债收益率作为市场利率的代表。模型的参数均用最小二乘法估计。括号中表示参数t检验的P值。HS300*表示去除利率变动因素的股指收益率。本文的非参数估计是利用Hayfield and Racine（2008）所开发的R程序包所做的。

*表示在10%的显著性水平下显著，**表示在5%的显著性水平下显著，***表示在1%的显著性水平下显著。

由表2的实证结果可以看出：第一，在所有模型中，去除利率变动因素的股指收益率的回归结果均在1%的显著性水平下显著，表明市场因素是影响上市商业银行股票收益率的重要因素。第二，在两因素和三因素线性模型的回归结果中，长期利率均在1%的显著性水平下显著，说明长期利率对我国上市商业银行的收益率有着显著的影响。对短期利率而言，除股份制商业银行的两因素线性模型的回归系数不显著外，其他银行的短期利率的回归系数也均显著，说明短期利率也对我国商业银行的收益率有着重要影响。此外，从变量回归系数的大小可以看出，长期利率变动对商业银行收益率的正向影响系数均大于10，而短期利率变动对商业银行收益率所产生的负向影响系数均小于3，说明长期利率变动对商业银行的正向影响明显大于短期利率变动所产生的负向影响。第三，从两因素非线性模型的回归结果可以看出，长期利率的三次回归系数均在1%的显著性水平下显著。说明长期利率对我国上市商业银行的股权收益率存在显著的非线性影响。而短期利率的非线性模型回归结果则显示，短期利率对国有商业银行存在显著的非线性影响，对股份制和城市商业银行的影响却不显著。

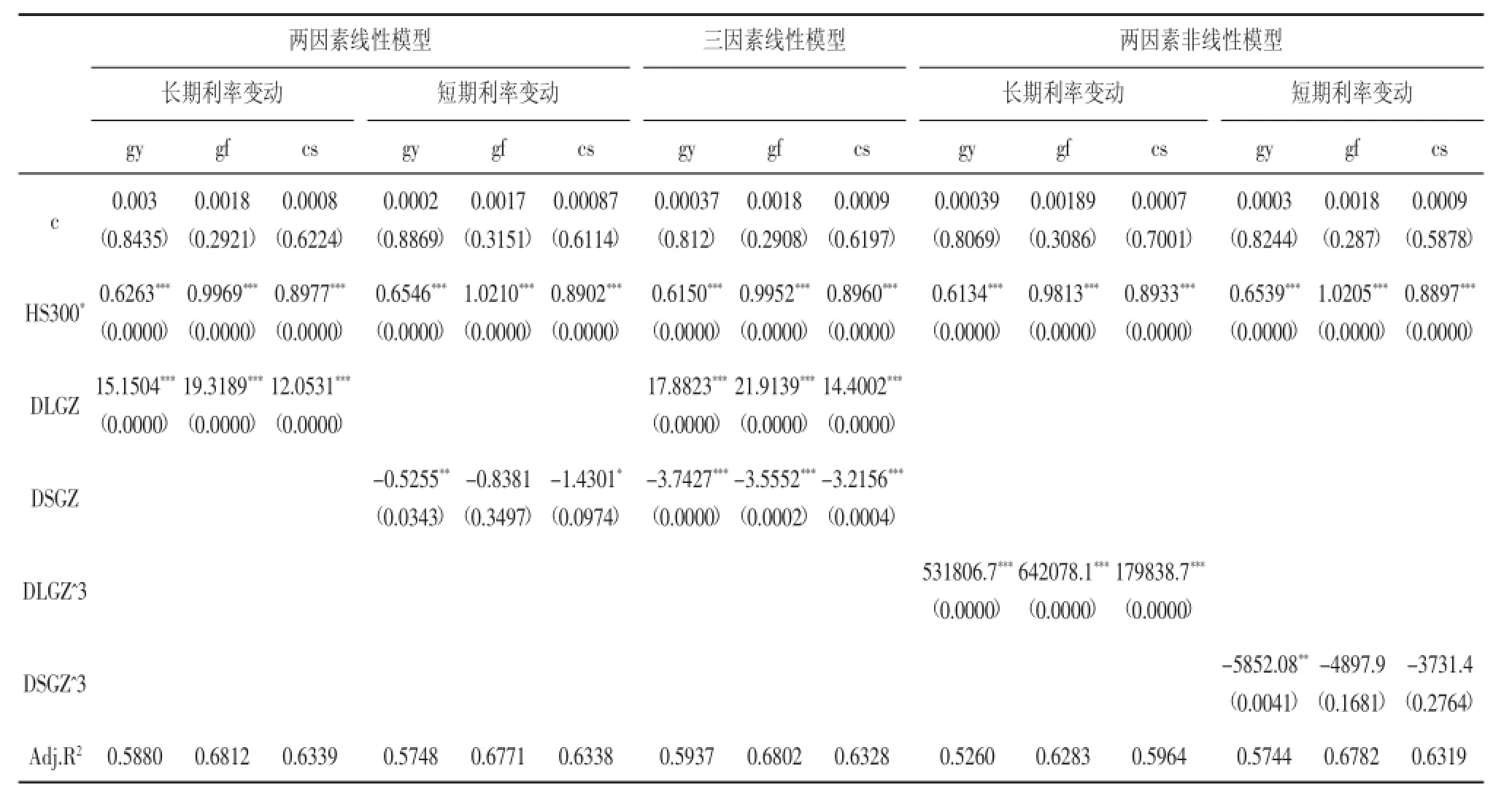
表2　　商业银行的利率风险（线性和非线性模型）

同样的，根据表3的实证结果我们可以看出：第一，趋势非对称模型的回归结果与前述线性及非线性模型的回归结果基本一致，也间接验证了表2中模型回归结果的稳健性。除了国有商业银行的短期利率趋势非对称性系数显著以外，其他银行的长短期利率的趋势非对称性系数均不显著，说明短期和长期利率变动对我国商业银行收益率影响的趋势非对称性效应不明显。第二，国有商业银行和城市商业银行的长期利率大小非对称性回归系数均在5%的显著性水平下显著，说明长期利率变动幅度大小会对国有商业银行和股份制商业银行产生显著的非对称性影响。而短期利率的大小非对称性的回归结果均不显著或显著性较低。第三，从非参数模型的回归结果可以看出，长期利率和短期利率的非参数估计系数基本显著，且回归系数的大小和符号与线性模型的回归系数基本相近，说明长期利率和短期利率确实会对我国商业银行的收益率产生显著影响。

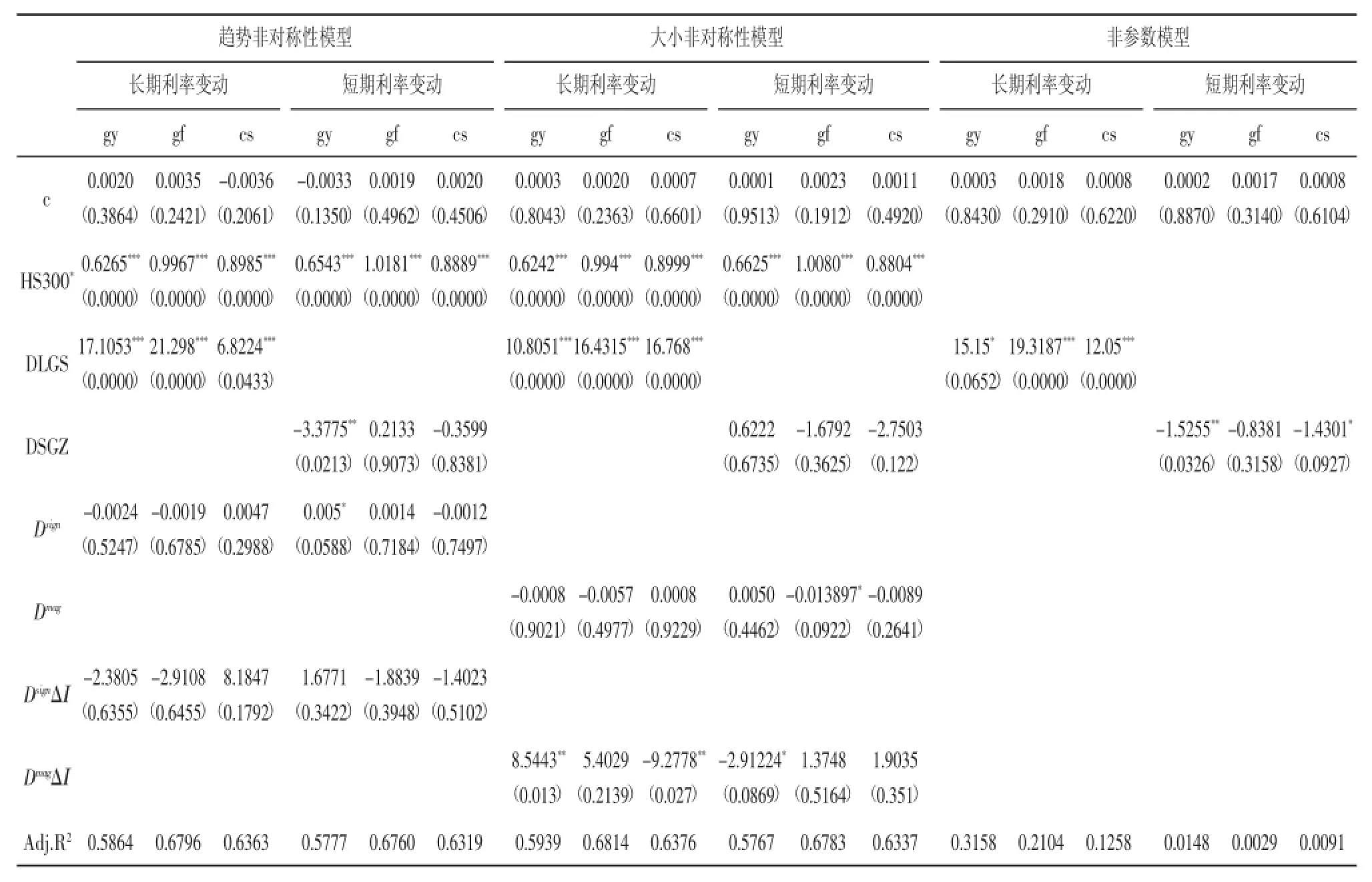
表3　　商业银行的利率风险（非对称性模型和非参数模型）

下面根据实证结果对中国上市商业银行利率风险的线性、非线性、非对称和时变性特征进行具体分析。

1.线性利率风险

长期利率的线性模型的系数为正数且显著，这意味着，长期利率上升会使我国银行股票收益率增加。这与其他国家的实证结果存在一些差异，主要是由于我国商业银行持有的长期固定收益债券相对中短期固定收益债券而言数量较少，长期利率上升会增加长期固定收益债券的当期利息收益，使银行的收益增加。同时长期利率的上升还使人们对于未来的期望回报率上升，投资的欲望增加，使股市的整体价格上涨。另一方面，短期利率的线性模型的系数为负数，意味着短期利率上涨会使银行股票的回报率下降。这主要是由于短期利率上升使银行所持有的大量中短期债券的价格下降，且这些债券即将到期，会直接影响银行当期收益，市场上的反应为股票收益率下降。由长期和短期利率变动系数的绝对值可以看出，长期利率变动的敏感性更高。此外国有控股商业银行的模型估计R2较小，反映出国有商业银行的利率风险管理能力比股份制银行和城市商业银行强，股票的收益率较少受到利率变动的影响。

2.非线性利率风险

如表2所示，三次函数在很大程度上识别了非线性的利率风险。特别是无论对长期还是短期利率，对所有的银行组合都表现出显著的非线性利率风险，说明我国商业银行除了面临线性的利率风险还面临非线性利率风险。虽然线性模型和非线性模型的自变量不同，但由R2可以看出线性模型的拟合程度均优于非线性模型，这意味着，在一般情况下，我国商业银行面临的线性利率风险更为显著。

3.利率风险的非对称性

由表3中列出的趋势和大小非对称性模型的估计结果可知，我国股份制银行对利率变动的趋势非对称性不显著，国有控股商业银行对长期和短期利率显示出显著的大小非对称性，城市商业银行对长期利率显示出显著的大小非对称性。与利率的小幅波动相比，大幅度的利率变动对我国商业银行股票收益率具有显著影响。另外非对称性模型对国有控股商业银行的解释能力更弱。同时，由表3可以看出短期利率的大小非对称并非对所有银行组合都显著，说明短期利率的异常波动对银行股票收益率的影响并不明显。

4.非参数分析

为了方便与参数模型进行比较，表3给出的非参数模型的平均估计值，作为样本逐点估计的平均值。由结果可以看出，非参数估计的平均值与线性估计在绝对值和显著性水平上都非常相似。因此，非参数方法支持长期利率变动对银行股票收益率有正向影响，短期利率变动对银行股票收益率有负向影响，同时由估计系数的绝对值可以看出，长期变化对银行股票收益率更为敏感。相较于线性估计得出的结论，逐点估计表明，利率变动对银行组合收益率的边际效应不是恒定的，并在所有的样本区间对所有的利率变动保持同样的正向或负向的影响。

五、结论

本文采用参数和非参数模型全面分析了中国上市商业银行的利率风险。通过实证分析可知，我国商业银行面临着显著的利率风险。长期利率变动对商业银行股票收益率有显著的正向影响，短期利率变动有负向影响，表明我国商业银行有显著的线性利率风险。我国商业银行还面临着显著的非线性利率风险，但传统的线性利率风险更为显著。此外，我国商业银行对长期利率变动还有显著的大小非对称性，趋势非对称性并不显著。非参数模型的估计结果表明，利率变动对银行组合收益率的边际效应不是恒定的，并在所有的样本区间对所有的利率变动保持同样的正向或负向的影响。

从本文的研究结果可以看出，长期和短期利率对我国商业银行的影响明显不同，因此在管理利率风险时需要对短期和长期利率风险用不同的工具采取针对性的管理。此外，我国商业银行除了面临传统的线性利率风险以外，其利率风险还具有非线性、非对称性和时变性特征。因此，商业银行在进行利率风险管理时，应该更多地使用金融创新产品，如可调整利率产品、资产证券化以及衍生证券，对利率风险进行管理。

参考文献：

［1］Stone B K.Systematic interest-rate risk in a two-index model of returns［J］.Journal of Financial and Quantitative Analysis，1974，9 （05）：709-721.

［2］Flannery，M.J.，James，C.M.The effect of interest rate changes on the common stock returns of financial institutions［J］.Journal of Finance，1984，39，1141-1153.

［3］Elyasiani，E.，Mansur，I.Sensitivity of the bank stock returns distribution to changes in the level and volatility of interest rate：a GARCH-M model［J］.Journal of Banking and Finance，1998，22，535-563.

［4］Au Yong，H.H.，Faff，R.Asia-Pacific banks risk exposures：pre and post the Asian financial crisis［J］.Applied Financial Economics，2008，18，431-449.

［5］Czaja，M.，Scholz，H.，Wilkens，M..Interest rate risk of German financial institutions：the impact of level.Slope，and curvature of the term structure［J］.Review of Quantitative Finance and Accounting 33，2009，1-26.

［6］Czaja，M.，Scholz，H.，Wilkens，M.Interest rate risk rewards in stock returns of financial corporations：evidence from Germany ［J］.European Financial Management，2010，16，124-154.

［7］Bartram，S.M.The interest rate exposure of nonfinancial corporations ［J］.European Finance Review，2002，6，101-125.

［8］Saporoschenko，A.The sensitivity of Japanese bank stock returns to economic factors an examination of asset/liability differences and main bank status［J］.Global Finance Journal，2002.13，253-270.

［9］Faff，R.W.，Howard，P.F.Interest rate risk of Australian financial sector companies in a period of regulatory change［J］.Pacific-Basin Finance Journal，1999，7，83-101.

［10］Benink，H.，Wolff，C.Survey data and the interest rate sensitivity of US bank stock returns［J］.Economic Notes，2000，29，201-213.

［11］Ryan，S.，Worthington，A.C.Market，interestrateandforeign exchange rate risk in Australian banking：a GARCH-M approach ［J］.International Journal of Applied Business and Economic Research，2004.2，81-103.

［12］Joseph，N.L.，Vezos，P.The sensitivity of US banks’stock returns to interest rate and exchange rate changes［J］.Managerial Finance，2006，32，182-199.

［13］Morgan J.Lynge，Jr.and J.Kenton Zumwalt.An Empirical study of the interest rate sensitivity of commercial bank returns：a muti-index approach［J］.Journal of financial and quantitative analysis.1980，Volume XV，No.3，September.

［14］Peter Oertmann，Christel Rendu and Heinz Zimmermann.Interest rate risk of European Financial Corporations［J］.European Financial Management，2000，Vol.6，No.4，459-478.

［15］Tai C S.Asymmetric currency exposure of US bank stock returns ［J］.Journal of Multinational Financial Management，2005，15 （4）：455-472.

［16］Muller A，Verschoor W F C.Foreign exchange risk exposure：survey and suggestions［J］.Journal of Multinational Financial Management，2006，16（4）：385-410.

［17］Jareno，F.Spanish stock market sensitivity to real interest and inflation rates.An extension of the Stone two-factor model with factors of the Fama and French three factor model［J］.Applied Economics，2008，40，3159-3171.

［18］Chen，C.R.，Chan，A.Interestratesensitivity，asymmetry，and the stock returns of financial institutions［J］.Financial Review，1989，24，457-473.

［19］Hallerbach，W.G.Theoretical and empirical aspects of the relation between interest rates and common stock returns［J］.In：D’Ecclesia，R.L.，Zenios，S.A.（Eds.），1994.

［20］Verma，P.，Jackson，D.Interestrateandbankstockreturns asymmetry：evidence from US banks［J］.Journal of Economics and Finance，2008，32，105-118.

［21］Rilstone，P.Nonparametric hypothesis testing with parametric rates of convergence［J］.International Economic Review，1991，32，207-227.

（责任编辑：卢艳茹；校对：李丹）

中图分类号：F832.5

文献标识码：A

文章编号：1006－3544（2016）02－0003－09

收稿日期：2016-03-22

作者简介：王晋忠，男，重庆忠县人，经济学博士，西南财经大学金融学院；高菲，女，四川南充人，中国银监会四川监管局。

The Measurement of China’s Commercial Banks’Interest Rate Risks through Stock Market Information

Wang Jinzhong1，Gao Fei2
（1.Southwest University of Finance and Economics,Chengdu 610000,China; 2.China Banking Regulatory Commission Sichuan Office,Chengdu 610042,China）

Abstract:Interest rate risk is one of the major risks facing commercial banks.Quantitative analysis of interest rate risk could be conducted by using bank stock price’s sensitivity to interest rate changes.The paper conducted empirical analysis of the interest rate risks facing China’s commercial banks by using parametric and non-parametric model.Through the analysis,it could be concluded that China’s commercial banks face remarkable interest rate risks.Long-term fluctuations in interest rates have a positive effect on commercial banks’stock returns,while short-term changes have a negative impact.Moreover,it could also be discovered that China’s commercial banks face remarkable non-linear interest rate risks,but the traditional linear risks are even more significant. Besides the abovementioned problems,China’s commercial banks’reaction to long-term interest rates fluctuations demonstrates a feature of significant asymmetry in size,but the asymmetry in trend is not significant.Lastly,non-parametric model estimation results indicate that changes in interest rates on the marginal effect of bank portfolio yield is not constant,it changes with the times.

Key words:stock market information;commercial banks;interest rate risks