基于核函数求解单调线性互补问题的新full-Newton步内点算法
吴 珊 张明望 黄正伟
(1. 三峡大学 理学院, 湖北 宜昌 443002; 2. 三峡大学 经济与管理学院, 湖北 宜昌 443002)
基于核函数求解单调线性互补问题的新full-Newton步内点算法
吴珊1张明望1黄正伟2
(1. 三峡大学 理学院, 湖北 宜昌443002; 2. 三峡大学 经济与管理学院, 湖北 宜昌443002)
摘要:本文对单调线性互补问题设计了一种基于核函数的full-Newton步内点算法.该核函数导出新的搜索方向并定义了迭代点到中心路径的邻近度量.通过应用新的技术引理,证明了该算法的多项式复杂性阶为L),这与当前求解单调线性互补问题内点算法最好的迭代复杂性阶一致.
关键词:单调线性互补问题;full-Newton步;核函数;多项式复杂性
线性互补问题是运筹学与计算数学相互交叉的一个研究领域,为线性规划、二次规划提供了一个统一的研究框架,在经济学和工程中有着广泛的应用[1].求解线性互补问题的算法很多,其中原始-对偶内点算法是一类非常重要而有效的算法[2-3].
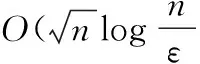
受文献[6-12]的启发,本文设计了一种基于具有线性增长项的核函数求解单调线性互补问题的新full-Newton步内点算法,并应用该核函数导出新的搜索方向且定义了迭代点到中心路径的邻近度量.同时,证明了该算法的多项式复杂性阶与当前求解线性互补问题内点算法最好的迭代复杂性阶一致.据我们所知,这是基于具有线性增长项核函数的第一个多项式full-Newton步内点算法.
文中记法:Rn表示n维欧式空间;e表示分量全为1的n维列向量;‖·‖1,‖·‖2和‖·‖∞分别表示向量的1-范数、2-范数和无穷范数;对于x=(x1,x2,…,xn)∈Rn,X表示x的对应分量构成的对角矩阵,即X=diag(x);对x,s∈Rn,xs表示对应分量乘积所得向量,即xs=(x1s1,x2s2,…,xnsn).
1算法
本文考虑如下标准形式的单调线性互补问题,即求(x,s)∈Rn×Rn(n≥2),满足
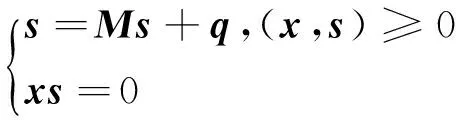
(1)
其中,q∈Rn,M∈Rn×n是半正定矩阵.
内点算法的基本思想就是用参数方程xs=μe(μ>0)取代(1)中的互补条件xs=0,得到下列方程组:

(2)
假设问题(1)是严格可行的,即满足内点条件(IPC),则对给定的μ>0,方程组(2)有唯一的解,记作(x(μ),s(μ)),并称之为问题(1)的μ-中心.所有μ-中心组成的集合{(x(μ),s(μ))|μ>0}就称为问题(1)的中心路径.当μ→0时,(x(μ),s(μ))收敛于问题(1)的最优解.
通常用Newton法求解方程组(1).对于任意给定的可行解(x,s)>0,Newton方向(Δx,Δs)满足下列方程组:
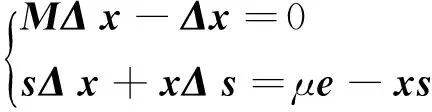
(3)
记
(4)
则方程组(3)可表示为下列尺度方程组:
(5)
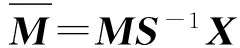
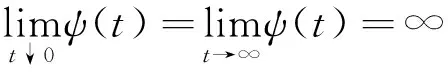
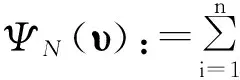
(6)
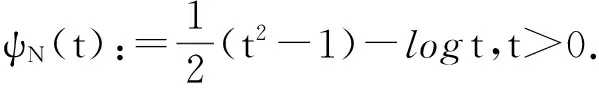
考虑如下核函数
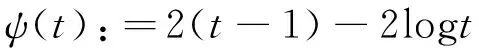
(7)
注:核函数p=0是文献[14]中核函数
在p=0时的2倍.
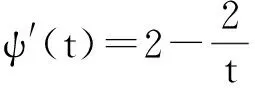
(8)
通过求解方程组(8)得到尺度搜索方向(dx,ds),再由式(4)计算得到新的搜索方向(Δx,Δs).记新的迭代点
为分析算法,引入δ(x,s;μ)来度量迭代点(x,s)到单调线性互补问题μ-中心的邻近程度,其定义如下:
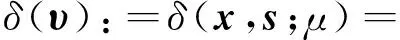
若(x,s)=(x(μ),s(μ)),则υ=e,从而δ(x,s;μ)=0;否则δ(x,s;μ)>0.
表1给出了本文算法的具体步骤.单调线性互补问题的full-Newton步内点算法:
Input
阈值0<τ<1;
精度参数ε>0;
障碍校正参数θ,0<θ<1;
严格的初始可行点(x0,s0)>0使得x0s0=μ0e,δ(x0,s0;μ0)≤τ,
begin
x:=x0;s:=s0;μ:=μ0
whilexTs>ε
求解(7)再应用(3)得到搜索方向(Δx,Δs),令
x:=x+Δx
s:=s+Δs
μ-校正:μ:=(1-θ)μ
end
end
2算法分析
本节研究full-Newton步的可行性并证明full-Newton步对于中心路径的二次收敛性,且得到该算法的多项式迭代复杂性.
2.1full-Newton步的可行性分析
由式(4)和方程组(8)的第二个方程,可得
(9)
引理2.1迭代点(x+,s+)严格可行当且仅当
证明充分性:如果x+和s+是严格可行的,由式(9)可知
必要性:令步长α∈[0,1],则定义
从而x0=x,s0=s,x1=x+,s1=s+,有x0s0=xs>0.因此,
(10)
再由式(4),可知
(11)
进一步根据式(10)和(11),有
由于(υ-e)2+e+dxds>0,则
因此
其中,(1-α)≤(1-α2)=(1-α)(1+α),所以上式中的第二个不等式成立.对α∈[0,1],由于(1-α)μ[(υ-αe)2+α(2-α)e]>0,则xαsα>0成立.因此,对α∈[0,1],xα和sα分量乘积恒大于0.又因为x0和s0是严格可行的初始点,且xα和sα关于α线性增长,所以对α∈[0,1],xα>0,sα>0.由上可知,x1和s1严格可行,则可得迭代点x+和s+严格可行.
2.2full-Newton步的二次收敛性
引理2.2[8]令δ:=δ(x,s;μ),从而可得
引理2.3令(dx,ds)是方程组(8)的唯一解,从而可知
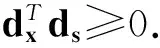

所以
证毕.
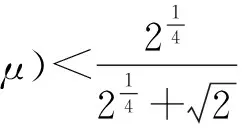
证明

证毕.
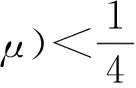
证明根据引理2.4,可知
证毕.
下面引理描述了μ-校正和full-Newton步后对邻近度量的影响.
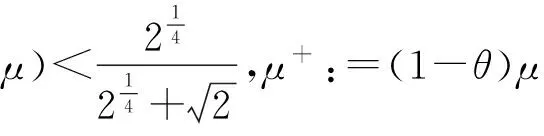

由于
min(υ2-2υ+2e+dxds)≥
则
因此,
证毕.
2.3复杂性分析
为了得到算法的多项式复杂性,需找到阈值τ和障碍校正参数θ,使得迭代开始时迭代点满足δ(x,s;μ)<τ.在full-Newton步和μ-校正后,仍有δ(x+,s+;μ+)<τ.由引理2.4可知
(12)
其中,式(12)左端关于δ单调递增.因此,
若取
(13)
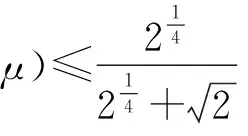
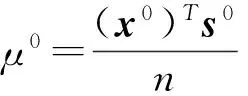
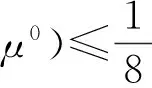
从而得到
为了使得(xk)Tsk≤ε,则
取对数,可得
(14)
再根据-log(1-θ)≥θ,则
得证.
注:由θ在式(13)的取值可知,该算法是小步校正内点算法.随着单调线性互补问题规模n的逐渐增加,不能期待在实际计算中取得太好的结果[4].今后将进一步研究大步校正内点算法及一般推广.
参考文献:
[1]韩继业,修乃华,戚厚铎.非线性互补理论与算法[M].上海:上海科学出版社,2006.
[2]雍龙泉,邓方安,陈涛.单调线性互补问题的一种内点算法[J].数学杂志,2009,29(5):681-686.
[3]KarmarkarNK.ANewPolynomial-TimeAlgorithmforLinearProgramming[J].Combinatorialoptimization, 1984, 4 (4):373-395.
[4]RoosC,TerlakyT,VialJP.TheoryandAlgorithmsforLinearOptimization:anInteriorPointApproach[M].Chichester:Wiley,1997.
[5]RoosC.AFull-NewtonStepO(n)InfeasibleInterior-pointAlgorithmforLinearOptimization[J].SIAMJournalonOptimization,2006,16(4):1110-1136.
[6]WangGQ,YuCJ,TeoKL.AFull-NewtonStepFeasibleInterior-pointAlgorithmforP*(κ)-LinearComplementarityProblems[J].JournalofGlobalOptimization,2014,59(1):81-99.
[7]PengJ,RoosC,TerlakyT.Self-regularFunctionsandNewSearchDirectionsforLinearandSemidefiniteOptimization[J].MathematicalProgramming,2002,93(1):129-171.
[8]BaiYQ,ElGhamiM,RoosC.AComparativeStudyofKernelFunctionsforPrimal-dualInterior-pointAlgorithmsinLinearOptimization[J].SIAMJournalonOptimization,2004,15(1):101-128.
[9]ZhangL,XuY.AFull-NewtonStepInterior-pointAlgorithmBasedonModifiedNewtonDirection[J].OperationsResearchLetters,2011,39(5):318-322.
[10]LesajaG,WangGQ,ZhuDT.Interior-pointMethodsforCartesianP*(κ)-LinearComplementarityProblemsOverSymmetricConesBasedontheEligibleKernelFunctions[J].OptimizationMethodsandSoftware,2012,27(4-5):827-843.
[11]LiuZ,SunW,TianF.AFull-NewtonStepInfeasibleInterior-pointAlgorithmforLinearProgrammingBasedonaKernelFunction[J].AppliedMathematicsandOptimization, 2009,60(2):237-251.
[12]KheirfamB.AFull-NewtonStepInfeasibleInterior-pointAlgorithmforLinearComplementarityProblemsBasedonaKernelFunction[J].AlgorithmicOperationsResearch,2013,7(2):103-110.
[13]KheirfamB.AFullNesterov-ToddStepInfeasibleInterior-pointAlgorithmforSymmetricOptimizationBasedonaSpecificKernelFunction[J].NumericalAlgebraControlandOptimization,2013,3(4):601-614.
[责任编辑王康平]
收稿日期:2015-11-04
基金项目:国家自然科学基金项目(71471102)
通信作者:张明望(1959-),男,教授,主要研究方向为最优化理论与应用.E-mail:zmwang@ctgu.edu.cn
DOI:10.13393/j.cnki.issn.1672-948X.2016.02.024
中图分类号:O221.2
文献标识码:A
文章编号:1672-948X(2016)02-0108-05
A Interior-point Algorithm with Full-Newton Steps for Monotone Linear Complementarity Problem Based on a Kernel Function
Wu Shan1Zhang Mingwang1Huang Zhenghai2
(1. College of Science, China Three Gorges Univ., Yichang 443002, China; 2. College of Economics & Management, China Three Gorges Univ., Yichang 443002, China)
AbstractIn this paper, a new full-Newton step interior-point algorithm is proposed based on a kernel function with linear growth term for monotone linear complementarity problem. This kernel function determines searching directions and the proximity measure between the iterates and the center path. By developing some new technical results, an iteration bound L) that coincides with the currently best known iteration bound is derived for monotone linear complementarity problem.
Keywordsmonotone linear complementarity problem;full-Newton step;kernel function;iteration bound

