基于动态补偿器的控制系统对称化

陈　磊　张国山

(天津大学 电气与自动化工程学院，天津　300072)



基于动态补偿器的控制系统对称化

陈磊张国山

(天津大学 电气与自动化工程学院，天津300072)

摘要：从一类对称方程的解出发，研究了基于动态反馈控制，即构建动态补偿器，将非对称系统转化为状态空间对称系统的问题．首先，给出存在输出反馈控制使系统状态空间对称的充分必要条件及输出反馈控制器的参数化表达式；其次，将基于动态反馈控制等效为输出反馈控制从而得到动态补偿器的参数化结果．最后，通过一个数字算例说明了所得结果的有效性．

关键词：状态空间对称；输出反馈控制；动态补偿器；稳定性

对称系统由于其特殊结构和优良的控制性能，已经得到了广泛的研究和应用．例如，文献[1-2]研究了连续时间和离散时间状态空间对称系统的H∞控制分析、输出反馈稳定性和输出反馈H∞控制分析问题．文献[3]研究了状态空间对称系统的模型降阶问题．文献[4]说明利用分散控制器的状态空间对称系统的稳定性等效于利用集中控制器的系统稳定性．文献[5]得到了计算线性时不变状态空间对称系统的计算H∞范数的显式表达式，及解决H∞范数最大化和正实性问题的静态输出反馈的显式参数化表示．文献[6]提出了一个仅和传递函数矩阵相关而不依赖有限维实现的负虚部对称系统的定义，提出了在有理情形下根据传递函数在虚轴上的行为表征负虚传递函数的充要条件．

虽然对称系统的研究已有许多结果，但是如何通过动态补偿使正常系统成为对称系统且保持稳定的研究尚未被注意到．而该项研究对于进一步研究系统的鲁棒控制及计算H∞范数均有意义．本文将研究通过输出反馈和动态补偿器使得非对称系统转化为闭环的状态空间对称系统．

1预备知识

考虑如下一个线性时不变系统(LTI)的状态空间表达式：

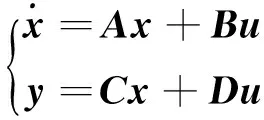
(1)

其中，x(t)∈Rn为状态向量，u(t)∈Rm为输入向量，y(t)∈Rm为输出向量，A∈Rn×n，B∈Rn×m，C∈Rm×n，D∈Rm×m均为定常矩阵．

系统(1)的传递函数矩阵表示如下

定义：系统(1)被称为状态空间对称的或内部对称的，如果满足如下条件：

(2)

如果满足G(s)=GT(s)，称系统(1)为对称的或者外部对称的．显然，由内部对称可以得到外部对称，反之则不一定正确．

为了本文需要，引入下面两个分别关于解矩阵方程AXB=D和AXB+(AXB)H=C的引理．

定义A-表示矩阵A的一个广义逆矩阵，满足AA-A=A．此时有如下引理：

引理1[7]设A∈Rm×n，B∈Rp×q，D∈Rm×q，X是n×p未知矩阵，则矩阵方程

AXB=D

有解的充分必要条件为AA-DB-B=D．其通解为X=A-DB-+Y-A-AYBB-，其中Y是任意n×p矩阵．

对于矩阵方程

(3)

其中：A∈Rm×p，B∈Rq×m和Hermite矩阵C∈Rm×m都是已知的．有如下引理：

引理2[8](a)[9]存在一个X∈Rp×q使得矩阵方程成立，当且仅当

(4)

或者，等价表示为

(5)

(b)在上述充分必要条件成立时，矩阵方程的通解可以表示成如下形式

其中，U和V是矩阵方程AUB+BHVAH=C的通解，或者可以直接写成如下形式

(6)

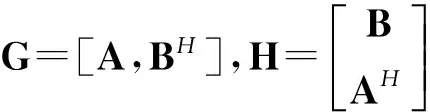
(i)AXA=A；

(ii)XAX=A；

(iii)(AX)H=AX；

(iv)(XA)H=XA．

EA和FA表示两个正交投影算子EA=Im-AA+和FA=In-A+A，其秩分别为r(EA)=m-r(A)和r(FA)=n-r(A)．

根据文献[8]中对引理2的证明，很容易得到：当矩阵C满足C=-CH时，矩阵方程AXB-(AXB)H=C的有解的充分必要条件与方程AXB+(AXB)H=C有解的充分必要条件相同；矩阵方程AXB-(AXB)H的通解表达形式为

其中，U和V是矩阵方程AUB-BHVAH=C的通解，也可以写成如下形式

(7)

其中，X0，G，H，W，W1，W2均与引理2中的定义相同．

2主要结果

2.1输出反馈情况

当系统(1)中的D=0时，在输出反馈控制

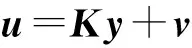
(8)

作用下，闭环系统的状态空间表达式为

(9a)

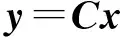
(9b)

其中，v(t)∈Rm为新的控制输入向量．

系统(9)为状态空间对称系统的充分必要条件为

A=BKC=(A+BKC)T，B=CT

基于引理1，有如下定理：

定理1假设系统(1)是一个非对称系统，且B=CT，则存在输出反馈控制(8)使得系统(9)是状态空间对称系统的充分必要条件为

此时，输出反馈增益K为

其中，Z为相应维数的任意对称矩阵．

系统(9)是稳定的，当且仅当

证明：考虑如下方程

A+BKC=(A+BKC)T

对上式进行简单变换，有

BKC-(BKC)T=AT-A

将BKC作为一个整体求解，可得

(10)

其中，Z为相应维数的任意对称矩阵．

接下来求解未知矩阵K．因为任意矩阵都可以写成一个对称矩阵和一个反对称矩阵的和的形式，即

K=KD+KF

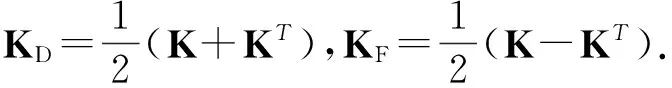
所以上式可写成

因为Z为任意对称矩阵，且B=CT，则可令

(11)

(12)

因此，矩阵方程(10)是否有解只取决于矩阵方程(11)是否有解，而与(12)无关．根据引理1，方程(11)有解的充分必要条件为

即

由于在控制系统中，B和C分别为列满秩矩阵和行满秩矩阵，根据矩阵论知识可知B-B=I，CC-=I．所以K的表达式为

系统(9)稳定的充分必要条件为A+BKC<0，即

基于引理2，有如下定理：

定理2假设系统(1)是一个非对称系统，且B=CT，则存在输出反馈控制(8)使得系统(9)是状态空间对称系统的充分必要条件为

或者，等价表示为

此时，输出反馈增益K为

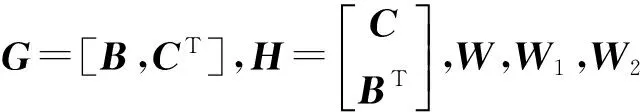
证明：对于A+BKC=(A+BKC)T变换得到

BKC-(BKC)T=AT-A

对于上式，根据引理2，且B=CT，可以很容易得到存在满足方程的K的充分必要条件和K的表达式．详细证明在此处省略．

注1：当B≠CT时，可设输出反馈控制律为u=Ky+Lv，则此时闭环系统的状态空间表达式为

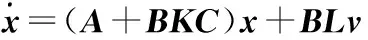
y=Cx

当BL=CT成立时，定理1和定理2依然成立．

由于B为列满秩矩阵，根据引理1，存在L使得BL=CT的充分必要条件为BB-CT=CT，此时L的表达式为L=B-CT．

2.2动态补偿情况

现在研究通过动态补偿器使闭环系统状态空间对称的情况．

为了方便起见，假设系统(1)中D=0．当D≠0时，可通过扩大系统的非动态变量的阶而消除D项[10]．假设系统(1)的动态补偿器具有如下结构：

(13a)

(13b)

(13c)

其中，xc∈Rnc是补偿器的状态；v∈Rq和vc∈Rnc分别是系统和补偿器的新的控制输入；Ac∈Rnc×nc，Bc∈Rnc×qc，Cc∈Rpc×nc，Dc∈Rpc×qc是常数矩阵．式(13c)表明可以直接得到补偿器的状态向量． 则闭环系统为

(14a)

(14b)

由文献[11]可知，系统(14)可以等价于如下系统

(15a)

(15b)

和静态输出反馈

(16)

组成． 此处

(17)

是任意变化的参数矩阵．

用一种更简洁的方式表达上述系统

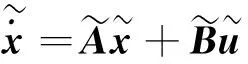
(18a)

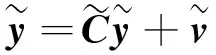
(18b)

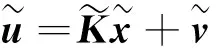
(19)

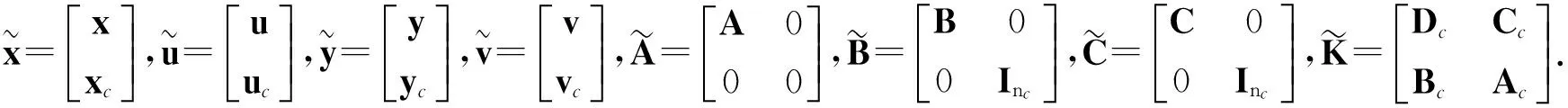
显然，根据定理1和定理2，可以很容易地得到如下定理3和定理4．

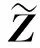
系统(14)是稳定的，当且仅当

证明：将系统(14)等价替换为系统(18)和静态输出反馈(19)，再依据定理1的证明，很容易得到存在动态补偿器(13)使得系统(14)是状态空间对称系统的充分必要条件为

即BB-(AT-A)C-C=(AT-A)．

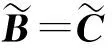
或者，等价表示为

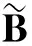
3算例

考虑系统(1)具有如下参数：

设动态补偿器(13)中的阶数nc=2，若使闭环系统为状态空间对称系统，根据定理3，可得等效的输出反馈系统参数

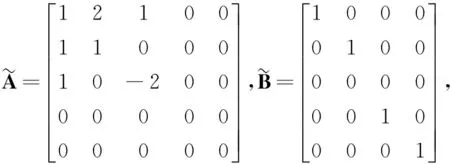
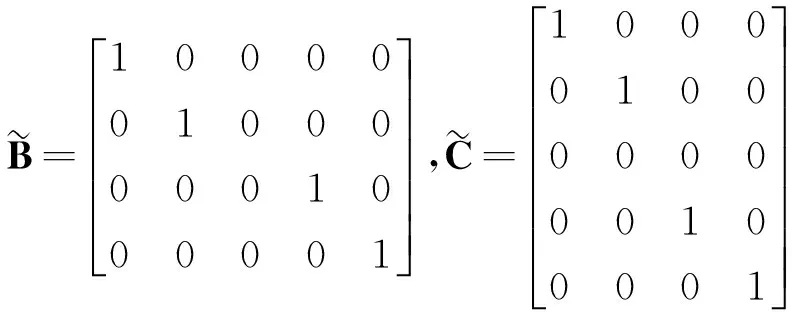
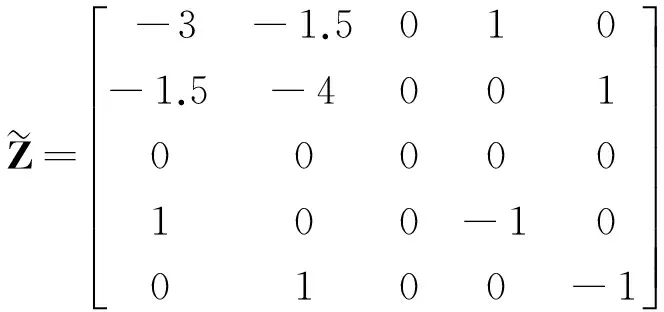
此时，

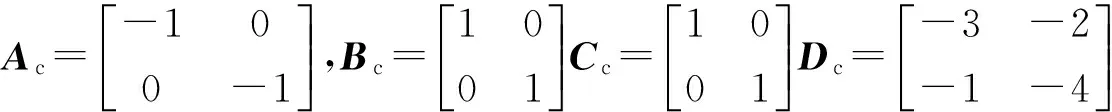
4结语

本文从一类对称方程的解出发，提出了两种基于输出反馈控制的系统对称化的方法，给出了存在输出反馈控制的充分必要条件和输出反馈控制的参数化表达式；并且通过将动态反馈控制等效为输出反馈控制，得出了基于动态补偿器的系统对称化的充分必要条件和动态补偿器的参数化结果．这些结果可以应用于实际的控制系统中和一些其他的控制问题，如H-∞控制等．

参考文献：

[1]TanK,GrigoriadisKM．StabilizationandH∞ControlofSymmetricSystems：AnExplicitSolution[J]．Systems&ControlLetters, 2001, 44(1)：57-72．

[2]TanK,GrigoriadisKM．StabilizationandH∞ControlofDiscrete-timeSymmetricSystems[J]．JournaloftheFranklinInstitute, 2007, 344(1)：58-73．

[3]Meisami-AzadM,MohammadpourJ,GrigoriadisKM．DissipativeAnalysisandControlofState-spaceSymmetricSystems[J]．Automatica, 2009, 45(6)：1574-1579．

[4]BaraGI．OntheDissipativeAnalysisandControlofState-spaceSymmetricSystems[C]//DecisionandControlandEuropeanControlConference(CDC-ECC), 2011 50thIEEEConferenceon，IEEE, 2011：459-464．

[5]FerranteA,NtogramatzidisL．SomeNewResultsintheTheoryofNegativeImaginarySystemswithSymmetricTransferMatrixFunction[J]．Automatica, 2013, 49(7)：2138-2144．

[6]KouhiY,BajcincaN,RaischJ,etal．OntheQuadraticStabilityofSwitchedLinearSystemsAssociatedwithSymmetricTransferFunctionmatricesVAutomatica, 2014, 50(11)：2872-2879．

[7]熊洪允, 曾绍标, 毛云英．应用数学基础(上册) [M]．天津：天津大学出版社, 2003．

[8]TianY,vonRosenD．SolvingtheMatrixInequality[J]．MathIneqAppl, 2012, 15：537-548．

[9]YasudaK,SkeltonRE．AssigningControllabilityandObservabilityGramiansinFeedbackControl[J]．JournalofGuidance,Control,andDynamics, 1991, 14(5)：878-885．

[10]KuijperM．DescriptorRepresentationsWithoutDirectFeedthroughTerm[J]．Automatica, 1992, 28(3)：633-637．

[11]SyrmosVL,AbdallahCT,DoratoP,etal．StaticOutputFeedback-aSurvey[J]．Automatica, 1997, 33(2)：125-137．

[责任编辑张莉]

收稿日期：2015-11-10

基金项目：国家自然科学基金(61473202)

通信作者：张国山(1961-)，男，教授，博士，博士生导师，主要研究方向为广义系统的各种控制问题等．E-mail：zhanggs@tju.edu.cn

DOI：10.13393/j.cnki.issn.1672-948X.2016.02.022

中图分类号：TP13

文献标识码：A

文章编号：1672-948X(2016)02-0097-05

Control Systems Symmetrization Based on Dynamic Compensator

Chen LeiZhang Guoshan

(School of Electrical Engineering & Automation, Tianjin Univ., Tianjin 300072, China)

AbstractProceeding from a class of symmetric equation, the problem that an asymmetric system is transformed into a state-space symmetric system through dynamic feedback control i.e. structuring dynamic compensator, is investigated. Firstly, the necessary and sufficient conditions for the existence of output feedback controllers satisfying the above condition and the parametrization of the output feedback controllers are proposed. Secondly, dynamic feedback control is equivalent to output feedback control and the parametrization of dynamic compensator are obtained. Finally, a numerical example is given to demonstrate the effectiveness of the results.

Keywordsstate-space symmetry；output feedback control；dynamic compensator；stability