基于免疫算法的墙体隔声算法实现
李运江 严凯强 范 波
(三峡大学 鄂西山地城镇建设与发展三峡大学协同创新中心, 湖北 宜昌 443002)
基于免疫算法的墙体隔声算法实现
李运江严凯强范波
(三峡大学 鄂西山地城镇建设与发展三峡大学协同创新中心, 湖北 宜昌443002)
摘要:建筑墙体在隔绝噪声中起着关键作用,由于各种建筑设备管线在墙体上开洞较多,在已知期望隔声量的条件下,如何确定墙体上缝隙最大面积成为一项重要的课题.采用免疫算法建立了隔声计算模型,将预期的隔声量定义成目标函数,单层墙的厚度、面密度与杨氏模量定义成约束变量.运用Matlab编程实现了目标函数全局最大值的求解,从而确定达到该隔声量的墙体材料、厚度和构造大样.
关键词:免疫算法;墙体;隔声量
单层均质实墙的隔声量主要与入射频率和墙体的面密度有关.此外,墙体的刚度、厚度、材料的杨氏模量以及墙体的边界条件对隔声量也有影响.墙体的隔声一般可使空动噪声降低10~60 dB.但是,一旦由于门窗产品和墙体施工质量出现漏声,会导致整个墙体的隔声量大大降[1-2].因此,墙体漏声对隔声量的影响进行反演计算研究十分必要.本文将上述3个参量确定为约束标量,在预期隔声量已知的情况下,来反向预测墙体的相关参数,诸如杨氏模量和面密度以及厚度,从而确定墙体相关材料的构造参数和厚度.
1计算模型的确定
识别多样性是免疫系统的特征之一,其数学抽象特征可以被描述为寻找多峰值函数的最优值的问题的.许多工程都存在着解决最优值的问题,这些问题可以被抽象为数学函数进行优化,特别是多峰值函数.

设待测墙体孔隙率φ,隔声量Rw,墙体面积S,则有:
声能透射系数τ为:
(1)
总透射系数为:
(2)
总墙体隔声量为:
(3)



图1 带缝隙的墙隔声计算流程图
2运算参数的确定
基于免疫算法将函数的解(抗体)进行编码,孔隙率φ与隔声量Rw为多峰函数中的两个自变量,故函数中一个抗体编码由一组(φ、Rw)组成.
2.1方案的编码
两个自变量Rw、φ分别用不同位数的二进制串来表达,自变量Rw取前6位,经计算最大值为26-1=63,其取值范围为[0,63];φ取编码后15位,通过计算得出φ的最大值为215-1=32 767,其取值为[0,32 767];最后抗体编码由两个自变量连接成21抗体编码,从而解决多峰函数最优值的问题.
抗体:X:011011110001101000110
Rwφ
2.2方案的解码

(4)
由解码公式得,φ取值为[0,1];Rw取值为[25,60].
2.3约束条件和决策变量
(5)
2.4抗体的浓度
抗体浓度:抗体本身以及与抗体相似的群体在总群体中的比例,即:
(6)
式中λ取值为0.9≤λ≤1,为一般常数.
抗体的浓度Ci及聚合适应度fitness′的关系:
(7)
式(7)中k取值为k=-0.8,为一般常数且为负值,本案程序将通过聚合适应度fitness′实现抗体群体的更新能力,同时计算抗体浓度Ci等相关值以解决多峰函数最优值问题.
3优化过程及结果
经过编程处理对(5)式中函数进行最优值运算,对其运行相关参数进行如下设置:抗体编码长度设定为20位,浓度值为0.95以及抗体终止的代数定为200代;同时考虑到抗体相似性的存在,其阈值A0为设定为0.05,抗体相互交叉的概率设定为0.6,最后产生变异的概率为0.05.计算流程如图2所示.

图2 带缝隙墙的隔声反算流程图
基于本案优化计算得出,抗体在趋于200代时呈收敛状态.同时通过计算得知,此时墙体的隔声量的期望值X1=57.2 dB,墙体缝隙面积X2=1.25×10-3m2.计算结果分布情况的由图3表示.
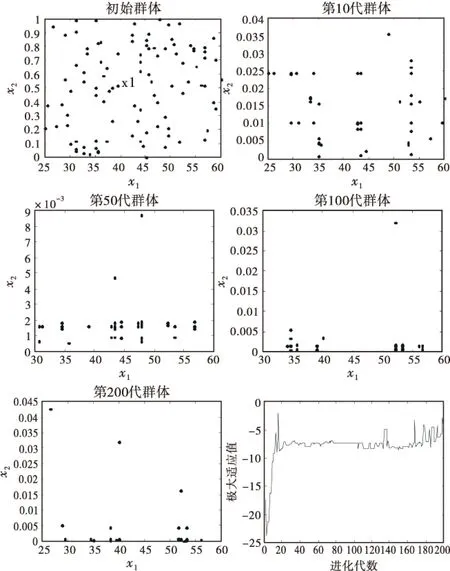
图3 进化过程及运行结果
4结语
建筑墙体在隔绝噪声中起着关键作用,其隔声设计也应得到充分重视.在已知期望隔声量的情况下,通过本文编译的免疫优化算法,可以对墙体上缝隙最大面积进行确定,这就为在施工中墙体上管道开洞的大小、插座的安装位置等方面提供了实际指导.
参考文献:
[1]华南理工大学.建筑物理[M].广州:华南理工大学出版社,2002:354-372.
[2]柳孝图,林其标,沈天行.人与物理环境[M].北京:中国建筑工业出版社,1996:139-141.
[3]黄险峰.工字型建筑构件隔声的计算[J].哈尔滨工业大学学报,2003,35(10):1253-1254.
[4]黄险峰.建筑隔声预测及隔声构件参数选择[D].广州:华南理工大学,2005.
[5]Dasgupta D. Artificial Immune Systems and Their Applications[M]. Berlin: Heidelberg Springer-Verlang,1999.
[6]王磊,潘进,焦李成.免疫规划[J].计算机学报.2000,23(8):806-812.
[7]刘克胜,曹先彬,郑浩然,等.基于免疫算法的TSP问题求解[J].计算机工程,2000,26(1):1-2.
[8]Holland J. Adaptation in Natural and Artificial Systems[M]. Cambridge, MA: University of Michigan Press, 1992.
[9]Farmer J D, Packard N H, Perelson A S. The immune System Adaptation and Machine Learning[J]. Physica, 1986, 22D, 187-204.
[10] 李运江,徐晓东.Rosenbrock函数全局最大值的免疫算法求解[J].三峡大学学报:自然科学版,2008,30(1):81-83.
[责任编辑周文凯]
收稿日期:2015-07-02
基金项目:2013年度湖北省建设科技计划项目(鄂建办[2013]195)
通信作者:李运江(1965-),男,教授,博士,硕士生导师,研究方向为建筑技术科学.E-mail:larrylee8311@163.com
DOI:10.13393/j.cnki.issn.1672-948X.2016.02.010
中图分类号:TU112
文献标识码:A
文章编号:1672-948X(2016)02-0044-03
Applying Immune Algorithm to Calculate Sound Insulation of Walls
Li YunjiangYan KaiqiangFan Bo
(Collaborative Innovation Center for Mountainous Town Construction & Development of Western Hubei Province, China Three Gorges Univ., Yichang 443002, China)
AbstractBuilding wall plays a key role in the isolated noise; as a lot of open holes in the wall for construction equipment lines; it is an important issue to determine the maximum area of wall cracks under the condition of expected sound insulation quantity. The calculation model is made by immune algorithm; the expected sound insulation quantity is defined as objective function; the areal density, thickness and Young's modulus of monolayer wall are defined as bounded variable. The global maximum of objective function is obtained by the Matlab program. Therefore, the materials, thickness of wall and construction details for sound insulation requirerment are determined.
Keywordsimmune algorithm;walls;sound insulation

