基于顶点加权的介度中心近似算法研究

王　敏　王　蕾　冯晓兵　曹宝香

1(计算机体系结构国家重点实验室(中国科学院计算技术研究所)　北京　100190)2　　　(曲阜师范大学信息科学与工程学院　山东日照　276800)



基于顶点加权的介度中心近似算法研究

王敏1,2王蕾1冯晓兵1曹宝香2

1(计算机体系结构国家重点实验室(中国科学院计算技术研究所)北京100190)2(曲阜师范大学信息科学与工程学院山东日照276800)

(wangmin01@ict.ac.cn)

摘要介度中心(betweenness centrality, BC)是衡量网络节点重要程度的一个广泛使用的指标，最快的介度中心算法需要计算n次单源最短路径，时间复杂度是O(V×E).介度中心算法的瓶颈就在于计算量太大，导致运行时间太长，无法在实际中应用，因此需要从近似算法的角度降低介度中心算法的计算量.目前介度中心近似算法在计算自然图时对计算量的降低并不显著.为了进一步降低介度中心算法的计算量，提出了一种基于顶点加权的介度中心近似算法，该算法采用顶点加权的方式将多次重复计算过程累加到一次计算过程上，结合选择高影响力源点的方法可以大大降低介度中心算法的计算量，加速比平均达到了25倍，并且最大误差百分比小于0.01%.

关键词介度中心算法；计算量；影响力；顶点加权；近似

衡量网络节点的重要程度是网络分析的一个重要方面，在衡量网络节点重要程度时，被广泛使用的一个指标是介度中心(betweenness centrality, BC)[1].介度中心算法有着广泛的使用范围，例如社区划分[2]、查找恐怖组织的领导者[3]、保护网络节点中的关键服务器、分析疾病的传播途径[4]以及分析人体关键蛋白质的组成[5]等，这些应用中的图都属于自然图.

介度中心[1]是基于最短路径计算的全局性衡量指标，在图G(V,E)中，对于任意的节点对(s,t)∈V，σs t表示节点s和t之间的最短路径条数，σs t(u)表示s，t之间的最短路径中经过节点u的条数，节点u的介度中心可以量化为

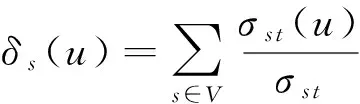
目前最快的介度中心算法是由Brandes[1]提出的，具体做法是以图中的每个节点为源点做1次最短路径计算，累加每次计算的依赖值δ，整个算法的时间复杂度是O(V×E).对于规模较大[6]的图，该方法的计算时间仍然是无法接受的，如在Intel Xeon E5645的机器，Linux 2.6.32单核的运行环境上，对于一个社交网络soc-LiveJournal1[7](4.8×106个顶点和6.8×107条边)完成1次最短路径和依赖值δs(u)计算(简称一次遍历)的时间为7 s，完成n次遍历的时间约13个月.

目前国内外有很多降低介度中心算法运行时间的研究，一类是将介度中心算法并行化缩短其计算时间；另一类是通过近似算法减少介度中心算法的计算量，从而减少计算时间.本文的工作属于第2类方法范畴.介度中心近似算法中比较有代表性的有Brandes等人[8]提出的随机近似算法，这些算法在一定程度上降低了介度中心算法的计算量.经测试发现，当选取源点数目大约为n×60%时，可以保证近似算法结果的误差是可接受的，但是对计算量只降低了约40%.在实际应用中对自然图的计算量的降低并没有使其达到实用化的程度，所以需要进一步降低介度中心算法的计算量.

本文提出了一种基于顶点加权的介度中心近似算法，该近似算法核心思想是减少计算量.通过减少相似的重复计算并结合选取高度源点的方式，使得少数次的遍历计算效果相当于多次的遍历计算效果，从而达到降低计算量的目的.实验结果显示该算法的平均加速比为25，逆序对百分比(衡量误差的1个指标，见4.2节)也都小于0.01%.该算法降低的只是单源最短路径的计算次数，所以这种方式并不会影响并行介度中心算法的并行性，与并行算法是正交的.

1相关工作

国内外对介度中心算法的工作主要集中在近似、并行、增量式计算等方面.本文的工作主要集中在近似算法的角度，目前国内外的介度中心近似算法主要分为2类：1)减少介度中心算法的整体计算量；2)减少单个顶点的介度中心值的计算量.减少介度中心算法整体计算量的近似算法主要有随机近似算法[8]、随机线性缩放近似算法[9]、随机二分近似算法等人[9].随机近似算法(Random)是由Brandes等人[10]提出的，方法是随机选择一些点作为源点进行最短路径计算.通过这种方式可以在一定程度上降低介度中心算法的计算量.随机近似算法的缺点在于随机选择源点的方式可能会选择很多低度的源点，导致离源点近的点的介度中心值偏高；其次为保证近似结果的误差可接受，在计算有向自然图时需要选取源点数目大约为n×60%，计算量仅降低了40%，算法性能提升不到1倍.

随机线性缩放算法是由Geisberger等人[9]提出的，该算法与随机近似算法源点的不同点在于通过在介度中心值计算过程中添加距离函数的方式解决了随机近似算法中有些点的介度中心值偏高的问题.随机线性缩放算法也是通过随机选择一部分源点的方式来减少计算量.该算法解决了某些介度中心值偏高的问题，提高了算法近似结果的精确度.经测试发现，在计算有向自然图时，选择与随机近似算法相同个数的源点，最重要10个点的误差与随机算法的结果相同，排名前100个点的精确度大约提高25%.在实际应用中所关注的往往是最重要的1个或者几个点，所以需要选取与随机近似算法相当的源点个数，这对计算量的降低并不明显.为了保证计算结果的误差可接受，需选取与随机近似算法相当的计算量，计算量偏大.

随机二分近似算法是由Geisberger等人[9]提出的另一种介度中心近似算法，该算法与随机线性缩放算法的不同在于距离函数的选取，根据节点距离源点的距离将距离函数定义为1个确定的值0或者1.该算法取得了与随机线性近似算法相当的精确度，但是也存在相同的问题就是对自然图的计算量降低太少，需要选取约n×60%的计算量，计算量降低较少.

另一类介度中心近似算法中比较有代表性的是由David等人[10]提出的自适应采样近似算法，该算法用来减少单个节点或者已知节点集合的介度中心值的计算量，具体做法是随机选择源点，当已知节点或者已知节点集合的介度中心值满足一定条件时停止计算.该算法的核心思想是对节点介度中心值的估算，问题在于需要提前知道哪些节点是重要的，目前还无法确定哪些点是需要关注的.

并行方面的工作主要包括介度中心算法的粗粒度并行和细粒度并行.介度中心算法的计算过程是以每个节点为根节点进行最短路径遍历和依赖值计算的过程，粗粒度并行是指并行根节点进行最短路径遍历和依赖值计算的过程，细粒度并行是指在依赖值计算或者最短路径遍历时，对遍历到同层的节点进行并行计算.

1) 在粗粒度并行方面，Jin等人[11]提出了通过并行的介度中心算法的方式来进行电网事故分析；Yang等人[12]通过并行优化介度中心算法对蛋白质网络进行了计算和分析.这些粗粒度并行的方式对小的图数据具有良好的分析效果.

2) 在细粒度并行方面，Bader等人[13]首次提出了一种基于粗粒度和细粒度同时并行的介度中心算法；Madduri等人[14]在Bader的基础上将Bader算法的细粒度并行方式中记录前驱的方法改成了记录后继的方式，进一步优化了算法的性能；Cong等人[15]通过重新布局图的节点以及图节点预取的方式对介度中心算法的细粒度并行进行了优化；Tan等人[16-18]在Bader的基础上改进了图划分方式，使得图数据逻辑地被划分在不同的处理器上，前驱节点的列表分布在每个分区上，并且在IBM Cyclops64处理器上对介度中心值计算性能进行了分析，取得了良好的性能.

3) 在异构方面，Zhi等人[19]提出了一种在GPU上的同步并行方式，图划分方式是将图中的边在线程之间进行了划分，这种并行方式也取得了较好的性能.

4) 在其他方面，Yang等人[20]提出了一种添加虚拟节点的方式来降低有权图介度中心值计算的时间，通过加虚拟节点使得图中所有边的权值相等，进而降低了有权图计算介度中心值的时间复杂度.

增量式算法的目的主要是为了计算动态变化的图的介度中心值，一方面，Lee等人[21]提出了一种基于MUC的介度中心值计算方法，该算法的核心思想是使得图的变化范围仅在MUC内部，当图数据发生变化的时候只需要计算MUC内部节点的介度中心值即可；另一方面，Miray等人[22]和Green等人[23]提出了通过记录大量中间结果的方式来计算动态变化的图，当图数据发生变化时只需要更改中间结果便可以完成对新生成图的介度中心值计算.

2基于顶点加权的介度中心近似算法

2.1研究动机

很多自然图具有无尺度特性[24]，具体特征为大多数节点只与很少的节点相连，只有极少数的点与大量的节点相连，这些极少数的节点是网络中的“枢纽”.无尺度特性表现为网络中的节点的度符合幂律分布[25]特性，如图1[24]所示，网络中1%点的边数占总边数的50%.造成自然图无尺度特征的原因是:1)网络中不断有新的节点加进来，即增长性;2)新加进来的节点总是优先连接那些度数高的点，即择优连接性.我们主要利用了自然图的择优连接性和幂律分布的特性来降低介度中心算法的计算量.

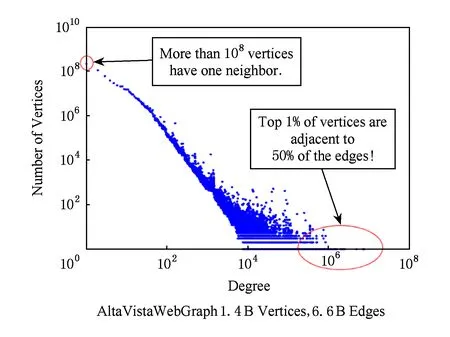
Fig. 1　Power-law degree distribution.图1　幂律分布图

为了降低介度中心算法的计算量，一方面我们利用自然图的择优连接性来减少相似的重复计算.自然图的择优连接性[24]使得新加入网络的低度节点都连接到一些高度的节点上，如图2[26]所示，以这些高度的点和其入边的点分别为源点计算最短路径时，会存在大量相似重复计算.图3是以s为源点的计算过程，图4是以s入边点为源点的计算过程.从图3和图4可以看出从n1到nk对其他点依赖值δ累加的效果和s效果是相同的，可以将这k+1次的计算通过加权的方式转变成1次的计算，累加介度中心值时只需乘以重复计算依赖值δ的次数k，具体实现为

if(u!=s)，thenBC(u)+=(1+k)×δ(u)；

if(u==s)，thenBC(s)+=k×δ(s).

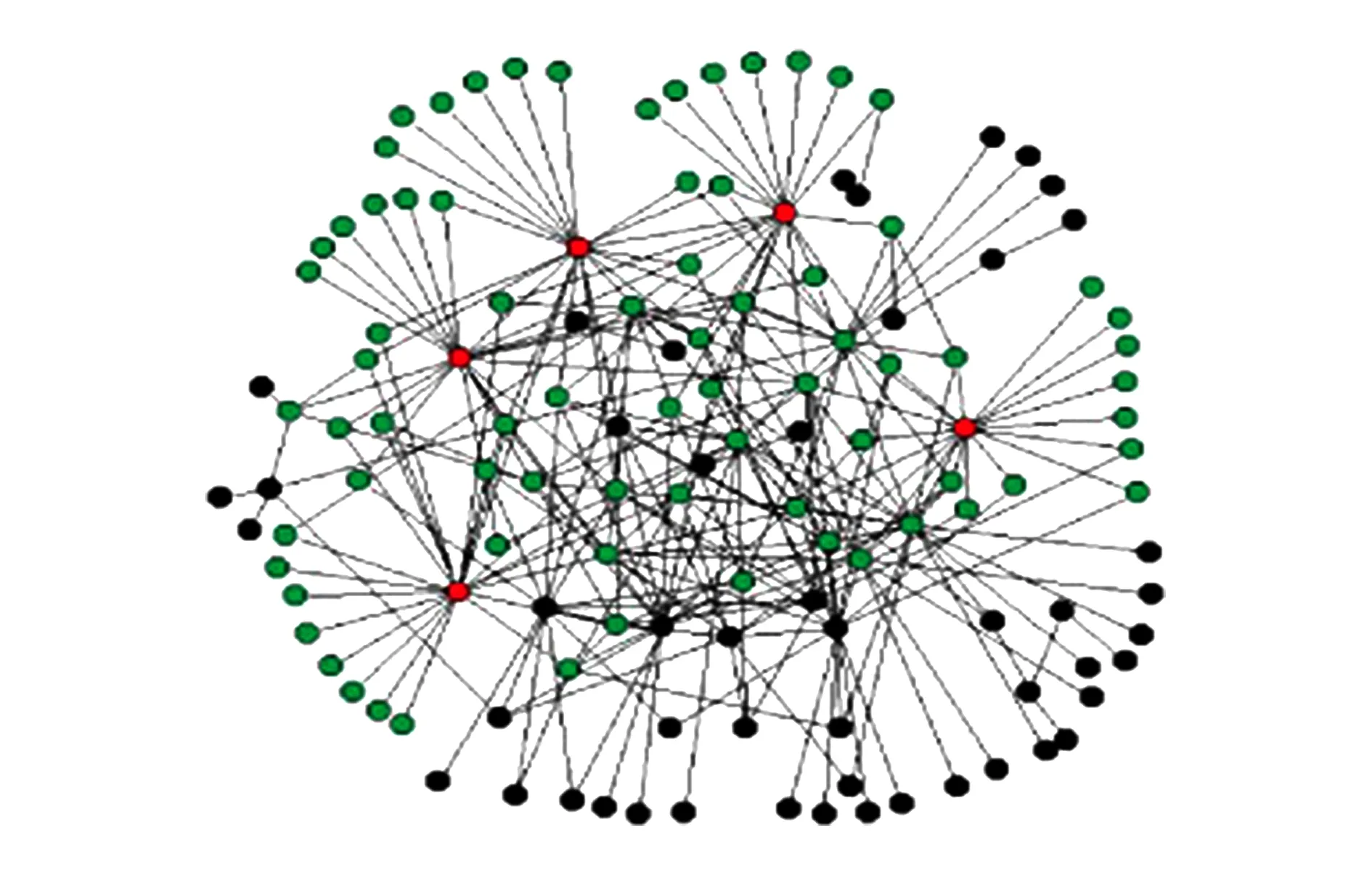
Fig. 2　Scale free network.图2　无尺度网络图

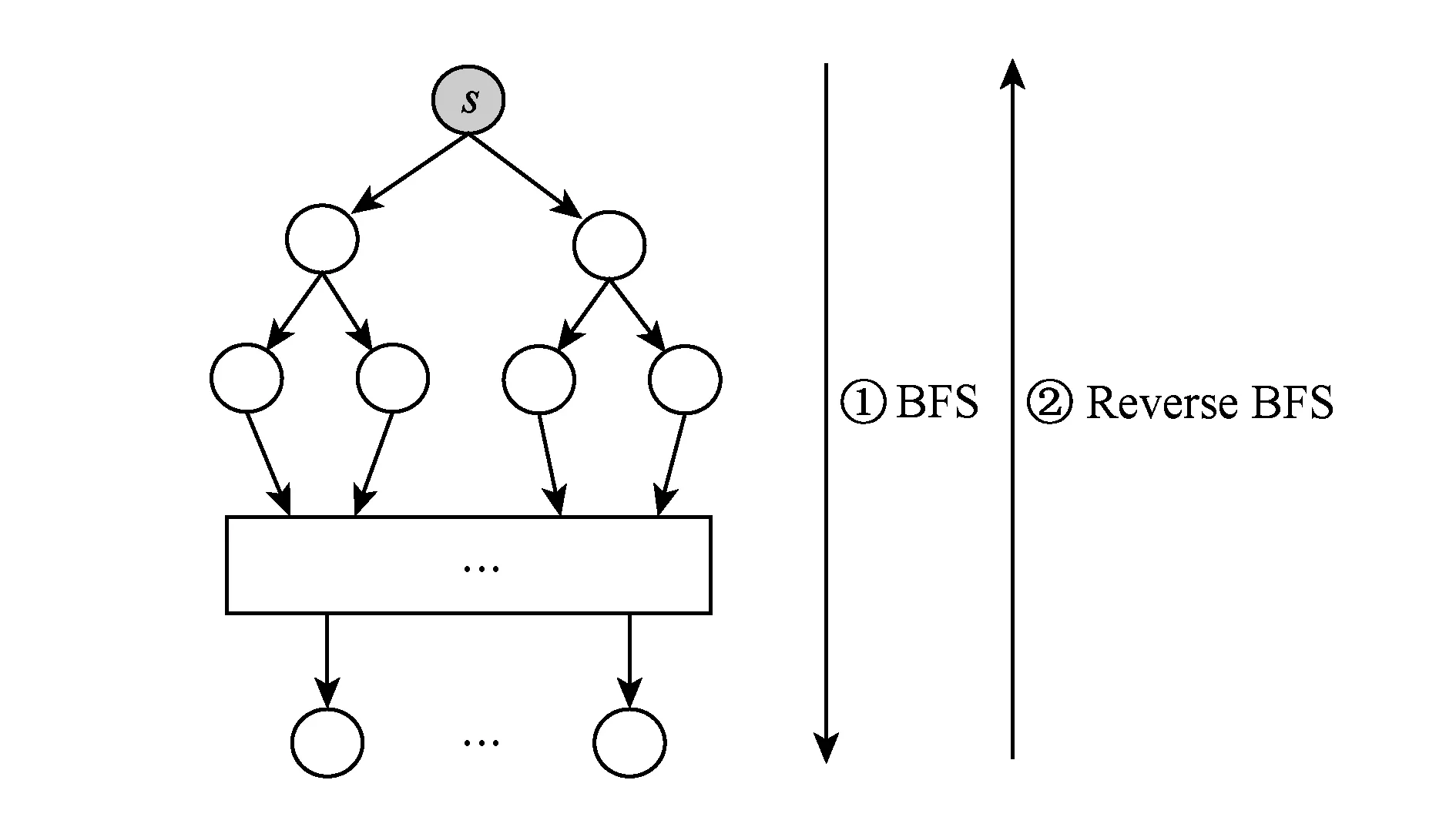
Fig. 3　The traversal of source s .图3　源点s的遍历过程

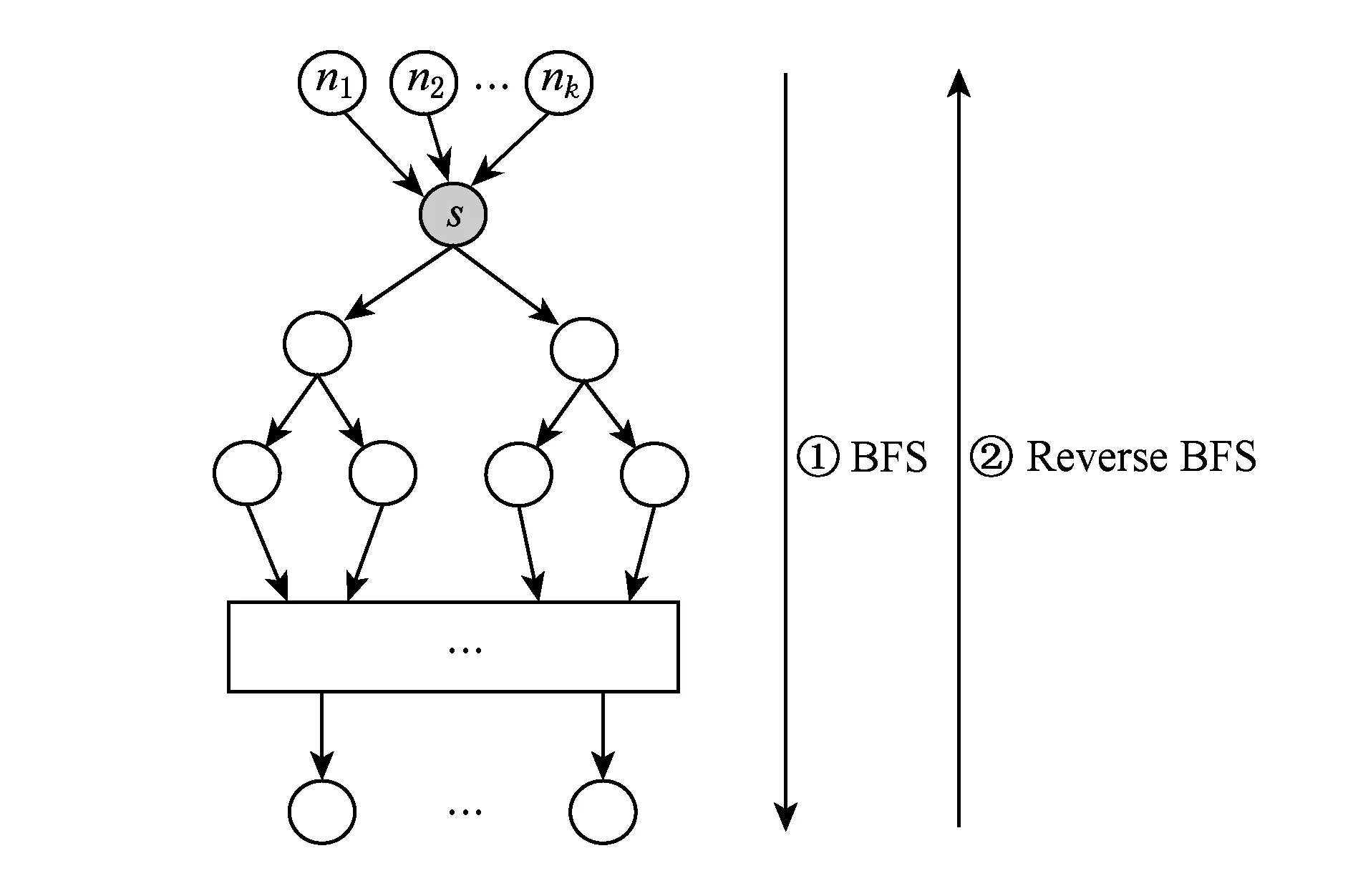
Fig. 4　The traversal of the neighbors of s.图4　s邻居的遍历过程

通过顶点加权的方式可以使得1个源点的遍历效果相当于k+1个源点的遍历效果，减少了计算量.例如使用相同源点进行介度中心计算时，选取了5种不同类型的网络图，在选择相同源点的情况下，分析了加权方式和不加权方式得出的近似结果的精确度，比较了这2种方式的结果中排名前10个点的逆序对个数(具体介绍在3.2节中，值越小结果越精确)，如表1所示，顶点加权方式的近似结果比不加权方式近似结果的逆序对数减少22倍，提高了算法精确度.

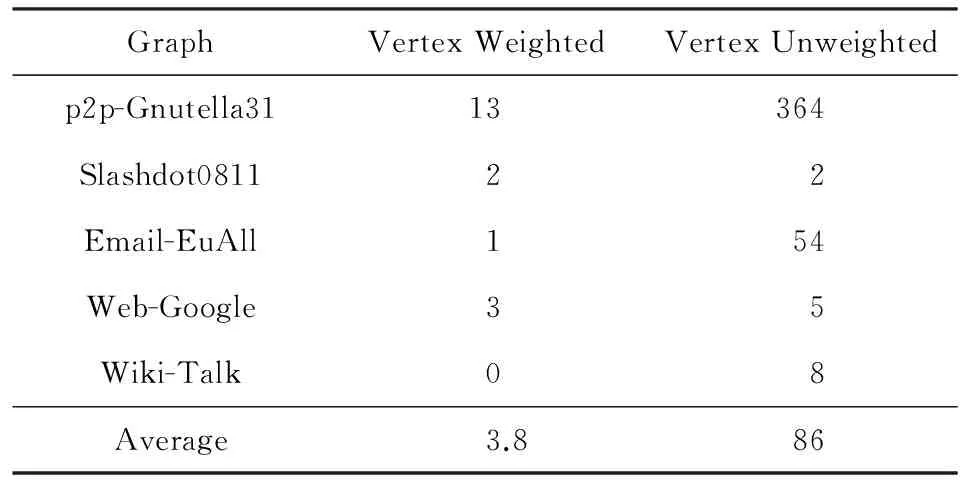
Table 1　The Number of Inversions Between Vertex Weighted

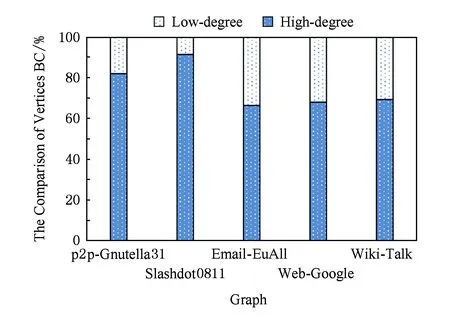
Fig. 5　The comparsion of influence between high-degree and low-degree.图5　高度点和低度点影响力对比

另一方面，利用自然图的幂律分布特性来提高介度中心算法的计算质量.自然图的幂律分布特性使得少部分的节点成为网络的“枢纽”[26]，这些高度点对其他点有着很高的影响力，在计算介度中心值时也不例外.这些高度点对介度中心值贡献较大，并且排名误差较小.例如本文选取了5个不同类型的网络图，测试其高度源点和低度源点对排名前10个点的介度中心值的贡献，如图5所示，高度点对重要点介度中心值的贡献是低度点贡献的2.15倍(柱状图的面积越大表明贡献程度越大).说明选择低度点遍历2次的效果相当于高度点遍历1次的效果，可以将计算量减少2倍多.表2是分别选高度和低度的100个源点得到的前10的逆序对数，选择高度源点的逆序对比低度源点的逆序对少了近4倍，精确度有很大提高.

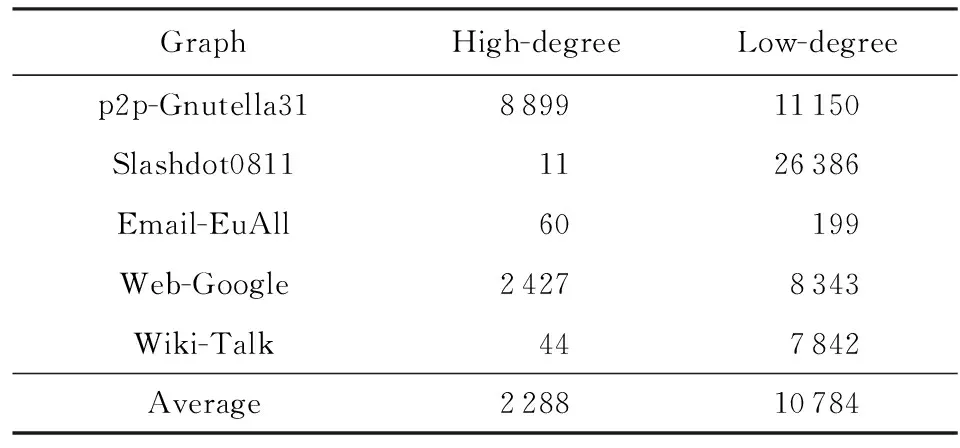
Table 2　The Number of Inversions Between High-degree Sources and Low-degree Sources

基于以上的分析和测试，我们提出了一种基于顶点加权的介度中心近似算法，该近似算法把顶点加权方法与高度源点选择方式相结合，大幅度削减计算量，从而提高计算效率.

2.2基于顶点加权的介度中心近似算法

基于顶点加权的介度中心近似算法的核心思想是：1)通过加权的方式，使得1次的遍历效果等于k+1次的遍历效果；2)选择高影响力的源点，因为高影响力源点的一次遍历效果相当于低影响力源点遍历几次的效果.这2种方式相结合选取少量的源点效果就相当于随机近似算法中选取大量源点计算的效果.顶点加权近似算法主要包含3个阶段：度数选择源点阶段、源点权值计算阶段以及介度中心值计算阶段.其中，源点选择是选择高影响力的源点(对顶点集合遍历1遍，选择度数最高的x%节点即可)；源点权值计算阶段，引入k(s)记录被选中的顶点s的重要性(顶点加权的权值)，如果顶点s某条入边点不在选中的源点集合中，则k(s)的值加1(图6(b)加括号中的行③～⑤)，这个值用于后续的介度中心值计算；在介度中心值计算阶段，根据前一步得到的被选中顶点的权值来决定需要重复累加的次数(图6(c)中的行⑤～⑧，其中行⑥之所以要加1，因为要考虑源点本身).

图6(a)是该近似算法的具体实例.在源点选择阶段，将实例中的7个点按照度(在出入度中选择较高的值，作为节点的度)的大小排序，选取度数高的n×x%的源点(x=3时已经达到了较高的精确度，如果需要更高精确度时可以增大x的值)；在源点权值计算阶段，如图6(b)所示，假设上图顶点2和顶点4被选入源点集合，顶点2，4的权值分别为3和2；在介度中心值累加阶段，如图6(c)所示，累加介度中心值时需要将重复计算的效果累加到节点的介度中心值上，即以顶点2为源点遍历时，所有点在累加介度中心值时需要依赖值乘以2的权值再累加到介度中心值上.由此可见，通过顶点加权的方式可以将经过顶点2的4次计算过程变成1次计算过程，将经过顶点4的3次计算过程变成了1次计算过程，整体计算量从7次变成了2次，计算量降低了3.5倍.

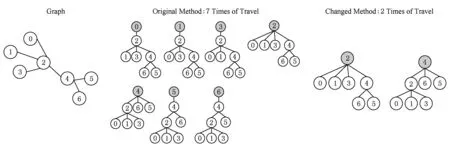
(a)Example of approximation algorithm

Thecomputingoftheweightedvaluekofsources: Input:GraphG(V,E),sources_set; Output:theweightedvaluekofsources. ①Functioncount_k() ② foreachsourcesinsource_setdo ③ foreachinsidevofsdo ④ if(visnotinsource_set)then ⑤ k[s]++; ⑥ endif ⑦ endfor ⑧ endfor ⑨returnk.ThecomputingofBC: Input:GraphG(V,E),sources_set,k Output:verticesBC ①FunctionBetweennessCentrality() ② foreachsourcesinsource_setdo ③ BFS(s); ④ delta→backward_accumulation(); ⑤ foreachvertexvinGraphGdo ⑥ ifv!=sthen ⑦ BC(v)+=(1+k[s])×delta[v]; ⑧ else ⑨ BC(s)+=k[s]×delta[s]; ⑩ endif endfor endfor returnBC.(b)Thephaseofcomputingsourcesvalueofk(c)ThephaseofcomputingBC

Fig. 6The approximation algorithm of betweenness centrality based on vertex-weighted and example.
图6基于顶点加权的介度中心近似算法及示例

3实验结果与分析

本节比较了2种近似算法(顶点加权近似算法和随机近似算法)的精确度和性能，并进行深入分析.

3.1实验方法

本文所采用的实验环境为Intel Xeon E5645的机器，Linux 2.6.32，GCC版本4.1.2，编译优化选项为-O3,2种近似算法(顶点加权近似算法和随机近似算法)和1个精确算法都是串行程序，单核执行.表3所示为我们测试数据集，都来自于真实世界.

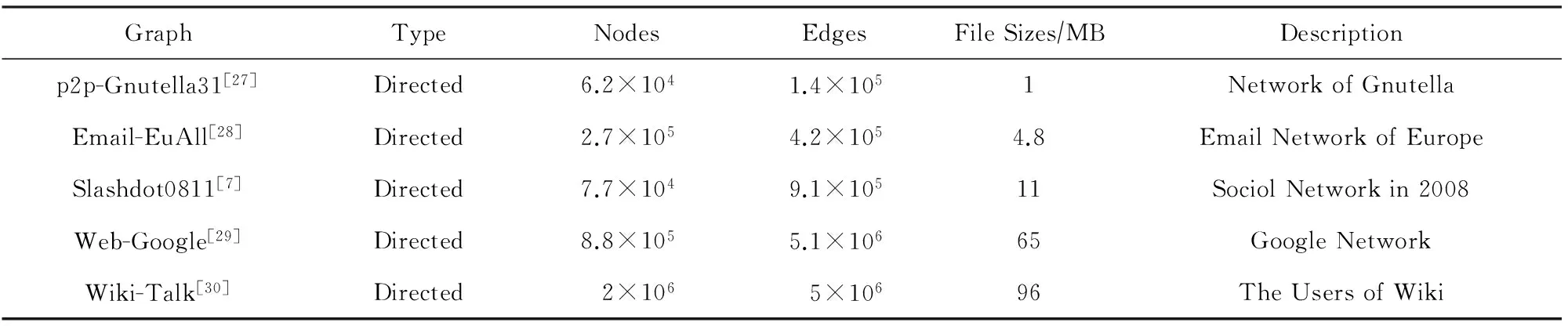
Table 3　The Figure of Test Data Sets

3.2误差评价指标

为评测近似结果的精确性本文主要采用3个评价指标，分别是topk逆序对、topk逆序对百分比、topk集合覆盖率.在实际应用中关注的只是少部分重要点的排名，所以本文所提到的误差评价指标都是从排名前k的点的角度来分析的.每个指标的介绍如下：

1) topk逆序对.一个逆序对[8]的定义为

{(u,v)|rankexact(u)>rankexact(v) and

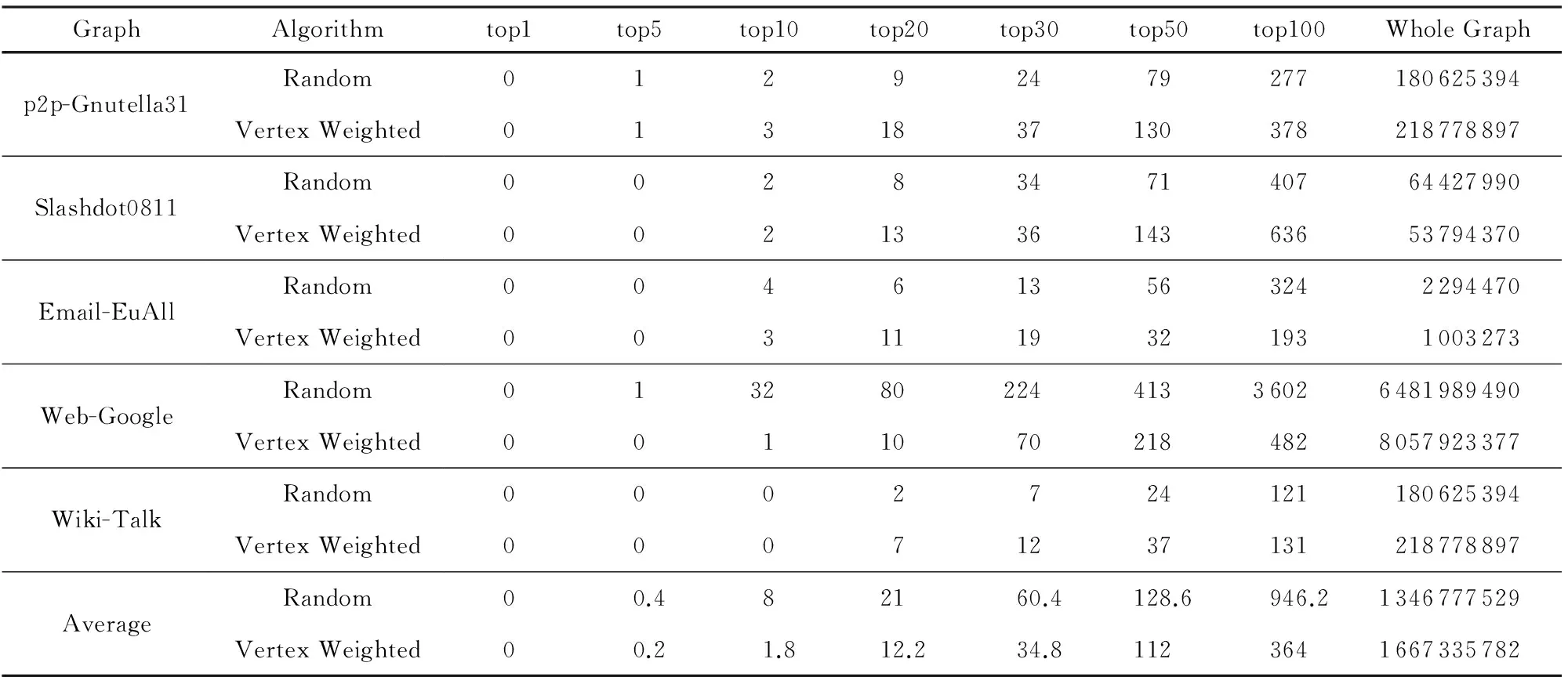
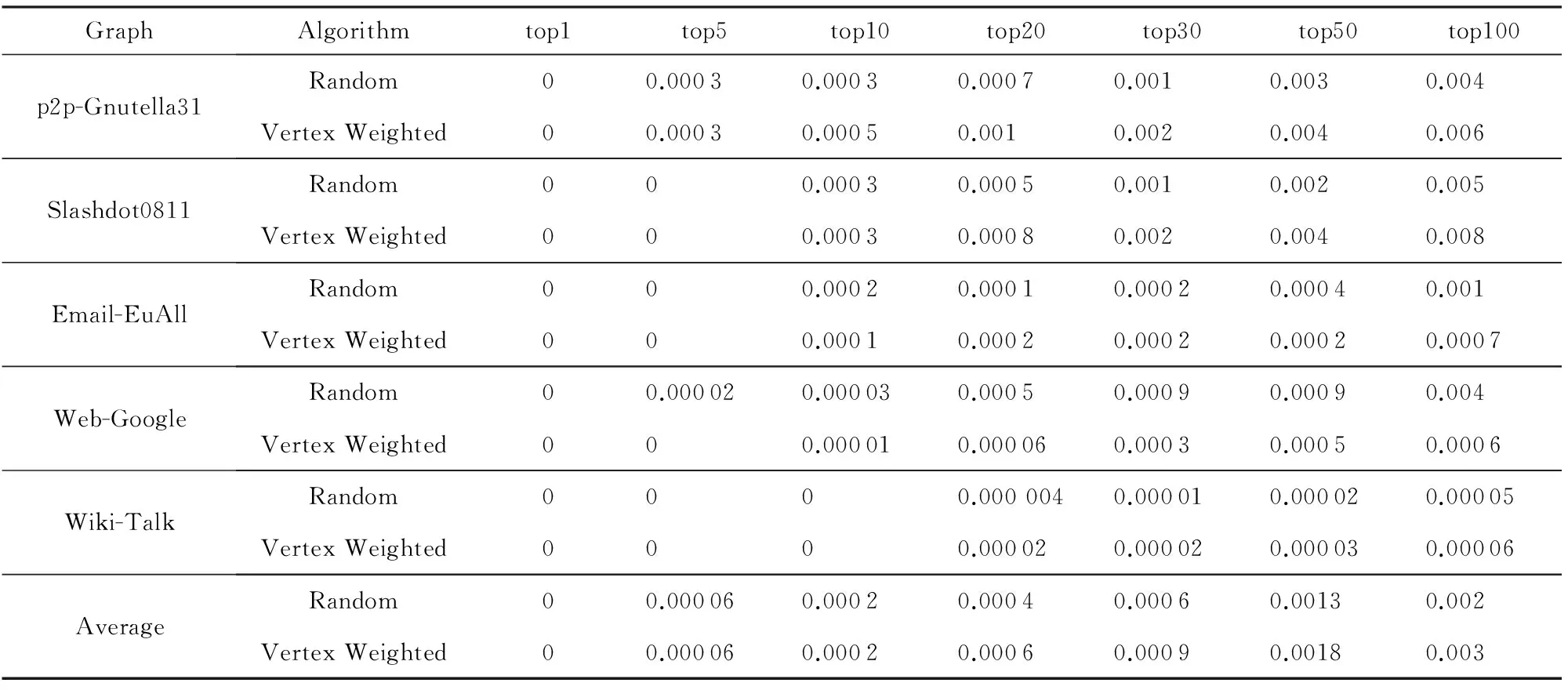
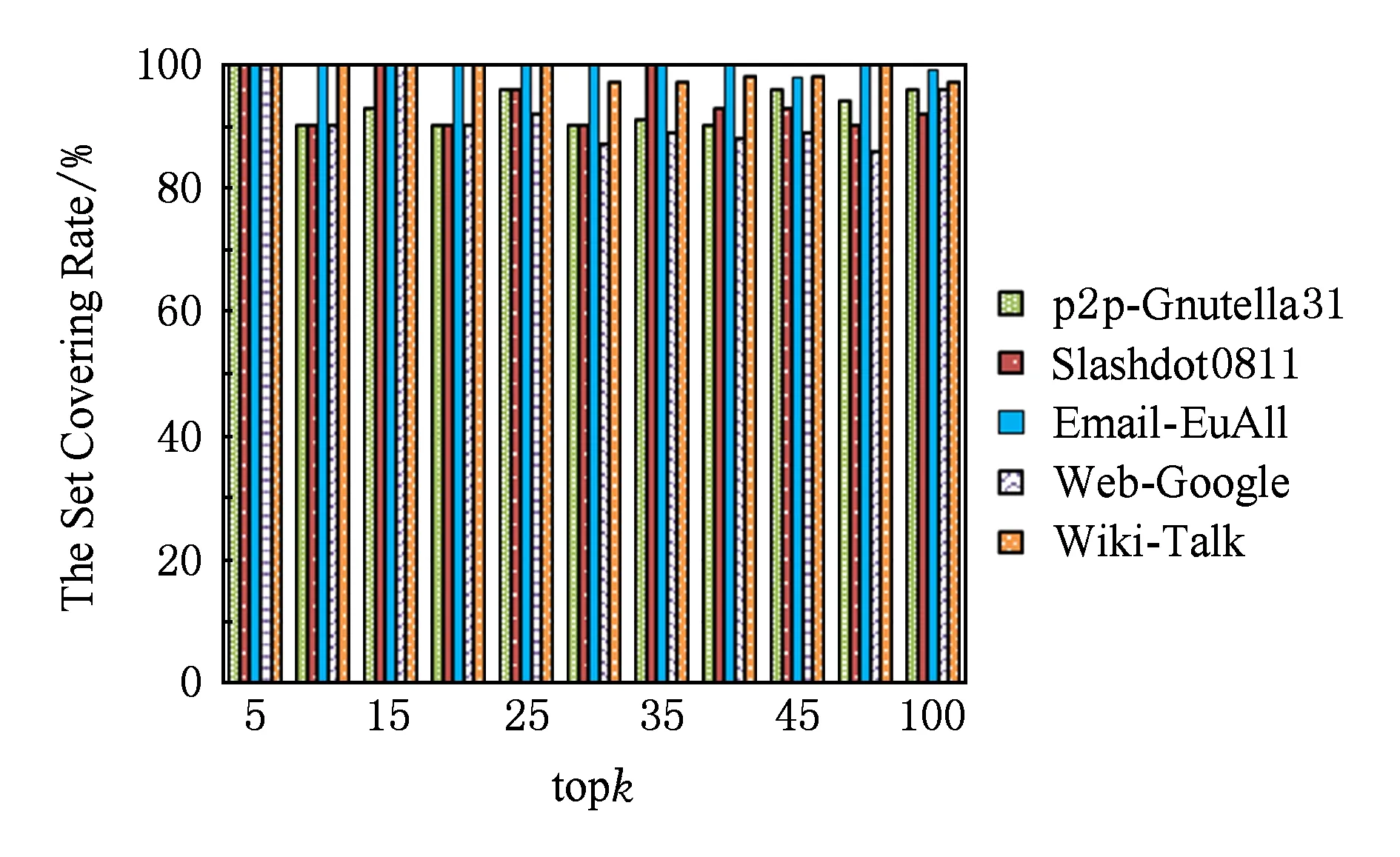
rankapprox(u)

表示近似结果排名前k个点的排名变化情况.

2) topk逆序对百分比.近似结果排名前k个点实际产生的逆序对占这k个点可能产生逆序对数的比例.

3) topk集合覆盖率.表示近似结果中排名前k个点对精确结果中排名前k个点的覆盖情况，假设近似结果前k个点中有y个点的精确结果也是前k，那么topk的集合覆盖率就可以表示为(ky)×100%.集合覆盖率可以反映出集合的精确程度.

3.3实验结果

顶点加权介度中心近似算法在保证精确度的情况下降低介度中心算法计算量，减少算法运行时间.

3.3.1误差测试结果

1) 逆序对以及逆序对百分比

表4的结果是基于顶点加权近似算法与随机近似算法(选取60%的源点)结果的逆序对数对比，顶点加权近似算法的结果中前5个点几乎是完全精确的，前10个点的平均逆序对数为1.8，随机近似算法的平均逆序对数为0.4和8.随着topk集合点数的增加，逆序对数不断增加，可以看出顶点加权算法选取少量源点的方式的精确度与随机近似算法选取60%的源点的精确度相当.表5是2种算法逆序对百分比的对比结果，从实验结果看出，虽然2种算法中随着k的增大逆序对也不断增加，但是逆序对百分比都相对较小，最高不超过0.01%，二者的精确度都是比较高的.

2) 集合覆盖率

基于顶点加权的介度中心近似算法在集合覆盖率上有很高的精确度，平均覆盖率达到95%以上.图7是通过顶点加权近似算法(大部分图约选取3%的源点)得到的近似结果的topk的集合覆盖率，topk分别取5,10,15,20,…,100，顶点加权近似算法的得到近似结果的集合覆盖率达到了平均95%以上，说明虽然集合内部存在排名变化的点，但是整个集合的精确度还是很高的.

Table 4　Random Approximation Algorithm and Vertex Weighted Approximation Algorithm for Comparing the Results of the Number of Inversions

Table 5　Random Approximation Algorithm and Vertex Weighted Approximation Algorithm for Comparing the Results of the Percentage of Inversions

Fig. 7　The set coverage of vertex weighted approximation algorithm results.图7　顶点加权算法结果的覆盖率

3.3.2性能测试结果

基于顶点加权的介度中心近似算法可以大大降低介度中心算法的运行时间，比精确算法的运行时间降低了24倍，比随机近似算法的运行时间降低了15倍.如图8和表6所示，图8是随机近似算法和顶点加权近似算法相对于介度中心算法的加速比，表示3种算法的运行时间对比，可以看出基于顶点加权的介度中心近似算法相对于介度中心算法的加速比为25，相对于随机近似算法的加速比为16，通过顶点加权结合选择高影响力源点的方式可以大大减少介度中心算法的运行时间.

Table 6　Random Approximation Algorithm and Vertex Weighted Approximation Algorithm for Comparing the Results of Performance

Notes: speedup of random is BC running timerandom running time; speedup of vertex weighted is BC running timevertex weighted running time.

Fig. 8　Approximation algorithm speedup.图8　近似算法加速比

3.3.3实验结果分析

1) 误差分析

① 逆序对与覆盖率分析

结合逆序对和覆盖率的结果可以看出，除了Wiki-Talk以外其他测试数据的近似结果top10集合中都存在逆序对，但是其集合覆盖率平均达到了95%，对测试集中精确结果中介度中心值高的前10个点的近似排名进行了研究，这5个测试集近似结果产生逆序对的原因是这些点的近似排名相对于精确排名有小范围内的变化，但近似结果也都排在了前10，所以集合覆盖率平均在98%以上，这说明顶点加权近似算法的精确度比较高.

另外，top10逆序对的产生主要是因为精确结果排名相邻的节点相互发生了变化，这些点的精确介度中心值本身相差都小于10%，说明它们的重要程度相当，排名发生了变化也是可以接受的.

② 不同类型图的精确性分析

测试集中图的误差测试结果显示，有些图的误差中top10能达到与随机近似算法相当甚至更好的精确度，有些图的精确度相对较低，按照近似结果top10的精确程度将测试集中的图分成2类：1)精确程度高的图，有Slashdot0811,Email-EuAll,Web-Google,Wiki-Talk;2)精确程度相对较低的图，如p2p-Gnutella31.

基于顶点加权的介度中心近似算法比较适合于度服从幂律分布的图，经测试可知，精确度相对高的一类图的出度和入度都服从幂律分布的特征，而精确度相对较低的一类图只有入度符合幂律分布，出度不符合幂律分布，在介度中心算法中对其他点的介度值有影响的图主要是出度，所以这类图应该主要从出度高的点进行选择，而减少重复计算量主要靠入边的多少，所以只按出度选择源点的方式会使得减少重复计算量较少，所以结果相对不是特别精确.

2) 性能分析

① 计算量对比分析

为了使近似结果的误差达到较低的误差率，在随机近似算法中选取了n×60%的源点数，基于顶点加权的介度中心近似算法选取了n×3%的源点数.本文统计显示，通过顶点加权的方式n×3%源点数的计算效果相当于不加权方式的n×40%源点数的计算效果，在结合选择高度源点的方式得到结果精确度可以达到与随机近似算法选择n×60%的源点数的结果精确度，计算量减少了约20倍，可以达到平均20多倍的加速比.

② 不同类别图的加速比分析

从不同测试数据的基于顶点加权的介度中心近似算法相对于介度中心算法的加速比结果可以看出，出入度都符合幂律分布的图的平均加速比为30，而只有入度符合幂律分布的p2p-Gnutella31加速比为3.25，这是因为p2p-Gnutella31的出度不符合幂律分布的特征，无法按照度的大小选择源点，该图进行源点选择时是按照出度选择，通过顶点加权的方式对该图的计算量降低并不明显，为了保证与随机近似算法结果的精确度相当，需要选取n×15%的源点数，是出入度都符合幂律分布图源点数的5倍左右，所以p2p-Gnutella31的加速比较低.

3.3.4与并行介度中心算法的关系分析

介度中心并行算法从粗细粒度2个方面来提高算法的并行性，粗粒度是通过并行介度中心算法的源点的图遍历和累加过程减少算法的运行时间，细粒度主要是对一次图遍历和累加过程的内部并行，例如TanGuangming等人[16]提出的无锁细粒度介度中心并行算法等.顶点加权算法只是减少了介度中心算法外层的循环次数，与介度中心的粗细力度并行是正交的，并不会影响并行算法的并行性.

4结束语

介度中心算法的瓶颈在于计算量太大，本文提出一种基于顶点加权的介度中心近似算法，该算法采用顶点加权的方式将多次的重复计算过程累加到1次计算上，结合选择高影响力源点的方法可以大大降低介度中心算法的计算量，加速比平均达到了25倍，并且最大误差百分比小于0.01%.但是这种算法只对符合幂律分布的自然图处理比较有效，因此下一步的工作就是要进一步降低其他非幂律分布图的计算量.

参考文献

[1]Brandes U. A faster algorithm for betweenness centrality[J]. Journal of Mathematical Sociology, 2001, 25(2): 163-177

[2]Girvan M, Newman M. Community structure in social and biological networks[J]. Proceedings of the National Academy of Sciences, 2002, 99(12): 7821-7826

[3]Krebs V. Mapping networks of terrorist cells[J]. Connections, 2002, 24(3): 43-52

[4]Jeong H, Mason S P, Barabesi A, et al. Lethality and centrality in protein networks[J]. Nature, 2001, 411(6833): 41-42

[5]Liljeros F, Edling C R, Amaral L A, et al. The web of human sexual contacts[J]. Nature, 2001, 411(6840): 907-908

[6]Meng Xiaofeng, Li Yong, Zhu Jianhua. Social computing in the era of big data: Opportunities and challenges[J]. Journal of Computer Research and Development, 2013, 50(12): 2483-2491 (in Chinese) (孟小峰, 李勇, 祝建华. 社会计算: 大数据时代的机遇与挑战[J]. 计算机研究与发展, 2013, 50(12): 2483-2491)

[7]Leskovec J, Huttenlocher D, Kleinberg J. Signed networks in social media[C]Proc of the 28th CHI. New York: ACM, 2010: 1361-1370

[8]Brandes U, Pich C. Centrality estimation in large networks[J]. International Journal of Bifurcation & Chaos, 2007, 17(7): 2303-2318

[9]Geisberger R, Sanders P, Schultes D. Better approximation of betweenness centrality[J]. Alenex, 2008, 11(19): 90-100

[10]Bader D, Kintali S, Madduri K, et al. Approximating betweenness centrality[G]LNCS 4863: Proc of the WAW. Berlin: Computer Science, 2007: 124-137

[11]Jin S, Huang Z, Chen Y, et al. A novel application of parallel betweenness centrality to power grid contingency analysis[C]Proc of IEEE Int Symp on Parallel & Distributed Processing. Piscataway, NJ: IEEE, 2010: 1-7

[12]Yang Q, Lonardi S. A parallel algorithm for clustering protein-protein interaction networks[C]Proc of IEEE Computational Systems Bioinformatics. Los Alamitos, CA: IEEE Computer Society, 2005: 174-177

[13]Bader D A, Madduri K. Parallel algorithms for evaluating centrality indices in real-world networks[C]Proc of the 2006 Int Conf on Parallel Processing. New York: ACM, 2006: 539-550

[14]Madduri K, Ediger D, Jiang K, et al. A faster parallel algorithm and efficient multithreaded implementations for evaluating betweenness centrality on massive datasets[C]Proc of the 23rd IEEE Int Symp on Parallel & Distributed Processing. Los Alamitos, CA: IEEE Computer Society, 2009: 537-546

[15]Cong G, Makarychev K. Optimizing large-scale graph analysis on a multi-threaded, multi-core platform[C]Proc of the 26th Int Symp on Parallel & Distributed Processing. Los Alamitos, CA: IEEE Computer Society, 2011: 414-425

[16]Tan G, Tu D, Sun N. A parallel algorithm for computing betweenness centrality[C]Proc of the 42nd Int Conf on Parallel Processing. Los Alamitos, CA: IEEE Computer Society, 2009: 340-347

[17]Tan G, Sreedhar V C, Gao G R. Analysis and performance results of computing betweenness centrality on IBM Cyclops64[J]. Journal of Supercomputing, 2011, 56(1): 1-24

[18]Tu Dengbiao, Tan Guangming, Sun Ninghui. Fine-grained parallel betweenness centrality algorithm without lock synchronization[J]. Journal of Software, 2011, 22(5): 986-995 (in Chinese)(涂登彪, 谭光明, 孙凝晖. 无锁同步的细粒度并行介度中心算法[J]. 软件学报, 2011, 22(5): 986-995)

[19]Shi Z, Zhang B. Fast network centrality analysis using GPUs[J]. BMC Bioinformatics, 2011, 12(10): 149-156

[20]Yang J, Chen Y. Fast computing betweenness centrality with virtual nodes on large sparse networks[J]. Plos One, 2011, 6(7): 1-5

[21]Lee M J, Lee J, Park J Y, et al. Qube a quick algorithm for updating betweenness centrality[C]Proc of the 21st Int Conf on World Wide Web. New York: ACM, 2012: 351-360

[22]Kas M, Wachs M, Carley K M, et al. Incremental algorithm for updating betweenness centrality in dynamically growing networks[C]Proc of Int Conf on Advances in Social Networks Analysis & Mining. Piscataway, NJ: IEEE, 2013: 33-40

[23]Green O, McColl R, Bader D A. A fast algorithm for streaming betweenness centrality[C]Proc of Int Conf on Privacy, Security, Risk & Trust. Piscataway, NJ: IEEE, 2012: 11-20

[24]Pastor-Satorras R, Vespignani A. Epidemic spreading in scalevfree networks.[J]. Physical Review Letters, 2001, 86(1): 3200-3203

[25]Tang Daquan, He Mingke, Meng Qingsong. Research on searching in unstructured P2P network based on power-law distribution and small world character[J]. Journal of Computer Research and Development, 2007, 44(9): 1566-1571 (in Chinese)(汤大权, 贺明科, 孟庆崧, 基于幂律分布和小世界特性的无结构P2P网络中搜索方法研究[J]. 计算机研究与发展, 2007, 44(9): 1566-1571)

[26]Costa L F, Rodrigues F A, Travieso G, et al. Charac-terization of complex networks: A survey of measurements[J]. Advances in Physics, 2007, 56(1): 167-242

[27]Ripeanu M, Foster I, Iamnitchi A. Mapping the gnutella network: Properties of large-scale peer-to-peer systems and implications for system design[J]. IEEE Internet Computing Journal, 2002, 6(1): 85-93

[28]Leskovec J, Kleinberg J, Faloutsos C. Graph evolution: Densification and shrinking diameters[J]. ACM Trans on Knowledge Discovery from Data, 2006, 1(1): 1-42

[29]Leskovec J, Lang K J, Mahoney A D M W. Community structure in large networks: Natural cluster sizes and the absence of large well-defined clusters[J]. Internet Mathematics, 2008, 6(1): 29-123

[30]Laura L, Donato D, Leonardi S, et al. Large scale properties of the Webgraph[J]. European Physical Journal, 2004, 38(2): 239-243

Wang Min, born in 1990. Master. Her main research interests include parallel computing and graph algorithm.

Wang Lei, born in 1976. PhD, assistant professor. Her main research interests include parallel computing and compiler optimization.

Feng Xiaobing, born in 1969. Professor and PhD supervisor. His main research interests include compiler optimization and binary translation.

Cao Baoxiang, born in 1955. Professor and master supervisor. Senior member of China Computer Federation. His main research interests include database and enterprise informationization.

收稿日期：2014-12-10；修回日期：2015-05-13

基金项目：国家“八六三”高技术研究发展计划基金项目(2015AA011505)；国家自然科学基金项目(61402445，61303053，61202055，61221062)This work was supported by the National High Technology Research and Development Program of China (863 Program) (2015AA011505) and the National Natural Science Foundation of China (61402445，61303053，61202055，61221062).

通信作者：王蕾(wlei@ict.ac.cn)

中图法分类号TP311

An Approximation Algorithm of Betweenness Centrality Based on Vertex Weighted

Wang Min1,2, Wang Lei1, Feng Xiaobing1, and Cao Baoxiang2

1(StateKeyLaboratoryofComputerArchitecture(InstituteofComputingTechnology,ChineseAcademyofSciences),Beijing100190)2(CollegeofInformationScienceandEngineering,QufuNormalUniversity,Rizhao,Shandong276800)

AbstractBetweenness centrality (BC) is a widely used indicator to measure the importance of network vertices. Currently the fastest time complexity of the algorithm is O(V×E). When computing the BC of vertices in networks, we need to do n times searches of single source shortest path. In big data era, networks have more nodes and edges, and the amount of calculation of BC algorithm is large. The huge amount of calculation makes the algorithm need a long time to compute each vertices’ BC value, and the algorithm cannot be applied in practice. The related work focuses on approximation to reduce the running time of BC algorithm, but they also can not reduce the amount of calculation of BC algorithm significantly. In order to further reduce the amount of the calculation of BC algorithm, we propose a vertex weighted approximation algorithm to reduce the amount of calculation of BC algorithm, and the algorithm can make the calculation process be repeated many times to accumulate on a calculation by vertex weighted and select high-impact vertex as source to compute BC. We can reduce the amount of calculation significantly in this way, and meet the requirement of lower error rate and high performance. The approximation algorithm of BC based on vertex weighted can achieve 25 times speedup, and the error rate is lower than percentage of 0.01.

Key wordsbetweenness centrality (BC) algorithm; calculation; influence; vertex weighted; approximation