结合互补度的基于扩展规则#SAT问题求解方法

欧阳丹彤　贾凤雨　刘思光　张立明

(吉林大学计算机科学与技术学院　长春　130012) (符号计算与知识工程教育部重点实验室(吉林大学)　长春　130012)



结合互补度的基于扩展规则#SAT问题求解方法

欧阳丹彤贾凤雨刘思光张立明

(吉林大学计算机科学与技术学院长春130012) (符号计算与知识工程教育部重点实验室(吉林大学)长春130012)

(ouyd@jlu.edu.cn)

摘要#SAT问题又称模型计数(model counting)问题是人工智能领域的研究热点之一，在人工智能领域被广泛应用.在对基于扩展规则的#SAT问题求解方法CER(counting models using extension rules)深入研究的基础上，提出一种结合互补度的#SAT问题求解方法.在计算给定子句集的模型个数时，利用SE-Tree(set enumeration tree)形式化地表达计算过程，逐步生成需要计算的子句集合，并在SE-Tree中添加终止结点，避免大部分含互补文字子句集合的生成，且不会因剪枝而导致求解不完备.提出互补度的概念，在扩展SE-Tree结点时按照互补度由大到小的顺序扩展，较早地生成含互补文字且长度较小的子句集合，有效减少枚举树生成的结点个数，进而减少对子句集合判断是否含互补文字的计算次数.实验结果表明：与CER方法相比该方法效率较好，且进一步改进了CER方法在互补因子较低时求解效率低下的不足.

关键词扩展规则；模型计数；CER方法；互补度；集合枚举树

命题可满足问题(propositional satisfiability problem, SAT)是人工智能领域中关键研究问题，有着相当广泛的应用，如在智能规划领域将规划问题编译成SAT问题进行求解[1]，同样地其还被应用于求解基于模型的诊断问题[2]以及模型检测问题中[3].迄今为止，国内外学者已对求解SAT问题的方法做了许多研究和改进[4-7].对SAT问题的求解算法主要分为基于DP(Davis-Putnam)[8]的完备性算法和基于局部搜索的非完备性算法.完备性算法虽然可以准确判定任意命题公式的可满足性，但随着问题规模的增大，求解时间也会随之以指数级增加，其不适合于大规模的SAT问题求解.基于局部搜索的非完备性算法虽然不能判定命题公式不可满足，但在可满足的SAT问题中可以快速地得到一个解，对于大规模问题也有较好效率，因此近年来获得了许多研究人员的关注.但对于局部搜索算法都面临着一个共同的问题，即陷入局部最优.格局检测策略(configuration checking)[9-10]可以有效地解决局部最优问题，并且广泛应用于局部搜索算法中.

实际上，大部分计算复杂性是NP完全的问题，都可以在多项式时间内转化成SAT问题来求解，然而在人工智能领域存在着许多复杂性高于NP完全的问题，例如贝叶斯推理、概率规划等问题[11-13]在转换成命题公式后，只判断是否可满足是不够的，还需要计算命题公式模型(可满足赋值)的个数.#SAT问题即是这样的一类问题.它是SAT问题的重要扩展，需要计算出给定命题公式所有模型的个数，计算复杂性是#P完全的[14-15].如何高效求解#SAT问题对人工智能的很多领域都有深远意义.

#SAT问题一直备受广大研究人员的关注.1999年，Birnbaum和Lozinskii[16]提出一种基于DP过程的模型计数求解方法，称为CDP(counting models using Davis-Putnam procedure)算法.在CDP算法的求解过程中，对具有n个布尔变量的搜索树进行完全搜索，如果在搜索树的某个分支上存在不满足的子句则放弃这个分支的搜索，对其剪枝；否则，记录该分支的所有可满足赋值个数.目前，许多求解#SAT问题的算法都是以CDP算法为基础的.2000年，Bayardo和Pehoushek[17]将组件的思想加入到#SAT问题的求解中，将命题公式转换成约束图的形式来表示：图中的顶点为出现在公式中的变量，若2个变量出现在同一子句中，则在图中代表这2个变量的顶点之间就存在一条边.通过这种方式可以将命题公式分解为多个不相关的子公式，并对这些子公式分别进行求解.然而，在求解各子公式过程中，可能出现之前已经计算过的子公式，如果能在第1次计算时将结果记录下来，则在后续的求解过程中遇到相同的子公式，可以直接使用已经记录的结果，避免重复计算.基于此，Bacchus等人[18]将高速缓存技术引入到了#SAT问题求解中提高了求解效率.Sang等人[19]提出的Cachet方法同时使用了组件缓存和子句学习2种策略.此后Davies和Bacchus[20]在搜索树的每个结点加入更多的推理，如超二元归结和等式约简，使得求解效率有了很大提升.Darwiche[21]利用知识编译的方法来求解#SAT问题，将CNF(conjunctive normal form)公式转化成可分解的、确定的d-DNNF(deterministic,decomposable negation normal form)公式来求解模型个数.以上的算法都是完备性算法，即可以得到精确的模型个数.在#SAT问题求解算法中还存在着一类近似求解的非完备性算法.近似算法主要是基于采样的思想，如ApproxCount算法[22].该方法从原公式选取若干变量组成子空间，并求出该空间精确模型个数，然后通过采样得出总模型个数与子空间模型个数的近似比例，根据此比例和子空间的精确模型个数求出原公式总模型个数近似解.虽然近似算法在大规模问题中有着较好效率，但在许多情况下，需要知道问题的精确模型个数，必须通过完备算法进行求解.甚至，在ApproxCount算法近似求解的过程中，也需要通过精确算法求出子空间的模型个数.因此，对#SAT问题的完备性算法研究有着重要意义.

以上求解#SAT问题的完备性方法基本上都是以归结原理为基础推理方法的.归结原理的基本思想是通过推出空子句的方法来判定给定子句集的不可满足性.然而，与归结方法相反，扩展规则方法通过推出所有极大项组成的集合判定给定子句集的不可满足性[23].基于扩展规则的定理证明方法已经得到了许多相关研究人员的重视,如将扩展规则改进应用到模态逻辑的自动定理证明中[24]；结合扩展规则的知识编译方法[25]；对基于扩展规则方法进行改进提出NER,SER,IBOHMH_IER等系列算法[26-28].殷明浩等人[29]提出基于扩展规则求解#SAT问题的CER(counting models using extension rules)方法.与其他的#SAT求解方法需找出哪些赋值是给定子句集的模型不同，该方法需找出不是子句集模型的赋值，可以看作是基于归结的求解#SAT问题方法的一种补方法.CER方法的基本思想是计算给定子句集所能扩展出的所有极大项个数，进而得出模型个数.这种求解模型计数的方法受到原子句集中互补对个数的影响，当互补对个数较多时该方法一般要优于基于归结的方法，反之当互补对个数较少时要差于基于归结的方法.

本文在充分吸收国内外研究成果的基础上，分析基于扩展规则的求解#SAT问题CER方法的优势与不足，对其进行改进，提出一种基于极大互补度的模型计数新方法，结合带有终止结点的集合枚举树(set enumeration tree, SE-Tree)形式化地表达求解过程，逐步计算给定子句集所能扩展的极大项个数，避免了大部分“无用”结点的生成，从而提高求解效率.

1扩展规则

本节将主要介绍扩展规则及其相关概念和定理.首先对在本文中使用的一些符号做出如下规定：xi(i=1,2,…,m)表示布尔变量；X={x1,x2,…,xm}表示变量集合；用li表示文字，分为正文字和负文字，xi表示变量xi的正文字，xi表示变量xi的负文字；Ci(i=1,2,…,n)表示子句，由文字的析取构成，可将其看成是文字的集合；Φ，Φ′表示CNF公式，由子句的合取构成，可将其看成是子句的集合.

扩展规则是与归结原理“互补”的推理规则，其定义如下：

定义1[23].对于一个给定的子句C和一个布尔变量集合X，子句C中出现的变量包含于变量集合X中，则有子句集合D={C∨x,C∨x|x∈X并且x的正负文字都不出现在子句C中}，将C到D中元素的推导过程叫作扩展规则，D中的元素叫作子句C应用扩展规则的结果.

例1. 给定子句C=x1∨x2∨x3与变量集合X={x1,x2,x3,x4}，则D={x1∨x2∨x3∨x4,x1∨x2∨x3∨x4}就是子句C应用扩展规则后的结果.

定理1[23].子句C与其应用扩展规则后的结果D是等价的.

由扩展规则及定理1可知，一个子句可以被扩展成一个与其等价的子句集.那么，可以对给定子句集中的所有子句应用扩展规则，从而得到一个与原子句集等价的新子句集.

定义2[29].一个非重言式子句是变量集合X上的极大项当且仅当它包含集合X中的所有变量的正文字或其负文字.

若对一个子句不断应用扩展规则，最终将得到一个仅由极大项构成的子句集.由极大项性质可知，对于一个变量集合上的每个极大项来说，在全部赋值空间中有且仅有一个赋值使得其为假，并且一个赋值能且只能使一个极大项为假.这就使得极大项与赋值之间有一个一一对应的关系.

2CER方法

假设给定一个只包含极大项的子句集合Φ，且极大项C包含在子句集Φ中，由于极大项与唯一的一个赋值对应，且使其为假，规定使极大项C为假的赋值为I，那么赋值I也一定使子句集为假.即子句集Φ中包含多少个极大项，就会有多少个赋值使其为假，反之，其不包含的极大项数目就是模型个数.由此给出如下定理：

定理2[29].给定一个子句集Φ，其中所有变量集合是X，且Φ中所有子句都是X上的极大项，那么子句集Φ的模型个数为2|X|-|Φ|，其中|X|表示集合X中变量个数，|Φ|表示子句集Φ中子句个数.

特殊地，当只包含极大项的子句集Φ不可满足时，模型个数2|X|-|Φ|=0，即Φ中包含所有的2|X|个极大项.

由扩展规则可知，一个子句集可以扩展成只包含极大项的集合，如此，再利用定理2即可计算出子句集的模型个数.然而，直接用扩展规则将子句集扩展成只包含极大项的形式是不明智的，实际上，只需要知道子句集能扩展出的极大项个数即可计算出子句集的模型个数，然而，子句集中所有子句扩展出的极大项集合的并集就是子句集能扩展出的极大项集合，即S=|P1∪P2∪…∪Pn|，其中S表示子句集Φ={C1,C2,…,Cn}可扩展出的极大项个数，Pi表示子句Ci可扩展出的极大项集合，其中i=1,2,…,n.

定理3[23].2个子句扩展出的极大项集合不含交集当且仅当这2个子句含有互补文字.

结合包含排斥原理[30]可以得到式(1)来计算子句集所能扩展出的极大项个数，详情可参照文献[23].

(-1)n-1|P1∩P2∩…∩Pn|,

(1)

其中,

S表示子句集Φ={C1,C2,…,Cn}可扩展出的极大项个数，X为变量集合.Pi表示子句Ci可扩展出的极大项集合，i=1,2,…,n.在CER方法中，首先通过式(1)计算出给定子句集可扩展出的极大项个数S，再由定理2即可得到子句集的模型个数2|X|-S.

从式(1)容易看出，当含有互补文字的子句对较多时，式(1)中的值为0的项就较多，显然这些项不用计算，因此算法的效率就较高.为了权衡子句集中这样的含有互补文字的子句对的多少，引入互补因子的概念如下：

定义3[23].给定一个子句集Φ={C1,C2,…,Cn}，Φ的互补因子(complementary factor)是含有互补文字的子句对个数与所有子句对个数之比，即T(n(n-1)2)，其中T表示含互补文字的子句对个数.

CER方法受互补因子的影响，当互补因子较高时算法效率较高，当互补因子降低时算法效率也会随之降低.但是，CER方法中简单地利用式(1)按照分层计算的方式，并没有很好地利用子句间含有互补文字的情况来简化计算过程.基于此，本文对其进行改进，提出了基于互补度的求解方法.

3结合互补度的求解方法

在给出基于互补度的求解方法之前，下面先给出互补度定义及其相关概念.

3.1互补度概念

定义4. 给定子句集Φ，C∈Φ，则称子句集Φ中与子句C含有互补文字的子句个数为子句C的互补度，记为Com_D(C,Φ).

例2. 给定子句集Φ={x1∨x2∨x3,x1∨x3,x1∨x2},子句集Φ中子句x1∨x2∨x3的度为Com_D(x1∨x2∨x3,Φ)=2，同样地,Com_D(x1∨x3,Φ)=1，Com_D(x1∨x2,Φ)=1.

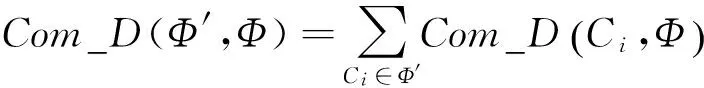
命题1. 给定子句集Φ，若Φ的一个子集Φ′中子句所扩展出的极大项集合交集为空，则任何Φ′的超集中子句扩展出的极大项集合的交集也为空.

命题2. 给定子句集Φ，若Φ的一个子集Φ′的互补度Com_D(Φ′,Φ)=0，则Φ′中必不含有互补文字.

显然，对含有互补文字的子句子集及其超集对应的式(1)中计算项是没有必要求值的.那么，若可以提前找到含互补文字的最小子句集(即不是任何含有互补文字的子句集的超集)并忽略掉它的超集，则可避免对这些超集判断是否含互补文字的计算.基于此，提出一种结合SE-Tree的基于互补度的#SAT求解方法.

3.2CDCER(complementary-degree-based CER)

方法

SE-Tree是由Rymon[31]提出的一种用于列举一个集合的幂集中元素的树型数据结构：一个完全的SE-Tree按照一定的顺序(如数字、字母顺序等)可以列举出一个集合的幂集中所有的元素集合.如一个包含4个子句的子句集Φ={C1,C2,C3,C4}，它的完全集合枚举树如图1所示:

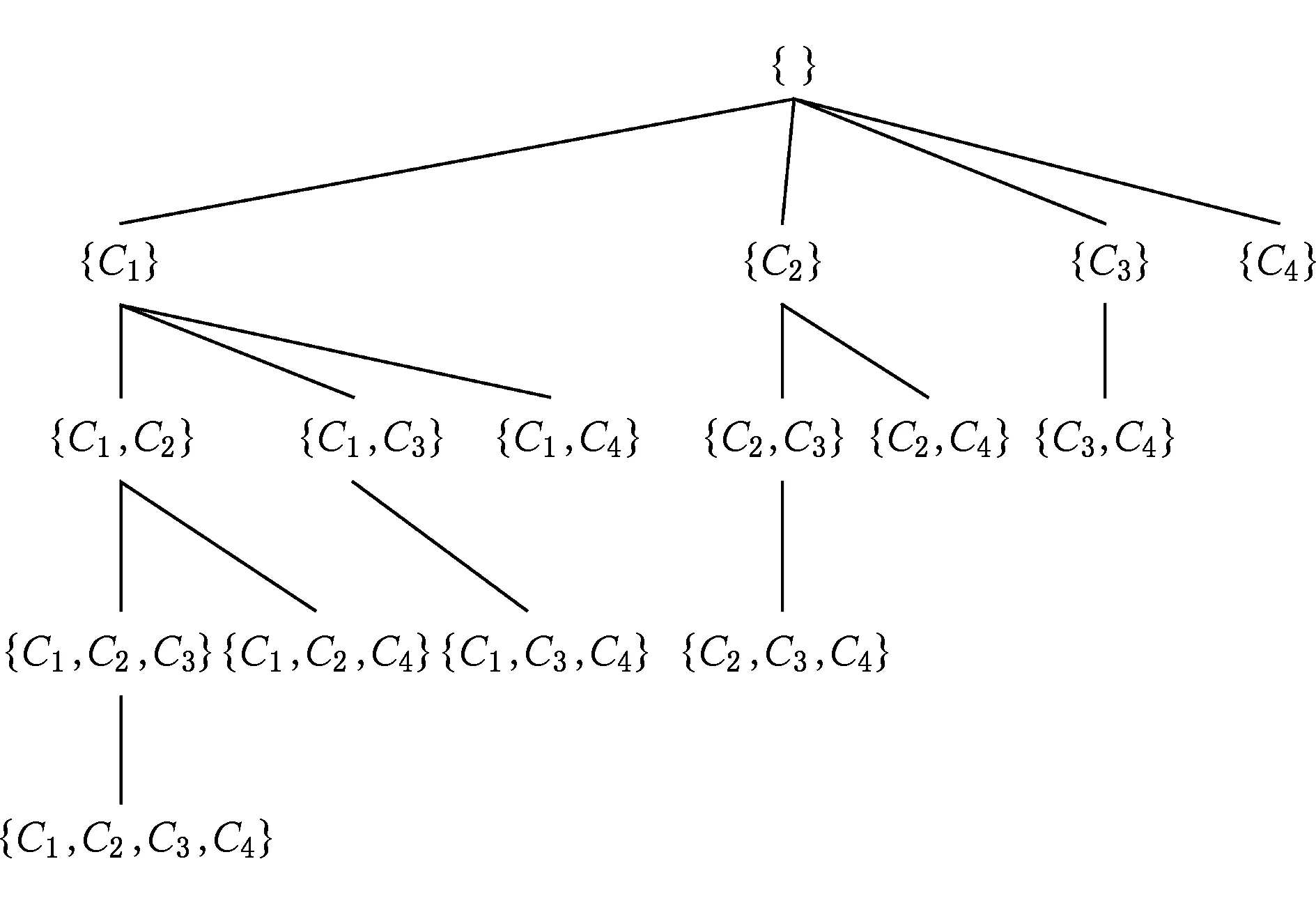
Fig. 1　The SE-Tree of {C1,C2,C3,C4}.图1　子句集{C1,C2,C3,C4}的完全集合枚举树

CER方法中，求解子句集Φ={C1,C2,…,Cn}的模型个数即为计算式(2)的值：

(2)

式(2)中每一项都与子句集Φ的一个子集相对应，如|Pi∩Pj∩…∩Pk|是子句集{Ci,Cj,…,Ck}中子句扩展出的极大项集合交集的大小.特殊地，2|X|与空子集相对应.式(2)中每一项都与子句集Φ的SE-Tree中结点对应.

CDCER方法的基本思想如下：使用SE-Tree按照集合长度由小到大的顺序逐步生成给定子句集的子集，计算每个结点的子结点互补度，按照互补度由大到小的顺序生成子结点.判断结点子句集中是否含有互补文字，如果有则对枚举树剪枝；否则统计结点中文字个数W，计算2|X|-W，将结果进行累加(或累减)，并将这样生成的树记为CDSE-Tree(complementary-degree-based SE-Tree).

例3. 给定子句集Φ={C1,C2,C3,C4}，其中含有互补文字的子句对有(C1,C4),(C2,C4),(C2,C3),(C3,C4)，即Com_D(C1,Φ)=1，Com_D(C2,Φ)=2，Com_D(C3,Φ)=2，Com_D(C4,Φ)=3.未结合互补度进行剪枝生成的SE-Tree如图2(a)所示，SE-Tree生成13个结点，其中2个结点被剪枝；按照互补度由大到小顺序生成的CDSE-Tree如图2(b)所示，CDSE-Tree生成10个结点，其中3个结点被剪枝；相比没有加入互补度的SE-Tree，CDSE-Tree中剪掉了更多冗余结点.

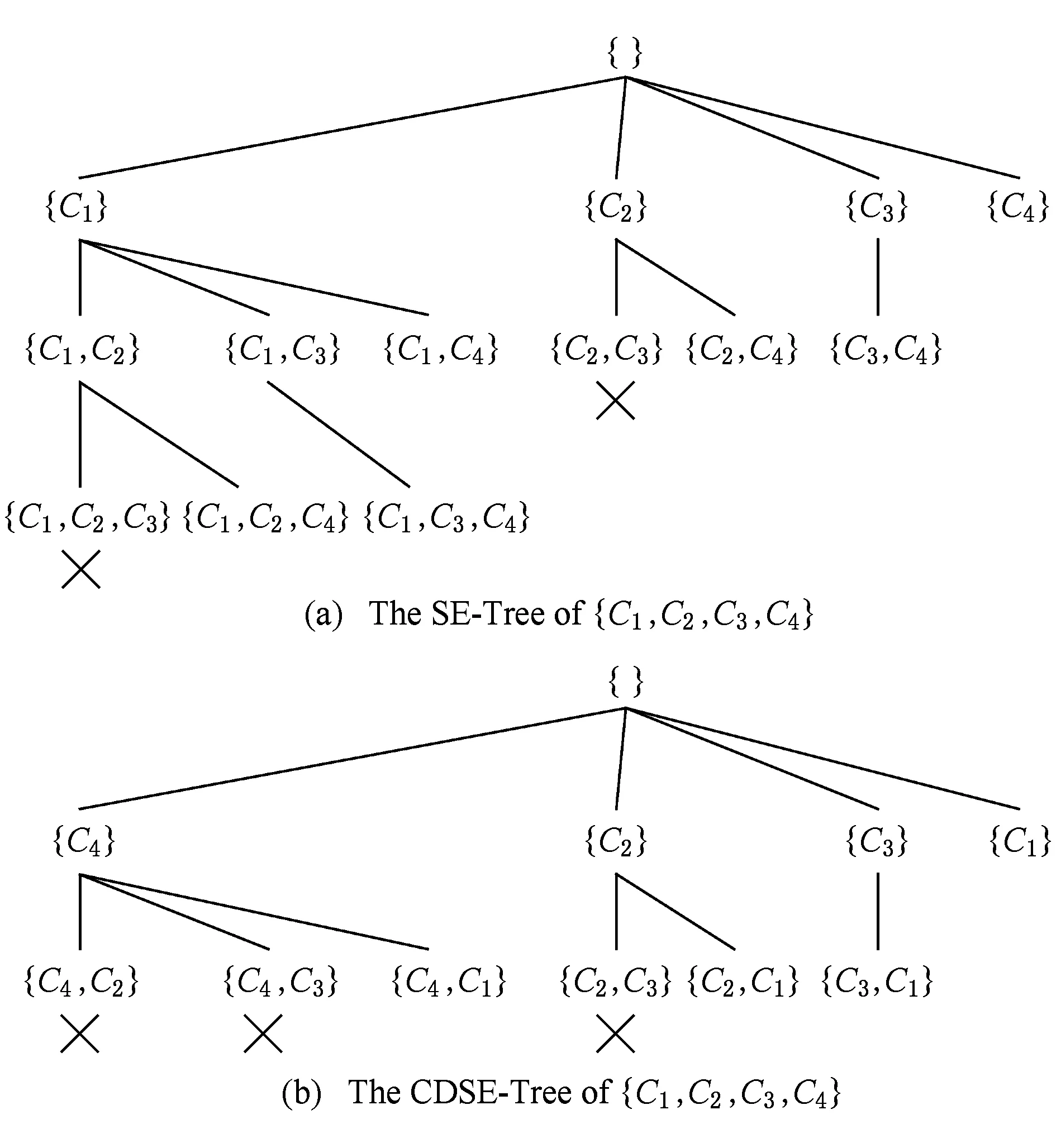
Fig. 2　Comparison of SE-Tree and CDSE-Tree of {C1,C2,C3,C4}.图2　子句集{C1,C2,C3,C4}的SE-Tree与CDSE-Tree比较

基于互补度的CDCER方法通过CDSE-Tree描述计算过程，可以避免更多值为0的冗余的计算项生成，减少对相应子句集判断是否含有互补文字的计算，从而提高了算法的求解效率.具体算法如下：

算法1. CDCER(Φ,X).

输入：子句集Φ、变量集合X；

输出：子句集Φ的模型个数.

①num_model=0;

②Node←∅;

③ For (当前互补度最大的结点Node)

④ Begin

⑤ If (Com_D(Node,Φ)=-1)

⑥ Break;

⑦ EndIf

⑧ If(Com_D(Node,Φ)>0并且Node中有互补文字)

⑨Com_D(Node,Φ)=-1;

⑩ Continue;

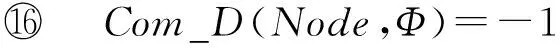
算法1开始时，当前结点为根结点，即空集.若当前结点含有互补文字，则直接将其互补度置为-1并剪枝，继续找互补度最大的结点.否则，计算结点中子句能扩展出的极大项集合交集的大小，结点在偶数层(其中有偶数个子句)则将结果累加，在奇数层则累减.然后，将结点互补度置为-1，并扩展其子结点.若当前结点中互补度最大为-1，则表示CDSE-Tree中所有“有效”结点已经扩展完.由命题2可知，若当前结点中互补度最大为0，如根结点，则结点中必没有互补文字，可直接对其计算无需判断是否含有互补文字.

下面从理论上对算法1做相应分析：

1) 修剪规则的正确性.在CDCER方法中，对每一个已经产生的结点子句集(除根结点)都需要判定结点中是否包含互补文字，即结点中是否包含一对含有互补文字的子句.若包含，则由定理3可知，结点中子句扩展出的极大项集合的交集为空集，在式(2)中此结点相对应的计算项值为0，那么不对此计算项进行求解也不会影响求解结果.在CDCER方法中对此类结点进行剪枝.若结点不包含互补文字，则结点中子句扩展出的极大项集合的交集为非空集合，需要对其进行相应求值计算.由命题1可知，若子句集中含有互补文字，则其任意超集中子句扩展出的极大项集合的交集必为空集.然而在CDSE-Tree中，一个结点的所有子孙结点都是该结点的超集，那么若当前结点中含有互补文字，结点计算结果为0，则其子孙结点也必是包含互补文字的冗余结点，不需要对它们进行求解，对这样的结点剪枝将不会影响求解结果，保证了修剪规则的正确性.

2) 完备性.一个完全的SE-Tree能够按照某种预定的顺序枚举出一个集合的所有子集，CDCER方法结合SE-Tree按照集合长度由小到大和互补度由大到小的顺序逐步生成给定子句集的子集.若不存在剪枝的情况，那么最后生成的完全CDSE-Tree将枚举出给定子句集的所有子集.由包含排斥原理的知识可知，式(2)中所有计算项与给定子句集的所有子集是一一对应的关系.然而CDCER方法中的剪枝规则只是修剪掉了CDSE-Tree中的冗余结点，即在式(2)中相应地去掉值为0的计算项，并不会对求解结果的正确性产生影响.所以CDCER方法必将求解出全部的模型个数.

以上部分给出了本文提出的基于互补度的#SAT求解方法CDCER方法，并用SE-Tree描述算法求解过程；CDCER方法减少了判断子句间是否含有互补文字的计算，从而提高了算法的效率.

4实验结果分析

本节给出CDCER方法在随机问题上的实验测试结果，并将其与CER方法进行比较.实验平台如下: Windows XP操作系统,CPU AMD AthlonTM64 X2 Dual Core Processor 3600+ 1.9 GHz,2.00 GB RAM.

之所以选择随机问题是为了方便控制生成用例的类型，如互补因子.实验用例由随机生成器产生,其输入参数有变量个数m、子句个数n以及变量在各子句中的出现概率p,每个子句都按一定概率p从m个变量中选取变量,因变量的正负文字相对于子句集来说是对称的,所以这里只控制变量为正的概率p′,p′范围是(0.1,0.5).本文的实验数据采用变量个数为30、子句个数为100的随机样例进行实验测试.通过限定变量在子句中出现概率并结合其正文字出现概率来限定子句集中子句的平均子句长度以及互补因子的大小,实验测试互补因子范围为0.1～0.9,实验结果是10次实验的平均结果.CER与CDCER方法对于随机问题的实验结果如表1所示.

表1给出了2种方法对于各测试用例的求解时间及两者时间差(CER方法的求解时间减去CDCER方法的求解时间)、求解过程中需要扩展的结点数(需生成的子句集合数)及其差值(CER方法需扩展的结点数量减去CDCER方法的结点数)，时间单位为s.从表1的结果可以看出，随着互补因子的增大，2种方法的求解时间都相对减少，且CDCER方法的求解效率普遍要优于CER方法.这是因为一般情况下CDCER方法与CER方法中所需扩展的结点数的差值较大，而CDCER方法恰恰节省了对这些CER方法中多扩展出的结点判断是否含有互补文字的时间，所以效率一般要优于CER方法.

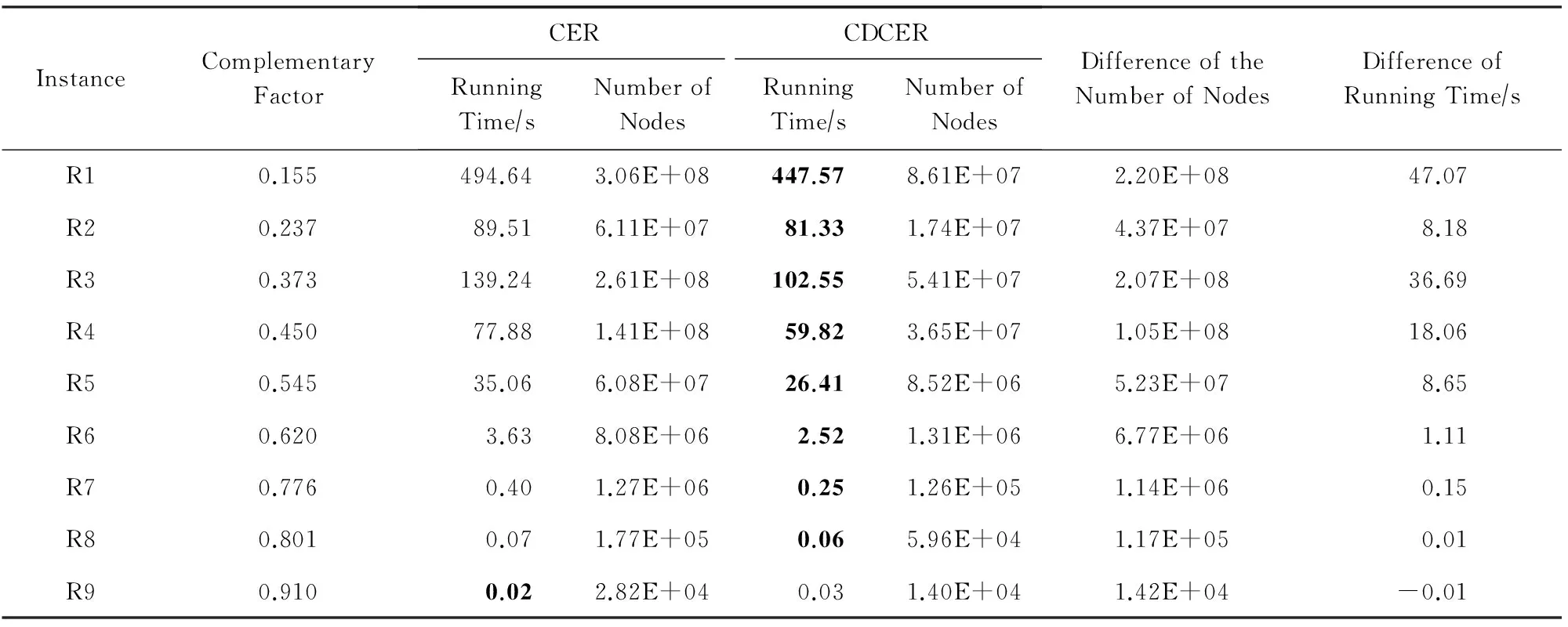
Table 1　The Comparison of Running Time Cost in CER and CDCER

Note: Each instance contains 30 variables and 100 clauses.

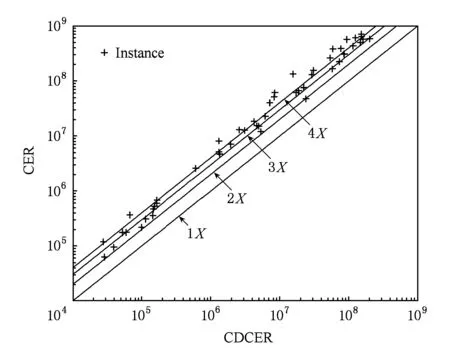
Fig. 3　Comparison of number of nodes extended in CER and CDCER.图3　CER和CDCER方法运行过程中扩展结点数对比图

此外，随着互补因子的增大，2种方法需要扩展的结点数量都相对减少，并且两者的差值也随之减小.而相比CER方法，CDCER方法求解时间降低的多少与结点数量差值大小有着直接关系，随着差值减小，2种方法的时间差也随之减少.在互补因子很高的特殊情况下，如表1中测试用例R9，CER方法中需要扩展的结点数很少，CDCER方法与CER方法需扩展的结点数差值较小.此时，CDCER方法对子句互补度的计算抵消了由结点数减少带来的效率提升，故其效率低于CER方法.但在这种特殊情况下CER方法求解时间已经很少，算法效率的提升空间已经很小，而CDCER方法的求解效率也较高.下面给出2种方法求解过程中扩展结点数的对比，如图3所示：

图3中散点表示测试用例，是随机生成的变量数为30、子句个数为100的50个随机测试用例.横竖坐标分别表示CDCER和CER两种方法运行过程中扩展的结点数.从图3可以看出，对于所有测试用例CDCER方法求解过程中生成的结点都远少于CER方法.对于大部分测试用例CER方法求解过程中扩展的结点数是CDCER方法中结点数的3～4倍(图3中大部分散点落于3倍线，甚至4倍线之上)，甚至更高.相对于CER方法，CDCER方法运行过程中扩展的结点数减少的越多，其效率提升也就越高.

5结束语

许多学者对#SAT问题的求解方法进行了研究.在CER方法中，利用扩展规则方法求出给定子句集所能扩展出的极大项个数，从而得到不能扩展出的极大项个数，得出求解结果.当互补因子较高时，基于扩展规则的方法一般要优于基于归结的方法；反之，当互补因子较低时，基于扩展规则的方法要差于基于归结的方法.针对此问题本文基于CER方法提出了求解#SAT的CDCER方法，在互补因子较低时较大程度地提高了求解效率.该方法结合SE-Tree形式化描述求解过程，易于理解且编程简单，实现时并不用构造树.在枚举树生成结点时，按照结点的互补度由大到小的顺序生成结点，尽可能早地生成含有互补文字的结点，有效地减少了枚举树中扩展出的冗余结点个数，避免了对大部分冗余结点是否含有互补文字的判断.还给出了CDCER方法的正确性和完备性证明，实验结果表明该方法效率较高.

致谢全体作者对本文所有匿名审稿人的辛勤工作和提出的宝贵意见表示真挚感谢！

参考文献

[1]Rintanen J. Planning as satisfiability: Heuristics[J]. Artificial Intelligence, 2012, 193: 45-86

[2]Grastien A, Anbulagan A. Diagnosis of discrete event systems using satisfiability algorithms: A theoretical and empirical study[J]. IEEE Trans on Automatic Control, 2013, 58(12): 3070-3083

[3]Biere A, Cimatti A, Clarke E M, et al. Symbolic model checking using SAT procedures instead of BDDs[C]Proc of the 36th Annual ACMIEEE Design Automation Conf. New York: ACM, 1999: 317-320

[4]Monasson R, Zecchina R, Kirkpatrick S, et al. Determining computational complexity from characteristic “phase transitions”[J]. Nature, 1999, 400(6740): 133-137

[5]Mezard M, Parisi G, Zecchina R. Analytic and algorithmic solution of random satisfiability problems[J]. Science, 2002, 297(5582): 812-815

[6]Luo Chuan, Cai Shaowei, Wu Wei, et al. Double configuration checking in stochastic local search for satisfiability[C]Proc of the 28th AAAI Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2014: 2703-2709

[7]Cai Shaowei, Su Kaile. Comprehensive score: Towards efficient local search for SAT with long clauses[C]Proc of the 23rd Int Joint Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2013: 489-495

[8]Davis M, Putnam H. A computing procedure for quantification theory[J]. Journal of the ACM (JACM), 1960, 7(3): 201-215

[9]Cai Shaowei, Su Kaile. Local search for boolean satisfiability with configuration checking and subscore[J]. Artificial Intelligence, 2013, 204: 75-98

[10]Luo Chuan, Cai Shaowei, Su Kaile, et al. Clause states based configuration checking in local search for satisfiability[J]. IEEE Trans on Cybernetics, 2015, 45(5): 1014-1027

[11]Chavira M, Darwiche A. On probabilistic inference by weighted model counting[J]. Artificial Intelligence, 2008, 172(6): 772-799

[12]Sang T, Beame P, Kautz H A. Performing Bayesian inference by weighted model counting[C]Proc of the 20th National Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2005: 475-481[13]Majercik S M, Littman M L. Contingent planning under uncertainty via stochastic satisfiability[J]. Artificial Intelligence, 2003, 147(1): 119-162[14]Bacchus F, Dalmao S, Pitassi T. Algorithms and complexity results for #SAT and Bayesian inference[C]Proc of the 44th Symp on Foundations of Computer Science. Los Alamitos, CA: IEEE Computer Society, 2003: 340-351[15]Zhou Junping, Yin Minghao, Zhou Chunguang. New worst-case upper bound for #2-SAT and #3-SAT with the number of clauses as the parameter[C]Proc of the 24th AAAI Conf on Artificial Intelligence (AAAI 2010). Menlo Park, CA: AAAI, 2010: 217-222[16]Birnbaum E, Lozinskii E L. The good old Davis-Putnam procedure helps counting models[J]. Journal of Artificial Intelligence Research, 1999, 10(1): 457-477[17]Bayardo Jr R J, Pehoushek J D. Counting models using connected components[C]Proc of the 17th National Conf on Artificial Intelligence (AAAI 2000). Menlo Park, CA: AAAI, 2000: 157-162[18]Bacchus F, Dalmao S, Pitassi T. DPLL with caching: A new algorithm for #SAT and Bayesian inference[J]. Electronic Colloquium on Computational Complexity, 2003, 10: 1-21[19]Sang T, Bacchus F, Beame P, et al. Combining component caching and clause learning for effective model counting[C]Proc of the SAT 2004. Berlin: Springer, 2004: 20-28[20]Davies J, Bacchus F. Using more reasoning to improve #SAT solving[C]Proc of the 22nd National Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2007: 185-190[21]Darwiche A. New advances in compiling CNF into decomposable negation normal form[C]Proc of the 16th European Conf on Artificial Intelligence. Amsterdam: IOS, 2004: 328-332[22]Wei W, Selman B. A new approach to model counting[C]Proc of the SAT 2005. Berlin: Springer, 2005: 324-339[23]Lin Hai, Sun Jigui, Zhang Yimin. Theorem proving based on extension rule[J]. Journal of Automated Reasoning, 2003, 31(1): 11-21[24]Wu Xia, Sun Jigui, Lin Hai, et al. Modal extension rule[J]. Progress in Natural Science, 2005, 15(6): 550-558[25]Lin Hai, Sun Jigui. Knowledge compilation using extension rule[J]. Journal of Automated Reasoning, 2004, 32(2): 93-102[26]Sun Jigui, Li Ying, Zhu Xingjun, et al. A novel theorem proving algorithm based on extension rule[J]. Journal of Computer Research and Development, 2009, 46(1): 9-14 (in Chinese)(孙吉贵, 李莹, 朱兴军, 等. 一种新的基于扩展规则的定理证明算法[J]. 计算机研究与发展, 2009, 46(1): 9-14)[27]Zhang Liming, Ouyang Dantong, Bai Hongtao. Theorem proving algorithm based on semi-extension rule[J]. Journal of Computer Research and Development, 2010, 47(9): 1522-1529 (in Chinese)(张立明, 欧阳丹彤, 白洪涛. 基于半扩展规则的定理证明方法[J]. 计算机研究与发展, 2010, 47(9): 1522-1529)[28]Li Ying, Sun Jigui, Wu Xia, et al. Extension rule algorithms based on IMOM and IBOHM heuristics strategies[J]. Journal of Software, 2009, 20(6): 1521-1527 (in Chinese)(李莹, 孙吉贵, 吴瑕, 等. 基于IMOM和IBOHM启发式策略的扩展规则算法[J]. 软件学报, 2009, 20(6): 1521-1527)[29]Yin Minghao, Lin Hai, Sun Jigui. Solving #SAT using extension rules[J]. Journal of Software, 2009, 20(7): 1714-1725 (in Chinese)(殷明浩, 林海, 孙吉贵. 一种基于扩展规则的#SAT求解系统[J]. 软件学报, 2009, 20(7): 1714-1725)[30]Sun Jigui, Yang Fengjie, Ouyang Dantong, et al. Discrete Mathematics [M]. Beijing: Higher Education Press, 2002 (in Chinese)(孙吉贵, 杨凤杰, 欧阳丹彤, 等. 离散数学[M]. 北京: 高等教育出版社, 2002)[31]Rymon R. Search through systematic set enumeration[C]Proc of the 3rd Int Conf on Principles of Knowledge Representation and Reasoning. San Francisco: Morgan Kaufmann, 1992: 539-550

Ouyang Dantong, born in 1968. Professor and PhD supervisor of Jilin University. Senior member of China Computer Federation. Her main research interests include model-based diagnosis, model checking and automated reasoning.

Jia Fengyu, born in 1991. Master candidate. His main research interests include model-based diagnosis, SAT problem and automated reasoning (jiafy_email@163.com).

Liu Siguang, born in 1988. Master candidate at Jilin University. His main research interests include model-based diagnosis, model checking and automated reasoning (lsgmliss@163.com).

Zhang Liming, born in 1980. PhD, post-doctor in Jilin University. His main research interests include model-based diagnosis, model checking and automated reasoning.

收稿日期：2015-01-12；修回日期：2015-06-02

基金项目：国家自然科学基金项目(61402196,61272208,61133011,61003101,61170092)；中国博士后科学基金项目(2013M541302)；吉林省科技发展计划基金项目(20140520067JH)

通信作者：张立明(limingzhang@jlu.edu.cn)

中图法分类号TP18

An Algorithm Based on Extension Rule For Solving #SAT Using Complementary Degree

Ouyang Dantong, Jia Fengyu, Liu Siguang, and Zhang Liming

(CollegeofComputerScienceandTechnology,JilinUniversity,Changchun130012) (KeyLaboratoryofSymbolicComputationandKnowledgeEngineering(JilinUniversity),MinistryofEducation,Changchun130012)

AbstractThe #SAT problem also called model counting is one of the important and challenging problems in artificial intelligence. It is used widely in the field of artificial intelligence. After doing the in-depth study of model counting algorithm CER that is based on Extension Rule, we propose a method using complementary degree for #SAT problem in this paper. We formalize the computing procedure of solving #SAT problem by introducing SE-Tree which produces all the subsets of clause set that need to be computed. As the closed nodes are added into the SE-Tree, the most subsets that contain complementary literal(s) can never be produced, and the true resolutions cannot be missed by pruning either. Then the concept of complementary degree is presented in this paper, and the nodes of SE-Tree are extended in accordance with the descending order of complementary degree. With this extended order, the subsets that contain complementary literal(s) and have smaller size can not only be generated early, but also can reduce the number of generated nodes that are redundant. Moreover the calculation for deciding the complementarity of subsets is reduced. Results show that the corresponding algorithm runs faster than CER algorithm and further improves the solving efficiency of problems which complementary factor is lower.

Key wordsextension rule; model counting; CER (counting models using extension rules) algorithm; complementary degree; SE-Tree (set enumeration tree)

This work was supported by the National Natural Science Foundation of China (61402196,61272208,61133011,61003101,61170092), the China Postdoctoral Science Foundation (2013M541302), and the Jilin Province Science and Technology Development Plan (20140520067JH).