求解约束可满足问题的eSTR算法优化

王瑞伟　李占山　李宏博

1(符号计算与知识工程教育部重点实验室(吉林大学)　长春　130012)2(吉林大学计算机科学与技术学院　长春　130012)3　　　(吉林大学软件学院　长春　130012)



求解约束可满足问题的eSTR算法优化

王瑞伟1,3李占山1,2,3李宏博1,2

1(符号计算与知识工程教育部重点实验室(吉林大学)长春130012)2(吉林大学计算机科学与技术学院长春130012)3(吉林大学软件学院长春130012)

(120801104@qq.com)

摘要表约束方法是1种外延式知识表示方法，每个约束通过元组集直接枚举出其在1个变量集上允许或禁止的所有元组，直观易于理解，在约束程序中得到了深入的研究，这是因为表约束出现在如设计、数据库、配置以及偏好建模等许多现实世界的应用中.但随着约束的增多及其元组集增大，占有的空间与相容性检测效率成了关键问题.eSTR是1个将STR扩展到高阶相容的算法，通过深入分析eSTR算法后发现有2种优化方式:PWsup数据结构和极小约束范围，同时证明了在极小约束范围上，约束网络仍然能够维持PWC+GAC，其中极小约束范围可以通过删除约束元组集中相应的列来降低eSTR2算法的空间消耗，而PWsup数据结构能够通过避免不必要的PW支持检测来减少eSTR2的CPU运行时间，实验结果表明：2种优化方式和eSTR2相结合后能够同时减少算法的空间消耗和CPU运行时间，在许多类实例上明显优于eSTR2和eSTR2w.

关键词高阶相容；极小约束范围；约束网络；PWsup数据结构；PWC+GAC

作为人工智能一个主要研究分支的约束程序(constraint programming， CP) 兴起于20世纪80年代末期，1996年美国计算机学会(Association for Computing Machinery, ACM) 在庆祝其成立50周年的大会上，将CP确立为21世纪计算机科学最有前途的战略研究方向之一.正如其所预言的那样，进入21世纪后，CP的理论研究与应用出现了1个高潮：近年来召开的IJCAI,AAAI,ECAI等顶级国际会议都把相关问题研究作为会议的1个重要议题.最近几年在设计、数据库、配置和偏好建模等领域有着重要应用的表约束求解方法受到了大量学者的关注.表约束方法是1种外延式知识表示方法，每个约束通过元组集直接枚举出其在1个变量集上允许或禁止的所有元组，非常地直观，但随着约束的增多及其元组集增大占有的空间与相容性检测效率成了关键问题.为此许多学者对此开展了大量研究工作.在表压缩方面，如在表约束上维持GAC的高效算法有STR2[1],MDDC[2].其中2011年法国学者Lecoutre[1]提出的STR2是动态维持允许元组集算法STR的更精化版本，被认为是在多元正表约束上最有效的GAC(generalized arc-consistency)算法；2010年Cheng和Yap[2]提出的基于多元决策图的MDDC方法是二元决策图方法的1种推广，适合于正表与负表约束二种知识表示的压缩，尤其当元组集中各个元组之间具有许多交叠部分时MDDC要优于STR2；2013年Xia和Yap[3]提出的STR2-C将STR2的思想与笛卡儿积压缩表[4]相结合，在压缩率较高的问题上STR2-C时间和空间效率都要优于STR2；Jefferson和Nightingale[5]提出的SHORT-STR2利用元组集上的一些特性将一些元组转化为短约束元组来减少元组集的行数(元组个数)，从而提高STR2的算法时间和空间效率；国内研究者李宏博等人[6]在2013年提出了STR-N，将STR算法扩展到负表约束.其他一些国内学者主要研究的是约束满足问题Benchmark模型生成或二元约束求解问题，如北京航空航天大学许可等人[7-8]提出了生成随机约束可满足问题benchmark实例的模型方法被广泛应用于benchmark实验测试中；李宏博等人[9]研究了二元约束上的粗粒度弧相容算法的优化问题，指出对于指向已赋值变量的弧存在无效的修正检查并证明了这类修正检查是冗余的，提出了1种方法来避免这类冗余的修正检查方法；李占山等人[10]提出了用于回溯搜索的新启发式；中国科学院软件研究所张健等人[11-12]研究了约束满足问题与组合优化的关系问题和拉丁方问题，在文献[11]中张健等人提出了将混合约束问题转化为混合整数规划问题的方法，用约束求解方法及混合整数规划方法共同求解混合约束问题；在文献[12]中张健等人描述了双自成正交拉丁方的搜索方法，目前国内研究表约束方法的人还较少.

另外1个受关注的表约束问题是维持高阶相容性，高阶相容性主要是通过求解特定的子问题来化简整个问题的变量域或约束元组集，目前人们已经提出了许多不同的高阶相容性方法，如1989年Janssen等人[13]提出的PWC(pair-wise consistency)构建的子问题是约束元组集中元组能否扩展到所有相邻约束，同时还给出1种删多余边的方式来减少相邻约束数量即化简所构建的子问题；maxRPWC是Bessiere等人[14]在2008年提出的高阶域过滤相容性，主要是确保变量值在包含该变量的约束元组集中存在1个能扩展到所有相邻约束的GAC支持，在稀疏问题或较大定义域问题上maxRPWC优于GAC；Paparrizou等人[15]在2012年给出在表约束上维持maxRPWC的高效算法同时提出了maxRPWC+，maxRPWC+忽略掉那些因为元组失去PW(pair-wise)支持带来的约束传播，在他们所测的大多数问题上maxRPWC+要优于maxRPWC；2010年Karakashian等人[16]提出维持R(*m)C的高效算法，R(*m)C将约束元组集中不能同时扩展到其他任意m-1个约束上的元组删掉，在困难问题上R(*m)C优于GAC；eSTR是2013年Lecoutre等人[17]提出的在表约束上维持PWC+GAC的高效算法，PWC所构造的子问题是元组能否扩展到所有相邻约束上，eSTR利用计数器来实时记录元组在各个相邻约束上的支持个数，从而能够在常量时间内判断是否存在PW支持，它大幅度降低了搜索子问题解带来的时间消耗，在许多类问题上能够比maxRPWC+和STR2算法更有效率.但在高阶相容性算法中很难像STR2-C和SHORT-STR2一样通过压缩元组集的行数(元组数)来降低算法的时间和空间消耗，因为目前大多数高阶相容性构造的子问题会考虑到单个元组的特性，将多个元组压成1行后，在求解子问题时还得分开考虑，很难一起处理多个元组，为此本文提出1种压缩元组集列数的方式来降低eSTR算法的时间和空间消耗，另外在eSTR算法检测PW支持时，进行了许多冗余的检测，相应的本文给出1种忽略冗余检测的优化方式来提高eSTR算法的时间效率.本文阐述的主要工作有2点：

1) 在检测约束中元组是否在相邻约束上有PW支持时，并不检测所有的相邻约束而只检测可能使当前约束中元组失去PW支持的相邻约束，本文采用PWsup数据结构来记录需要检测的相邻约束，减少约束检查次数提高eSTR算法的时间效率.

2) 在维持PWC后，一些约束的约束范围中存在多余变量，本文删掉约束范围中的多余变量得到极小约束范围来降低eSTR算法的时间消耗，同时在删完多余变量及初始化ctr计数器后可以直接删掉对应元组集中的列来降低eSTR算法的空间消耗.

1背景知识

约束可满足问题定义为1个三元组(X，D，C)，其中X={x1,x2,…,xn}是1个由n个变量组成的集合，D={D(x1),D(x2),…,D(xn)}是有限域的集合，每个变量对应1个域;C={c1,c2,…,ce}是e个约束组成的集合，其中每个约束都和变量子集scp(c)相对应，称scp(c)为约束范围，同时每个表约束还有1个相对应的元组集rel(c).

人们经常使用的局部相容性是广义弧相容(GAC)，1个变量值(x,a)是GAC的,当且仅当∀c∈C且x∈scp(c),∃τ∈rel(c),使得τ(x)=a且τ是有效的，则称τ是a在c上的支持.1个变量x是GAC，当且仅当∀a∈D(x),(x,a)是GAC的，1个约束可满足问题是GAC的，当且仅当∀x∈X是GAC的.

GAC是域相容，它通过删除不相容的变量值来维持相容性，而关系相容是通过删除不相容的元组来达到相容，PWC是关系相容，它确定了元组需要满足的性质.1个元组(c,τ)是PWC的，当且仅当τ在所有和c相邻的约束上有PW支持.1个约束c是PWC的，当且仅当∀τ∈rel(c)是PWC的，1个约束可满足问题是PWC的，当且仅当∀c∈C是PWC的.元组τ在相邻约束上存在PW支持是指在相邻约束上存在和τ相交部分相等的元组.本文只考虑约束范围交集中变量数大于1的相邻约束，因为约束网络维持GAC后在交集变量数为1的相邻约束上一定有PW支持.

eSTR算法中最主要的数据结构是ctr[c][c′][k]计数器，其用于记录约束c的元组集在c和c′的约束范围交集中变量上投影得到的集合中第k个元素在约束c当前元组集上的支持个数，若ctr[c][c′][k]=0则说明投影得到的集合中第k个元素在约束c的当前元组集中不存在支持,这说明在约束c′中存在ctr[c′][c][ctrlink[c][c′][k]]个元组在约束c上失去PW支持[17].

2PWsup数据结构

STR2能够有效地减少元组中变量值的有效性检测，因为它只检测可能变为无效的变量值，相应地检测元组的PW支持也可以只检测那些可能会失去PW支持的相邻约束.为此，我们引入1个新的数据结构PWsup，PWsup[c]用于记录约束c中元组在哪些相邻约束上可能会失去PW支持.

算法1只检测约束c中元组在PWsup[c]中约束上是否存在PW支持，若是在PWsup[c]中的约束上都存在PW支持那么就认为该元组是PWC相容的，因为PWsup[c]中包含了所有c在其上可能失去PW支持的相邻约束，只要元组τ在PWsup[c]中的约束上存在PW支持，那么τ在c的所有相邻约束上都存在PW支持.应用PWsup[c]数据结构最重要的1点是保证PWsup[c]包含所有可能使c在其上失去PW支持的相邻的约束.

算法1. 检测PW支持.

isPWconsistent(c,index):Boolean

① begin

② for eachc′∈PWsup[c] do

③j←ctrIndexes[c][c′][index];

④k←ctrlink[c][c′][j];

⑤ ifk=NULL ORctr[c′][c][k]=0 then

⑥ return FALSE;

⑦ end if

⑧ end for

⑨ return TRUE;

⑩ end

本文通过4种方式来维持PWsup[c]数据结构：

1) 初始化时PWsup[c]={所有和c相邻且变量交集大于1的约束}.

2) 删掉c中所有不相容的元组后将PWsup[c]清空，因为此时c中元组在所有的相邻约束上必然存在PW支持.

3) 当发生回溯而恢复现场时，清空PWsup[c]，因为在进入下1层之前，整个约束网络要先维持GAC+PWC，也就是说回复现场后c中元组在所有相邻的约束上都存在PW支持，所以清空PWsup[c].

4) 在算法2中更新ctr计数器时，通过ctr计数器的值判断是否会引起相邻约束中元组在c上失去PW支持，若是相邻约束c′有元组在c上失去了PW支持，那么相应地将c加入PWsup[c′]中，这样我们就能保证PWsup[c′]包含所有可能使c′在其上失去PW支持且和c′相邻的约束，具体见算法2.

算法2. 更新ctr计数器.

updateCtr(c,index)

① begin

② for eachc′≠cand |scp(c′)∩scp(c)|>1 do

③j←ctrIndexes[c][c′][index];

④ctr[c][c′][j]←ctr[c][c′][j]-1;

⑤ ifctr[c][c′][j]=0 then

⑥k←ctrlink[c][c′][j];

⑦ ifk≠NULL ORctr[c′][c][k]>0 then

⑧ addc′ toQ;

⑨PWsup[c′]←PWsup[c′]∪c;

⑩ end if

在算法2中行⑦，当ctr[c′][c][k]>0时将c′加入传播队列Q中并将c加入PWsup[c′]中，而在原来的eSTR算法[17]中，当ctr[c][c′][j]=0时就将c′加入Q，这使得算法进行了许多没有必要的约束传播，算法2是本文优化后的结果.

维持PWsup[c]数据结构后，约束c只需进行O(pt)次PW支持检测就能够维持PWC，其中p是PWsup[c]中包含的相邻约束个数，回溯算法进入下1层之前约束网络总是先维持PWC+GAC，这时PWsup[c]为空，也就是说不用检测PW支持，若没有PWsup数据结构，我们就得进行O(gt)次PW支持检测，其中g是指和c相邻的约束范围交集中变量个数大于1的约束数量，t是指约束表中的元组数量.另外维护数据结构PWsup的时间消耗是O(gt+p)，O(p)是每次清空数据结构的时间消耗，O(gt)是算法2中行⑨所带来的消耗，幸运的是我们只有满足条件ctr[c][c′][j]=0和ctr[c′][c][k]>0后才会进行更新而且每次更新的时间消耗都很少，所以通常维持数据结构的时间很少，此外PWsup数据结构消耗的空间复杂度是O(e2).

3极小约束范围及其应用示例

dual图是1个以约束为结点并在任意2个约束范围交集不为空的的结点之间添加边后得到的图，dual图中的2个结点间的1条边是多余边，当且仅当存在1条替代路径连接这2个结点且路径中每个结点的约束范围都包含这2个结点的约束范围交集中所有变量，删去多余边后约束网络依然能够维持PWC[13].本文提出和多余边相类似的多余变量，将约束范围中的多余变量删掉以后，约束网络依然能够维持PWC+GAC.

定义1. 约束网络N所对应的 2-dual图是指将N对应的dual图中变量数小于2的边去掉得到的图.

图1(a)给出了1个约束网络，同时图1(b)是其对应的2-dual图，我们可以发现其实2-dual图其实就是以约束为结点集，在任意2个约束范围交集中变量数大于1的约束之间存在1条边的图.

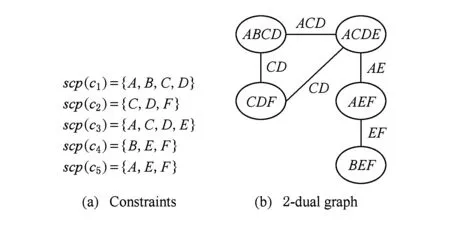
Fig. 1　A constraint network and 2-dual graph.图 1　1个约束网络和2-dual图示例

定义2. 约束网络N中任意变量V所对应的2V-dual图是指将N对应的2-dual图中所有不包含变量V的结点和边删掉得到的图.

图2中给出了图1中约束网络中变量F对应的2F-dual图，是通过删掉图1中所有不包含F的结点和边后得到的图.下面引入1种能够确保约束网络维持PWC+GAC的极小约束范围S，它是通过将原始约束范围中一些变量删掉后得到新的约束范围.

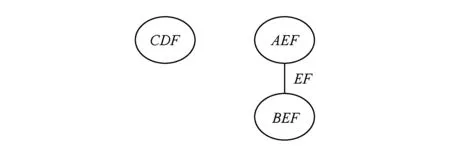
Fig. 2　A 2F-dual graph.图 2　1个2F-dual图示例

定义3. 若新的约束范围S使得在约束网络中的任意变量V所对应2V-dual图的每个连通分量中存在且只存在唯一的约束c使得V∈S[c]，则称S是约束网络的极小约束范围.

图1中约束网络所对应的1个极小约束范围S：S[c1]={A,B,C,D},S[c2]={F},S[c3]={E},S[c4]={B,F},S[c5]={}.

引理1. 对于任意2个相邻约束c1和c2，已知c1中元组在c2上都存在PW支持，∀V∈scp(c1)∩scp(c2)，若V在c1上是GAC的，那么V在c2上也是GAC的.

证明. 不妨设(V，a)在c1上的支持为τ1，τ1,在c2上的PW支持为τ2，因为τ2是τ1在c2上PW支持，所以我们可知τ2和τ1在交集变量上的取值是相等的，而又因为V是c1和c2的交集变量，所以τ1和τ2在V上的值是相等的，故可知τ2是(V，a)在c2上的支持.

证毕.

定理1. 约束网络在对应的2-dual图上维持PWC后，约束网络是GAC的，当且仅当所有约束c的极小约束范围S[c]中的所有变量在c上维持GAC.

证明.

1) 必要性.因为S[c]⊂scp(c)，所以当在scp(c)中的变量都在c上维持GAC后，相应地在S[c]中的变量也都在c上维持GAC.

2) 充分性.若所有约束c的极小约束范围S[c]中的所有变量在c上维持GAC而约束网络不是GAC，则存在(V，a)在约束c上没有支持且变量V不属于S[c]，这时根据定义3可知，存在1个和c在同一连通分量中的约束c1，使得S[c1]包含V，假设c1,c2,…,c是从c1到c的路径，若V在c1上是GAC的，则(V,a)在c1上存在支持τ1.根据引理1可知，(V,a)在c2中必定存在1个支持τ2，以此类推(V,a)在c上也有支持，于是产生矛盾.

证毕.

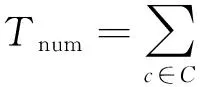
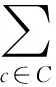
证毕.

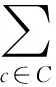
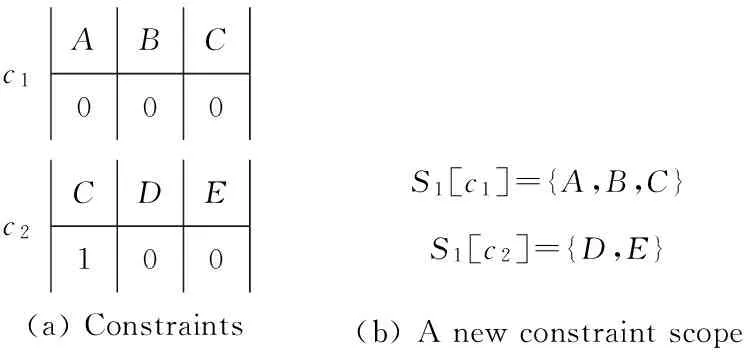
证毕.

Fig. 3A constraint network and a new constraint scope.
图31个约束网络和新约束范围

定理1确保约束网络在极小约束范围上维持PWC+GAC等价于初始约束范围，而定理2和定理3说明极小约束范围就是最小约束范围.

算法3用于求约束网络的极小约束范围S，其主要思想是直接默认变量x保留在对应2x-dual图的各个连通分量中第1个被访问到的约束c的极小约束范围S[c]中，然后通过算法4深度优先搜索确保对应2x-dual图中和c在同一连通分支上的所有其他约束不在极小约束范围S中保留变量x.算法时间复杂度为O(|X|U2)，U表示变量中最大的度(包含某个变量的约束数量)

算法3. 求约束网络N的极小约束范围S.

getS(N)

① begin

② for eachc∈Cdo

③S[c]←∅;

④Mark[c]←-1;

⑤M←∀x∈X;

⑥ end for

⑦ for eachx∈Mdo

⑧ for eachc∈Candx∈scp(c) do

⑨ ifMark[c]≠xthen

⑩Mark[c]←x;

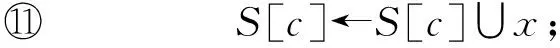
算法4. 遍历和约束c同一连通分支的约束.

searchCoCo(Mark,c,x)

① begin

②stack←{c};

③ whilestack≠∅ do

④cnow←pop(stack);

⑤ for eachc∈Candx∈scp(c′) do

⑥ if|scp(c′)∩scp(cnow)|>1 then

⑦ ifMark[c′]≠xthen

⑧stack←stack∪c′;

⑨Mark[c′]←x;

⑩ end if

例1. 汽车配置问题可以直观的表示为由表约束组成的约束可满足问题，表1中给出了1个关于汽车的简单配置问题，主要考虑环保对配置汽车的2个简单约束:约束1是对不同类型车和发动机类型及其发动机排放标准的限制;约束2是限制一些汽车必须装OBD，约束表中列出所有允许的元组.

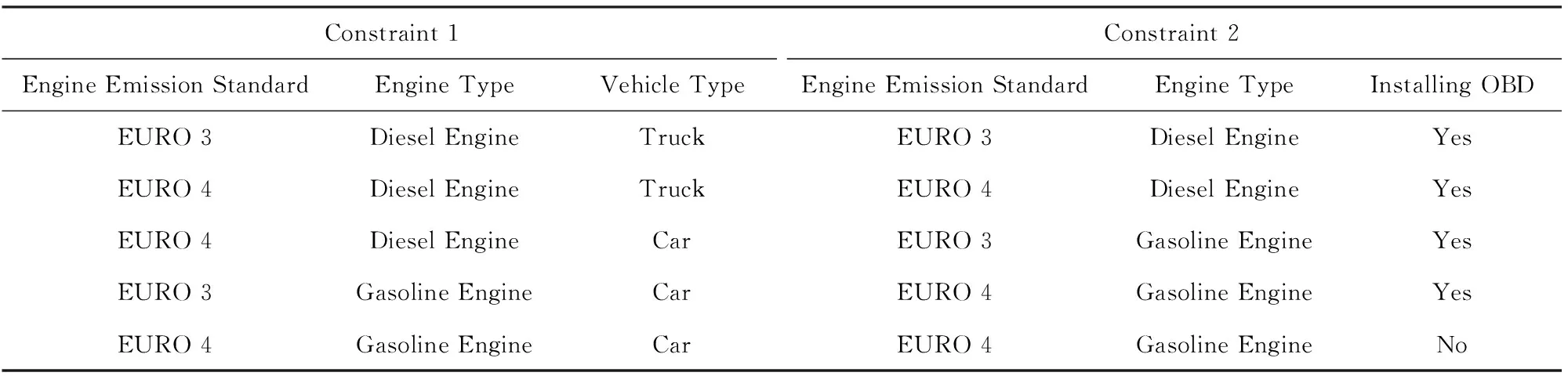
Table 1　A Instance of Car Configuration

通过算法3可以得到例1中约束网络对应的1个极小约束范围是：S[Constraint 1]={Engine Emission Standard，Engine Type，Vehicle Type}，S[Constraint 2]={Installing OBD}.相应在eSTR算法构建了ctr计数器以后，便可以删去不在极小约束范围中的列，表2给出了根据极小约束范围删去表1中汽车配置例子的列后得到的结果.

应用极小约束范围后，在单个约束c上执行1次eSTR的时间复杂度是O(sd+max(s,g)t)，好于初始约束范围的时间复杂度O(rd+max(r,g)t)[17]，其中s=|S[c]|，r=|scp(c)|，g是指约束范围交集中变量数大于1的相邻约束数目，t是当前表中元组数量.但是每次约束检测删去的元组会减少，同时最终维持PWC+GAC要删去的元组是一致的，于是增加了约束的检测次数，总的来说应用极小约束范围可以降低每次约束检测的时间，但会增加约束检测的次数，约束检测是指对约束执行1次eSTR算法.

Table 2　The Result of Deleting Redundant Columns

①http:www.cril.univ-artois.fr～lecoutresoftware.html

②http:www.cril.univ-artois.fr～lecoutrebenchmarks.html

约束网络在极小约束范围上维持GAC时，算法只检测元组在极小约束范围中变量值的有效性，同时由于在eSTR算法初始化时建立了ctr计数器，检测PW支持时也不会访问具体元组中的变量值.于是我们可以通过将元组集中那些不会被访问到的列删去来降低eSTR算法的空间消耗，若约束c拥有独立的元组集，那么极小约束范围S[c]能够减少Ο((r-s)t)的空间消耗.

4实验结果

我们分别在随机问题和benchmark问题上测试优化算法并将其和eSTR2，eSTR2w进行比较，下面采用P和T来分别表示2种不同的优化方式，P表示PWsup数据结构，T表示极小约束范围，另外在实现eSTR算法时，本文是先删去2-dual图中的多余边[13]后才建立的ctr计数器，在本文所测的所有实例上删多余边后eSTR算法基本都比没删多余边要快许多，所以本文的eSTR算法都先删去多余边.在回溯中采用静态变量启发式dominitdeg和字母顺序的值启发式，dominit是变量初始域的大小.大部分实验是在环境1中进行，但是由于Renault和aim问题中存在许多非常简单的实例，在环境1中的运行时间小于1ms，所以我们在环境2中测试这2类问题.

实验环境1. 4.0GB内存、3.40GHz主频、i7处理器、Windows7操作系统和Java语言.

实验环境2. 2.0GB内存、2.27GHz主频、i3处理器、Windows7操作系统和Java语言.

4.1随机问题测试

我们选择随机约束可满足问题模型ModelRB[8]对算法进行测试，具体实例是通过使用RBGenerator2.0①来产生的，ModelRB问题由5个参数控制，r,n,d,e,p中的r是指约束的元数，n是指变量个数，d是变量值域的大小，e是约束的个数，p是约束的紧度(tightness).我们选取r=13,n=60,d=2,e=20的问题进行测试，每个紧度测20个实例.图4展现p在0.8～0.95的实验结果，紧度间隔是0.01，我们只给出0.8～0.95的实验结果是因为在0.8～0.95之外紧度上13,60,2,20,p问题非常容易.eSTR2+P在13,60,2,20,p问题上的CPU运行时间平均比eSTR2快23%，eSTR2+P+T平均比eSTR2+P快10%、比eSTR2快31%，这说明PWsup数据结构和极小约束范围在这类问题上能够提高eSTR2算法的时间效率.删掉dual图中的多余边后，eSTR2比eSTR2w具有更好的时间效率，所以相应的eSTR2+P+T平均要比eSTR2w快37%.另外从图4我们可以知道2种优化方式在13,60,2,20,p问题不同紧度上能够稳定地减少eSTR2算法的CPU运行时间.

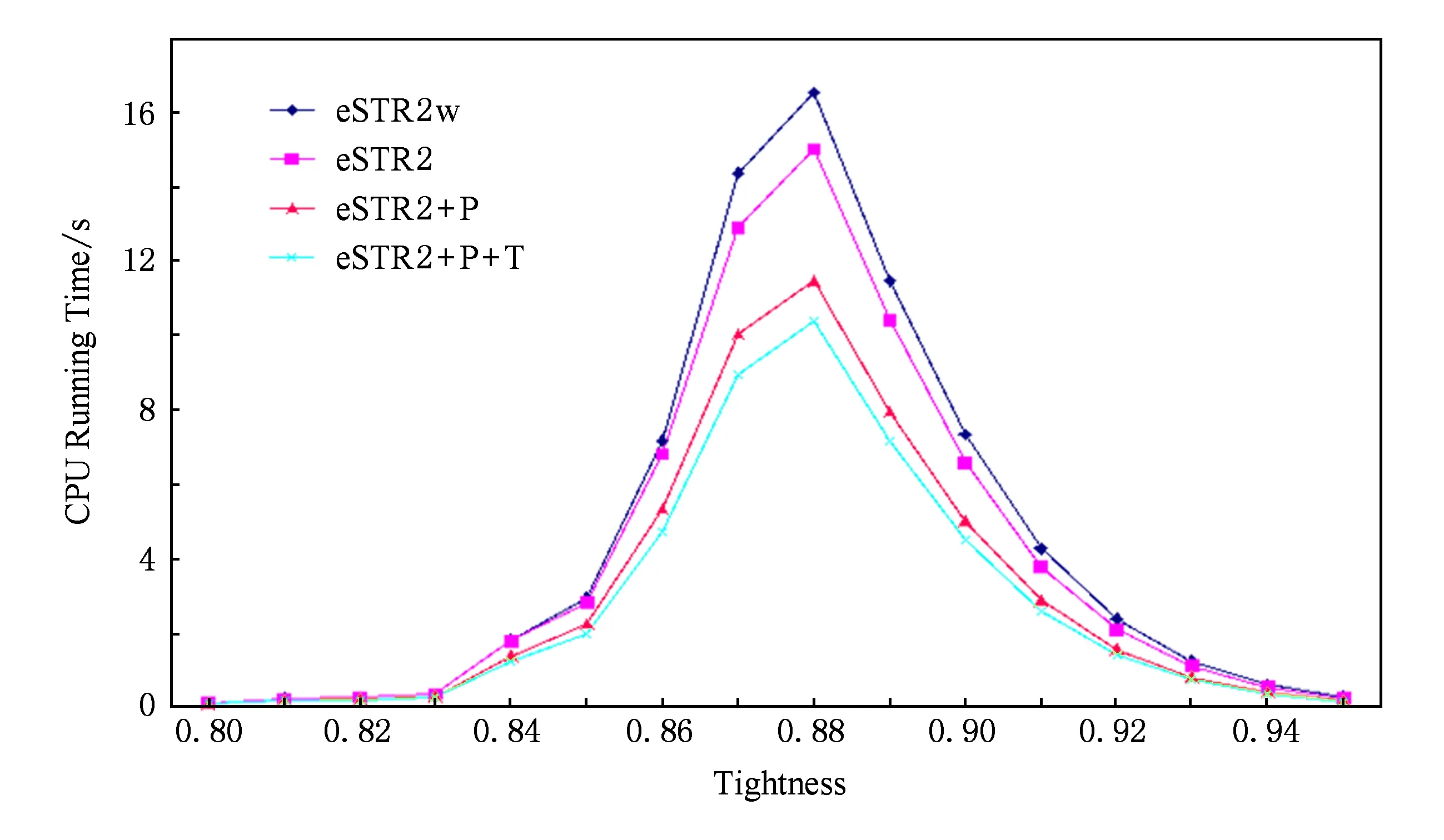
Fig. 4　Experimental results of random instances.图4　随机实验结果

4.2Benchmark测试

本文所测的大部分实例是从Lecoutre的主页②上下载的，另外还有3类实例是使用RBGenerator2.0①来产生的，它们分别是rand-12，rand-5，rand-10问题.

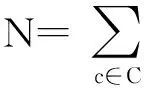
Table3ResultsofDeletingVariablesbyMinimalConstraintScopeS

表3　极小约束范围S删变量结果

表4给出了每个算法在不同问题上的平均CPU运行时间，加粗表示是最好的时间，#Instance表示某类问题包含的实例个数，除了dubois问题外，eSTR2+P+T的CPU平均运行时间一般都比eSTR2要快，其中eSTR2+P+T在mdd-25-7问题上比eSTR2快41%，在rand-8问题上、比eSTR2快37%.删除了dual图中的多余边之后，eSTR2在许多类实例上要比eSTR2w更具有优势；相应地除了MDD-23-15和rand-3问题外,eSTR2+P+T算法的CPU平均运行时间要比eSTR2w快；在MDD-25-7问题上；eSTR2+P+T比eSTR2w快2倍；在rand-8问题上，eSTR2+P+T比eSTR2w快43%.表5列出不同实例的CPU运行时间和扩展结点数，每类问题选2个不同难易程度的实例，比如renault-mod-0实例只扩展了111个结点，而renault-mod-30实例扩展了1 449 414个结点.

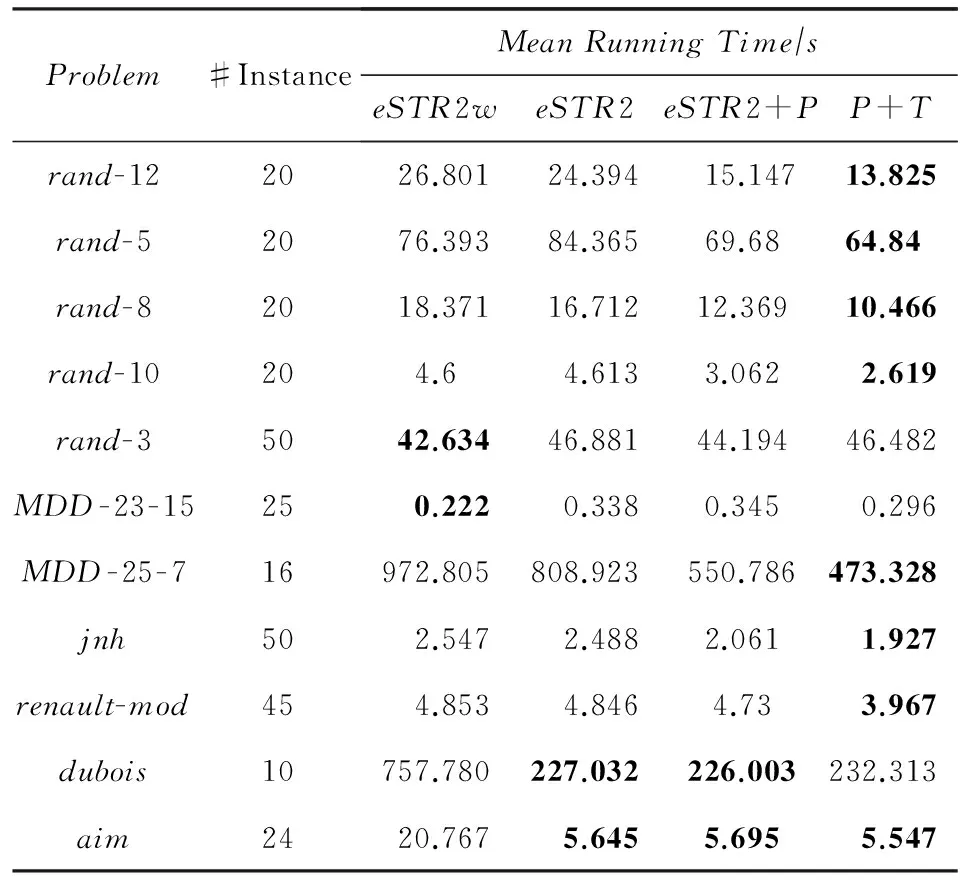
Table 4　Mean Running Time of Different Problem

aim问题的元组集很小，只包含了6个或7个元组，这导致了PWsup数据结构的优化效果不好，因为在元组集很小的时候，算法维持数据结构的额外时间开销所占比例较多;另外aim是三元问题，在低元问题上极小约束范围在每次约束检测所减少的时间比较少，因为STR2本身就能够避免一些变量的有效性检测，而且在低元问题上单个约束的极小约束范围能删去的变量个数较少，所以在低元问题上极小约束范围的时间优化效果不理想.dubois问题只有2对约束的约束范围交集中变量个数大于1同时只删去了3%的约束变量，所以PWsup数据结构和极小约束范围的时间优化效果都不理想.

MDD-23-15问题上PWsup数据结构的优化效果不好是因为算法在该问题上维持PWC时只进行1次约束检测就删空了变量域，显然在这种实例上eSTR2w是最优的.rand-3是1个三元问题，低元问题上极小约束范围减少的约束检测时间较少，无法抵消在三元随机问题上约束检测次数增多带来的时间消耗，所以在这类问题上极小约束范围降低了算法的时间效率.在renault-mod问题上，PWsup数据结构的时间优化效果不好是因为删去dual图中的多余边后只剩下少量的边(约束范围交集中变量个数大于1的约束对)，而在边较少时PWsup的效果并不理想.

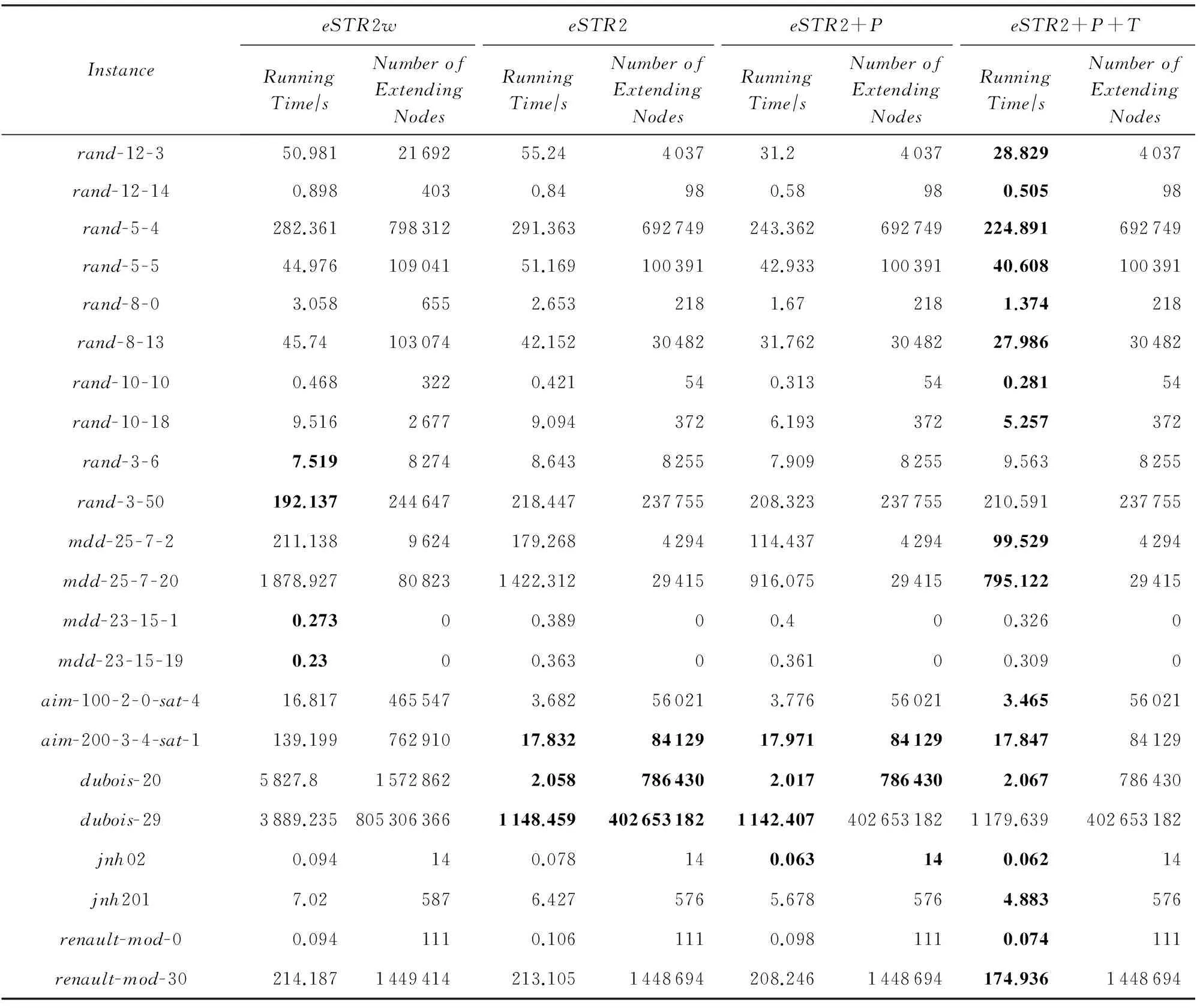
Table 5　The Number of Extending Nodes and Running Time for Some Instances

5总结

本文提出了PWsup数据结构和极小约束范围2种方式来对eSTR算法进行优化，PWsup数据结构在拥有较大元组集且约束范围交集中变量个数大于1的约束对较多的问题上具有非常明显的时间优化效果，而极小约束范围在能删去许多变量且约束拥有独立元组集的问题上，可以减少大量的空间消耗，例如rand-12问题，极小约束范围能够删去元组集中96%的列.将PWsup数据结构和极小约束范围相结合后便能够在许多类问题上减少eSTR2算法的空间消耗并提高时间效率，尤其是在高元问题上，例如在MDD-25-7问题上eSTR2+P+T平均能够减少eSTR2算法41%的CPU运行时间，同时删去了元组集中94%的列.

参考文献

[1]LecoutreC.STR2:Optimizedsimpletabularreductionfortableconstraints[J].Constraints, 2011, 16(4): 341-371

[2]ChengKCK,YapRHC.AnMDD-basedgeneralizedarcconsistencyalgorithmforpositiveandnegativetableconstraintsandsomeglobalconstraints[J].Constraints, 2010, 15(2): 265-304

[3]XiaWei,YapRHC.OptimizingSTRalgorithmswithtuplecompression[C]ProcofPrinciplesandPracticeofConstraintProgramming.Berlin:Springer, 2013: 724-732

[4]KatsirelosG,WalshT.Acompressionalgorithmforlargearityextensionalconstraints[C]ProcofPrinciplesandPracticeofConstraintProgramming.Berlin:Springer, 2007: 379-393

[5]JeffersonC,NightingaleP.Extendingsimpletabularreductionwithshortsupports[C]ProcoftheIntJointConfonArtificialIntelligence.MenloPark,CA:AAAI, 2013: 573-579

[6]LiHongbo,LiangYunchun,GuoJinsong,etal.Makingsimpletabularreductionworksonnegativetableconstraints[C]Procofthe27thAAAIConfonArtificialIntelligence.MenloPark,CA:AAAI, 2013: 1629-1630

[7]XuKe,LiWei.Exactphasetransitionsinrandomconstraintsatisfactionproblems[J].JournalofArtificialIntelligenceResearch, 2000, 12(1): 93-103

[8]XuKe,BoussemartF,HemeryF,etal.Randomconstraintsatisfaction:Easygenerationofhard(satisfiable)instances[J].ArtificialIntelligence, 2007, 171(8): 514-534

[9]LiHongbo,LiZhanshan,WangTao.Improvingcoarse-grainedarcconsistencyalgorithmsinsolvingconstraintsatisfactionproblems[J].JournalofSoftware, 2012, 23(7): 1816-1823 (inChinese)(李宏博, 李占山, 王涛. 改进求解约束满足问题粗粒度弧相容算法[J]. 软件学报, 2012, 23(7): 1816-1823)

[10]LiZhanshan,ZhangQian,ZhangLiang.Constraintsolvingbasedonthenumberofinstantiation[J].JournalofComputerResearchandDevelopment, 2015, 52(5): 1091-1097 (inChinese)(李占山, 张乾, 张良. 基于实例化次数的约束求解方法研究[J]. 计算机研究与发展, 2015, 52(5): 1091-1097)

[11]JiXiaohui,HuangZhuo,ZhangJian.Ontheintegrationofconstraintprogrammingandoptimization[J].ChineseJournalofComputers, 2005, 28(11): 1790-1797 (inChinese)(季晓慧, 黄拙, 张健. 约束求解与优化技术的结合[J]. 计算机学报, 2005, 28(11): 1790-1797)

[12]LuRunming,LiuSheng,ZhangJian.Searchingfordoublyself-orthogonallatinsquares[C]ProcofPrinciplesandPracticeofConstraintProgramming.Berlin:Springer, 2011: 538-545

[13]JanssenP,JégouP,NouguierB,etal.Afilteringprocessforgeneralconstraint-satisfactionproblems:Achievingpairwise-consistencyusinganassociatedbinaryrepresentation[C]ProcofIEEEIntWorkshoponArchitectures,LanguagesandAlgorithmsinToolsforArtificialIntelligence.Piscataway,NJ:IEEE, 1989: 420-427

[14]BessiereC,StergiouK,WalshT.Domainfilteringconsistenciesfornon-binaryconstraints[J].ArtificialIntelligence, 2008, 172(6): 800-822

[15]PaparrizouA,StergiouK.Anefficienthigher-orderconsistencyalgorithmfortableconstraints[C]Procofthe26thAAAIConfonArtificialIntelligence.MenloPark,CA:AAAI, 2012: 535-541

[16]KarakashianS,WoodwardRJ,ReesonC,etal.Afirstpracticalalgorithmforhighlevelsofrelationalconsistency[C]Procofthe24thAAAIConfonArtificialIntelligence.MenloPark,CA:AAAI, 2010: 101-107

[17]LecoutreC,PaparrizouA,StergiouK.ExtendingSTRtoahigher-orderconsistency[C]Procofthe27thAAAIConfonArtificialIntelligence.MenloPark,CA:AAAI, 2013: 576-582

WangRuiwei.bornin1990.Master.Hismainresearchinterestsincludeconstraintprogramming.

LiZhanshan.bornin1966.PhDandProfessor.MemberofChinaComputerFederation.Hismainresearchinterestsincludemodel-baseddiagnosis,machinelearningandconstraintprogramming.

LiHongbo.bornin1985.PhD.Hismainresearchinterestsincludeconstraintprogramming.

收稿日期：2015-04-08；修回日期：2015-08-11

基金项目：国家自然科学基金项目(61170314,61272208)；吉林省自然科学基金项目(20140101200JC)

通信作者：李占山(zslizsli@163.com)

中图法分类号TP18

Optimizing eSTR Algorithm for Solving Constraint Satisfaction Problems

Wang Ruiwei1,3, Li Zhanshan1,2,3, and Li Hongbo1,2

1(KeyLaboratoryofSymbolicComputationandKnowledgeEngineering(JilinUniversity),MinistryofEducation,Changchun130012)2(CollegeofComputerScienceandTechnology,JilinUniversity,Changchun130012)3(CollegeofSoftware,JilinUniversity,Changchun130012)

AbstractTable constraints, i.e., constraints given in extension by listing all allowed (or forbidden) tuples, are very straight forward and easy to understand, which are intensively studied in constraint programming (CP). Because such constraints are presented in many real world applications from areas such as design, databases, configuration and preferences modeling. However, With the growth of number of constraints and number of tuples, the space cost for table constraints and time cost of consistency checking have become key topics. eSTR is an algorithm which extends simple tabular reduction (STR) to higher-order consistency. After in-depth analysis of eSTR algorithm, this paper proposes two kinds of optimized methods for eSTR: PWsup data structure and minimal constraint scope, and then we prove that the constraint network enforce Pair-Wise Consistency and Generalized Arc-Consistency (PWC+GAC) with minimal constraint scope is equivalent to original constraint scope. At the same time, minimal constraint scope can reduce further space cost of eSTR2 algorithm by deleting columns of the tables in constraints, and PWsupdata structure can reduce the CPU running time by avoiding some unnecessary checking of Pair-Wise-support (PW-support), since tuples in table of the constraint may not lose any PW-supports on the tables of other neighbour constraints. The experimental results show that combining our methods with eSTR2 algorithm can obviously outperform eSTR2 and eSTR2w on many instances of different problems, since it reduces the space cost and CPU running time of eSTR algorithm.

Key wordshigher-order consistency; minimal constraint scope; constraint network; PWsupdata structure; PWC+GAC

This work was supported by the National Natural Science Foundation of China (61170314,61272208) and the Natural Science Foundation of Jilin Province of China (20140101200JC).