基于几何扭曲模型的CCD图像扭曲校正残差及分析*1
傅夏青,彭青玉,冯 杰
(1. 暨南大学 计算机科学系,广东 广州 510632;2. 暨南大学 中法天体测量、动力学与空间科学联合实验室,广东 广州 510632)
基于几何扭曲模型的CCD图像扭曲校正残差及分析*1
傅夏青1 ,2,彭青玉1 ,2,冯杰1,2
(1. 暨南大学 计算机科学系,广东 广州510632;2. 暨南大学 中法天体测量、动力学与空间科学联合实验室,广东 广州510632)
摘要:在已知图像几何扭曲模型的基础上,对2013年2月5日使用云南天文台2.4 m望远镜观测近地小行星(99942)Apophis资料中的58幅CCD图像进行了几何扭曲校正,并对校正后的图像测出的星像位置进行了几何扭曲残差分析。结果发现,星像位置X、Y两个方向的几何扭曲残差约在 ± 0.02 pixel内。为了探究影响几何扭曲残差大小的因素,设计了仿真实验。将模拟星像函数经过设定的扭曲函数模型添加几何扭曲,得到受扭曲的星像函数,并对扭曲前后的星像进行几何扭曲残差分析。结果显示,星像的半峰全宽(FWHM)越大,几何扭曲模型的扭曲变化越快,几何扭曲残差越大。
关键词:天体测量;几何扭曲;扭曲校正;仿真
在天文观测中,望远镜光学成像系统经常存在几何扭曲,导致观测得到的天体位置存在几何扭曲误差。如哈勃空间望远镜(Habble Space Telescope, HST)的第二代广域和行星照相机(Wide-Field Planetary Camera, WFPC2)拍摄的CCD图像存在严重的几何扭曲。其非常小视场(WFPC2视场中的宽场仅为80 × 80 arcsec2)的几何扭曲最大可达5 pixel。这种由光学成像系统导致的星像位置移动,就是几何扭曲(Geometric Distortion, GD)。文[1]通过提高线性项的精度提出了一种改正几何扭曲的方案,求解了哈勃空间望远镜的几何扭曲,使得哈勃空间望远镜拍摄的图像在行星相机视场精确到0.02 pixel,在宽场视场精确到0.01 pixel。解决了几何扭曲问题后,哈勃空间望远镜才真正发挥了其作为空间设备在天体测量上的潜能。在地面望远镜CCD成像观测中,也同样存在视场几何扭曲的影响。文[2-6]对地基天文望远镜几何扭曲的求解做了系统的研究,求解了云南天文台2.4 m和1 m望远镜不同滤光片的几何扭曲模型并做了实际应用。本文基于已知的几何扭曲模型改正观测的CCD图像,并对其中产生的星像位置几何扭曲残差进行了仿真研究。
1观测资料和几何扭曲模型
1.1观测资料
本文所采用的图像是2013年2月5日晚使用云南天文台2.4 m望远镜配备的云南暗弱天体光谱及成像仪(Yunnan Faint-Object Spectrog-raph and Camera, YFOSC)B滤光片观测近地小行Apophis所得图像中的58帧。因为云南暗弱天体光谱及成像仪图像的四周有黑框,所以先对原始图像进行适当的裁剪,裁剪后的图像大小为1 900 × 1 900像素。
1.2几何扭曲模型
文[2-3]提出了一种简便有效的测定望远镜CCD视场几何扭曲的新方法,并应用到云南天文台1 m和2.4 m望远镜抖动观测疏散星团所得的图像,求解了图像的几何扭曲模型。经扭曲改正后,视场中星像的定位精度有了明显提高[5-6]。本文使用的几何扭曲模型正是用这种方法求解得到的。
如图1,将大小为1 900 × 1 900像素的图像划分为19 × 19个大小为100 × 100像素的子区域,黑点表示子区域的中心像素点(格点)。图2为求解得到的云南天文台2.4 m望远镜B滤光片的几何扭曲矩阵的部分数值。矩阵大小为19 × 19,其中每一个数值代表对应格点位置的几何扭曲量。对于该几何扭曲模型数值对应的精度,文[2]做了相关研究,结果显示绝大部分几何扭曲量数值对应的标准差小于0.05 pixel,并且各个标准差的分布是相对随机的,与图像坐标没有显著的相关性。图3是将几何扭曲矩阵放大200倍后用矢量方式绘出。从图3可以看到,几何扭曲在图像的上面角落位置比较大。

图1格点
Fig.1Grids

图2 几何扭曲模型的数值矩阵形式

图3 几何扭曲模型的矢量图
2几何扭曲校正

(1)
由已知的几何扭曲矩阵,图像中任意位置处的几何扭曲可由离该位置最近的4个格点的几何扭曲量用双线性插值的方法求出。

图4几何扭曲
Fig.4Geometric distortion
对图像进行扭曲校正的过程如图5。黑点表示一幅图像中不受扭曲的整像素点,受到几何扭曲后偏移到了空心点的位置。如整像素点P(i,j)受到扭曲后移动到P′(x,y),那么用(2)式求出P′的位置。在扭曲图像中插值求出P′位置的灰度值,并赋值给像素P。这样就恢复了P像素点无扭曲的灰度值。对图像中的每一个像素应用此过程,就可以得到一幅扭曲校正后的图像。
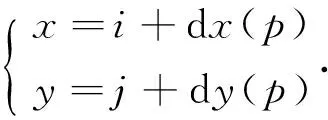
(2)
3实验结果
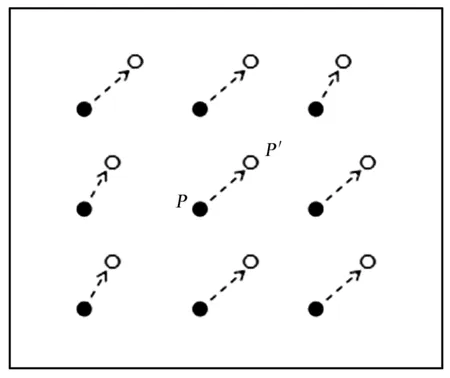
图5像素扭曲示意图
Fig.5Distorted pixel
对观测的CCD图像搜星得到存在几何扭曲的星像坐标,记为B(xgd,ygd)。用(3)式计算其扣除几何扭曲后的星像坐标C(x,y)。式中C的位置未知,其扭曲量也未知,所以无法直接计算C的位置。实际上相邻位置的几何扭曲几乎相等(实际求解的几何扭曲模型最大扭曲量约为±2 pixel)。所以先用B位置的几何扭曲近似C位置的几何扭曲,求出C的近似位置,然后再用迭代的方法计算C更精确的位置。用(4)式将两组坐标相减,得到星像的几何扭曲。图6中灰色点为星像位置的几何扭曲分别随星像位置的x、y坐标的分布情况。
对扭曲校正后的CCD图像搜星得到的星像中心,记为A(xgdc,ygdc),与C(x,y)相减,得到扭曲校正后星像位置的几何扭曲残差,即(5)式。图6中黑色点为星像位置的几何扭曲残差分别随x、y坐标的分布情况。将图6中黑色点表示的几何扭曲残差量程缩小到± 0.05 pixel ,得到图7。图8为星像的几何扭曲残差放大200倍后的矢量分布图。
(5)

图6星像几何扭曲和几何扭曲残差随X/Y的变化
Fig.6The GD errors and residuals inX/Y
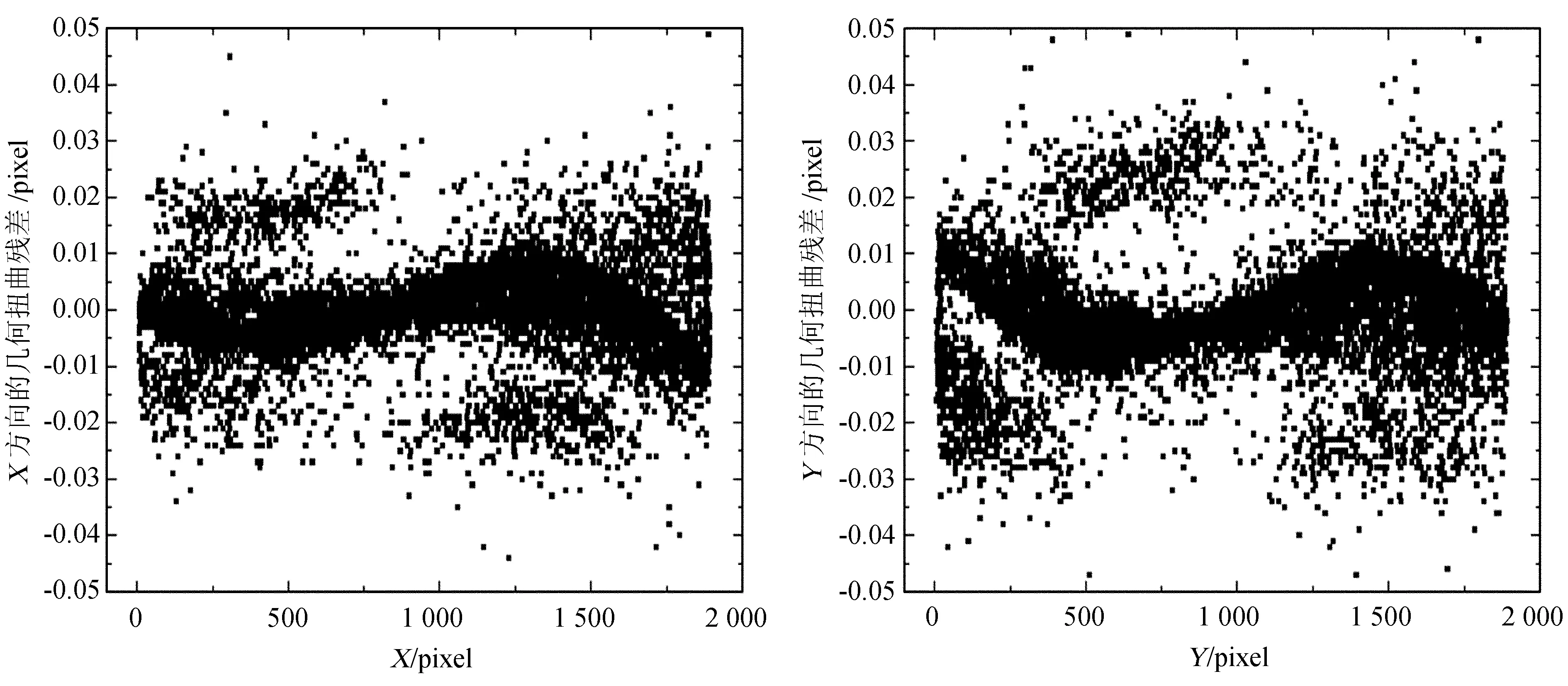
图7几何扭曲残差随X/Y的变化
Fig.7The GD residuals inX/Y
从图6可以看到,图像做扭曲改正前,星像的几何扭曲最大可达1.7 pixel。扭曲改正后,星像的几何扭曲残差基本分布在0附近。从图8可以看到,星像的几何扭曲残差分布的均值为0.008 pixel,标准差为0.009 pixel,并且与图3相比明显消除了几何扭曲的区域系统性。在图7中将残差量程缩小后,可以看到几何扭曲残差大部分在± 0.02 pixel内,但发现几何扭曲残差的分布呈现一定的系统趋势。出现这个现象,可能的一个原因是几何扭曲模型在图像边缘处的变化比较大,造成图像改正后的几何扭曲残差也比较大。为了进一步研究影响几何扭曲残差的因素,本文做了星像几何扭曲的仿真实验。
4仿真实验
4.1仿真实验设计
图8几何扭曲残差矢量图
Fig.8Vectorgraph of GD residuals
如图9,(a)为用一维连续高斯函数模拟的星像f(x),表达式为(6)式,xc是模拟星像的中心。(b)为用正弦函数模拟的扭曲函数模型g(x),表达式为(7)式。图中为了突出星像扭曲的效果,在对扭曲函数绘图时缩小了扭曲函数的周期。实际上,一个星像范围内的扭曲变化非常缓慢。(c)为对模拟星像函数添加泊松噪声,再根据扭曲函数添加扭曲后得到的连续星像函数。根据扭曲前后模拟星像函数的积分面积不变,由(8)式可以推导出受扭曲后的连续星像函数h(t),如(9)式。
根据文[7]对不同星像定心算法的比较和精度分析表明,高斯拟合法是一种精度相对较高的定心算法,且星像分布与高斯函数相似程度越高,则测量精度越高。实际求解的几何扭曲模型最大扭曲量约为2 pixel,扭曲后的星像分布函数非常接近高斯函数。因此采用高斯拟合法对受扭曲后的星像定心。具体地,对受扭曲后的连续星像函数在其± 2.5σ像素范围内采样(σ是高斯函数的标准差)。设此范围内覆盖的像素区间为(i,i+n)。即对(i,i+1)、(i+1,i+2)…(i+n-1,i+n)区间分别积分,结果得到一组离散数据点,用图9(c)中的点表示。对这些离散数据点用(10)式做最小二乘拟合,求出受扭曲后的星像中心xc′。实验中对每个像素区间积分时,采用两点高斯数值积分[8]。
(10)
(6)~(10)式中,B为背景值,实验中设定星像扭曲前后背景值不变;H为星像亮度值;A是扭曲函数幅度,实验中参考真实资料求解得到的扭曲矩阵,将A设为2 pixel;T是扭曲函数的周期,T越小,扭曲变化越快;H′、xc′、σ′ 为对离散点做最小二乘拟合后求得的高斯函数的参数。

图9(a)模拟的星像函数; (b)扭曲函数; (c)扭曲后的星像函数
Fig.9(a) Simulated star profile function; (b) GD function; (c) Distorted star profile function
4.2仿真实验结果
设图像的宽度是1 024 pixel,在[0, 1023]区间内随机生成500个一维模拟星像函数。由(11)式计算几何扭曲残差,实验结果如图9。
(11)
图10中(a)表示设定扭曲函数的周期T=512 pixel,模拟星像的全峰半宽分别为13、9、4 pixel时,几何扭曲残差随星像x坐标的分布情况。表1是它的数值统计。(b)表示设定模拟星像的FWHM=9 pixel,扭曲函数的周期分别为256、512、1 024 pixel时,几何扭曲残差随x坐标的分布情况。表2是它的数值统计。
从图10(a)和表1可以看到,当扭曲函数的周期相同时,星像的全峰半宽越大,几何扭曲残差越大。例如在固定周期T=512 pixel情况下,当FWHM=4 pixel时,几何扭曲残差最大为0.006 pixel,标准差为0.001 86 pixel;当FWHM=9 pixel时,几何扭曲残差最大增至0.01 pixel,标准差增大到0.002 76 pixel;当FWHM=13 pixel时,几何扭曲残差最大值虽然几乎没有增大,但标准差达到了0.004 pixel。从图10(b)和表2可以看到,当星像的全峰半宽相同时,扭曲函数的周期越小,几何扭曲残差越大。例如在固定FWHM=9 pixel情况下,当T=1 024 pixel时,几何扭曲残差最大为0.007 5 pixel;当T=256 pixel时,几何扭曲残差最大达到0.015 8 pixel。也就是说,星像的全峰半宽越大,扭曲函数的周期越小,几何扭曲残差越大。因为星像的全峰半宽越大,扭曲函数的周期越小,都将导致一个星像范围内所包含的扭曲变化越大。从图10还可以看到,几何扭曲残差的变化趋势跟扭曲函数的变化一致。图7中几何扭曲残差的分布在图像的四周比较大,中间部分则较小。对应图3的几何扭曲模型,几何扭曲在图像的角落处变化较快,相当于仿真实验中的扭曲函数的周期T较小的情况;几何扭曲在图像的中间部分变化较小,相当于仿真实验中扭曲函数的周期T较大的情况。从而导致了图7中分布在图像四周的星像几何扭曲残差较大,分布在图像中间的星像几何扭曲残差较小。

图10(a)相同周期下不同全峰半宽的扭曲残差分布; (b)相同全峰半宽下不同周期的扭曲残差分布
Fig.10(a) The GD residuals in the same period but with different FWHM; (b) The GD residuals with the same FWHM but in different periods
表1相同周期不同全峰半宽下扭曲残差数值统计
Table 1The GD residuals statistics in the sameperiod but with different FWHM

FWHM(T=512)/pixelMax/pixelSD/pixel40.00590.0018690.01010.00276130.01030.00400
表2相同全峰半宽不同周期下扭曲残差数值统计
Table 2 The GD residuals statistics in the same FWHM but in different periods

T(FWHM=9)/pixelMax/pixelSD/pixel2560.01580.005645120.00870.0027210240.00750.00262
5结论
在已经求解出几何扭曲模型的情况下,对CCD图像进行几何扭曲校正。校正后,星像位置在X、Y两个方向的几何扭曲残差约在± 0.02 pixel内。对星像位置的几何扭曲残差进行仿真研究,分别测试了星像在相同的扭曲函数周期下不同全峰半宽,以及星像在相同的全峰半宽下不同扭曲函数周期的几何扭曲残差的大小和变化规律。结果发现星像的全峰半宽越大,扭曲函数周期越小即扭曲模型变化越快,星像位置的几何扭曲残差越大。这个结论解释了CCD图像经几何扭曲校正后分布在图像四周的星像其几何扭曲残差较大,而分布在图像中间的星像其几何扭曲残差较小的现象。
参考文献:
[1]Anderson J, King I R. An improved distortion solution for the Hubble Space Telescope′s WFPC2[J]. The Publications of the Astronomical Society of the Pacific, 2003, 115(803): 113-131.
[2]Peng Q Y, Vienne A, Zhang Q F, et al. A convenient solution to geometric distortion and its application to Phoebe′s observations [J]. The Astronomical Journal, 2012, 144(6): 170-179.
[3]Zhang Qingfeng, Peng Qingyu, Zhu Zi. Preliminary results of solving the problem of geometric distortion for the 2.4m telescope at Yunnan Observatory[J]. Research in Astronomy and Astrophysics, 2012, 12(10): 1451-1456.
[4]彭青玉, 涂兵. 求解CCD图像几何扭曲的初步结果[J]. 中国科学: 物理学 力学 天文学, 2011, 41(9): 1126-1130.
Peng Qingyu, Tu Bing. Preliminary results of solving geometric distortions for a CCD image[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2011, 41(9): 1126-1130.
[5]杨纯一, 彭青玉, 张庆丰. 2.4米望远镜天体测量试验[J]. 天文研究与技术——国家天文台台刊, 2013, 10(2): 156-161.
Yang Chunyi, Peng Qingyu, Zhang Qingfeng. An astrometric experiments on the 2.4m telescope of the Yunnan Observatory[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2013, 10(2): 156-161.
[6]Peng Q Y, Wang N, Vienne A, et al. Precise CCD positions of Phoebe in 2011-2014[J]. Monthly Notices of the Royal Astronomical Society, 2015, 449(3): 2638-2642.
[7]李展, 彭青玉, 韩国强. CCD图像数字定心算法的比较[J]. 天文学报, 2009, 50(3): 340-348.
Li Zhan, Peng Qingyu, Hang Guoqiang. Comparison of digital centering algorithms based on CCD images[J]. Acta Astronomical Sinica, 2009, 50(3): 340-348.
[8]施妙根, 顾丽珍. 科学和工程计算基础[M]. 北京: 清华大学出版社, 1999.
*基金项目:国家自然科学基金 (11273014, U1431227) 资助.
收稿日期:2015-09-39;
修订日期:2015-11-23
作者简介:傅夏青,女,硕士. 研究方向:图像处理. Email: cherishfu2015@sina.com
中图分类号:P123.2+2
文献标识码:A
文章编号:1672-7673(2016)03-0382-07
Residuals and Analysis of Geometric Distortion Correction of CCD Images Based on Geometric Distortion Pattern
Fu Xiaqing1,2, Peng Qingyu1,2, Feng Jie1,2
(1. Department of Computer Science, Jinan University, Guangzhou 510632, China, Email: 897533236@qq.com 2. Sino-French Joint Laboratory for Astrometry, Dynamics and Space Science, Jinan University, Guangzhou 510632, China)
Abstract:Fifty eight CCD frames taken by the 2.4m telescope of Yunnan Observatories on Feb 5, 2013 were corrected for their Geometric Distortions (GDs) with the solved GD pattern by the approach proposed in Reference[2]. It is found that the GD residuals of the pixel position of stars still exist about ± 0.02 pixels in both X and Y directions while they are bigger at some corners and smaller in the middle part of each CCD frame. A simulation experiment was then carried out to analyze the cause that affects the GD residuals. Our results show that the GD residuals grow bigger when the FWHM (Full Width at Half Maximum) of a CCD stellar image becomes bigger or the GD pattern changes fast. This experiment can explain the variation of the GD residuals of stars after correcting the GDs.
Key words:Astrometry; Geometric distortion; Distortion correction; Simulation
CN 53-1189/PISSN 1672-7673

