基于相位一致性和方向滤波冕环震荡识别与跟踪*1
冯 松,王 洋,赵 燕,袁 泉,杨云飞,邓 辉,王 锋
(1. 昆明理工大学信息工程与自动化学院计算机系,云南 昆明 650500; 2. 昆明理工大学云南省计算机技术应用重点实验室,云南 昆明 650500)
基于相位一致性和方向滤波冕环震荡识别与跟踪*1
冯松1,2,王洋1,2,赵燕1,2,袁泉1,2,杨云飞1,2,邓辉1,2,王锋1,2
(1. 昆明理工大学信息工程与自动化学院计算机系,云南 昆明650500; 2. 昆明理工大学云南省计算机技术应用重点实验室,云南 昆明650500)
摘要:冕环结构的准确识别和跟踪有利于更好地研究和分析冕环特征以及同耀斑爆发和日冕物质抛射之间的关系。提出基于相位一致性和方向滤波的冕环震荡识别和跟踪方法。识别过程如下:首先,使用相位一致性技术对太阳图像中的冕环特征进行识别;其次,对识别后的图像进行二值化处理;接着使用方向滤波去除非冕环的结构特征;然后,对其进行形态学处理;最后,再对识别结果进行二次曲线拟合。运用所提算法对2011年9月6日由太阳动力学观测站(Solar Dynamics Observatory, SDO)在Fe IX 17.1 nm波段观测到的冕环震荡进行了识别和跟踪,结果验证了所提算法的可行性和准确性。证明所提算法能被用于冕环特性以及震荡过程的研究和分析。
关键词:相位一致性;方向滤波;冕环震荡;震荡周期
日冕位于太阳大气的最外层,在上面可以观测到一些亮的环形结构,它们被称为冕环。冕环由日冕磁场束缚的热等离子体发亮而形成环状结构,是太阳磁场结构的一种表现形式。它们同日冕物质抛射、太阳耀斑、太阳风暴等有密切的关系[1]。研究冕环及其演化过程对于理解太阳大气层的磁场活动和预报太阳风暴具有重要意义。
太阳耀斑爆发和日冕物质抛射释放的大量能量引起附近局部磁场结构的急剧变化,导致附近的冕环结构产生震荡[2-4]。这些震荡不仅仅发生在一条冕环结构上,也同时出现在多条冕环结构上。最近的研究表明,这种震荡是驻波的一种表现形式,但是每个环上由于震荡的频率、相位以及衰减系数的不同,往往呈现不同的震荡特征[5-9]。研究这些特征对于更好地理解耀斑爆发和日冕物质抛射对日冕磁场的影响具有很大的帮助。
然而准确地识别和提取冕环特征结构面临非常大的困难。这是由于:(1)冕环是由日冕磁场束缚的热等离子体形成,这些等离子体分布并不均匀,虽然冕环结构的强度较大,但强度变化(梯度)较小,导致冕环结构的边缘模糊,造成提取困难;(2)各个冕环之间的距离较近而且相互交错,导致产生的二维图像环形结构彼此交叉重叠;(3)由于磁场活动的复杂性导致了冕环结构呈现多种形态,如环形结构出现断裂等问题;(4)在冕环附近还存在非环形的太阳特征,如海绵状亮斑,这些都增加了冕环提取的复杂性和准确性。
目前冕环的识别方法主要分为两类[10-13]:一类是运用图像空间域的强度和梯度阈值对特征结构进行识别和提取;另一类是利用频域或小波域对不同的频率特征进行滤波,识别和提取冕环特征。广义上讲,图像的结构特征,如特征边缘、尺度和纹理等大量底层信息存储在图像的相位谱中。文[14-15]证明了相位一致性在表征特征结构时对强度、对比度、照度具有不变性,而且通过计算图像的局部能量实现了对图像特征的稳定提取。目前,相位一致性技术已经应用于黑子本影亮点和本影耀斑以及光球米粒等低对比度太阳图像特征的提取和识别[16-19]。
本文运用相位一致性技术并结合方向滤波的方法对一个由太阳动力学观测站搭载的太阳大气成像仪(Atmospheric Imaging Assembly, AIA)[20]在2011年9月6日由谱线Fe IX 17.1 nm波段观测到的冕环震荡进行识别和分析,并同已有的文献结果进行比较来检验所提方法的可行性和准确性。
论文首先介绍所用的实验数据,其次简述冕环震荡的识别过程,然后对识别的冕环震荡进行统计分析,并同已有文献结果作比较,最后对本文进行总结。
1实验数据
选择震荡事件发生在编号为11283的活动区为实验数据,时间从2011年9月6日22时17分到2011年9月6日22时34分。观测资料由太阳大气成像仪在谱线Fe IX 17.1 nm波段记录。冕环震荡由一个附近爆发的X2.1级耀斑引起。该组数据共包含65幅图像,间隔时间为12 s,图像的像元分辨率是0.6″。图1(a)展示了2011年9月6日22时17分获得的图像,其中白色箭头所示的位置为耀斑爆发的位置,它引起了图1(a)中白色方框标记区(即图1(b))冕环产生了震荡。图1(b)展示了这个区域的细节。它的大小为210 × 144″。在图1(b)中,由数字1和2指示的位置为耀斑爆发能量释放所产生的图像结构特征,它导致了附近的冕环产生剧烈震荡,尤其是箭头LoopA和LoopB指示的两个冕环结构震荡尤为明显。为了同文[9]做比较,本文主要针对冕环A和冕环B的震荡运用所提算法进行识别和跟踪,并对其结果进行统计分析来检验算法的可行性和准确性。
图1冕环
Fig.1Loops
2识别和跟踪方法
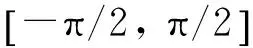
从图2(b)可以看出,那些海绵状亮斑和由于耀斑爆发产生的近似垂直的一些特征(如图中上方中间位置被白色方框标记)干扰冕环A和B的提取。所要识别和提取的冕环A和冕环B方向近似水平。因此算法选用方向滤波思想识别近似垂直的特征并去除。算法选用sobel边缘检测算子g(g=[1, 0, -1; 2, 0, -2; 1, 0, -1])作为方向滤波算子检测干扰线段的垂直边缘并去除它们,处理结果如图2(c)。
从图2(c)可以发现,那些近似垂直的干扰特征通过使用方向滤波的方式已经被很准确地去除。然而所需提取的冕环结构仍然存在不连续以及冕环上存在小的孔洞且边缘不规则、噪声点大和冕环粗细不均匀等问题。算法采用形态学的去除小面积、填充、膨胀、闭运算、细化等一系列操作对上述问题进行处理,处理结果如图2(d)。
从图2(d)箭头处可以看出,识别的冕环结构不光滑,存在许多分支结构,并且图中除了所要识别的冕环A和冕环B外,还有一些短的非目标线。因此算法根据节点处各分枝的长短,保留最长的分枝结构,去除短的分枝杂点,并根据环的长度,提取了冕环A和冕环B,结果如图2(e)。
最后对所识别的65幅图像中的冕环A和冕环B进行了二次方程的曲线拟合,获取一个光滑的弧线,其二次方程定义如下:
y=ax2+bx+c,
(1)
其中,x为图像中冕环的横坐标;y为图像中冕环的纵坐标;a、b、c为参数。图2(e)中冕环A和冕环B二次拟合参数a、b、c的值如表1。图2(e)环的拟合结果被叠加到原图上并显示在图2(f)中。由于冕环震荡导致每一幅图像中冕环A和冕环B的形态均不相同,因此本文分别对其进行了逐一拟合,其它的拟合参数并未在此列出,这些拟合线为本文要进行统计分析的特征。
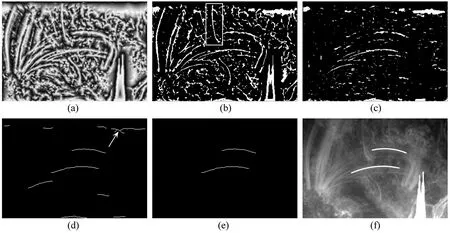
图2识别过程
Fig.2The process of Identification
3实验结果与分析
为了验证所识别冕环的结果,分别选取冕环A和冕环B上在X轴方向上10个位置,然后根据每幅图的二次拟合方程(1)得到Y值,并对这10个Y值分别取它们在每1幅图像上的均值作为这一幅图像冕环震荡的位置。图3(a)和(b)中星号标记的位置即为冕环A和冕环B的Y均值位置随时间T的变化情况。在图3中,横轴表示时间(单位为分钟),纵轴表示冕环移动距离(单位为千米)。从图中可以看出这些星号呈现一个类似衰减的正弦函数,因此采用如下函数拟合这些位移,具体的衰减正弦拟合函数定义如下:

表1 对图1(b)中冕环A和B的二次拟合参数
(2)
其中,A为振幅;τ为衰减时间;t为时间(单位为分钟);T为周期;φ是初相位(单位为度)。

图3 震荡
对于这两个曲线的震荡周期,是采用傅里叶变换的频率分析方法获得。这两个振荡信号的频谱分析图如图4。依据傅里叶频谱分析,这两个环的震荡频率约为8.4 MHz,周期为118 s。运用这个周期值T(即118 s)和拟合方程(2)拟合图3中的星号位置。拟合的曲线如图3(a)和(b),它们的衰减系数约为122 s,但两个震荡序列的相位差近似41°,冕环B先于冕环A,而且B环的振幅也高于A环。这表明由耀斑所引起的冕环震荡不是从最近位置的冕环震荡开始,而是导致较远位置的冕环首先震荡。不过这种位置的远近也可能是由成像的视角导致的。这个分析结果同文[9]的结论一致,进一步验证了本文所提的方法可以运用于冕环特征的研究和分析。

图4频谱分析图
Fig.4Spectrum analysis diagram
4讨论与总结
大多数的冕环震荡是由附近的耀斑爆发和日冕物质抛射引起的,对这些冕环的震荡进行分析可以更好地理解冕环的磁场特征与太阳耀斑爆发和日冕物质抛射的能量释放之间的关系,准确地识别和提取冕环特征至关重要。
本文运用相位一致性和方向滤波的方法分析了一个由太阳大气成像仪在17.1 nm波段观测到的冕环震荡。然而,由于冕环结构的复杂性,本文仅选取了震荡区域中两个比较明显的冕环结构运用相位一致性和方向滤波的图像特征提取方法识别和追踪它们,并根据识别和追踪的结果对这两条冕环的周期、相位差以及衰减系数进行统计分析,并同已有文献的结果进行比较,证明算法可行,识别结果准确。
尽管相位一致性可以很好地解决低信噪比条件下图像特征提取的问题,但由于冕环特征存在于复杂的背景之中以及冕环结构边缘模糊和信噪比低等因素,使得提取的冕环结构不太完整,一些比较细、暗的冕环结构未能识别成功。对于这些情况仅仅从图像处理的角度识别和提取是不够的,需要结合其他波段的数据及磁场反演等物理过程分析,提高冕环识别的准确性,这也是下一阶段研究工作的重点。
参考文献:
[1]Vaiana G S, Rosner R. Recent advances in coronal physics[J]. Annual Review of Astronomy and Astrophysics, 1978, 16: 393-428.
[2]Aschwanden M J. The 3D geometry, motion, and hydrodynamic aspects of oscillating coronal loops[J]. Space Science Reviews, 2009, 149(1-4): 31-64.
[3]White R S, Verwichte E. Transverse coronal loop oscillations seen in unprecedented detail by AIA/SDO[J]. Astronomy & Astrophysics, 2012, 537: A49-A58.
[4]Wang T J, Ofman L, Davila J M, et al. Growing transverse oscillations of a multistranded loop observed by SDO/AIA[J]. The Astrophysical Journal Letters, 2012, 751(2): L27-L32.
[5]Aschwanden M J, Fletcher L, Schrijver C J, et al. Coronal loop oscillations observed with the transition region and coronal explorer[J]. The Astrophysical Journal, 1999, 520(2): 880-894.
[6]Luna M, Terradas J, Oliver R, et al. Transverse oscillations of two coronal loops[J]. The Astrophysical Journal, 2008, 676(1): 717-727.
[7]Luna M, Terradas J, Oliver R, et al. Transverse oscillations of a multi-stranded loop[J]. The Astrophysical Journal, 2010, 716(2): 1371-1380.
[8]Terradas J, Arregui I, Oliver R, et al. Resonant absorption in complicated plasma configurations: applications to multistranded coronal loop oscillations[J]. The Astrophysical Journal, 2008, 679(2): 1611-1620.
[9]Jain R, Maurya1 R A, Hindman B W. Fundamental-mode oscillations of two coronal loops within a solar magnetic arcade[J]. The Astrophysical Journal Letters, 2015, 804(1): L19-L27.
[10]Lee J K, Newman T S, Gary G A. Oriented connectivity-based method for segmenting solar loops[J]. Pattern Recognition, 2006, 39(2): 246-259.
[11]Carcedo L, Brown D S, Hood A W, et al. A quantitative method to optimise magnetic field line fitting of observed coronal loops[J]. Solar Physics, 2003, 218(1): 29-40.
[12]Steger C. An unbiased detector of curvilinear structures[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1998, 20(2): 113-125.
[13]James McAteer R T, Kestener P, Arneodo A, et al. Automated detection of coronal loops using a wavelet transform modulus maxima method [J]. Solar Physics, 2010, 262(2): 387-397.
[14]Kovesi P. Image features from phase congruency[J]. Journal of Computer Vision Research, 1999, 1(3): 1-27.
[15]Kovesi P. Phase congruency: a low-level image invariant[J]. Psychological Research, 2000, 64(2): 136-148.
[16]Feng Song, Xu Zhi, Wang Feng, et al. Automated detection of low-contrast solar features using the phase-congruency algorithm[J]. Solar Physics, 2014, 289(10): 3985-3994.
[17]Feng Song, Yu Lan, Yang Yunfei, et al. Identification of emission sources of umbral flashes using phase congruency[J].Research in Astronomy and Astrophysics, 2014, 14(8): 1001-1010.
[18]Feng Song, Zhao Yan, Yang Yunfei, et al. Identifying and tracking of peripheral and central umbral dots[J].Solar Physics, 2015, 290(4): 1119-1133.
[19]韩翠翠, 蒋霞, 杨云飞, 等. 基于NVST观测的米粒识别和形态特征分析[J]. 科学通报, 2016, 61(8): 881-890.
Han Cuicui, Jiang Xia, Yang Yunfei, et al. Identification and morphology analysis of granules using the New Vacuum Solar Telephone Observations[J]. Chinese Science Bulletin, 2016, 61(8): 881-890.
[20]Lemen J R, Title A M, Akin D J, et al. The Atmospheric Imaging Assembly (AIA) on the Solar Dynamics Observatory (SDO) [M]// The solar dynamics observatory. New York: Springer US, 2012: 17-40.
*基金项目:国家自然科学基金 (U1531132, 11463003, 11573012, 11303011) 资助.
收稿日期:2015-09-01;
修订日期:2015-10-11
作者简介:冯松,男,副教授. 研究方向:天文技术,数字图像处理. Email: ynkmfs@escience.cn
中图分类号:TP391.41
文献标识码:A
文章编号:1672-7673(2016)03-0345-06
Identification and Tracking of Coronal Loop Oscillation Using Phase Congruency and Directional Filter
Feng Song1,2, Wang Yang1,2, Zhao Yan1,2, Yuan Quan1,2, Yang Yunfei1,2, Deng Hui1,2, Wang Feng1,2
(1. Faculty of Information Engineering and Automation, Kunming University of Science and Technology, Kunming 650500, China; 2. Computer Technology Application Key Laboratory of Yunnan Province, Kunming University of Science and Technology, Kunming 650500, China, Email: ynkmfs@escience.cn)
Abstract:Solar flares occurring usually cause oscillations of nearby coronal loops. A precondition of studying these oscillations is to explore how to identify coronal loops. Meanwhile, accurate identification is also crucial to study and analyze the statistical features of the coronal loops and the relationship to coronal magnetic field. However, the traditional identification methods based on intensity and/or gradient threshold have some limitations, because coronal loops hold a relatively low contrast, blurred boundary, and the image noise is close to coronal loops. So we propose a new method to identify coronal loops using phase congruency and directional filter. The identification procedures are as follows: firstly, phase congruency technique is used to identify linear shape in a coronal image; secondly, a binary image is obtained from the image of phase congruency for detecting the loop features; thirdly, a directional filter based on Sobel Operator is applied to remove the redundant features that are nearly perpendicular to those target loops; fourthly, morphological filters are used to extract the shape of those loops; finally, quadratic fitting is used to smooth the identified loop features. For illustrating the performance of the method, the coronal loop oscillations taken with the Atmospheric Imaging Assembly on aboard the Solar Dynamic Observatory on September 11, 2011 are used to evaluate the identification and tracking process. The coronal loop oscillations were caused by a nearby X2.1 flare emission. We analyzed the identified results, and calculated their oscillation period, phase difference and decay coefficient. They are in good agreement with those of previous works. This implies that the proposed method can accurately identify the shape of a loop in an image; furthermore, the results can also be used to study the physical properties of coronal loop oscillations and the relationship to others solar phenomena.
Key words:Phase congruency; Directional filter; Coronal loop oscillation; Oscillation period
CN 53-1189/PISSN 1672-7673

