活性粉末混凝土梁斜裂缝宽度影响参数探析
金凌志,温 晴
(广西岩土力学与工程重点实验室, 桂林理工大学,广西桂林 541004)
活性粉末混凝土梁斜裂缝宽度影响参数探析
金凌志,温晴
(广西岩土力学与工程重点实验室, 桂林理工大学,广西桂林541004)
摘要:为了分析剪跨比、配箍率、钢纤维体积率和纵筋率等不同参数对试验梁斜裂缝宽度的影响,进行4组11根HRB500级钢筋活性粉末混凝土简支梁的抗剪试验研究,并提出其最大斜裂缝宽度计算的建议公式。研究结果表明: 剪跨比、钢纤维体积率、配箍率和纵筋率都对试验梁的斜裂缝宽度有一定的影响,剪跨比越小,试验梁的斜裂缝宽度越小;配箍率、钢纤维含量和纵筋率越大,试验梁的斜裂缝宽度越小;其中钢纤维体积率的影响最为明显。基于普通钢筋混凝土梁斜裂缝宽度计算公式构建的修正公式,可为HRB500级钢筋活性粉末混凝土简支梁的抗剪计算提供些许参考。
关键词:HRB500;活性粉末混凝土梁;影响参数;斜裂缝宽度
活性粉末混凝土[1-4](简称RPC,Reactive Powder Concrete),由20世纪末法国科学家[5]研制出来,通过组成材料的去粗骨料、细度和活性性能,以强度高、韧性强、耐久性高和耐高温性好等优越性能,引起国内外学者的高度重视。美国联邦高速公路管理局(FHWA)[6]测试了1根24 m长的预应力RPC梁的力学性能,表现出了良好的力学性能和变形能力。北京工业大学邓宗才等[7]通过6根T形梁的抗剪试验,将试验值与压力场理论值进行了比较,并对压力场理论进行了改进。徐海兵、邓宗才等[8]还根据剪跨比、配箍率、预应力水平3种参数变化,进行9根超高性能纤维混凝土梁抗剪性能试验,研究表明,抗剪承载力随剪跨比的增大而减小,随预加力、配箍率的增大而增大。金凌志、何培[9]等对4根不同强度等级纵筋和箍筋率的RPC简支梁进行抗剪试验,得出箍筋率对高强钢筋RPC简支梁斜裂缝宽度的影响比较明显,并导致试验梁发生不同形态破坏的结论。此外,北京交通大学、湖南大学等许多高校都对RPC材料及抗剪梁进行了大量相关研究[10-11]。但是有关多参数对高强钢筋RPC简支梁最大斜裂缝宽度的系统研究目前还比较少见,本文通过4组11根不同参数的高强钢筋RPC简支梁的抗剪试验研究,比对分析剪跨比、钢纤维体积率、配箍率和配筋率等不同参数对试验梁最大斜裂缝宽度的影响程度,并提出了高强钢筋RPC简支梁的斜裂缝宽度计算的建议公式,为高强钢筋RPC构件的抗剪设计提供参考。
1试验概况
试验共设计了4组11根试验梁,立方体抗压强度fcu=127 MPa,轴心抗压强度fc=117 MPa,立方体劈裂强度fts=9.19 MPa,钢纤维采用平直钢纤维,直径为0.15~0.2 mm,长径比65~87,抗拉强度>2 000 MPa。梁截面尺寸均为b×h=150 mm×250 mm,L=2 200 mm,主要参数为剪跨比(1.5、2.2、3.0)、箍筋率(0.17%、0.25%、0.58%)、配筋率(4.43%、6.39%、8.04%)、钢纤维体积率(0%、1%、2%、3%)等,详见图1和表1。为确保简支梁受剪先于受弯破坏,根据计算布置了足够的纵向钢筋。

图1 试验梁详图(单位:mm)

试件编号剪跨比(λ)箍筋等级间距配箍率(ρsv)/%纵筋纵筋率(ρ)/%钢纤维含量(vf)/%Vcr/kNVu/kN破坏形态L11.51ϕ6@45004ϕ256.582101.0656.0斜压破坏L22.20ϕ6@45004ϕ256.582220.0356.0剪压破坏L33.02ϕ6@45004ϕ256.582120.0335.0主要斜拉破坏L42.20ϕ6@2250.174ϕ256.582100.7419.3剪压破坏L52.20ϕ6@1500.254ϕ256.582100.3430.9剪压破坏L62.20ϕ6@650.584ϕ256.582100.3426.3弯曲破坏L72.20ϕ6@45004ϕ254.432140.8300.0剪压破坏L82.20ϕ6@45004ϕ258.042221.8425.0剪压破坏L92.20ϕ6@45004ϕ256.58081.7116.0斜拉破坏L102.20ϕ6@45004ϕ256.581151.5249.0剪压破坏L112.20ϕ6@45004ϕ256.583251.4415.0剪压破坏
注:Vcr为试件斜裂缝出现时的剪力值;Vu为试件斜截面破坏时的剪力值。
试验采用门式反力架静力加载方案,加载方式为两点对称集中加载。加载设备采用量程为1 500 kN的液压千斤顶加载系统,主要由储油箱、高压油泵、液压加载器、测力装置和阀门等配件,通过高压油管连接而成, 试验现场照片见图2。

图2 RPC试验梁加载装置
2斜裂缝宽度主要影响因素分析
2.1破坏形态
试验梁L1~L3都是无腹筋梁,L1的剪跨比为1.51,承载力达656 kN,Vu/Vcr=6.5,在支座与加载点之间呈现多条近似平行的斜裂缝,最后斜裂缝形成“短柱”被压碎。L2的剪跨比为2.2比较适中,Vu/Vcr=1.62,剪跨区微裂缝不多,临近破坏时其中一条斜裂缝发展成临界裂缝,发生剪切破坏,外观上与普通混凝土梁的剪压破坏相差不大,但试验梁在丧失承载能力时,剪压区RPC并未出现明显被压碎的现象。L3虽然剪跨比λ≈3,其破坏外观和普通混凝土梁的斜拉破坏外观类似,有斜拉破坏的趋势,但Vu/Vcr=2.8,斜裂缝出现后,并没有很快形成临界斜裂缝,斜裂缝倾角明显小于斜压和剪切破坏的梁。L6因为箍筋比较多,抗剪能力大于抗弯能力,发生了弯曲破坏。L9未掺钢纤维,没有桥架作用,其开裂剪力和极限承载力明显小于其他梁,当荷载加至232.5 kN时,突然发出“蹦”的一声,试验梁宣告破坏,最终形成1条宽度达3.4 mm的斜裂缝,前后贯通,试验梁被劈裂成两部分,也呈现出斜拉破坏的倾向。其余试验梁的剪跨比均为2.2,基本发生剪压破坏。
2.2剪跨比
将剪跨比λ为1.51(L1)、2.26(L2)及3.01(L3)的3根试验梁进行比对分析,由图3可以看出,不同剪跨比的RPC简支梁,初始裂缝宽度基本变化不大,原因可能是钢纤维在RPC内部起到桥架作用,有效抑制了斜裂缝的开展。随着加载值的增长,钢纤维逐渐被拔出,剪跨比的影响才体现出来,随着荷载的增加,剪跨比对RPC梁斜裂缝宽度和倾角的影响越来越明显。剪跨比较小时,RPC梁剪跨区的拉应力比较小,斜裂缝宽度的发展缓慢,最终宽度较小,倾角较大。剪跨比增大,剪跨区的拉应力增加,斜裂缝宽度发展加快,最终宽度也较大,但其倾角减小。

图3 不同剪跨比荷载-最大斜裂缝宽度曲线

图4 不同配箍率荷载-最大斜裂缝宽度曲线
2.3配箍率
本试验共设计4根不同配箍率梁,将梁L2、梁L4、梁L5、梁L6的4根试验梁进行对比分析,由图4可知,配箍率对斜裂缝的出现影响甚微,但可有效抑制斜裂缝的发展。同级荷载下,斜裂缝宽度随配箍率的增加而减小,有腹筋梁L4、L5的最大斜裂缝宽度分别比无腹筋梁L2降低48.6%、42.8%,反映出HRB400级高强箍筋对斜裂缝的抑制作用显著。但是由于L6发生了弯曲破坏,挠度增大,延性比较好,在试验加载过程中,斜裂缝宽度变化不大,突变性不明显。
2.4钢纤维体积率

图5 不同钢纤维体积率荷载-最大斜裂缝宽度曲线
将钢纤维体积掺量为0% (L9)、1%(L10)、2%(L2)、3%(L11)的4根试验梁进行比对分析,如图5所示,掺入钢纤维的梁,开裂荷载明显大于无钢纤维梁,钢纤维体积掺量越高,开裂荷载越大。在开裂荷载后的一段时间内,斜裂缝宽度一直呈线性缓慢增长,随着钢纤维体积率的增加,曲线斜率变小。钢纤维3%掺量与2%掺量的试验梁的曲线平缓段类似,表明在钢纤维体积含量达到2%以后,如果继续增加钢纤维含量,限制裂缝开展的能力并没有得到很明显的改善,但梁的最终斜裂缝宽度会随着钢纤维含量的增加而减小。
2.5纵筋率
将纵筋配筋率为4.43% (L7)、6.58%(L2)、8.04%(L8)的3根试验梁进行比对分析,如图6所示,随着加载的持续,试验梁的配筋率越大,斜裂缝宽度越小。这是因为:一方面高强度的纵向钢筋本身具有较强的销栓作用,能改善试验梁的受剪性能,使RPC的抗剪承载力得以提高;另一方面,高强度的HRB500级纵筋与高性能的RPC良好的协同工作能力,使二者的粘结性能比较好,RPC的受压区截面高度较大,可以减缓和抑制斜裂缝的开展。

图6 纵筋配筋率荷载-最大斜裂缝宽度曲线
2.6各参数影响程度
将试验梁斜裂缝宽度0.3 mm和1.5 mm及其对应的荷载值绘制成图7斜裂缝宽度-荷载曲线,不难发现:不同钢纤维体积掺量曲线跳跃最大,钢纤维掺量越高,同等斜裂缝宽度下梁的对应承载力越高,说明钢纤维体积掺量的变化对斜裂缝宽度的影响最大,这与文献[12]所指出的,初裂荷载随钢纤维体积率的增加而提高,当钢纤维体积率为2%时可提高80%以上,钢纤维体积率越高,最大斜裂缝宽度越小,细次裂缝越多等的结论一致。剪跨比的影响仅次于钢纤维体积含量的变化,剪跨比越小,同等斜裂缝宽度下梁的承载力越高。以配箍率和纵筋率为参数的试验梁,斜裂缝宽度0.3 mm和1.5 mm对应的梁承载力基本在800 kN上下波动,变化幅度并不明显,纵筋率变化的影响相对更小。值得注意的是,箍筋率较高的L6发生弯曲破坏,斜裂缝宽度和长度都很小。因此可以认为,各参数对试验梁斜裂缝宽度的影响程度大小依次为νf>λ>ρsv>ρs。

图7 不同参数斜裂缝宽度-荷载曲线
3有腹筋梁斜裂缝宽度计算分析
3.1斜裂缝宽度计算模型
钢筋混凝土有腹筋梁的抗剪计算模式如图8所示,主要由剪压区RPC剪力Vc、箍筋剪力Vsv、裂缝处骨料咬合力Vra、纵筋销栓力Vd和钢纤维拉力Vs所组成。

图8 钢筋混凝土梁抗剪计算模式
极限剪力
(1)
3.2斜裂缝宽度计算公式
基于上述计算模型,有关钢筋混凝土构件的斜截面裂缝宽度,国内外学者给出了许多计算方法,其中大连理工大学赵国藩教授提出[13]
(2)
(3)
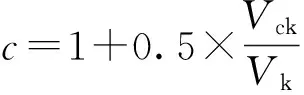
Vck——长期或多次重复荷载作用的剪力;
V——全部荷载的剪力;
σsv——箍筋应力;
λ——剪跨比,1.5≤λ≤3;当λ≥3时,λ=3;当λ≤1.5时,λ=1.5;均布荷载时,λ=1.5;
ftk——混凝土抗拉强度标准值;
μ——纵筋配筋率;
μsv——箍筋配筋率。
3.3计算值与试验值比对
将本文3根梁及新做4根梁和文献[9]的5根有腹筋梁试验数据代入式(2)、式(3),得到表2的计算结果,并与试验值进行对比分析。表2中,Vu为试验剪力极限值;ft为轴心抗拉强度,由劈裂强度换算而得,关系换算式[14]为ft=0.921(1-0.27λf)fts;ωmax为计算最大斜裂缝宽度;ωu为试验观测所得最大斜裂缝宽度。

表2 最大斜裂缝宽度计算值与试验值
对比表2的数据,计算值与理论值的差别比较明显,说明式(2)不太适应于高强钢筋活性粉末混凝土梁斜裂缝宽度的计算,从现场观测到的试验现象也说明了这一点。例如,新做梁XL2~XL4,剪跨比均为3,配箍率0.13%~0.38%,破坏形态都为剪压型,斜裂缝宽度呈细而密的趋势变化,甚至没有较宽的临界斜裂缝,比普通混凝土梁的斜裂缝宽度明显小很多。这是由于RPC致密的微观结构,钢纤维的阻裂作用,高强箍筋较高的约束力,HRB500级纵筋较强的销栓力共同作用的结果。将表2的数据进行线性拟合,得到图9的回归曲线,修正系数a=0.503,则最大斜裂缝宽度计算公式修正为
(4)

图9 ωmax与ωu关系曲线
4结论
(1)剪跨比、配箍率、钢纤维含量和纵筋配筋率对HRB500级钢筋活性粉末混凝土简支梁的斜截面裂缝宽度都有一定的影响,剪跨比越小,试验梁的斜裂缝宽度较小,但其倾角较大;配箍率越大,试验梁的斜裂缝宽度越小;钢纤维含量越大,试验梁的斜裂缝宽度越小;纵筋配筋率越大,试验梁的斜裂缝宽度亦越小。其中钢纤维体积含量对斜裂缝宽度的影响最明显,剪跨比次之,其三是配箍率,纵筋配筋率的影响最小。
(2)在已有普通钢筋混凝土梁最大斜裂缝宽度公式的的基础上,根据试验数据,拟合出适用于HRB500级钢筋活性粉末混凝土简支梁斜裂缝宽度计算的修正系数,所建立的计算公式(4)可为同类研究提供参考。
参考文献:
[1]Yang S L, Millard S G, Soutsos M N, et al. Influence of Aggregate and Curing Regime on the Mechanical Properties of Ultra-high Performance Fiber Reinforced Concrete (UHPFRC)[J]. Construction and Building Materials, 2009,23(6):2291-2298.
[2]Dugat J,Roux N, Bernier G. Mechanical Properties of Reactive Powder Concretes[J]. Materials and Structures, 1996,29(4):233-240.
[3]杨兆鹏.活性粉末混凝土的力学性能研究[D].大连:大连交通大学,2008.
[4]李建平.超细矿粉活性粉末混凝土性能的研究[D].哈尔滨:哈尔滨工业大学,2011.
[5]P. Richard, M. Cheyrezy. Composition of Reactive Powder Concrete. Cement and Concrete Research. 1995,25(7):1491-1500.
[6]Brain F. FHWA give superior marks to concrete bride girder[J]. Civil Engineering Magazine, 2001,71(10):12-13.
[7]邓宗才,周冬至,程舒锴.配筋活性粉末混凝土梁抗剪承载力[J].哈尔滨工程大学报,2014,35(12):1512-1518.
[8]徐海宾,邓宗才,陈春生,等.超高性能纤维混凝土梁抗剪性能试验研究[J].土木工程学报,2014,47(12):91-97.
[9]金凌志,何培,祁凯能,等.高强钢筋RPC简支梁斜裂缝宽度试验研究[J].武汉大学学报(工学版),2014,47(5):665-670.
[10]张浦.基于软化桁架理论的RPC梁斜截面抗剪承载能力研究[D].北京交通大学,2011.
[11]陈彬.预应力RPC梁抗剪性能研究[D].长沙:湖南大学,2007.
[12]赵国藩.高等钢筋混凝土结构学[M].北京:机械工业出版社,2012:462-465
[13]赵国藩,李树瑶,廖婉卿.钢筋混凝土结构的裂缝控制[M].北京:海洋出版社,1991:234-237.
[14]韩嵘,赵顺波,曲福来.钢纤维混凝土抗拉性能试验研究[J].土木工程学报,2006,11(6):63-67.
收稿日期:2015-12-01; 修回日期:2015-12-15
基金项目:国家自然科学基金(51368013)
作者简介:金凌志(1959—),女,教授,研究方向为预应力与新型混凝土材料结构,E-mail:jlz-5904@163.com。 通信作者:温晴(1991—),女,硕士研究生,E-mail:alwenq@163.com。
文章编号:1004-2954(2016)07-0094-05
中图分类号:U444
文献标识码:A
DOI:10.13238/j.issn.1004-2954.2016.07.022
Research on Parameters Influencing Crack Width of Reactive Powder Concrete Beam
JIN Ling-zhi, WEN Qing
(Guangxi Key Laboratory of Geomechanics and Geotechnical Engineering College of Civil Engineering and Architecture,Guilin University of Technology, Guilin 541004, China)
Abstract:In order to analyze the influence of different parameters, such as shear span ratio, stirrup ratio, steel fiber volume ratio and longitudinal reinforcement ratio on the shear crack width of the test beam, shear tests of 4 groups of 11 HRB500 grade reinforced concrete simply supported beams are studied, and the proposed formula for calculating the width of the maximum shear crack is put forward. The research results show that shear span ratio, stirrup ratio, steel fiber volume ratio and longitudinal reinforcement ratio all have certain effects on the shear crack width of the beam. The smaller the shear span ratio, the smaller the shear crack width of the test beam. The bigger the stirrup ratio, steel fiber volume ratio and longitudinal reinforcement ratio, the smaller the shear crack width of the test beam. The effect of steel fiber volume fraction is especially obvious. The modified formula based on the calculation formula for the shear crack width of ordinary reinforced concrete beam may provide some references for the shear calculation of HRB500 Grade Reinforced reactive powder concrete simply supported beam.
Key words:HRB500; Reactive powder concrete; Influencing parameters; Shear crack width

