三维频率域可控源电磁反演研究

赵宁, 王绪本, 秦策, 阮帅

1 河南理工大学计算机学院， 焦作　454000 2 成都理工大学“油气藏地质及开发工程”国家重点实验室, 成都　610059



三维频率域可控源电磁反演研究

赵宁1, 王绪本2*, 秦策2, 阮帅2

1 河南理工大学计算机学院， 焦作454000 2 成都理工大学“油气藏地质及开发工程”国家重点实验室, 成都610059

摘要对于三维可控源电磁，反演计算效率、张量测量、旁侧效应以及阴影效应是目前研究的热点.本文正演采用基于库仑规范条件的耦合势有限体积算法，反演采用有限内存BFGS(L-BFGS)算法.合成数据反演结果表明: (1)有限内存BFGS法比非线性共轭梯度法，在反演计算效率上具有一定的优势,更适合求解大规模三维可控源电磁反演问题. (2)张量可控源电磁法相对于标量可控源电磁法，前者在模型分辨率上优于后者. (3)在某个区域无法布置测网的情况下，我们可利用旁侧效应在异常体周围布置测网进行三维反演,从而获得真实异常体的信息.同时，为避免阴影效应，我们应在测网外增加可控源电磁控制点，使得三维反演的数据更加完备.

关键词张量可控源电磁法； 三维反演； 有限内存BFGS； 旁侧效应； 阴影效应

In order to improve the 3D inversion speed, if the frequency is lower or resistivity is higher in the control equation in 3D electromagnetic forward modeling, directly dispersing the Maxwell's equations finally forms the large-scale complex coefficients sparse system of linear equations. The condition number of this system is large, which makes it difficult to converge when solving the equation. This work establishes a set of 3D finite volume algorithms based on the coupling potential to solve the problem of low number of induction. At present most linear inversion methods are based on linear search methods. How to choose the search direction is the core of the inversion method, and different search directions can yield different solutions. This paper adopts L-BFGS algorithm for inversion.

To verify the correctness of 3D numerical solution and the effectiveness of the grid design, we use a 3D program to calculate apparent resistivity and phase responses of a layered model, and make comparisons with the 1D analytical solution. According to the inversion results of synthetic data, this paper analyzes the nonlinear conjugate gradient method and limited memory quasi-Newton method, compares the tensor of the controlled source electromagnetic method and the scalar controlled source electromagnetic method, and also analyzes the influence of the lateral effect and shadow effect.

This paper presents comparison of the L-BFGS and NLCG algorithms. Firstly, we find that the execution efficiency of the L-BFGS algorithm is higher than NLCG algorithm in 3D inversion, and the L-BFGS algorithm is more suitable for dealing with 3D inversion of large amount of data. Secondly, comparing the 3D inversion results of the tensor observations and the scalar observations of survey data, we note that the former has a better effect than the latter in delineating the abnormal body and reflecting the true resistivity values. Finally, in the area in which survey network cannot be deployed, we can use the lateral effect for 3D inversion. At the same time, in order to avoid the shadow effect in the field exploration, we should use 3D inversion to deal with the real data, and add the control points of CSEM outside the survey grid.

On the basis of this work, adopting the way of encryption grid can improve the calculation accuracy. However, this will bring about more unknown parameters, and make inversion more singular. The next step, we may consider to separate the grid of forward modeling from inversion, so that the stability of the 3D inversion can be improved.

1引言

近年来，频率域可控源电磁法在油气勘探、航空近地表调查和寻找隐伏金属矿藏等方面发挥着越来越重要的作用,并使得可控源电磁法反演研究取得了长足进步.近年来，国内外学者对可控源电磁法均做了大量工作，底青云等(2004，2008)，汤井田和何继善(2005)系统介绍了可控源音频大地电磁法国内外进展及针对多维问题进行了正反演研究.林昌洪等(2012)利用视电阻率信息进行了非线性共轭梯度法(NLCG)的反演.翁爱华等(2012)利用场值信息进行了非线性共轭梯度反演.刘云鹤和殷长春(2013)采用NLCG和L-BFGS对航空电磁三维反演问题进行了对比研究，Newman和Boggs(2004)用拟牛顿法进行了电磁数据的反演解释.Egbert 和Kelbert(2012)对三维电磁反演框架进行了深入讨论.Alexander等(2014)通过直接法进行了三维可控源电磁分布式计算及实际资料处理.三维反演的计算效率问题是目前研究的重点.

三维可控源电磁反演过程中，正演计算的速度是影响反演计算效率的关键因素.正演大多采用直接法或迭代法处理大型复系数稀疏方程，针对单个发射源的可控源电磁问题，三维正演采用迭代法具有速度快，占用内存少等优点.为提高三维反演速度，反演大多采用基于线搜索的方法.在线搜索中如何选择搜索方向是反演方法的核心，且不同的搜索方向形成不同的解决方案，主要包括：最速下降法、牛顿法、非线性共轭梯度法和有限内存拟牛顿法.其中，最速下降法较简单，但收敛速度慢；牛顿法收敛速度快，但需要计算二阶偏导数矩阵，计算量大.有限内存Broyden-Fletcher-Goldfarb-Shanno(L-BFGS)(Haber ,2005)是共轭梯度法的一种推广，其本质思想是由给定的初始矩阵开始,利用一阶导数和函数信息近似二阶导数,从而不需要显式地形成Hessian矩阵，相对于利用一阶导数信息的线搜索方法，具有收敛速度快的优点.

本文首先介绍了基于耦合势的三维有限体积正演算法，其次针对L-BFGS算法的反演流程、“拟正演”计算和选择搜索步长问题进行了讨论，最后根据合成数据反演结果进行了L-BFGS与NLCG对比研究，探讨了张量测量的优势，并分析了旁侧效应和阴影效应的影响.

2正演模拟

三维电磁正演中，若控制方程中采用的频率比较低或电阻率比较高时，直接对Maxwell方程进行离散，最终形成的大型稀疏复系数线性方程组的条件数往往很大,导致方程很难收敛.

本文建立一套基于耦合势的三维有限体积算法(Weiss and Newman,2003;徐志锋和吴小平,2010).利用库仑规范条件将麦克斯韦方程变换为与其等价的矢势与标势相耦合的亥姆霍兹方程，并将其在Yee氏交错网格上进行数值离散，最终得到一个复系数稀疏线性方程组.为减少保存方程所需的内存空间，把方程存储为CSR(行压缩)格式，采用不完全LU分解预处理的对称拟最小残差法(ILU-SQMR)求解大型复系数稀疏方程.

2.1控制方程

设σ是各向同性地层中的电导率，电磁场随时间变化关系为e-iω t, ω=2πf.在均匀各向同性介质中频率域Maxwell方程为

(1)

(2)

其中μ0=4π×10-7H/m是真空中的磁导率.因为磁感应强度B是无散的，它可以表示为一个矢量的旋度，即：

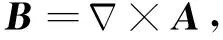
(3)

将公式(3)代入(1)中，变形得：

(4)

如上(4)式表示E-iωA为无旋的，所以它可以表示为一个标量的梯度(Aruliahetal.,2001)，即：

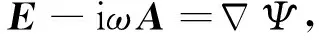
(5)

为表述方便，引入变量Φ=(iω)-1Ψ，得：

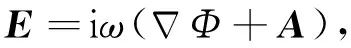
(6)

将(3)和(6)代入(2)中，得：

(7)

(8)

(9)

为了解决模拟中场源点处的奇异性问题，我们采用将总场分为一次场和二次场之和.即选择一个参考模型σ0，通过解析方法求出场源Js的响应(Ap,Φp)，然后利用一次场和参考模型求出二次场(As,Φs).二次场所满足的控制方程为

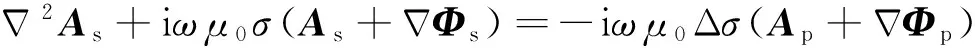
(10)

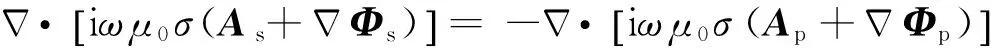
(11)

其中Δσ=σ-σ0为模型电导率与参考模型电导率之差.

2.2正确性检验

为验证三维数值解的正确性以及网格设计的有效性，我们利用三维程序计算了一个层状模型的视电阻率及相位响应，并与一维解析解进行比较.层状模型的第一层电阻率为10 Ωm，厚度为400 m，第二层电阻率为100 Ωm，空气的电阻率为2×108Ωm.如图1所示.X向的电偶极子源放置于(0,4500 m,0)处，长度1000 m，观测点坐标为(0,0,0).网格剖分为46×70×34，在观测区域和源所在区域，网格是均匀的，间距为50 m.收发距之间采用先大后小的策略，首先将网格间距逐步增加到200 m，保持15个网格，之后逐步减小到50 m，然后以因子3等比增长添加边界网格.利用此网格剖分我们分别计算了从0.01 Hz到8192 Hz共24个频率的视电阻率及相位响应，结果如图2所示.通过与解析解的对比，电阻率和相位的平均相对误差都小于2%.

本文测试计算机基本配置：CPU为Intel I7-4770K，主频3.5 GHz，内存8 GB.一次正演计算用时1小时11分钟(一次场计算耗时52 min).

3反演理论

3.1基本原理

按照Tikhonov正则化理论,地球物理反演问题可归结为求解以下目标函数的极小值问题(Avdeev,2005):

(12)

目标函数确立后，反演问题就是极小化目标函数的问题.对式(12)的目标函数求梯度得：

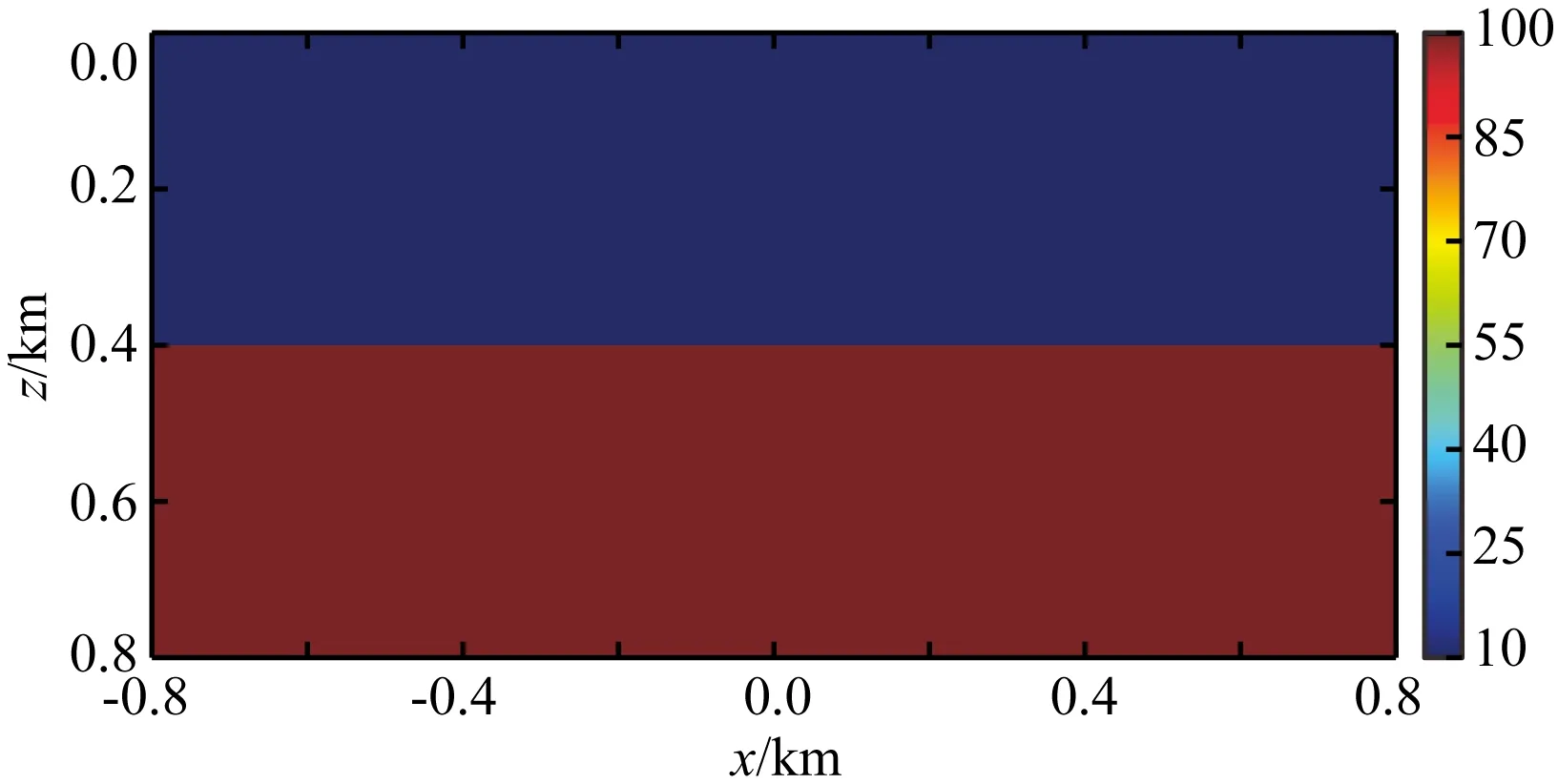
图1　三维可控源电磁正演模型

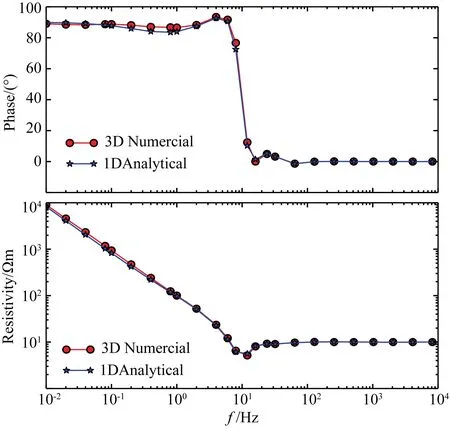
图2　三维可控源电磁正演结果验证

(13)

根据式(13)中的定义，并令A为正演响应向量的雅可比矩阵，则目标函数的梯度可进一步表示为

+2λWTW(m-m0)，

(14)

式(14)中，目标函数及其梯度信息是反演的关键信息.其主要的计算量集中在求取雅可比矩阵的转置与一个向量的乘积上，即ATq(Newman and Alumbaugh,2000; Rodi and Mackie,2001)，在附录中简述其求取过程.

3.2L-BFGS方法反演流程

针对大规模反演问题，Nocedal(1980)修正了BFGS方法并提出解决非线性最优化问题的有限内存BFGS(L-BFGS)方法.相对于BFGS方法的最大改进就是利用有限次的迭代信息修正Hessian矩阵.L-BFGS反演流程如图3所示.

对于α的要求,不能只要求f(mk+αkpk)≤f(mk),这样会导致收敛速率过慢.我们采用满足Wolfe条件的线搜索方法(JorgeandWright,2006)，公式为

(15)

(16)

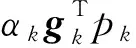
图3　三维可控源电磁L-BFGS反演流程图

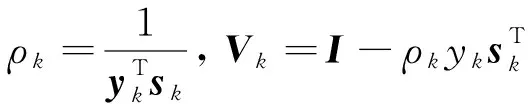
(17)

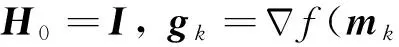
4数值算例

本文反演测试计算机配置同正演配置.反演区域与测区一致，网格剖分方式同2.2节网格剖分方式.

4.1L-BFGS与NLCG对比研究

图4模型包含两个高阻异常体和两个低阻异常体，埋深100 m，异常体大小为300 m×300 m×300 m,其中，低阻异常体电阻率为10 Ωm，高阻异常体电阻率为1000 Ωm，背景为均匀半空间，电阻率为100 Ωm.线电流源长度1000 m，坐标为(-500 m，4500 m，0)到(500 m，4500 m，0)，发射频率从0.1～4096 Hz，共15个频率.测网范围为[-800 m,-800 m,0]×[800 m,800 m,0]，共1024个物理测点，观测方式如图9a所示，反演采用的合成数据为理论数据加入5%的高斯噪声，初始模型为电阻率为100 Ωm的均匀半空间，λ为1.

图5和图6分别为NLCG和L-BFGS反演结果在XZ、YZ、XY三个平面上的切片图.如图所示，两种方法的反演结果都较好的确定了异常体的位置，其中，低阻异常体的电阻率比较接近真实电阻率值.需要指出的是，两种优化策略具有相似的内存需求(NLCG为916MB，L-BFGS为952 MB)，但是，从图7给出的目标函数值随迭代次数的变化可以看出，NLCG方法过早地陷入了局部极小，导致NLCG法在20次迭代以后，目标函数下降很慢，而L-BFGS法具有相当的稳定性.

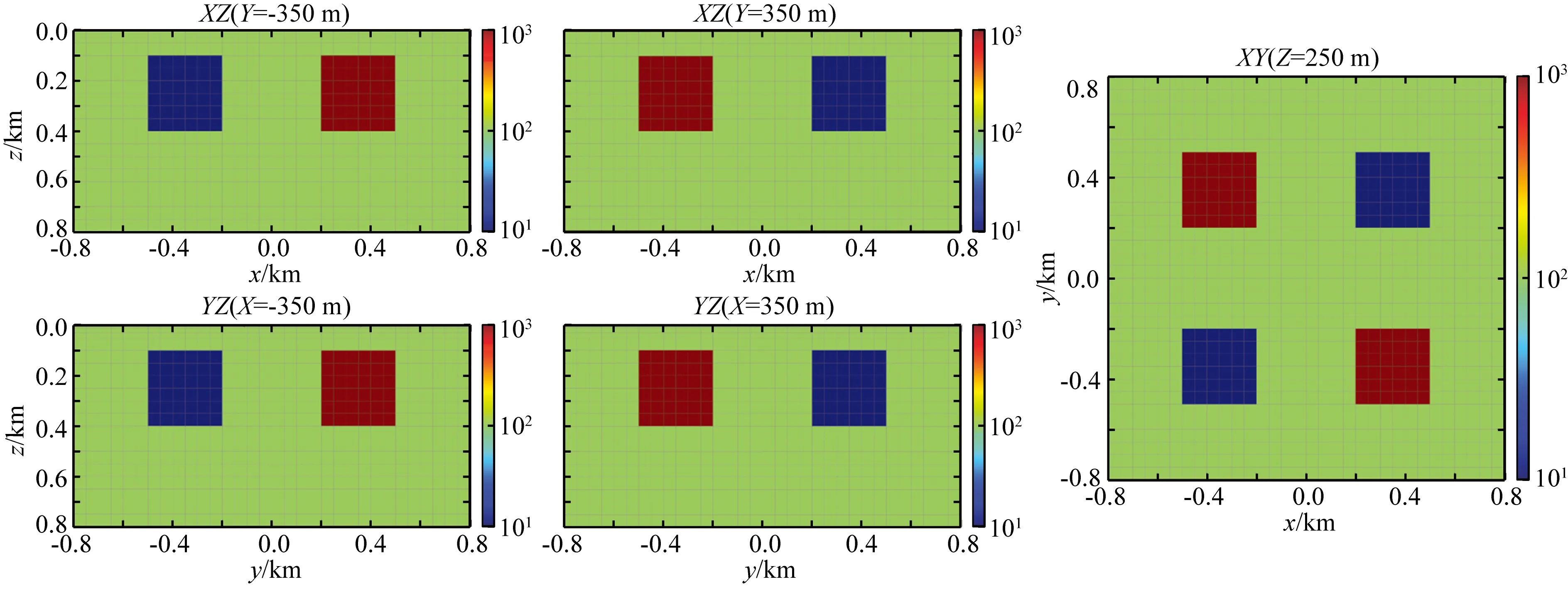
图4　4个异常体模型

图5　NLCG三维反演结果(30次迭代)

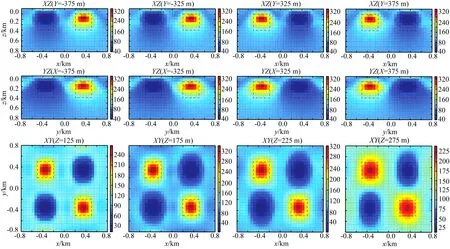
图6　L-BFGS三维反演结果(30次迭代)

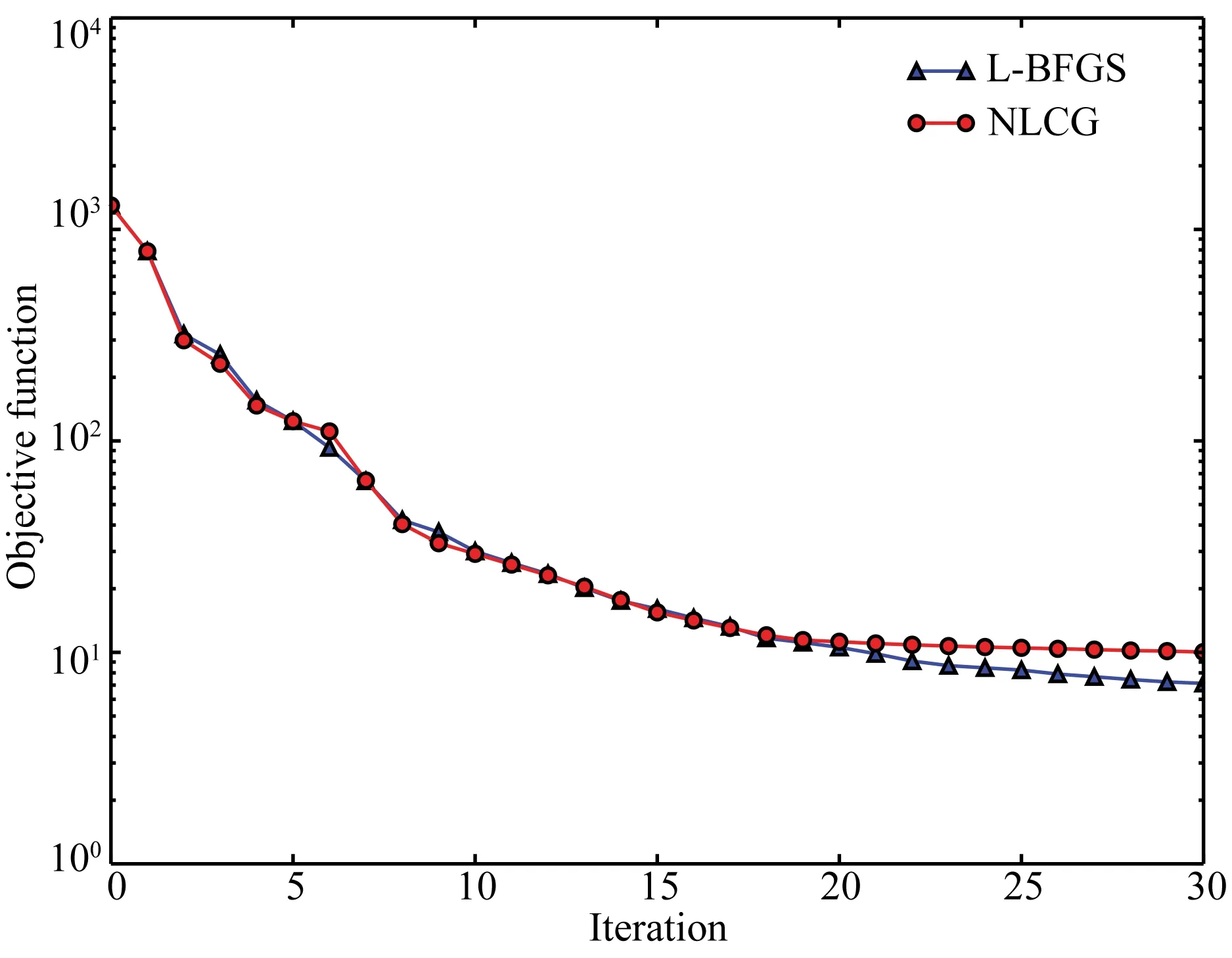
图7　L-BFGS与NLCG目标函数对比

L-BFGS方法采用1作为迭代步长就可以满足线搜索的条件，如图8a所示.相比之下，NLCG方法需要迭代步长特别小才能满足线搜索的条件.如果从求取目标函数梯度的次数来考虑反演执行效率，如图8b所示，NLCG法大多需要计算两次目标函数梯度，用时23小时31分，L-BFGS法大多只需要计算一次目标函数梯度，用时12小时17分.因此，L-BFGS方法的执行效率高于NLCG方法.

4.2张量观测

我们设计三组模型，通过两个标量测量算例和一个张量测量算例的对比，在一定程度上说明张量测量的优势.模型包含两个高阻异常体和两个低阻异常体，埋深100 m，异常体大小为300 m×300 m×300 m,其中，低阻异常体电阻率为10 Ωm，高阻异常体电阻率为1000 Ωm，背景为均匀半空间，电阻率为100 Ωm.反演采用的合成数据为理论数据加入5%的高斯噪声，初始模型为电阻率为100 Ωm的均匀半空间，λ为1.

(1)观测区域如图9a所示.综合图6结果，在z方向上，异常体的位置和电阻率控制的较好.然而，由于该观测方式，Ex、Hy分量强，Ey、Hx分量存在弱区，因此，在Y方向上，低阻体被拉长.

(2)观测区域如图9b所示.采用发射源坐标为平行于Y轴(4500 m，-500 m，0)到(4500 m，500 m，0).综合图10结果，在z方向上，异常体的位置和电阻率控制的较好.然而，由于该观测方式，Ey、Hx分量强，Ex、Hy分量存在弱区，在X方向上，低阻体被拉长.

(3)观测区域如图9c所示.采用发射源坐标分别为平行于X轴(-500 m，4500 m，0)到(500 m，4500 m，0)；平行于Y轴(4500 m，-500 m，0)到(4500 m，500 m，0).综合图11结果，发射源采用两个不同的且相距很远的极化.通过张量数据的三维反演结果与标量数据的三维结果对比，张量测量对于恢复真实异常体模型(特别是圈定异常体边界)要好于标量测量.

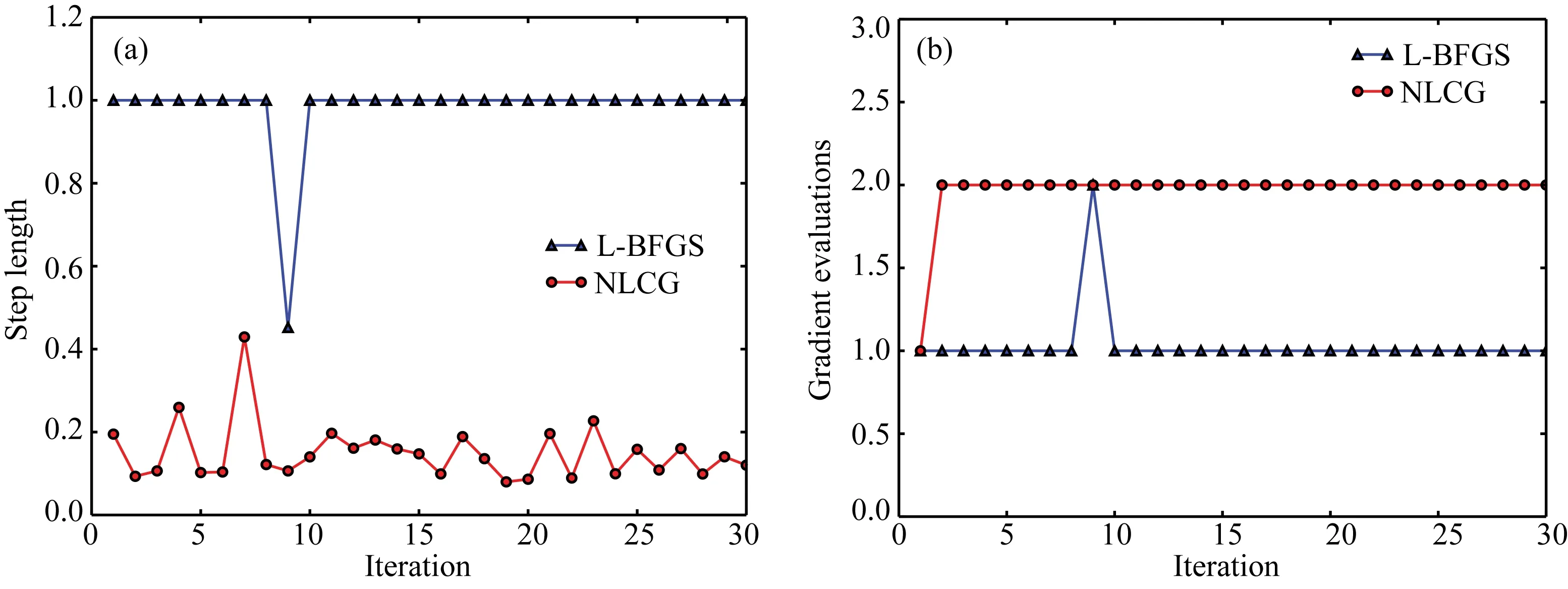
图8　反演中步长和目标函数梯度随迭代次数变化(a)步长随迭代次数变化；(b)目标函数梯度随迭代次数变化.

图9　观测装置平面图

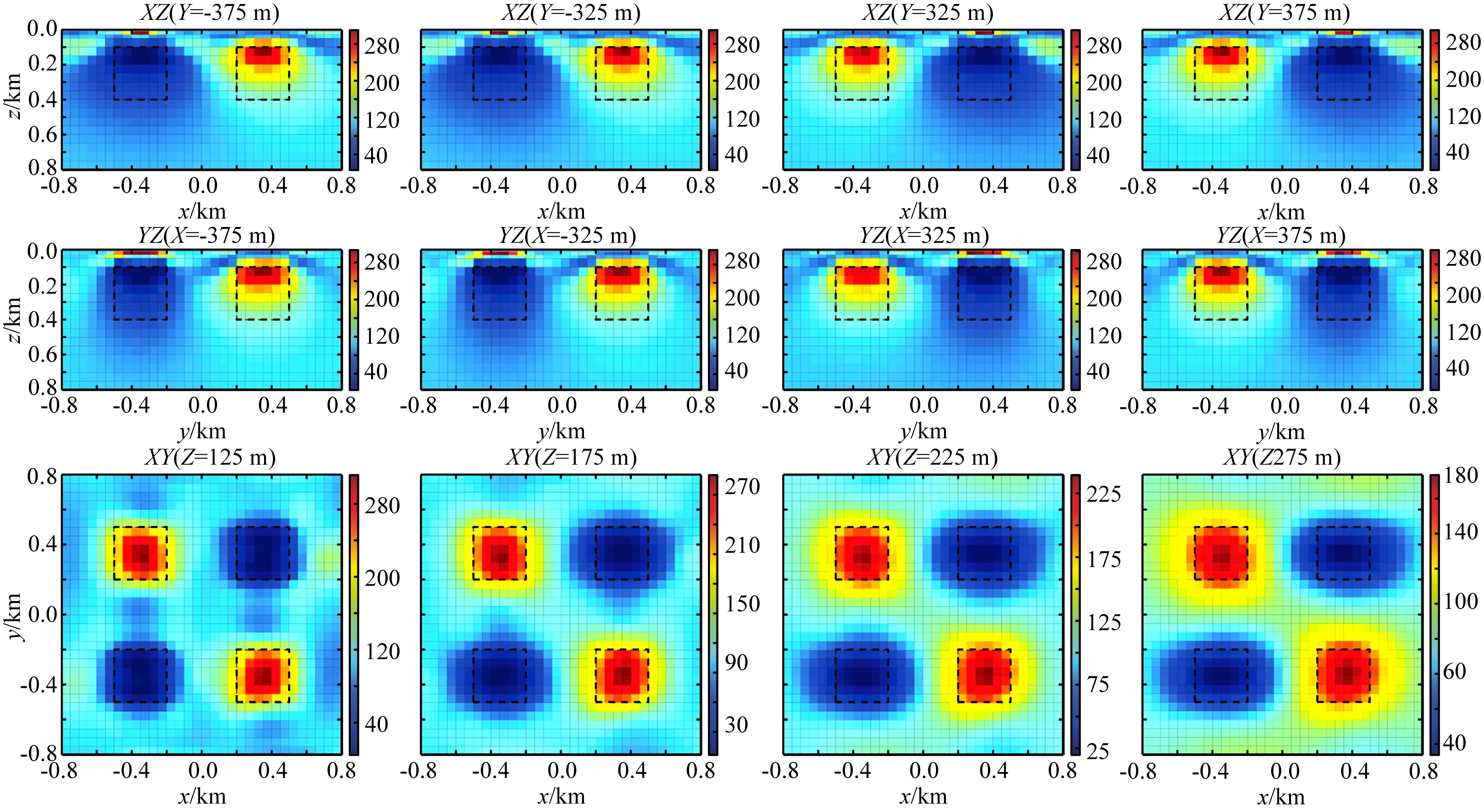
图10　观测装置2的反演结果

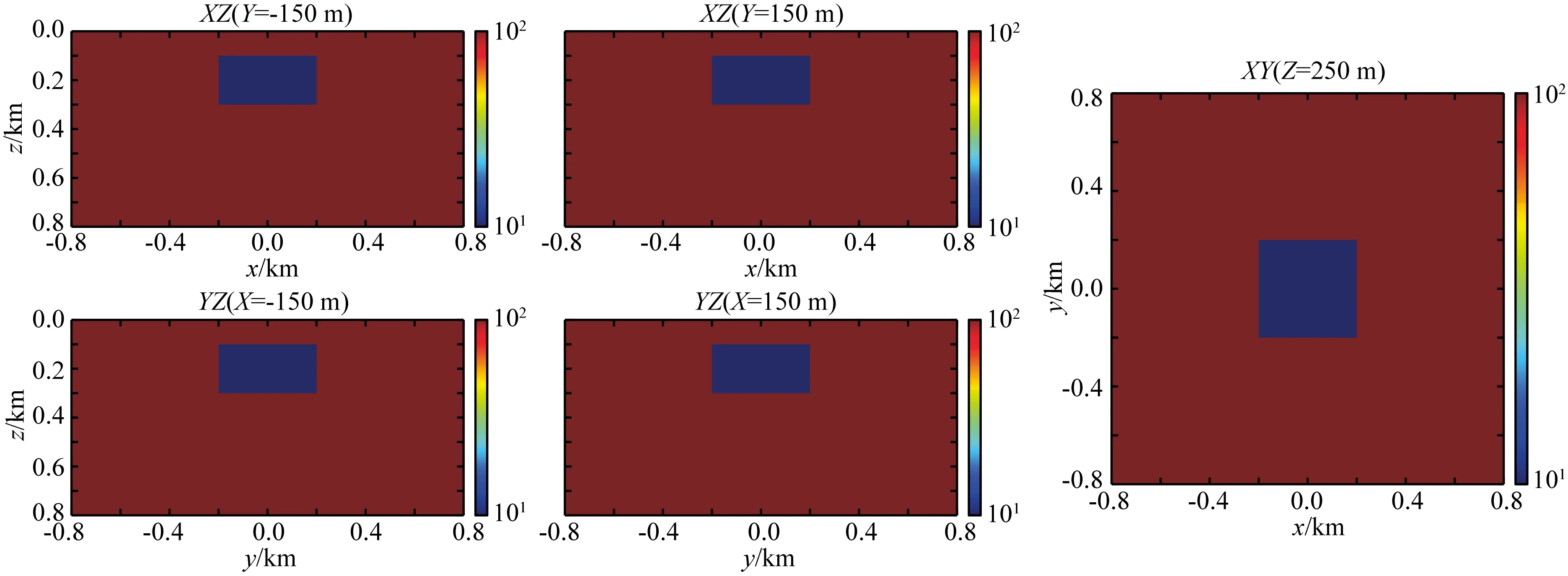
图12　异常体模型

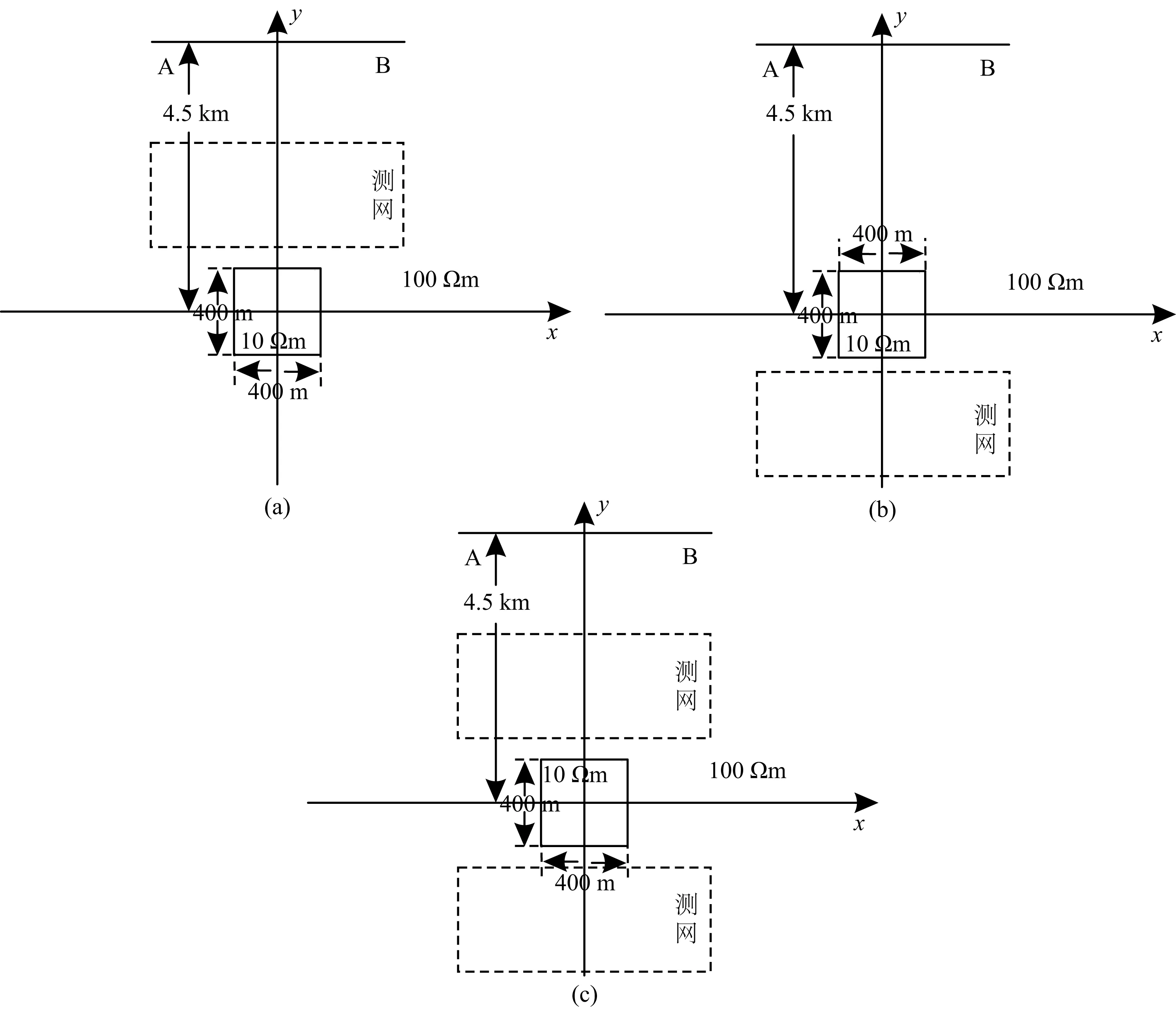
图13　观测方式2平面图

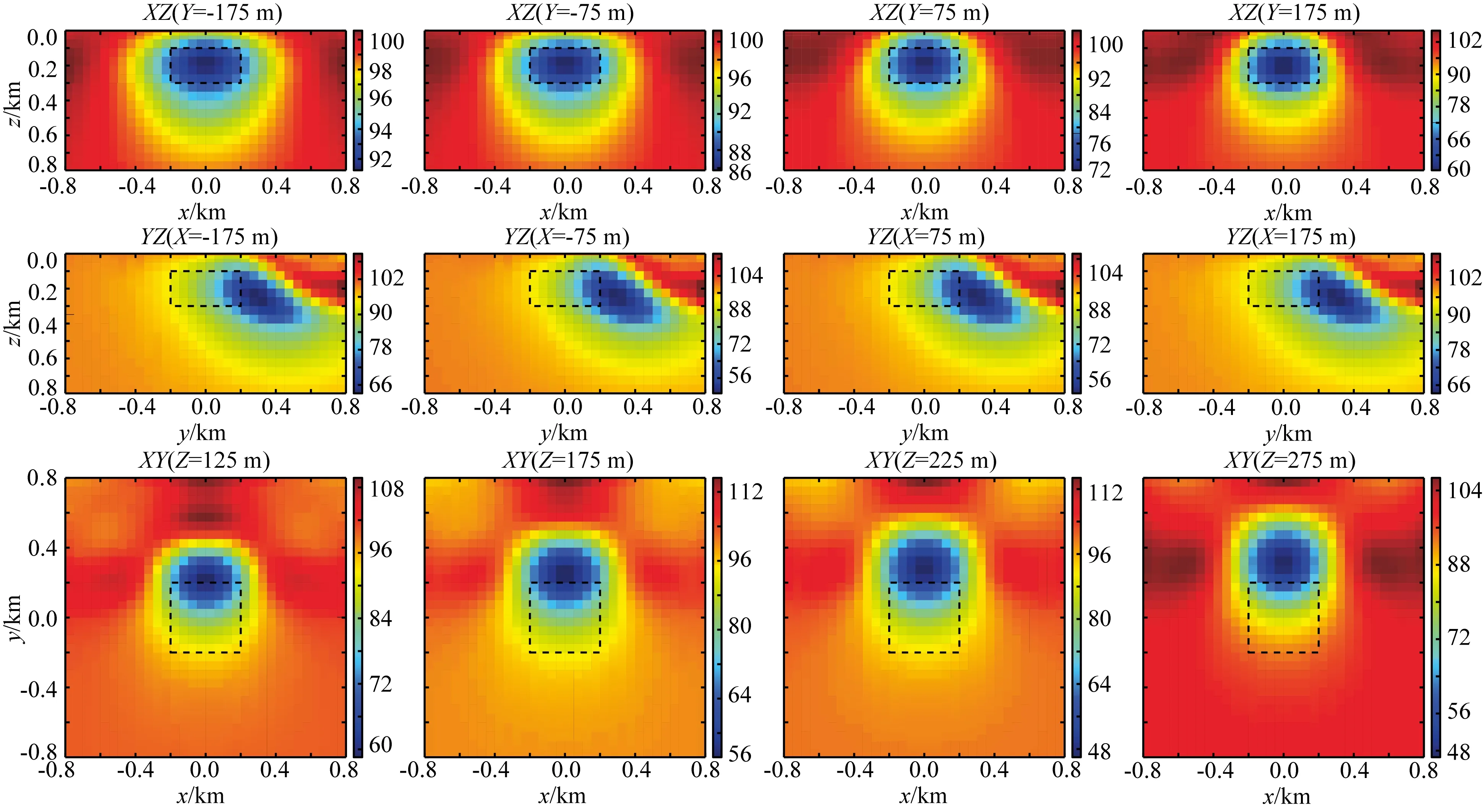
图14　观测方式一反演结果

图15　观测方式二反演结果

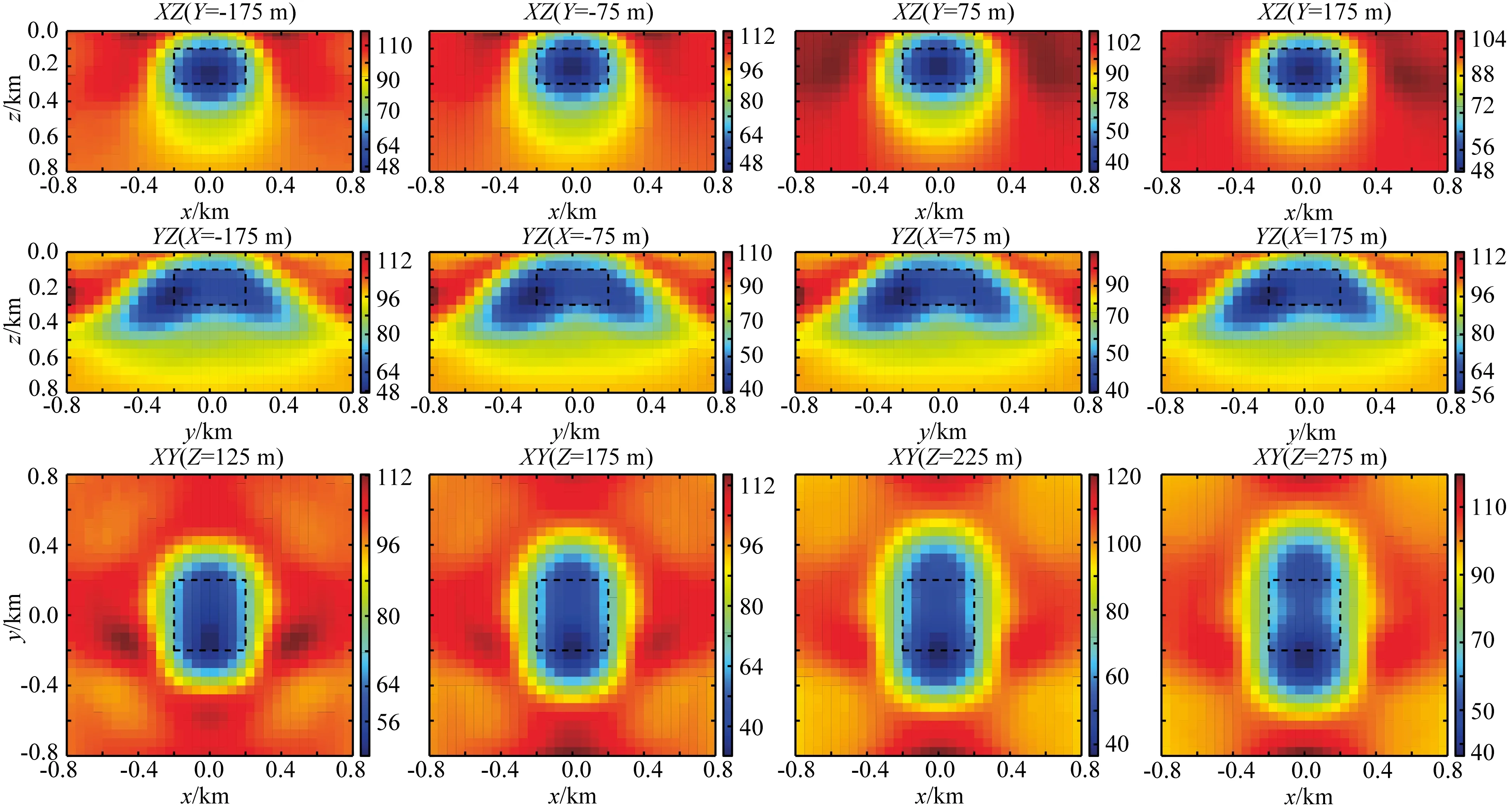
图16　观测方式三反演结果

4.3旁侧效应

在实际工作中，某个区域可能无法布置测网，设计一组模型进行三维反演用以讨论旁侧效应的效果.测试模型为均匀半空间背景中有一个低阻异常体，如图12所示.异常体埋深100 m，大小为200 m×200 m×200 m,其中，低阻异常体电阻率为10 Ωm，背景电阻率为100 Ωm.线电流源长度1000 m，坐标为(-500 m，4500 m，0)到(500 m，4500 m，0)，发射频率从0.1 Hz～4096 Hz，共15个频率.反演采用的合成数据为理论数据加入5%的高斯噪声，初始模型为电阻率为100 Ωm的均匀半空间.正则化因子为1.测网分为3种：

(1)X从-800 m到800 m，Y从325 m到800 m,如图13a.

(2)X从-800 m到800 m，Y从-800 m到-325 m,如图13b.

(3)X从-800 m到800 m，Y从-800 m到-325 m；X从-800 m到800 m，Y从325 m到800 m,如图13c.

首先，在异常体两边分别布置测网，利用旁侧效应进行三维反演，反演结果如图14和15所示，反演出的异常位置偏离异常体真实位置，并偏向所布置测网的下方.然后，在异常两边同时布置测网，反演结果如图16所示，反演出的异常位置相对准确，电阻率值也相对于图14和15有较好的结果.

同时，我们利用三维反演处理实际数据过程中，阴影效应会影响反演结果，如图15所示.为了避免阴影效应的影响，从图16中所得结果，我们应该在测网外增加可控源电磁控制点，使得三维反演具有足够完备的数据，从而减弱阴影效应的影响.

5总结

本文正演采用基于耦合势的有限体积方法，反演采用L-BFGS方法.首先，通过L-BFGS算法与NLCG算法对比分析，发现三维反演中L-BFGS比NLCG算法的执行效率更高，更适合处理三维大数据量的反演问题.其次，针对测网数据，张量观测相对于标量观测，前者的三维反演结果相对于后者，对圈定异常体边界和反映真实电阻率值具有更好的效果.最后，针对无法布置测点区域，可利用旁侧效应进行三维反演.同时，实际生产中为避免阴影效应影响，应该采用三维反演处理实际数据，并在测网外增加CSEM的控制点.在本文工作的基础上，为提高计算精度，可采用加密网格的方式，然而，这样会带来更多的未知量，导致反演会更加奇异，下一步可考虑将正演模型网格和反演网格分离(Commer and Newman,2008),进而提高三维反演的稳定性.

致谢向两位审稿人对本文提出的修改意见表示衷心感谢.

附录AATq计算

在正演过程中，令

Ke=s，

(A1)

表示由Maxwell方程组离散得到的线性方程组，其中，e为电场分量构成的向量，s为源项.为了使反演更加稳定，我们定义正演响应为视电阻率的自然对数，即：

(A2)

向量ai和bi表示将e组合为观测点处的Ex和Hy的插值向量.在此我们认为插值向量和模型无关，则：

(A3)

其中向量ci定义为

(A4)

从式(A1)中我们可以得到

(A5)

将上式代入式(A3)中，得：

(A6)

令向量ui满足：

Kui=si，

(A7)

利用矩阵K的对称性，将式(A6)重写为

(A8)

根据式(A8)，我们得到：

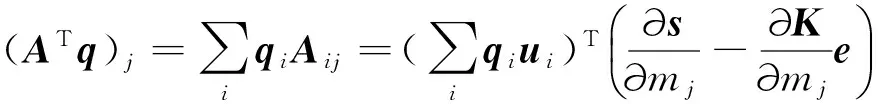
(A9)

令向量r满足：

(A10)

则：

(A11)

References

Aruliah D A, Ascher U M, Haber E A, et al. 2001. A method for the forward modeling of 3D electromagnetic quasi-static problems.MathematicalModelsandMethodsinAppliedSciences, 11(1): 1-21, doi: 10.1142/S0218202501000702.Avdeev D B. 2005. Three dimensional electromagnetic modeling and inversion from theory to application.Surv.Geophys., 26(6): 767-799, doi: 10.1007/s10712005-1836-x. Commer M, Newman G A. 2008. New advances in three dimensional controlled-source electromagnetic inversion.Geophys.J.Int., 172(2): 513-535, doi: 10.1111/j.1365-246X.2007.03663.x. Di Q Y, Unsworth M, Wang M Y. 2004. 2.5D CSAMT modeling with the finite element method over 2-D complex earth media.ChineseJ.Geophys. (in Chinese), 47(4): 723-730, doi: 10.3321/j.issn:0001-5733.2004.04.026.

Di Q Y , Wang R.2008. The modeling, inversion and application of Controlled Source Audio-frequency MagnetoTellurics. Beijing: Science Press.Egbert G D, Kelbert A. 2012. Computational recipes for electromagnetic inverse problems.Geophys.J.Int., 189(1): 251-267, doi: 10.1111/j.1365-246X.2011.05347. x.

Grayver A V, Streich R, Ritter O. 2014. 3D inversion and resolution analysis of land-based CSEM data from the Ketzin CO2storage formation.Geophysics, 79(2): E101-E114, doi: 10.1190/GEO2013-0184.1. Haber E. 2005. Quasi-Newton methods for large-scale electromagnetic inverse problems.InverseProblems, 21(1): 305-323, doi: 10.1088/0266-5611/21/1/019.Lin C H, Tan H D, Shu Q, et al. 2012. Three-dimensional conjugate gradient inversion of CSAMT data.ChineseJ.Geophys. (in Chinese), 55(11): 3829-3838, doi: 10.6038/j.issn.0001-5733.2012.11.030.

Liu Y H, Yin C C. 2013. 3D inversion for frequency-domain HEM data.ChineseJ.Geophys. (in Chinese), 56(12): 4278-4287, doi: 10.6038/cjg20131230. Newman G A, Alumbaugh D L. 2000. Three dimensional magnetotelluric inversion using non-linear conjugate gradients.Geophys.J.Int., 140(2): 410-424, doi: 10.1046/j.1365-246x.2000.00007.x.

Newman G A, Boggs P T. 2004. Solution accelerators for large scale three dimensional electromagnetic inverse problems.InverseProblems, 20(6): 151-170, doi: 10.1088/0266-5611/20/6/S10.

Nocedal J. 1980. Updating quasi-Newton matrices with limited storage.MathematicsofComputation, 35(151): 773-782, doi: 10.1090/S0025-5718-1980-0572855-7.

Nocedal J, Wright S J. 2006. Numerical Optimization (2nd ed). New York: Springer Verlag.

Rodi W L, Mackie R L. 2001. Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion.Geophysics, 66(1): 174-187, doi: 10.1190/1.1444893.

Sasaki Y. 2001. Full 3D inversion of electromagnetic data on PC.JournalofAppliedGeophysics, 46(1): 45-54, doi: 10.1016/S0926-9851(00)00038-0.

Tang J T, He J S. 2005. The Method and Application of Controlled Source Audio-frequency Magneto Tellurics. Changsha: Central South University Press.

Weiss C J, Newman G A. 2003. Electro-magnetic induction in a generalized 3D anisotropic earth, Part 2: The LIN pre-condition.Geophysics, 68(3): 922-930, doi: 10.1190/1.1581044.

Weng A H, Liu Y H, Jia D Y, et al. 2012. Three-dimensional controlled source electromagnetic inversion using non-linear conjugate gradients.ChineseJ.Geophys. (in Chinese), 55(10): 3506-3515, doi: 10.6038/j.issn.0001-5733.2012.10.034.Xu Z F, Wu X P. 2010. Controlled source electromagnetic 3D modeling in frequency domain by finite element method.ChineseJ.Geophys. (in Chinese), 53(8): 1931-1939, doi: 10.3969/j.issn.0001-5733.2010.08.019.

附中文参考文献

底青云, Unsworth M, 王妙月. 2004. 复杂介质有限元法2. 5维可控源音频大地电磁法数值模拟. 地球物理学报, 47(4): 723-730, doi: 10.3321/j.issn:0001-5733.2004.04.026.

底青云, 王若. 2008. 可控源音频大地电磁数据正反演及方法应用. 北京: 科学出版社.

林昌洪, 谭捍东, 舒晴等. 2012. 可控源音频大地电磁三维共轭梯度反演研究. 地球物理学报, 55(11): 3829-3839, doi: 10.6038/j.issn.0001-5733.2012.11.030.

刘云鹤, 殷长春. 2013. 三维频率域航空电磁反演研究. 地球物理学报, 56(12): 4278-4287, doi: 10.6038 /cjg20131230.

汤井田, 何继善. 2005. 可控源音频大地电磁法及其应用. 长沙: 中南大学出版社.

翁爱华, 刘云鹤, 贾定宇等. 2012. 地面可控源频率测深三维非线性共轭梯度反演. 地球物理学报, 55(10): 3506-3515, doi: 10.6038/j.issn.0001-5733.2012.10.034.

徐志锋, 吴小平. 2010. 可控源电磁三维频率域有限元模拟. 地球物理学报, 53(8): 1931-1939, doi: 10.3969/j.issn.0001-5733.2010.08.019.

(本文编辑张正峰)

基金项目国家自然科学基金重点项目(U1262206)和河南理工大学博士基金资助.

作者简介赵宁，男，1982年生，博士，讲师，主要从事电磁法正反演方法研究. E-mail: zhaoning@hpu.edu.cn *通讯作者王绪本，男，1956年生，教授，博士生导师，主要从事地球物理学研究. E-mail: wxb@cdut.edu.cn

doi:10.6038/cjg20160128 中图分类号P631

收稿日期2014-07-17，2015-05-13收修定稿

3D frequency-domain CSEM inversion

ZHAO Ning1, WANG Xu-Ben2*, QIN Ce2， RUAN Shuai2

1CollegeofComputer,HenanPolytechnicUniversity,Jiaozuo454000,China2StateKeyLaboratoryofOilandGasReservoirGeologyandExploitation,ChengduUniversityofTechnology,Chengdu610059,China

AbstractRecently, the frequency domain controlled-source electromagnetic method is playing an increasingly important role in oil and gas exploration, aviation near-surface survey and search for concealed metallic deposits. For three-dimensional controlled-source electromagnetic (3D-CSEM) inversion, the computation efficiency of inversion, tensor measurement, lateral effect and shadow effect are focused topics in recent research of this technology.

KeywordsTensor CSEM; 3D inversion; L-BFGS; Lateral effect; Shadow effect

赵宁, 王绪本, 秦策等. 2016. 三维频率域可控源电磁反演研究.地球物理学报，59(1):330-341,doi:10.6038/cjg20160128.

Zhao N, Wang X B, Qin C, et al. 2016. 3D frequency-domain CSEM inversion.ChineseJ.Geophys. (in Chinese),59(1):330-341,doi:10.6038/cjg20160128.