基于基追踪弹性阻抗反演的深部储层流体识别方法
刘晓晶, 印兴耀, 吴国忱, 宗兆云
中国石油大学(华东)地球科学与技术学院, 青岛 266580
基于基追踪弹性阻抗反演的深部储层流体识别方法
刘晓晶, 印兴耀, 吴国忱, 宗兆云
中国石油大学(华东)地球科学与技术学院, 青岛266580
摘要深部储层地震资料通常照明度低、信噪比低、分辨率不足,尤其是缺乏大角度入射信息,对深部储层流体识别存在较大影响.Gassmann流体项是储层流体识别的重要参数,针对深层地震资料的特点,本文首先在孔隙介质理论的指导下,推导了基于Gassmann流体项与剪切模量的两项AVO近似方程.通过模型分析,验证了该方程在小角度时与精确Zoeppritz方程误差很小,满足小角度入射条件下的近似精度要求.然后借助Connolly推导弹性阻抗的思想,推导了基于Gassmann流体项与剪切模量的两项弹性阻抗方程.针对深部储层地震资料信噪比差的特点,利用奇偶反射系数分解实现了深部储层基追踪弹性阻抗反演方法,最后提出了基于基追踪弹性阻抗反演的Gassmann流体项与剪切模量的求取方法,并将提取的Gassmann流体项应用于深部储层流体识别.模型测试和实际应用表明该方法稳定有效,具有较好的实用性.
关键词深部储层; 两项AVO近似; 两项弹性阻抗方程; 基追踪; 流体识别
According to the theory of porous media, thef-μtwo-term AVO approximate equation is derived in terms of Gassmann fluid term (f) and shear modulus (μ). We make a comparison of the reflection coefficients calculated by Zoeppritz equation,f-μ-ρthree-term approximation andf-μtwo-term approximation. As elastic impedance (EI) inversion is more reliable than AVO/AVA inversion, we derive the two-term elastic impedance equation based on the idea proposed by Connolly. The model constrained basis pursuit inversion is proposed for elastic impedance inversion, which can improve the stability of inversion for elastic impedance. After implementing the inversion for two-angle elastic impedance, we present the fluid factor and shear modulus extraction method by utilizing the two-term elastic impedance equation. We use the well log to confirm the validity of our method. Finally, we apply the method to a real deep reservoir data to identify the fluid saturated in the reservoir.
The derived two-parameter equation is close to the Zoeppritz equation when the angle of incidence is less than 20°, and it has almost the same accuracy asf-μ-ρthree-term approximation equation. Therefore, thef-μtwo-parameter approximation can be used for fluid factor estimation. It is clear that the method of fluid factor and shear modulus extraction is stable and the estimates match well with the real model from the model test. The results of real data application match well with the well data interpretation and the blocky inversion results generated by the model constrained basis pursuit method have a good resolving power to the layers.
We simplify thef-μ-ρthree-term approximate equation intof-μtwo-term approximate equation which is suitable for deep reservoirs. The accuracy of the new approximate equation is almost the same as thef-μ-ρapproximate equation. The model constrained basis pursuit inversion method yields the blocky layer which has the advantage in interpretation. The tests on synthetic data and field data show that the estimates are reliable and can be used for fluid discrimination for deep reservoirs.
1引言
随着能源需求加大,深部储层逐渐成为重要的研究目标,探索深部储层的叠前地震反演方法与储层流体识别方法成为当前研究的热点.
流体因子成为当前“定量”储层流体识别的重要方法.Smith和Gidlow(1987)利用纵横波速度相对变化的加权差识别储层流体,并首先提出了“流体因子”的概念;Fatti等(1994)对Smith和Gidlow(1987)提出的流体因子重新定义为纵横波阻抗反射系数的加权叠加.这两种流体因子是属于界面型流体因子,反映的是储层流体的边界.为了反演储层流体的层内信息,专家学者提出了多种流体因子用于储层的流体识别.Goodway等(1997)提出LMR流体识别技术;Russell等(2003)基于等效多孔介质理论对Gassmann方程进行简化、推导,提出Russell流体因子ρf;Quakenbush 等 (2006)提出通过旋转纵横波阻抗坐标轴得到泊松阻抗,并用于流体识别;Russell等(2011)对流体因子进行了深入讨论,提出直接使用Gassmann流体项f进行流体识别.国内学者宁忠华等(2006)对流体识别进行了深入研究,构建高灵敏度流体因子;张世鑫(2012)针对流体因子的识别精度受储层物性的影响的问题,提出使用等效流体模量Kf进行流体识别,但该方法需要至少四个角度的叠前地震数据;印兴耀等(2013a)基于双相介质理论对流体识别进行了相关研究.专家学者们的众多研究成果表明,Gassmann流体项f对储层敏感,有较好的流体识别效果,因而,本文利用Gassmann流体项f对深部储层进行流体识别.
叠前地震反演是获取储层敏感弹性参数的重要方法,在储层预测和流体识别方面发挥着极其重要的作用.其中,基于Zoeppritz方程或其近似式的AVO反演结果稳定、分辨率高,专家学者对不同的介质类型进行了进一步研究(Yin et al., 2013; 印兴耀等, 2013b),但利用叠前道集反演对噪声敏感;而弹性阻抗反演使用角度部分叠加资料,实现方便、稳定性高,并且在抗噪能力上比AVO反演更具有优势(Cambois, 2000).自从Connolly(1999)提出了弹性阻抗的概念以来,人们对弹性阻抗反演进行大量的研究(Savic et al., 2000; Li et al., 2012; Zong et al., 2012),并从弹性阻抗中提取弹性参数获取储层弹性信息(李爱山等, 2008; Yin et al., 2004; 宗兆云等, 2011).针对常规间接计算流体因子误差累计问题,印兴耀等(2010)提出流体弹性阻抗反演方法,直接提取Gassmann流体项,提高了流体识别的精度.针对非均质储层,Yin等(2014)提出了迭代式Gassmann流体项直接反演与流体识别方法.
弹性阻抗反演技术在浅层勘探中已经趋于成熟,而在深部储层目标区,地震资料的照明角度小、有效覆盖次数低、信噪比低、分辨率不足、缺乏大偏移距(角度)等信息,叠前地震资料所蕴含的AVO信息量不够,这给叠前地震反演带来了新的挑战.Lu和 McMechan(2004)认为密度项并不是一个独立的参数,将其与纵横波速度相乘得到纵横波阻抗,并利用经验公式拟合密度项,基于两项弹性阻抗反演纵横波阻抗.李爱山等(2009)基于Lu的思想,针对东营工区,拟合密度项经验公式,利用两个角度弹性阻抗反演纵横波阻抗,并用于深部含气储层的预测.高刚等(2013)推导了基于纵横波阻抗的两项式弹性阻抗方程,并将其用于深层碳酸盐岩储层预测.印兴耀等(2013b)针对深部储层的流体识别,提出了基于两项弹性阻抗Russell流体因子直接估算方法.
基于多孔介质理论得到的Gassmann流体项f具有较高的流体敏感性,本文将其作为深部储层流体识别因子.在前人研究的基础上,利用岩石物理经验关系,降低方程未知参数的个数,推导了基于Gassmann流体项f与剪切模量μ的两项AVO方程,并基于Connolly的思想推导f-μ两项弹性阻抗方程,最后利用两项弹性阻抗方程直接提取Gassmann流体项f与剪切模量μ,为深部储层流体识别提供敏感、可靠的数据基础.
2f-μ两项AVO近似方程
2.1f-μ两项近似公式推导
实际的岩石是包含固体和流体的双相介质,Gassmann(1951)提出了关于波在多孔介质中的传播的孔隙弹性理论,建立了Gassmann方程.Russell等(2011)基于该孔隙弹性理论,提出将Gassmann流体项f作为流体因子用于流体识别,Gassmann流体项f表达式为
(1)
对(1)式进行进一步推导可得:
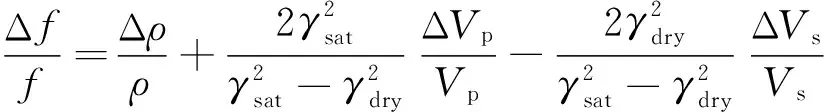
(2)
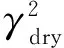
(3)
其中μ为剪切模量,Δμ/μ为剪切模量反射系数.
(4)
其中,a、r1为实际工区的密度与纵波速度数据的拟合系数.由上式推导可得:
(5)
Zhang等(2012)在推导射线弹性阻抗时应用如下假设:
(6)
其中,r2为横波速度反射系数与密度反射系数之间的拟合系数.将式(6)代入式(3)可以得到剪切模量与密度之间的关系为
(7)
将式(5)与式(6)代入式(2)可以得到Gassmann流体项与密度之间的关系为
(8)
Russell等(2011)基于Gassmann流体项f、剪切模量μ与密度ρ推导了f-μ-ρ三项AVO近似方程:
(9)
其中,Rpp为反射系数,θ为入射角.
为了计算简便,将式Russell近似中密度项系数写为
(10)
所以,Russell近似可写作:
(11)
将式(7)与式(8)代入式(11)可以得到基于Gassmann流体项与剪切模量的f-μ两项AVO近似方程为
(12)

(12)
2.2f-μ两项近似方程精度分析
为了验证新的两项近似AVO方程的精度,设计了三层砂岩模型对f-μ两项近似方程、Zoeppritz精确方程和Russell近似方程进行精度分析,模型参数如表1所示.模型的中间层为低阻抗含气砂岩,上覆地层和下伏地层为高阻抗的含水砂岩.因此,含气砂岩的顶界面为负波阻抗界面,底界面为正波阻抗界面.分别利用Zoeppritz方程、Russell近似公式以及本文推导出的f-μ两项AVO近似公式进行计算表1中含气砂岩顶、底界面的反射系数(图1a、图2a所示),并计算Russell近似方程与f-μ两项近似方程相对于精确Zoeppritz方程计算反射系数的差值(图1b、图2b所示).从图中可以看出,在入射角不大于20o时,f-μ两项近似与Russell近似精度相当,两者计算的反射系数数曲线几乎重合,而随着入射角度的增加,这两种近似与Zoeppritz方程的误差逐渐增大.因此,在入射角不大于20o时,f-μ两项近似对Zoeppritz方程有较好的近似,其精度误差在可接受范围内,满足小角度近似精度要求,因而,公式适用于深层小角度反演.

表1 三层砂岩模型参数

图1 含气砂岩顶界面反射系数对比(a) 不同近似方程计算反射系数对比; (b) 反射系数差值对比.
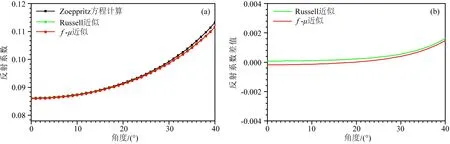
图2 含气砂岩底界面反射系数对比(a) 不同近似方程计算反射系数对比; (b) 反射系数差值对比.
3基追踪弹性阻抗反演
3.1f-μ两项弹性阻抗方程
为了在小角度近似条件下稳定求取Gassmann流体项,将公式推导为两项弹性阻抗方程.Connolly(1999)提出弹性阻抗的概念,并通过式(13)的假设,基于Aki-Richards近似(Aki and Richards, 1980)推导了基于纵横波速度与密度的弹性阻抗方程,公式(13)为
(13)
上式建立了叠前反射系数与弹性阻抗之间的关系,其中,Rpp为反射系数,θ为入射角,EI为弹性阻抗.本文借助Connolly(1999)推导弹性阻抗方程的思想,推导基于Gassmann流体项与剪切模量的f-μ两项弹性阻抗方程为
(14)
采用Whitcombe(2002)弹性阻抗正规化方法,将式弹性阻抗方程进行正规化,使其量纲与纵波阻抗相一致:
(15)
其中,f0、μ0分别为f与μ的平均值;A0为弹性阻抗正规化参数,其表达式为
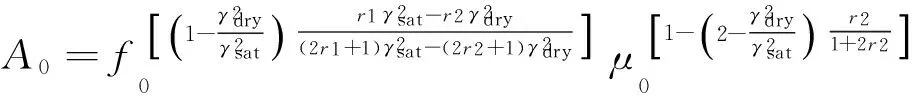
(16)
由式(15)可知,当入射角θ=0°时,弹性阻抗的取值为常规的声阻抗,当入射角θ>0°时,弹性阻抗的量纲与声阻抗的量纲是一致的.
一般认为Gassmann流体项受孔隙流体影响,对流体敏感性较高,可用于储层流体识别,剪切模量反映的是岩石骨架信息,不受孔隙流体的影响,对流体的敏感性较差.公式包含了与孔隙流体相关的Gassmann流体项以及与孔隙流体无关的剪切模量,根据该式(15)可直接提取Gassmann流体项进而进行流体识别.
3.2基追踪弹性阻抗反演方法
基于式(15)直接估算Gassmann流体项f首先需要进行弹性阻抗反演.本文在Zhang和Castagna(2011)提出的基追踪稀疏层反演的基础上,在目标函数中加入模型约束,增强反演的稳定性与反演结果横向连续性.如图3所示,对反射层顶底界面反射系数进行奇偶分量分解,其奇偶分量分别表示为
(17)
其中re为偶反射脉冲对,即偶分量;ro为奇反射脉冲对,即奇分量;δ(t)为单位脉冲函数;Δt为采样间隔,i为顶界面所在的采样点位置,j为反射层厚度的采样点个数,i+j表示底界面所在的采样点位置.
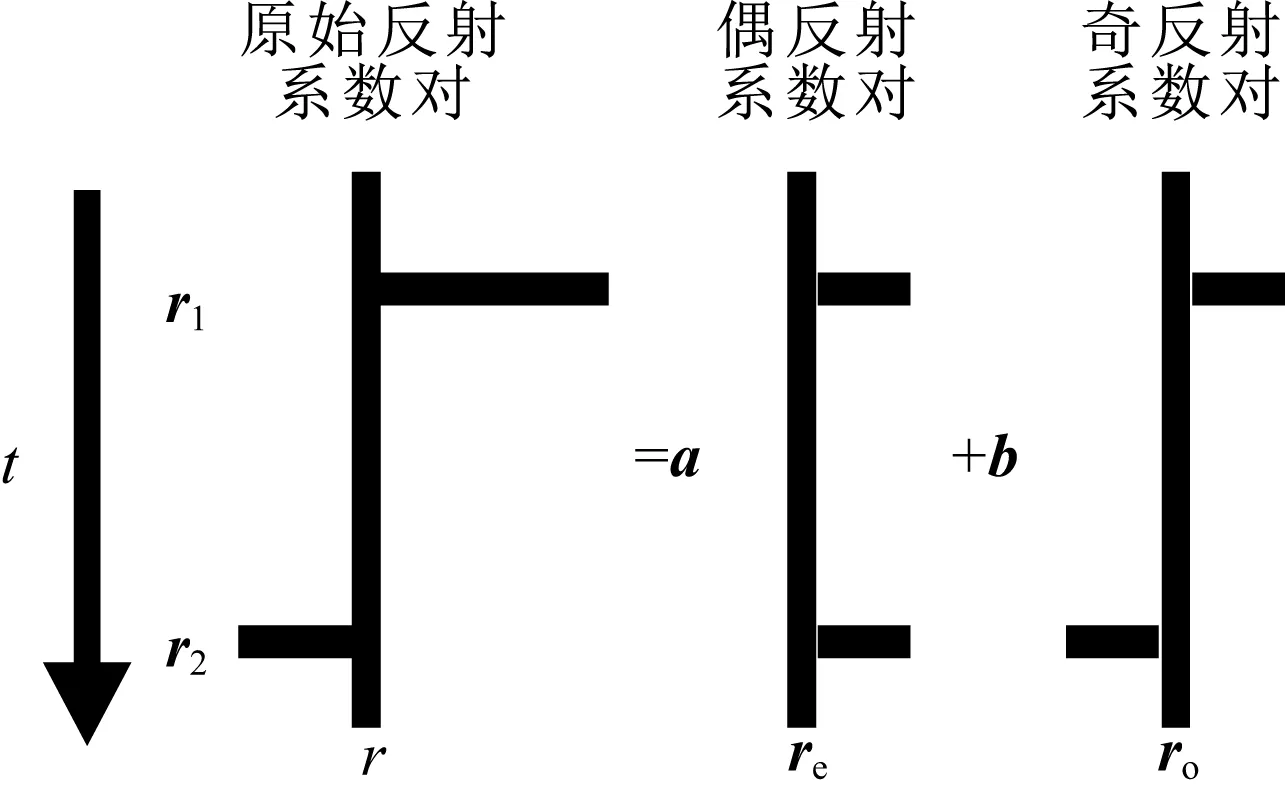
图3 反射系数奇偶分量分解(Zhang and Castagna, 2011)
(18)
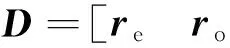
考虑褶积模型d=Wr,W为子波矩阵,r为反射系数序列,将(18)式代入褶积模型,并令G=WD,考虑地下反射层是稀疏的,在L1范数的约束下,建立基追踪反演目标函数为
(19)
其中,λ为稀疏约束系数.为了增强反演的稳定性,本文在(19)式中加入弹性阻抗模型约束,得到模型约束与稀疏约束联合约束下的基追踪弹性阻抗反演目标函数为
(20)
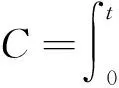
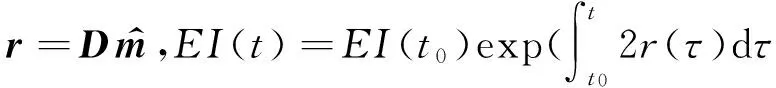
(21)
深部储层地震资料缺乏大角度入射信息,针对小角度和中角度部分叠加地震数据分别使用上述方法进行弹性阻抗反演,可以得到两个角度的绝对弹性阻抗数据.该方法反演得到的反射系数具有较好的稀疏性,弹性阻抗呈现块化,对地层分界面具有较强分辨能力,能够在一定程度上适应深部储层地震数据低信噪比的特点.
4参数提取
由于式(15)中弹性阻抗与流体项和剪切模量呈非线性关系,为了能从弹性阻抗数据中提取Gassmann流体因子并用于流体识别,对式两侧取自然对数,将其进行线性化为
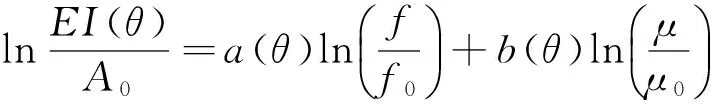
(22)
针对深层两个角度θ1与θ2矩阵求解公式为
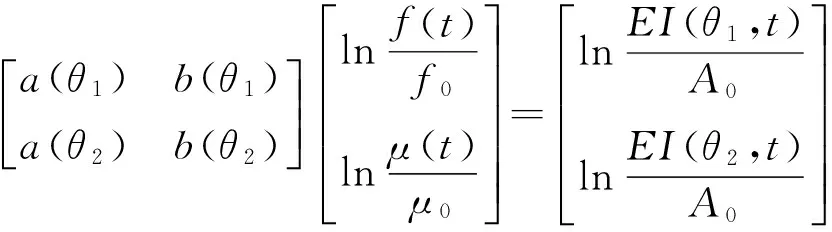
(23)
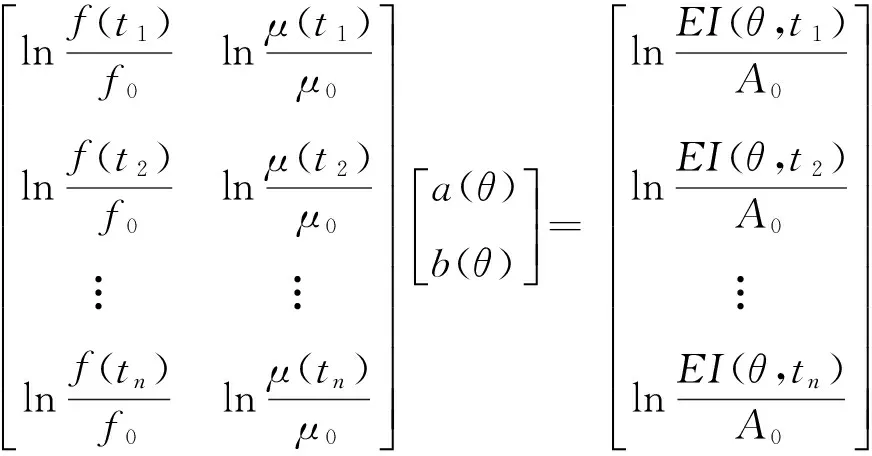
(24)
分别将两个角度的弹性阻抗井旁道数据代入(24)式结合测井曲线计算出系数矩阵A,并将系数矩阵A代入式(23),利用最小二乘法即可直接提取Gassmann流体项f与剪切模量μ.
5模型测试
利用测井数据合成两个角度(5°、15°)的弹性阻抗,如图4a和b所示.图4c和d中红色曲线分别为利用本文提出的基于两个角度弹性阻抗提取的Gassmann流体项与剪切模量,黑色曲线为测井曲线计算得到的Gassmann流体项与剪切模量,比较反演结果与原始模型可以发现两者几乎重合,误差很小.实际应用中,弹性阻抗由地震数据反演得到,不可避免会含有噪声.因此,为了测试利用两项弹性阻抗提取Gassmann流体项与剪切模量对噪声的敏感性,将图4a和b中的弹性阻抗分别加入噪声得到信噪比分别为20∶1与10∶1的含噪声弹性阻抗数据,如图5a和b与图6a和b所示.利用本文提出的方法提取的Gassmann流体项与剪切模量分别如图5c和d与图6c和d中红色曲线所示.图5c和d与图6c和d中黑色曲线与图4c和d中黑色曲线意义相同,为利用已知测井曲线计算的Gassmann流体项与剪切模量.分别比较不同信噪比情况下的反演结果与原始模型,可以发现,随着噪声的增加,提取的Gassmann流体项与剪切模量中的噪声也会增加,提取的弹性参数的精度逐渐降低,但反演结果依然与原始模型具有很高的吻合度.因此,利用本文的方法可以稳定、可靠地提取Gassmann流体项f与剪切模量μ,为利用叠前地震资料对深部储层流体识别提供可靠的数据基础.
6实际资料应用
将本方法应用于某实际工区,该工区目的层埋深达到4000m以上,发育了一系列的砂砾岩扇体(如图8a中黑色椭圆内所示),深水砂砾岩体的扇中亚相成为主要储集空间,油气藏类型属于以砂砾岩体为主导的隐蔽油气藏.选择工区内过A井与B井连井剖面验证该方法的在实际应用中的有效性.测井解释结果中A井无油气显示,B井解释为含气层,深度约为4350m,对应于地震剖面中时间约3.21s,如图8中所示.利用Dillon等(2003)提出流体因子敏感性定量分析方法对A、B两井的测井资料进行分析比较了弹性参数对气层的敏感性,如图7所示,发现Gassmann流体项对含气层最为敏感.图8a和b分别为两个角度部分叠加地震数据,对应角度分别为4°与20°.首先对这两个角度部分叠加地震数据分别利用模型约束基追踪反演方法进行弹性阻抗反演,得到两个角度的弹性阻抗,然后利用本文提出的方法基于两个角度的弹性阻抗提取Gassmann流体项与剪切模量.图8c为反演得到的Gassmann流体项,从图中可以看出Gassmann流体项剖面对气层的识别效果显著,Gassmann流体项异常值沿沙砾岩体分布,图中红色椭圆内B井井旁道流体识别效果与测井解释结果相一致,在非沙砾岩体发育区并无流体异常显示.图8d为提取得到的剪切模量,由于剪切模量对含气储层并不敏感,因而在红色椭圆内B井井旁道并无气层异常显示,与常规认识结论相一致.A井解释结果无流体显示,无论在Gassmann流体项与剪切模量剖面上A井井旁道均无异常显示.因此,本文提出的利用两个角度弹性阻抗提取Gassmann流体项与剪切模量方法是可靠的,在实际工区中应用效果明显,可为深部储层的流体识别提供可靠的数据基础.
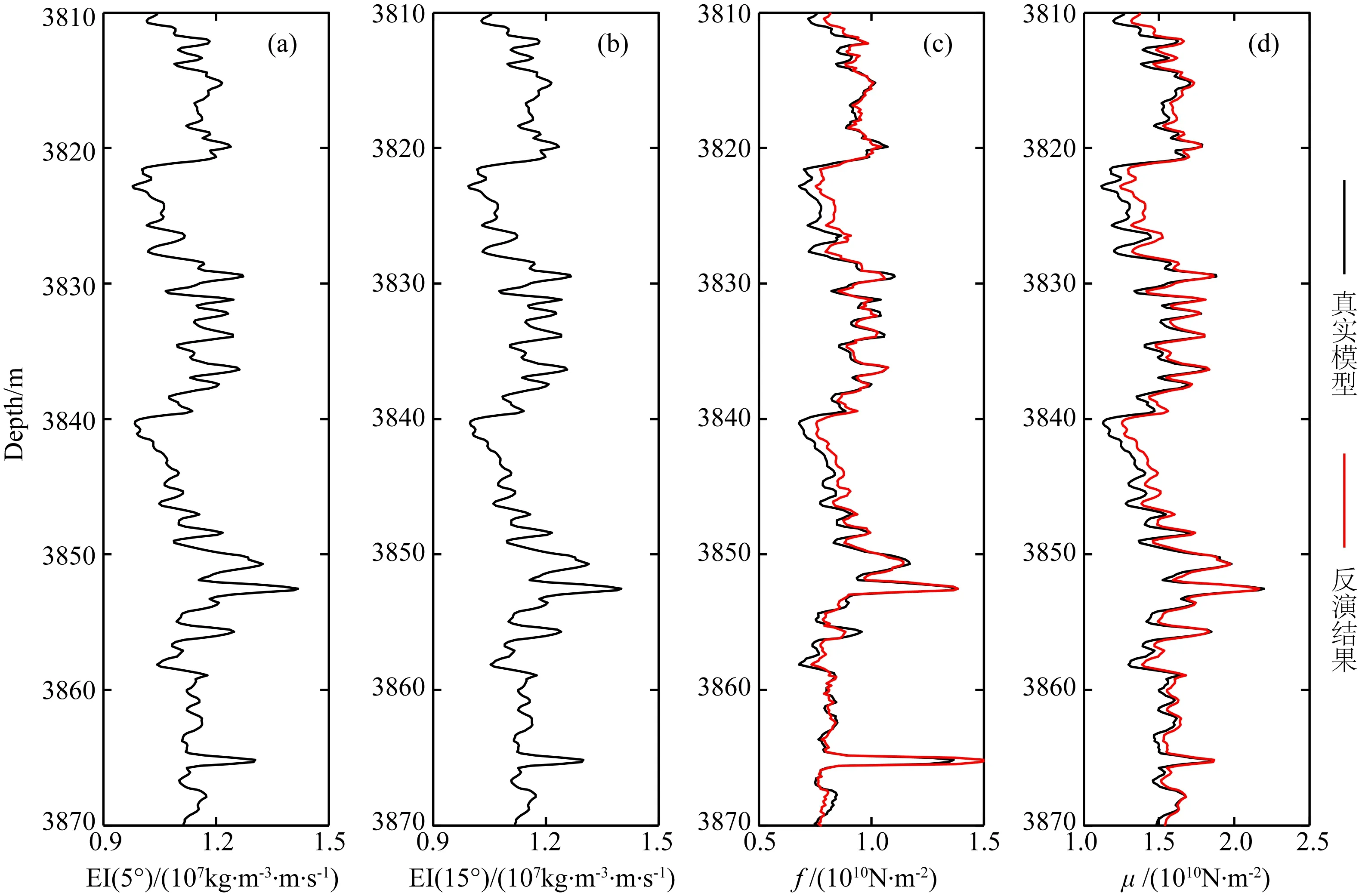
图4 无噪声两个角度弹性阻抗以及参数提取结果
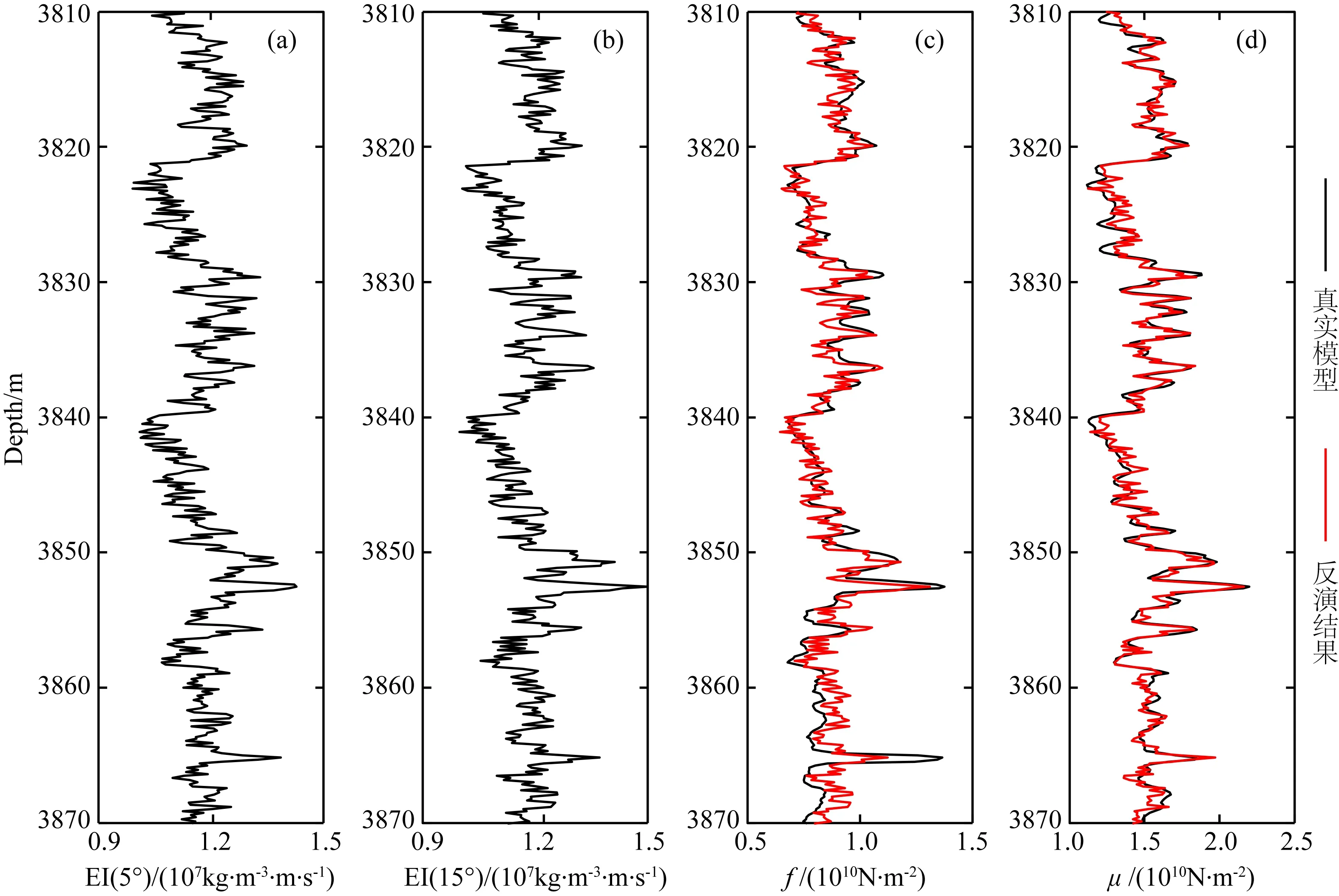
图5 含噪声两个角度弹性阻抗以及参数提取结果(SN=20∶1)
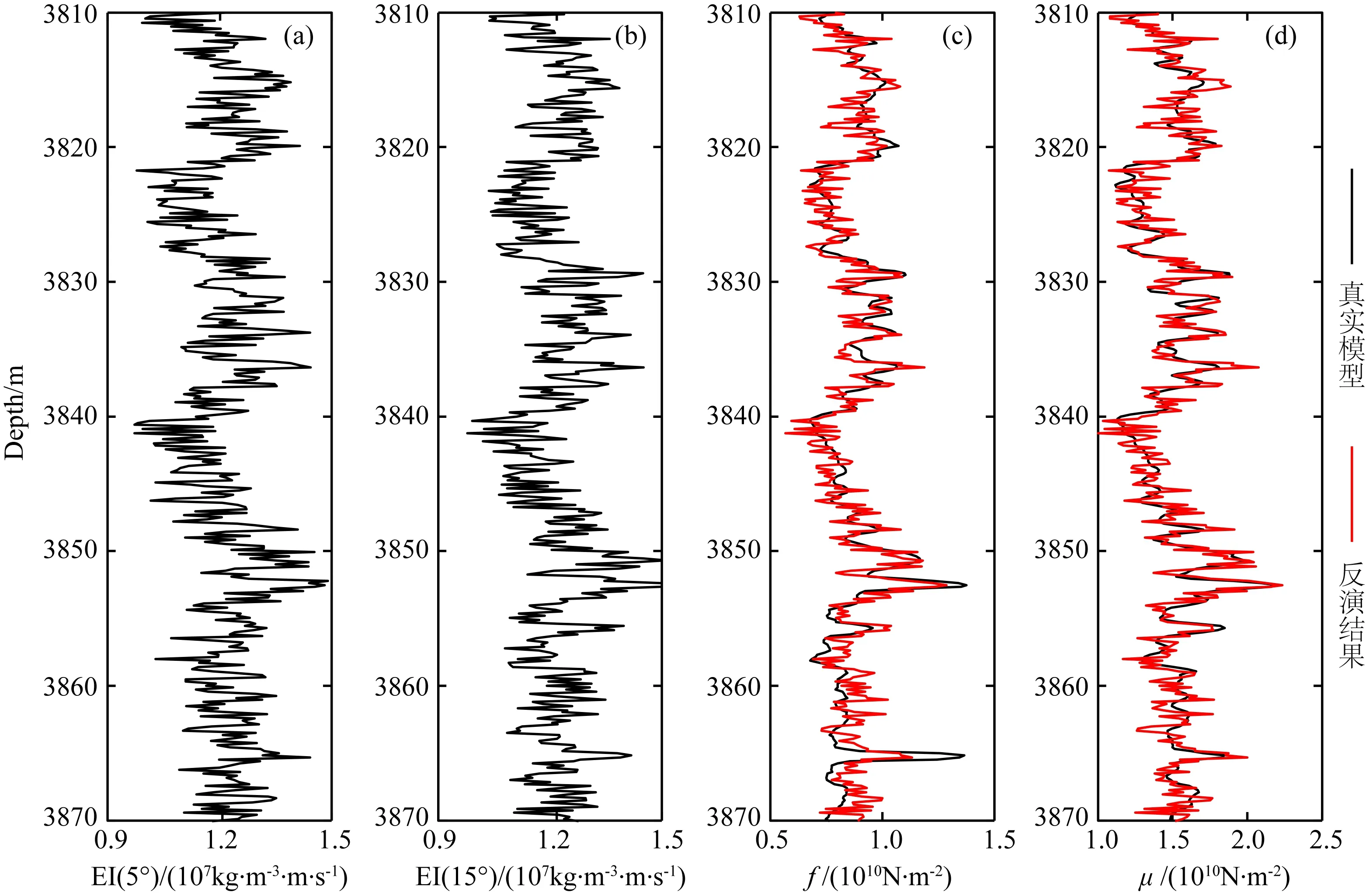
图6 含噪声两个角度弹性阻抗几参数提取结果(SN=10∶1)

图7 流体敏感性分析
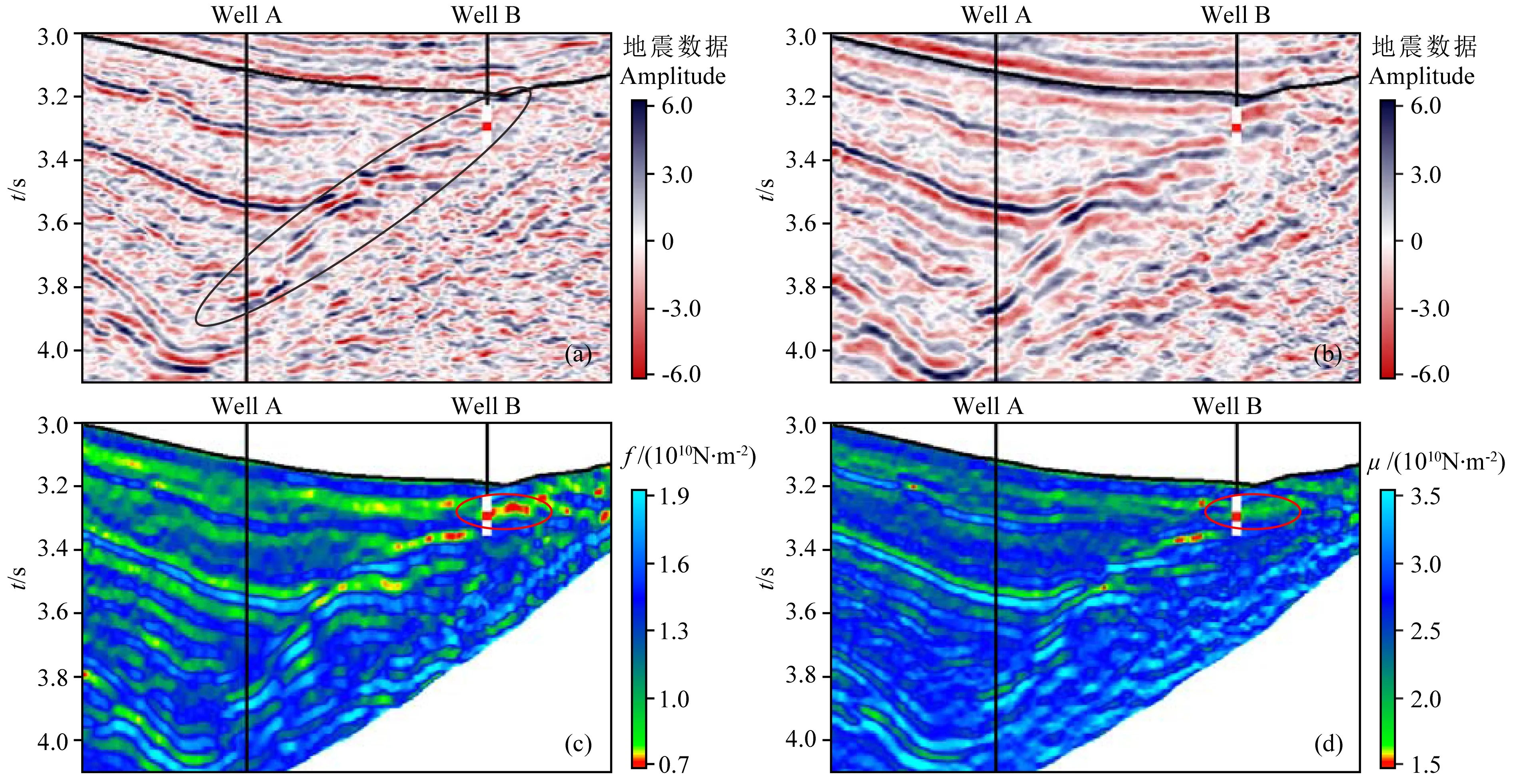
图8 利用两个角度弹性阻抗提取Gassmann流体项在数据中的应用(a) 小角度地震数据; (b) 中角度地震数据; (c) Gassmann流体项剖面; (d) 剪切模量剖面.
7结论
(1) 本文使用的弹性阻抗反演方法为模型约束下基追踪反演方法,该方法是在基追踪反演方法的基础上加入了模型约束,反演结果更为可靠,进而有利于提取Gassmann流体项与剪切模量的准确性,最终提高深层流体识别精度.
(2)Gassmann流体项对储层流体有较高的敏感性,是储层流体识别的重要参数.本文考虑了深层地震资料照明度低、缺乏大偏移距信息等特点,推导了基于Gassmann流体项f与剪切模量μ的两项AVO近似方程,减少了方程待求参数个数,该方程可以满足深层小角度入射的近似精度要求,并推导了f-μ两项弹性阻抗方程,提出利用两个角度弹性阻抗反演Gassmann流体项与剪切模量的方法.模型测试表明该方法具有较强的稳定性,并且提取的Gassmann流体项在深部储层实际资料应用中效果明显.
References
Aki K, Richards P G. 1980. Quantitative Seismology. San Francisco: W. H. Freeman. Cambois G. 2000. AVO inversion and elastic impedance.∥ 70th Annual International Meeting, Society of Exploration Geophysicists. Expanded Abstracts, 142-145.Connolly P. 1999. Elastic impedance.TheLeadingEdge, 18(4): 438-452.
Dillon L, Schwedersky G, Vásquez G, et al. 2003. A multiscale DHI elastic attributes evaluation.TheLeadingEdge, 22(10): 1024-1029.
Fatti J L, Smith G C, Vail P J, et al. 1994. Detection of gas in sandstone reservoirs using AVO analysis: A 3-D seismic case history using the Geostack technique.Geophysics, 59(9): 1362-1376.
Gao G, He Z H, Cao J X, et al. 2013. The new two-term elastic impedance inversion and its application to predict deep gas-bearing carbonate reservoirs.OilGeophysicalProspecting(in Chinese), 48(3): 450-457.
Gassmann F. 1951. Elastic waves through a packing of spheres.Geophysics, 16(4): 673-685.
Goodway B, Chen T, Downton J. 1997. Improved AVO fluid detection and lithology discrimination using Lamé petrophysical parameters; “λρ”, “μρ”, & “λ/μfluid stack”, from P and S inversions.∥ 67th Annual International Meeting, Society of Exploration Geophysicists. Expanded Abstracts, 183-186.
Li A S, Yin X Y, Lu N, et al. 2009. Application of elastic impedance inversion with two angle stack gathers to predict gas-bearing reservoir of mid-deep layer.OilGeophysicalProspecting(in Chinese), 44(1): 87-92.Li A S, Yin X Y, Zhang F C, et al. 2008. Elastic impedance in VTI media and parameter extraction.ProgressinGeophysics(in Chinese), 23(6): 1878-1885.
Li C, Yin X Y, Zhang G Z. 2012. Elastic impedance equation based on the incident-angle approximation and inversion.∥ 74th EAGE Conference & Exhibition.
Lu S M, McMechan G A. 2004. Elastic impedance inversion of multichannel seismic data from unconsolidated sediments containing gas hydrate and free gas.Geophysics, 69(1): 164-179.Ning Z H, He Z H, Huang D J. 2006. High sensitive fluid identification based on seismic data.GeophysicalProspectingforPetroleum(in Chinese), 45(3): 239-241.
Quakenbush M, Shang B, Tuttle C. 2006. Poisson impedance.TheLeadingEdge, 25(2): 128-138.
Russell B H, Gray D, Hampson D P. 2011. Linearized AVO and poroelasticity.Geophysics, 76(3): C19-C29.
Russell B H, Hedlin K, Hilterman F J, et al. 2003. Fluid-property discrimination with AVO: A Biot-Gassmann perspective.Geophysics, 68(1): 29-39.Savic M, VerWest B, Masters R, et al. 2000. Elastic impedance inversion in practice.∥ 70th Annual International Meeting, Society of Exploration Geophysicists. Expanded Abstracts, 689-692.
Smith G C, Gidlow P M. 1987. Weighted stacking for rock property estimation and detection of gas.GeophysicalProspecting, 35(9): 993-1014.
Whitcombe D N. 2002. Elastic impedance normalization.Geophysics, 67(1): 60-62.
Yin X Y, Li C, Zhang S X. 2013a. Seismic fluid discrimination based on two-phase media theory.JournalofChinaUniversityofPetroleum(EditionofNaturalScience) (in Chinese), 37(5): 38-43.
Yin X Y, Yuan S H, Zhang F C. 2004. Extracting petrophysical parameters from elastic impedance.∥ CPS/SEG 2004 International Geophysical Conference. Expanded Abstracts. 538-542.Yin X Y, Zhang S X, Zhang F. 2013b. Two-term elastic impedance inversion and Russell fluid factor direct estimation method for deep reservoir fluid identification.ChineseJournalofGeophysics(in Chinese), 56(7): 2378-2390, doi: 10.6038/cjg20130724.
Yin X Y, Zhang S X, Zhang F C, et al. 2010. Utilizing Russell approximation based elastic wave impedance inversion to conduct reservoir description and fluid identification.OilGeophysicalProspecting(in Chinese), 45(3): 373-380.
Yin X Y, Zong Z Y, Wu G C. 2013. Improving seismic interpretation: a high-contrast approximation to the reflection coefficient of a plane longitudinal wave.PetroleumScience, 10(4): 466-476.
Yin X Y, Zong Z Y, Wu G C. 2014. Seismic wave scattering inversion for fluid factor of heterogeneous media.ScienceChina:EarthSciences, 57(3): 542-549.
Zhang F, Wang Y H, Li X Y. 2012. Viabilities of seismic ray impedance and elastic impedance for hydrocarbon-sand discrimination.Geophysics, 77(4): M39-M52.Zhang R, Castagna J. 2011. Seismic sparse-layer reflectivity inversion using basis pursuit decomposition.Geophysics, 76(6): R147-R158.Zhang S X. 2012. Methodology and application of fluid identification with seismic information [Ph. D. thesis]. Qingdao: China University of Petroleum (Huadong).Zong Z Y, Yin X Y, Wu G C. 2012. Elastic impedance variation with angle inversion for elastic parameters.JournalofGeophysicsandEngineering, 9(3): 247-260.
Zong Z Y, Yin X Y, Zhang F C. 2011. Elastic impedance Bayesian inversion for lame parameters extracting.OilGeophysicalProspecting(in Chinese), 46(4): 598-604.
附中文参考文献
高刚, 贺振华, 曹俊兴等. 2013. 两项式弹性波阻抗反演方法在深层碳酸盐岩储层预测中的应用. 石油地球物理勘探, 48(3): 450-457.
李爱山, 印兴耀, 陆娜等. 2009. 两个角度弹性阻抗反演在中深层含气储层预测中的应用. 石油地球物理勘探, 44(1): 87-92.
李爱山, 印兴耀, 张繁昌等. 2008. VTI介质中的弹性阻抗与参数提取. 地球物理学进展, 23(6): 1878-1885.
宁忠华, 贺振华, 黄德济. 2006. 基于地震资料的高灵敏度流体识别因子. 石油物探, 45(3): 239-241.
印兴耀, 李超, 张世鑫. 2013a. 基于双相介质的地震流体识别. 中国石油大学学报(自然科学版), 37(5): 38-43.
印兴耀, 张世鑫, 张峰. 2013b. 针对深层流体识别的两项弹性阻抗反演与Russell流体因子直接估算方法研究. 地球物理学报, 56(7): 2378-2390, doi: 10.6038/cjg20130724.
印兴耀, 张世鑫, 张繁昌等. 2010. 利用基于Russell近似的弹性波阻抗反演进行储层描述和流体识别. 石油地球物理勘探, 45(3): 373-380.
张世鑫. 2012. 基于地震信息的流体识别方法研究与应用[博士论文]. 青岛: 中国石油大学(华东).
宗兆云, 印兴耀, 张繁昌. 2011. 基于弹性阻抗贝叶斯反演的拉梅参数提取方法研究. 石油地球物理勘探, 46(4): 598-604.
(本文编辑张正峰)
基金项目国家自然科学基金石油化工联合基金重点项目(U1562215),国家重点基础研究发展计划(973)项目(2013CB228604),国家科技重大专项(2011ZX05030-004-002,2011ZX05006-002,2011ZX05009-003),中国博士后基金,青岛市博士后启动项目及中石化重点实验室基金(WTYJY-WX2014)联合资助.
作者简介刘晓晶,男,1988年生,博士研究生,主要从事地球物理理论、方法与应用方面研究工作.E-mail:xiaojingliu.1122@gmail.com
doi:10.6038/cjg20160123 中图分类号P631
收稿日期2015-02-25,2015-06-16收修定稿
Identification of deep reservoir fluids based on basis pursuit inversion for elastic impedance
LIU Xiao-Jing, YIN Xing-Yao, WU Guo-Chen, ZONG Zhao-Yun
SchoolofGeosciences,ChinaUniversityofPetroleum(Huadong),Qingdao266580,China
AbstractFluid discrimination is an important technology for reservoir characterization in seismic exploration. Despite many years of studies on this tool, many problems remain unsolved. The conventional pre-stack inversion method is implemented based on three-parameter approximation. Usually, the density information is contained in three-parameter inversion. While for deep reservoirs, the maximum angle of incidence is not enough to invert the density information, and the low signal-to-noise ratio (SNR) of the data makes the inversion unstable. With the unstable pre-stack inversion, there will be more uncertainty in fluid identification. In order to stabilize the inversion and improve the accuracy of fluid identification for deep reservoirs, we present an identification method for deep reservoir fluids based on basis pursuit elastic impedance inversion.
KeywordsDeep reservoir; Two-term AVO approximation; Two-term elastic impedance; Basis pursuit; Fluid identification
刘晓晶, 印兴耀, 吴国忱等. 2016. 基于基追踪弹性阻抗反演的深部储层流体识别方法.地球物理学报,59(1):277-286,doi:10.6038/cjg20160123.
Liu X J, Yin X Y, Wu G C, et al. 2016. Identification of deep reservoir fluids based on basis pursuit inversion for elastic impedance.ChineseJ.Geophys. (in Chinese),59(1):277-286,doi:10.6038/cjg20160123.

