位场向下延拓的最小曲率方法
骆遥, 吴美平
1 国防科学技术大学 机电工程与自动化学院, 长沙 410073 2 中国国土资源航空物探遥感中心, 北京 100083
位场向下延拓的最小曲率方法
骆遥1, 2, 吴美平1
1 国防科学技术大学 机电工程与自动化学院, 长沙410073 2 中国国土资源航空物探遥感中心, 北京100083
摘要针对位场向下延拓的不适定性,我们将位场向下延拓视为向上延拓的反问题,提出以位场最小曲率作为约束条件来求解稳定的下延位场.我们将剖面位场向上延拓表达式用傅里叶矩阵的形式表示,以矩阵乘法形式给出延拓的表达式,同时向待反演的下延位场引入最小曲率约束,得到向下延拓的最小曲率解,并利用正交变换给出了更为简洁的频率域解.随后,利用Kronecker积将上述全部结果拓展至三维位场,给出了三维位场向下延拓的最小曲率解.此外,我们将位场数据的填充、扩充问题与向下延拓问题统筹考虑,提出一种新的向下延拓迭代格式,该算法面向实际资料处理需求、无须预扩充或填补数据.下延迭代时,对原始数据直接向下延拓,而空白部分利用上一次下延位场估计的上延值替代其空白值并对其向下延拓,直至获得最小曲率约束下稳定的向下延拓结果.同时,我们也讨论了利用改进L曲线和广义交叉验证(GCV)计算正则参数最优估计的问题.对理论模型和实际航空重力资料进行了向下延拓检验,处理结果表明位场向下延拓的最小曲率方法解能满足实际位场资料对向下延拓处理的需求,具有较高的下延精度.
关键词向下延拓; 最小曲率; 位场; 数据空白; 正则化
1引言
位场(重力场或地磁场)向下延拓可以从数学上拉近观测平面与场源间的距离,增强地质信息(改善信噪比),不仅在地球物理勘探中具有重要作用,还是利用重力场或地磁场特征进行导航的一项关键技术(胡小平等,2013),向下延拓技术在未爆军火探测等领域也有重要应用.位场向下延拓是经典的不适定问题(Blakely,1996;管志宁,2005),常规频率域位场下延强烈的表现出对数据高频部分的振荡,因而难于实际应用.尽管众多学者对位场向下延拓进行了大量细致的研究,但由于天然位场的频带之宽,各种向下延拓方法对不同资料适应性的差异很大.此外,几乎所有涉及频率域位场转换的研究中都假设输入的位场数据是纯粹的数学矩阵或向量,既要数据无空白,又要满足快速傅里叶变换(FFT)对数据长度的要求.实测位场资料很难满足上述条件,必须对资料空白部分进行填充、对数据进行扩充(扩边),这将直接关系到位场向下延拓的精度(王万银等,2009).数据的填充与扩充是实际位场资料延拓研究中难以回避的问题,需要加以解决.
正则化方法是求解不适定问题较完备且行之有效的方法.针对位场向下延拓的不适定性,我们以位场最小曲率作为约束条件求解稳定的下延位场,同时将位场数据的填充、扩充问题与向下延拓问题统筹考虑,提出一种将多种需求一并处理的向下延拓技术.具体研究中我们将位场向下延拓问题视为向上延拓的反问题,首先从二维位场剖面的向下延拓问题出发,将频率域向上延拓表达式用傅里叶变换矩阵的形式表示;利用矩阵乘法形式给出空间域向上延拓表达式的基础上,推导出向下延拓的频率域表达式及位场向下延拓的迭代解.同时,通过对下延位场引入最小曲率约束,给出了空间域向下延拓的最小曲率解,并最终通过正交变换给出更简洁的频率域解.随后,利用Kronecker积将上述结果拓展至三维位场,并给出了频率域三维位场向下延拓的最小曲率解.最后,我们讨论了频率域延拓中遇到的扩充数据、填补数据空白区等实际问题,给出了一种无须预扩充数据、填补数据空白的位场向下延拓技术,这对解决实际位场资料延拓问题具有重要意义.
2向下延拓技术方法
2.1二维位场延拓
位场解析延拓是典型的狄利克莱问题,根据重磁勘探教科书(如Blakely,1996;管志宁,2005;等),两个高度层的剖面二维位场满足
(1)
其中U(x,h)对应高高度层的位场,U(x,0)对应低高度层的位场,高度差h>0为常量.对其进行傅里叶变换,可以得到位场延拓的频率域表达式
FT[U(x,h)]=exp(-2πh|kx|)FT[U(x,0)],
(2)

(3)
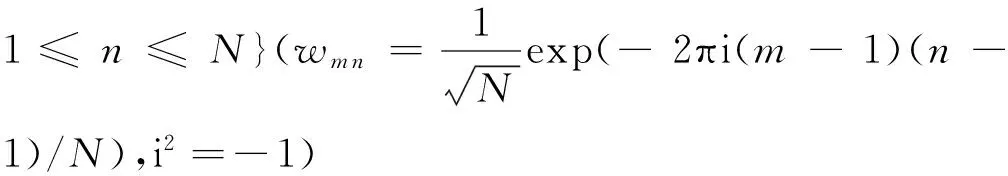
(4)
于是(2)式表达的位场延拓关系可写成矩阵形式,有
(5)
其中Uh=[U(1,h),…,U(n,h),…,U(N,h)]T,U0=[U(1,0),…,U(n,0),…,U(N,0)]T,U(n,·)对应离散序列在n(n=1,2,…,N)处的位场,ΛN=diag{exp(-2πh|kx1|),…,exp(-2πh|kxn|),…,exp(-2πh|kxN|)},kxn对应离散序列在n处的波数.若高高度位场Uh为观测位场,计算低高度位场U0的问题转化为求解目标函数
(6)
的极小化问题,其中‖·‖2表示L-2范数.该目标函数最小化的解为
(7)
其中上标T表示转置,即
(8)
将傅里叶变换矩阵用FT[·]表示,有
FT[U(x,0)]=exp(2πh|kx|)FT[U(x,h)].(9)
(9)
式就是位场向下延拓的频率域表达式.(6)式的极小化问题也可采用数值方法求解,如采用超松弛迭代法,有
(10)
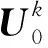

(11)
则
(12)将傅里叶变换矩阵用FT[·]表示,有
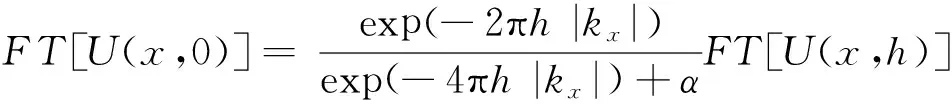
(13)即为通常意义下的位场向下延拓的正则化方法(栾文贵,1983;梁锦文,1989;Cooper,2004;陈生昌和肖鹏飞,2007).上述正则化方法的本质是引入了约束
(14)
即(12)或(13)式是目标函数
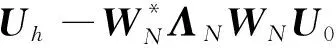
(15)
极小化的解.因此,位场向下延拓能否稳定的关键在于对下延位场施加的约束.实际上(15)式引入的约束仅体现模型最小,未反映位场本身的特性,并非“最优”.类似的,在位场反演中附加到场源的约束条件除模型最小外,还包括对模型的一阶偏导数,但将这类约束条件引入位场向下延拓问题中也不“恰当”,一阶偏导数最小是约束物性分布不存在间断,对位场本身而言仍不充分.
在处理位场资料插值或网格化问题时,Briggs(1974)引入了约束
(16)对离散数据进行网格化——即最小曲率网格化方法,Smith和Wessel(1990)曾对其进行改进.最小曲率网格化方法是目前位场资料网格化的标准方法.因此,利用最小曲率的方式约束位场向下延拓最为恰当,能够继承位场资料的网格化特征.对于剖面位场最小曲率的约束是
(17)
将其写成离散形式,有
(18)
其中下标N表示方阵阶数,该方阵具体为
(19)
为了减少频率域位场转换中Gibbs效应,DN算子采用了周期性边界条件.因此,在最小曲率条件约束下,求解下延位场的目标函数可表示为

在选择耕作方法时,综合考虑当季作物的效应及其对土壤肥力的影响。例如,免耕法具有提高播种质量、保持土壤水分、减少土壤侵蚀、降低生产成本等优点。但是采用免耕法,肥料只能施于土壤表层,肥料的利用率低,特别是有机肥料增肥土壤的作用大大降低。多点生产实践证明,不管什么类型的土壤,长期免耕必然造成土壤耕层变浅,影响作物根系下扎,不利于作物抗倒伏。要推广科学施肥技术,优化肥料运筹,改进施肥方法,发挥养分协同作用,提高肥料利用率,提升农作物产量。
(20)
其中α>0.对目标函数即(20)式极小化,有
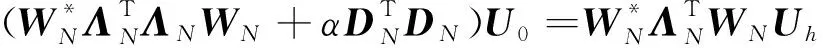
(21)
由于U0的左乘方阵是对角占优矩阵,可以直接求逆矩阵来解(21)式,也可以采用共轭梯度法求解(21)式.显而易见,随着观测数据的增多,求解该方程将变得极困难,不得不考虑类似反演问题中抽稀观测数据的做法(Foksetal., 2013).目前,航空磁测中单一测区覆盖面积最大达1.14×106km2(熊盛青等,2001),面对大数据处理量的实际情况,需考虑避免直接求解超大型方程组.我们考虑对(19)式算子进行正交分解(Strang, 1999),有
(22)
其中
(23)

故(21)式可记为
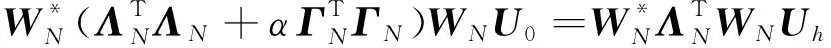
(24)
其解为
(25)
FT[U(x,0)]=
×FT[U(x,h)],
(26)
其中n=1,2,…,N是U(x,h)经离散傅里叶变换后对应序列中元素的序号.利用(26)式即可通过FFT直接计算在最小曲率条件约束下的下延位场,从而避免直接用(21)式在空间域中进行求解.
2.2三维位场延拓
类似的,重磁勘探教科书(Blakely,1996;管志宁,2005;等)也给了不同高度层间三维位场的关系,有U(x,y,h)=
对其进行傅里叶变换,可以得到位场延拓的频率域表达式
FT[U(x,y,h)]=
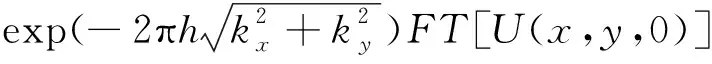
(28)
其中kx、ky对应频率域波数.按照前面的思路,可将(28)式表示成矩阵乘法的关系,但经二维离散傅里叶变换后的位场网格是M×N的矩阵,我们需要将FT[U(x,y,·)]表示成列向量形式,同时借助Kronecker积将二维傅里叶变换表示为矩阵乘法的形式.
设二维矩阵f={fm n∈f|1≤m≤M,1≤n≤N},经二维傅里叶变换得到的矩阵为F={Fm n∈F|1≤m≤M,1≤n≤N},将其表示为列向量形式,有vec(f)=[f11,f21,…,fM1,f12,f22,…,fM2,…,
f1N,f2N,…,fMN]T,
(29)
vec(F)=[F11,F21,…,FM1,F12,F22,…,FM2,…,
F1N,F2N,…,FMN]T,
(30)
其中vec(·)是将矩阵转为列向量的变换.于是离散傅里叶变换的矩阵表达为
(31)
其中⊗表示Kronecker积,有
(32)
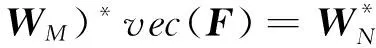
(33)
故(28)式可写成矩阵形式为
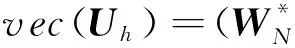
(34)
其中Uh、U0分别为高高度层和低高度层的位场网格,并以矩阵形式表示;

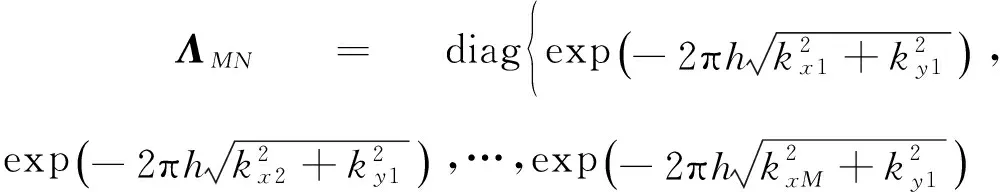
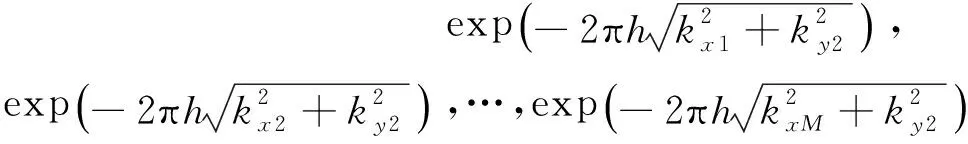
…,
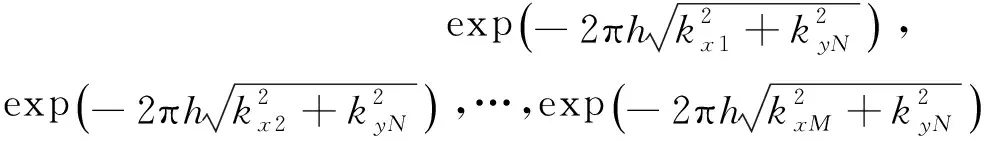

kxm表示位场经傅里叶变换后矩阵对应第m行处的波数,kyn表示对应第n列处的波数,显然对角阵ΛMN主对角线上元素构成的向量实际上是位场经傅里叶变换后矩阵所对应的频率域向上延拓因子的列向量变换.类似的,我们取目标函数
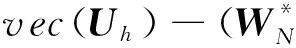
⊗WM)vec(U0)‖2,
(35)
其最小化的解为
(36)
即

⊗WMvec(Uh),
(37)
将傅里叶变换矩阵用FT[·]表示,有
(38)

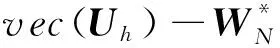
⊗WMvec(U0)‖2+α‖DMNvec(U0)‖2,
(39)
其中
(40)
对该目标函数极小化,有

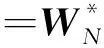
(41)
于是,下延位场计算可通过求解该方程获得.类似的物性反演中多采取共轭梯度法,但仍难以处理稍大的数据量,例如处理1024×1024大小的普通网格数据时,(41)式方程组的系数矩阵中元素个数就达1012量级,显然难以承受!出于实际考虑,我们利用频率域方法求解(41)式.


(42)
于是
(43)
其中
(44)
因此(41)式的解为
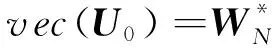
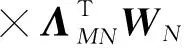
(45)
将傅里叶变换矩阵用FT[·]表示,有

(46)

其中m=1,2,…,M和n=1,2,…,N分别是U(x,y,h)经离散傅里叶变换后对应矩阵元素的行序号和列序号.(46)式即最小曲率约束下位场向下延拓的频率域解,该解与(41)式的空间域方法完全等效.
2.3正则参数选择
前面提出的基于最小曲率的位场向下延拓方法本质上属于正则化反演,正则参数的选择强烈地影响着向下延拓的结果,以往许多文献(栾文贵,1983;梁锦文,1989;Cooper,2004;陈生昌和肖鹏飞,2007)并没有专门对此进行讨论,其正则参数的选取多属经验性的.无论是二维位场还是三维位场其解析延拓都可表达为
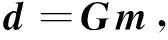
(47)
其中向量d表示观测位场,向量m表示下延位场,矩阵G表示向上延拓算子.求解下延位场就是求目标函数
(48)
的极小值问题,其中矩阵H表示前面的最小曲率约束算子(剖面数据时为DN,网格数据时为DMN).确定α的方法之一是L曲线法,但L曲线隅角的确定比较复杂,我们建议通过极小化泛函
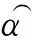
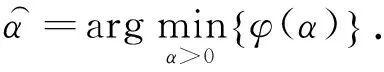
(50)
由于φ(α)能直接在频率域中求解,正则参数的确定是很容易的.除L曲线方法外,也可以利用广义交叉验证(GCV)方法确定正则化参数(Golub et al., 1979).广义交叉验证是通过极小化泛函
GCV(α)=n‖d-Gm(α)‖2/[n-Tr(A(α))]2,
(51)
确定正则参数,其中n是观测位场的数量,Tr(·)表示矩阵的迹,
(52)
(51)式的分子(不含n)同(49)式中乘法的第一项因子相同,是下延位场上延至原平面的恢复误差,可以用频率域上延算法快速计算.但对矩阵A的迹求解却较为困难,这里我们借鉴Garcia(2010)关于迹的处理,利用频率域与空间域的对应关系进行快速计算.对于剖面二维位场,有
(53)
对于网格三维位场,有
(54)

于是,通过(53)或(54)式可以快速计算(51)式所需的迹,从而获得对正则参数的最优估计,即
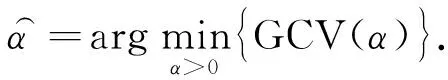
(55)
2.4数据填充与扩充处理
目前几乎所有的频率域位场转换都借助快速傅里叶变换(FFT)实现,而FFT对数据长度是有一定要求的,通常要求剖面数据的点数或网格数据的行、列数为合数,一般要求为以2为基(即2的自然数次幂).插值后的剖面位场或网格化后的位场通常难以满足上述要求,这就要求将剖面数据或网格数据向外扩充至FFT所要求的数据长度,即位场数据的扩充(扩边)问题.我们以FFT中最常见的2n为例,如果位场剖面的长度为1666个点,进行位场转换时就需要将剖面两端各扩充191个数据点,即扩充后数据长度为2048即211;再如位场网格的节点数为365×666,进行位场转换时就需要将网格首、末行的两端分别向外扩充73行和74行,再将扩充后网格的首、末列两端向外各扩充179列,扩充后的网格大小为512×1024即29×210.此外,由于多种因素某些区域缺乏实测位场数据,经过网格化后这些区域也无法形成相应的内插数据进而存在空白,位场转换中还要求将上述空白用合理的数据(称该数据为“假值”)进行填充(替代).填充与扩充中的间断现象将引起Gibbs效应,但许多理论研究者却并没有高度重视该问题.实际上,位场数据中空白值在航空磁测或航空重力测量中广泛存在却是不争的事实.测量中测线方向通常并非南北向或东西向,而是垂直于主地质构造走向,如果采用正网格(网格列方向为南北向)方式进行网格化势必产生大量数据空值(Zhang et al., 2012),即使采用斜网格(网格列方向为测线方向)方式进行网格化,也会因测区形状的不规则而产生一定数量的空值,有时还因特殊原因造成测区的部分数据缺失,部分历史航磁资料曾出现测区中间空白的情况.在航磁编图中数据空值问题更加突出,例如全国航磁编图中的位场转换中一个极重要的问题就是如何对网格空值进行假值填充处理,航磁编图数据在国境以外存在大量网格空值,即使利用国外磁测资料进行填充,但由于中国藏南地区、中国台湾海峡等尚存的航空磁测空白区,网格空值问题近乎无法避免!
除位场转换处理本身,数据填充与扩充处理是直接影响位场转换精度的重要因素,例如曾小牛等(2011)利用改进的积分迭代法处理重力资料时边界处的误差显著增大,明显是数据扩边不理想所致.由于某些位场转换研究本身就极富挑战性,很难再将填充与扩充处理统筹考虑,多数位场转换研究中仅讨论位场转换本身的精度,对数据空值填充或扩边的问题鲜有涉猎.姚长利等(2003)在低纬度化极时曾指出数据扩充对计算造成的影响不能忽视,但没给出进一步措施.张辉等(2009)结合正则化方法和维纳滤波方法研究波数域延拓算法时曾指出其算法存在边界效应问题,需引入扩边处理,但未对扩边算法进行研究.王万银等(2009)提出了用最小曲率方式对位场转换数据进行空值填补与扩边,其研究表明利用最小曲率方式进行数据扩充优于余弦方法,适于对位场数据扩充和填补空白.我们在前面的讨论中并没有涉及到数据填充与扩充处理,这就需要预先对位场数据中空值进行填补和扩充.似乎这样便解决位场下延中遇到的实际问题,但仔细考虑却存在矛盾,因为本文提出的向下延拓方法本身即基于最小曲率方式,而最小曲率方法却多用于对未知位场的插值处理(Briggs, 1974;Smith and Wessel, 1990),这似乎表明没有必要单独对数据进行填充和扩充处理.
基于解决位场数据存在假值与扩边问题的实际需求,结合最小曲率方法的特性,我们将前面所述的位场向下延拓方法进一步扩展.这里我们借鉴了Garcia(2010)对数据空值估计的思想,提出下延处理中对非空数据直接使用,而空白部分则利用上一次下延位场(估计)的上延值代替并进行迭代,具体的计算格式为
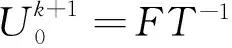

(56)
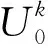
3理论模型计算
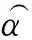

图1 二维重力模型及其向下延拓结果对比
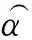

图2 地面(h=0 km)和高空(h=1 km)处的模型磁异常
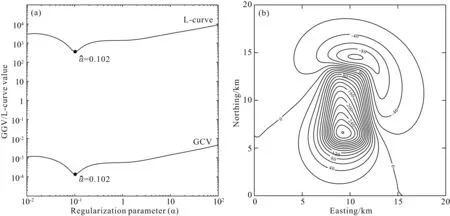
图3 正则参数曲线(a)与向下延拓结果(b)
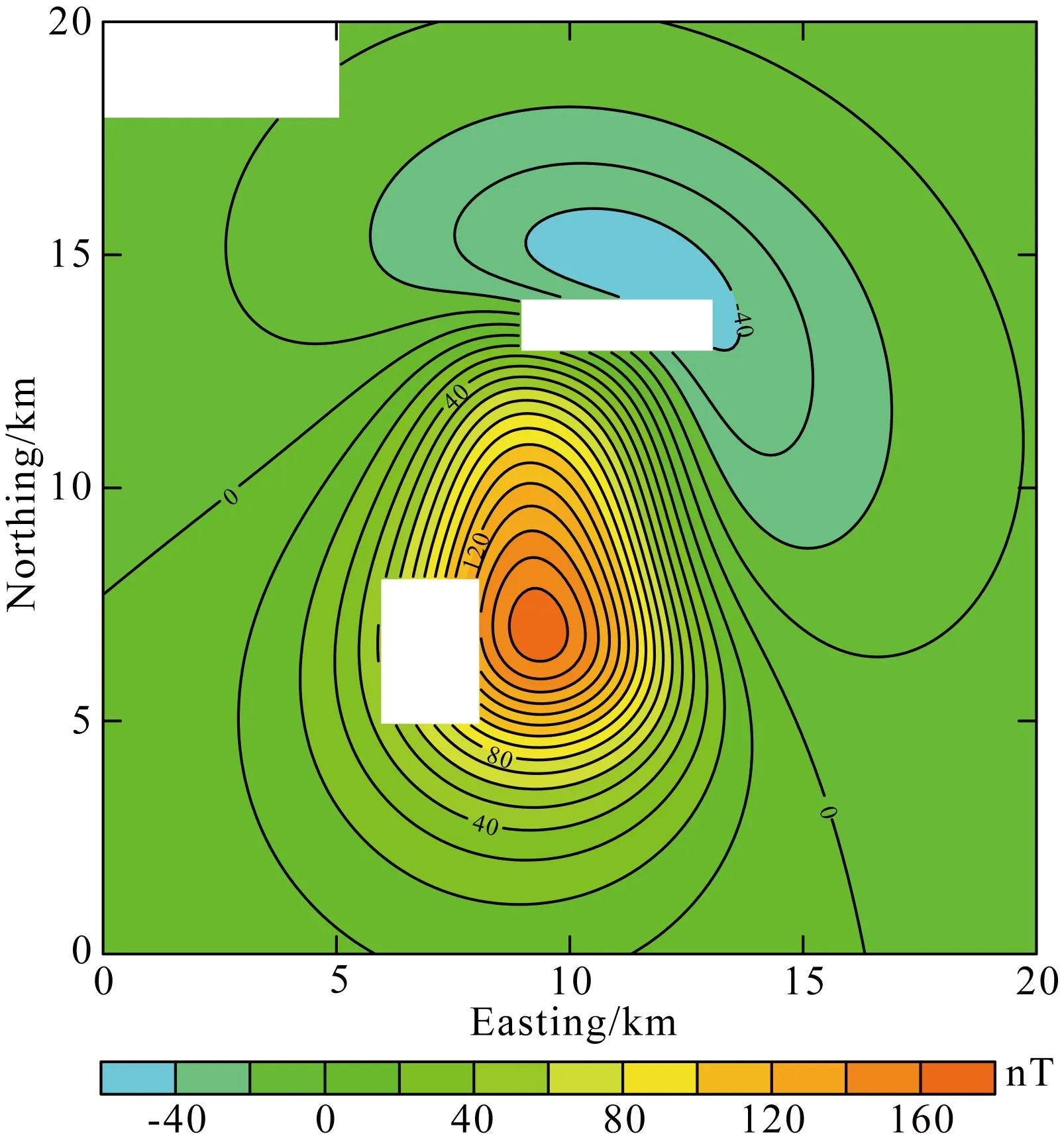
图4 高空(h=1 km)处的模型磁异常(白色区域为三处数据空白区)
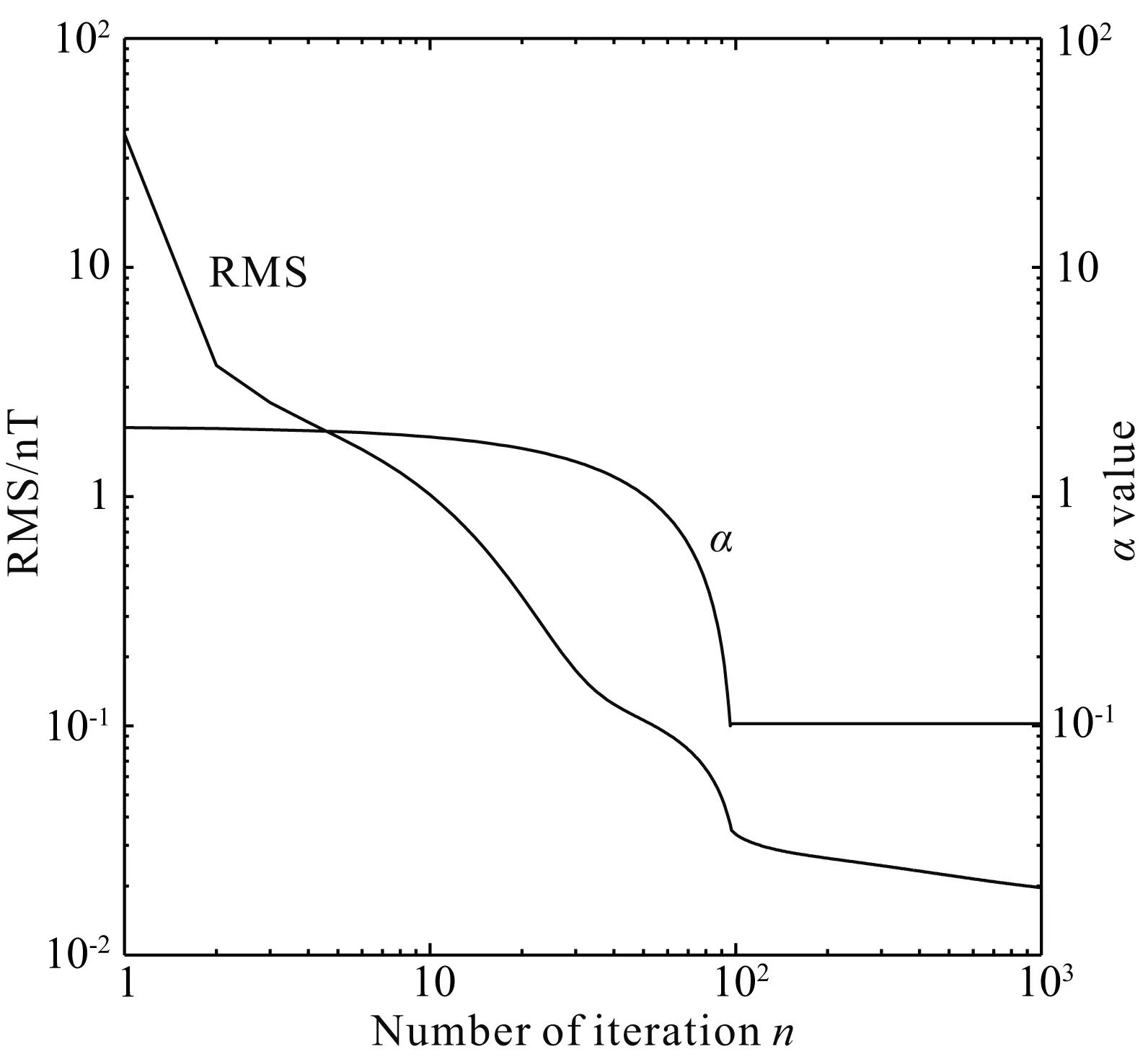
图6 迭代过程使用的正则参数及相应迭代步的均方误差
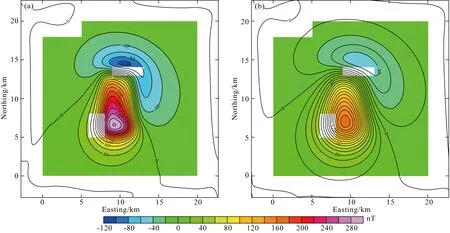
图5 向下延拓结果(a)及其上延恢复的观测异常(b)其中(a)和(b)对应的理论模型异常数据以等值线的彩色填充形式叠加作为比照.
4实际资料处理
为了检验位场最小曲率向下延拓方法在实际数据处理中的实用性,我们采用美国地质勘探局(USGS)2006年在阿富汗实测的航空重力资料进行数据处理检验.该航空重力测量数据经各项处理并最终归算至离地7000 m的高度,形成网格距为1 km的布格重力异常.图7给出了布格重力异常图(等值线间隔10 mGal),其中角图中蓝色区块为航空重力测量覆盖范围,红点为1966—1967年地面重力测量点.由图7可知该测区极不规则且不同区块测线方向不同(测线间距也有所不同),这些特征是航空物探作业中的典型特点,但多数向下延拓文献却刻意回避这些特点,而是将类似情况的数据裁剪成特殊的无空值矩形网格进行处理,以避免数据填充或扩充(扩边)问题.我们将图7的布格重力异常延拓至地面(下延距离7000 m),由于图7的网格含有(大量)空白数据,这里采用(56)式给出的迭代格式进行求解(迭代过程中正则参数逐渐缩小并最终等于预估值α=0.65),图8给出了最终下延至地面的布格重力异常(等值线间隔10 mGal).可以看出,向下延拓7000 m后得到的重力异常(图8)没有出现虚假的振荡,在保持原始异常变化趋势的同时增强了局部异常.我们将图8的布格重力异常同地面布格重力异常进行比较,二者的外符合精度(郭志宏等, 2008)为7.5 mGal,反映二者差异较大,但却难以反映延拓处理的精度.USGS为了编图的需要将地面布格异常归算至距地面7000 m的高空,归算后的布格异常同航空重力异常比较,二者的外符合精度也仅为6.4 mGal,可见该地区的地面重力资料和航空重力资料本身符合的就不甚理想,这也是向下延拓至地面的布格异常同地面实测结果相差较大的原因.如果忽略二者间资料本身的差异,向下延拓引起的误差可近视为两种外符合精度之差即1.1 mGal,相对于下延7000 m(7倍网格距)而言,延拓精度是相当可观的.此外,我们将图8的布格异常上延恢复至原高度比较其与图7的差异,二者相差小于0.36 mGal的网格点占99%,其差值的均方差仅0.1 mGal,也进一步证明了向下延拓的数值精度.

图7 航空布格重力异常数据(归算离地高度7 km)
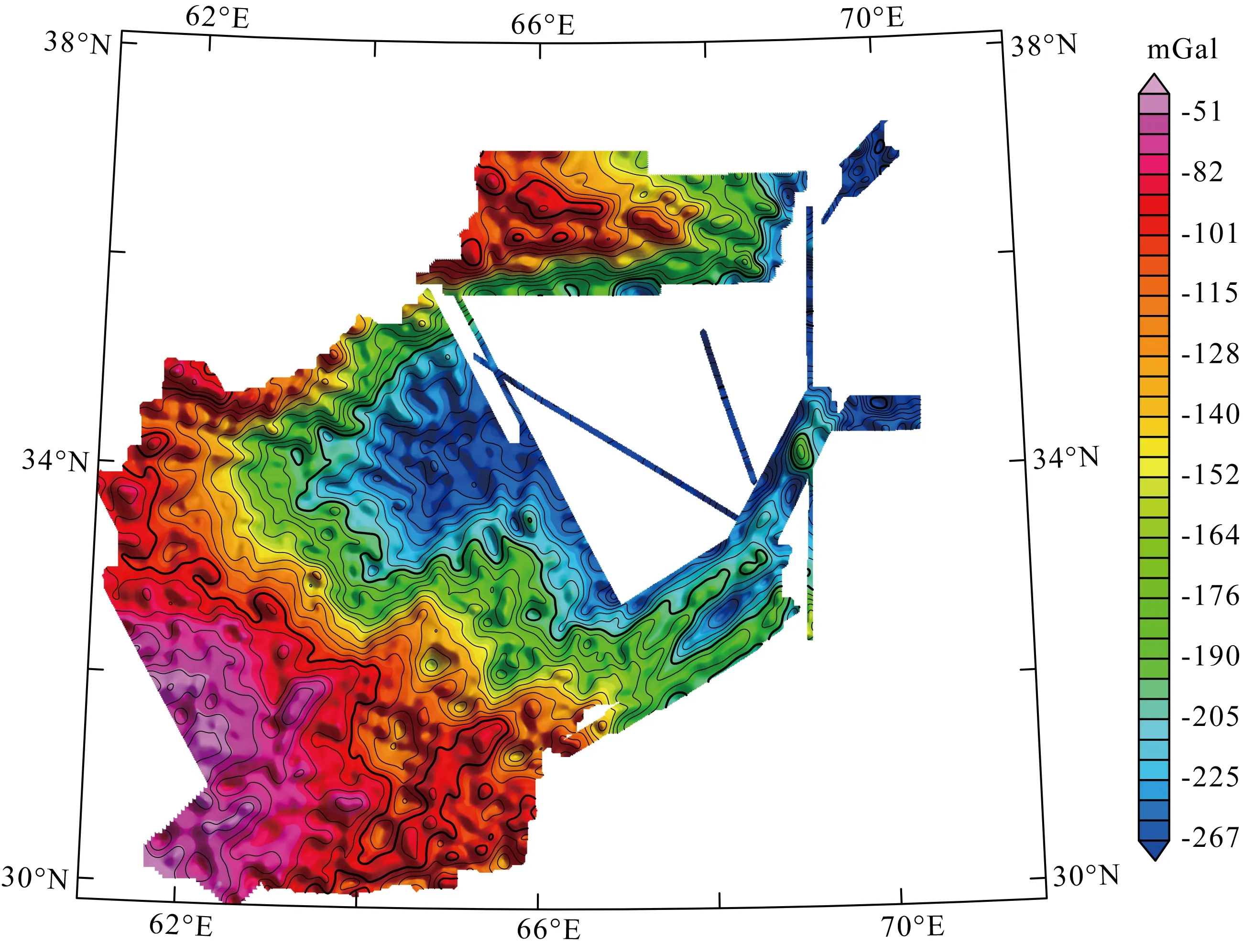
图8 向下延拓至地面的航空布格重力异常
5结论
我们将位场向下延拓视为向上延拓处理的反问题,并以位场最小曲率条件为正则化约束,反演位场数据向下延拓的最小曲率解.由于使用了傅里叶变换矩阵,我们提出的向下延拓方法既可以在空间域求解,也可在频率域通过快速傅里叶变换直接求解.此外,我们讨论了频率域延拓中遇到的扩充数据、填补数据空白区两项实际问题,给出了无须预扩充数据、填补数据空白的位场向下延拓算法.针对我们提出的频率域向下延拓的最小曲率解,我们分别利用二维重力模型和三维磁异常模型进行了检验,并特别针对三维位场数据中含数据空白的情况进行了专门的检验,无论是向下延拓的数值精度还是对空白区的恢复都取得了良好的理论模型效果.同时,我们选取实测的航空重力资料进行向下延拓处理.该测区极不规则,并含有大块的数据空白区域,甚至个别数据仅由单条测线网格化而来.在未对该资料进行填充、扩充等预处理情况下直接将其向下延拓至地面,处理结果表明该方法具有较高的向下延拓精度,可在实际位场资料处理应用中发挥积极作用.
致谢图7使用了美国地质勘探局(USGS)公布的航空重力数据和地面重力数据,在此表示感谢.
References
Arisoy M Ö, Dikmen Ü. 2011. Potensoft: MATLAB-based software for potential field data processing, modeling and mapping.Computers&Geosciences, 37(7): 935-942, doi: 10.1016/j.cageo.2011.02.008.Blakely R J. 1996. Potential Theory in Gravity and Magnetic Applications. New York: Cambridge University Press.
Briggs I C. 1974. Machine contouring using minimum curvature.Geophysics, 39(1): 39-48, doi: 10.1190/1.1440410.
Chen S C, Xiao P F. 2007. Wavenumber domain generalized inverse algorithm for potential field downward continuation.ChineseJ.Geophys. (in Chinese), 50(6): 1816-1822.
Cooper G. 2004. The stable downward continuation of potential field data.ExplorationGeophysics, 35(4):260-265, doi: 10.1071/EG04260.
Cooper G R J, Cowan D R. 2005. Differential reduction to the pole.Computers&Geosciences, 31(8): 989-999, doi: 10.1016/j.cageo.2005.02.005.
Foks N L, Krahenbuhl R, Li Y G. 2013. Adaptive sampling of potential-field data: A direct approach to compressive inversion.Geophysics, 79(1): IM1-IM9, doi: 10.1190/GEO2013-0087.1.
Gao Y W, Luo Y, Wen W. 2012. The compensation method for downward continuation of potential field from horizontal plane and its application.ChineseJ.Geophys. (in Chinese), 55(8): 2747-2756, doi: 10.6038/j.issn.0001-5733.2012.08.026.
Garcia D. 2010. Robust smoothing of gridded data in one and higher dimensions with missing values.ComputationalStatistics&DataAnalysis, 54(4): 1167-1178, doi: 10.1016/j.csda.2009.09.020.Golub G H, Heath M, Wahba G. 1979. Generalized cross-validation as a method for choosing a good ridge parameter.Technometrics, 21(2): 215-223, doi: 10.1080/00401706.1979.10489751.
Guan Z N. 2005. Magnetic Field and Magnetic Exploration (in Chinese). Beijing: Geological Publishing House.
Guo Z H, Guan Z N, Xiong S Q. 2004. Cuboid ΔTand its gradient forward theoretical expressions without analytic odd points.ChineseJ.Geophys. (in Chinese), 47(6): 1131-1138.
Guo Z H, Xiong S Q, Zhou J X, et al. 2008. The research on quality evaluation method of test repeat lines in airborne gravity survey.ChineseJ.Geophys. (in Chinese), 51(5): 1538-1543.
Hu X P, Wu M P, Mu H, et al. 2013. Technologies on Underwater Geomagnetic Field Navigation (in Chinese). Beijing: National Defense Industry Press.
Liang J W. 1989. Downward continuation of regularization methods for potential fields.ChineseJ.Geophys. (ActaGeophysicaSinica) (in Chinese), 32(5): 600-608.Liu D J, Hong T Q, Jia Z H, et al. 2009. Wave number domain iteration method for downward continuation of potential fields and its convergence.ChineseJ.Geophys. (in Chinese), 52(6): 1599-1605, doi: 10.3969/j.issn.0001-5733.2009.06.022.Luan W G. 1983. The stabilized algorithm of the analytic continuation for the potential field.ChineseJ.Geophys. (ActaGeophysicaSinica) (in Chinese), 26(3): 263-274.Luo Y, Yao C L. 2007. Theoretical study on cuboid magnetic field and its gradient expression without analytic singular point.OilGeophysicalProspecting(in Chinese), 42(6): 714-719.
Smith W H F, Wessel P. 1990. Gridding with continuous curvature splines in tension.Geophysics, 55(3): 293-305, doi: 10.1190/1.1442837.
Strang G. 1999. The discrete cosine transform.SIAMReview, 41(1): 135-147, doi: 10.1137/S0036144598336745.
Wang W Y, Qiu Z Y, Liu J L, et al. 2009. The research to the extending edge and interpolation based on the minimum curvature method in potential field data processing.ProgressinGeophys. (in Chinese), 24(4): 1327-1338, doi: 10.3969/j.issn.1004-2903.2009.04.022.
Xiong S Q, Zhou F H, Yao Z X, et al. 2001. Aeromagnetic Survey in Central and Western Qinghai-Tibet Plateau (in Chinese). Beijing: Geological Publishing House.
Xu S Z, Yang J Y, Yang C F, et al. 2007. The iteration method for downward continuation of a potential field from a horizontal plane.GeophysicalProspecting, 55(6): 883-889, doi: 10.1111/j.1365-2478.2007.00634.x.Yao C L, Guan Z N, Gao D Z, et al. 2003. Reduction-to-the-pole of magnetic anomalies at low latitude with suppression filter.ChineseJ.Geophys. (in Chinese), 46(5): 690-696.
Yao C L, Li H W, Zheng Y M, et al. 2012. Research on iteration method using in potential field transformations.ChineseJ.Geophys. (in Chinese), 55(6): 2062-2078, doi: 10.6038/j.issn.0001-5733.2012.06.028.Zhang C, Yao C L, Xie Y M, et al. 2012. Reduction of distortion and improvement of efficiency for gridding of scattered gravity and magnetic data.AppliedGeophysics, 9(4): 378-390, doi: 10.1007/s11770-012-0349-x. Zhang H, Chen L W, Ren Z X, et al. 2009. Analysis on convergence of
iteration method for potential fields downward continuation and research on robust downward continuation method.ChineseJ.Geophys. (in Chinese), 52(4): 1107-1113, doi: 10.3969/j.issn.0001-5733.2009.04.028.
Zheng X N, Li X H, Liu D Z, et al. 2001. Regularization analysis of integral iteration method and the choice of its optimal step-length.ChineseJ.Geophys. (in Chinese), 54(11): 2943-2950, doi: 10.3969/j.issn.0001-5733.2011.11.024.
附中文参考文献
陈生昌, 肖鹏飞. 2007. 位场向下延拓的波数域广义逆算法. 地球物理学, 50(6): 1816-1822.
高玉文, 骆遥, 文武. 2012. 补偿向下延拓方法研究及应用. 地球物理学报, 55(8): 2747-2756, doi: 10.6038/j.issn.0001-5733.2012.08.026.
管志宁. 2005. 地磁场与磁力勘探. 北京: 地质出版社.
郭志宏, 管志宁, 熊盛青. 2004. 长方体ΔT场及其梯度场无解析奇点理论表达式. 地球物理学报, 47(6): 1131-1138.
郭志宏, 熊盛青, 周坚鑫等. 2008. 航空重力重复线测试数据质量评价方法研究. 地球物理学报, 51(5): 1538-1543.
胡小平, 吴美平, 穆华等. 2013. 水下地磁导航技术. 北京: 国防工业出版社.
梁锦文. 1989. 位场向下延拓的正则化方法. 地球物理学报, 32(5): 600-608.
刘东甲, 洪天求, 贾志海等. 2009. 位场向下延拓的波数域迭代法及其收敛性. 地球物理学报, 52(6): 1599-1605, doi: 10.3969/j.issn.0001-5733.2009.06.022.
栾文贵. 1983. 场位解析延拓的稳定化算法. 地球物理学报, 26(3): 263-274.
骆遥, 姚长利. 2007. 长方体磁场及其梯度无解析奇点表达式理论研究. 石油地球物理勘探, 42(6): 714-719.
王万银, 邱之云, 刘金兰等. 2009. 位场数据处理中的最小曲率扩边和补空方法研究. 地球物理学进展, 24(4): 1327-1338, doi: 10.3969/j.issn.1004-2903.2009.04.022.
熊盛青, 周伏洪, 姚正煦等. 2001. 青藏高原中西部航磁调查. 北京: 地质出版社.
姚长利, 管志宁, 高德章等. 2003. 低纬度磁异常化极方法——压制因子法. 地球物理学报, 46(5): 690-696.
姚长利, 李宏伟, 郑元满等. 2012. 重磁位场转换计算中迭代法的综合分析与研究. 地球物理学报, 55(6): 2062-2078, doi: 10.6038/j.issn.0001-5733.2012.06.028.
张辉, 陈龙伟, 任治新等. 2009. 位场向下延拓迭代法收敛性分析及稳健向下延拓方法研究. 地球物理学报, 52(4): 1107-1113, doi: 10.3969/j.issn.0001-5733.2009.04.028.
曾小牛, 李夕海, 刘代志等. 2011. 积分迭代法的正则性分析及其最优步长的选择. 地球物理学报, 54(11): 2943-2950, doi: 10.3969/j.issn.0001-5733.2011.11.024.
(本文编辑何燕)
基金项目国家自然科学基金(61174206)、国家高技术研究发展计划(863计划)(2011AA060501,2013AA063901,2013AA063905)和中国地质调查(1212011120189)项目资助.
作者简介骆遥,男,1982年生,博士研究生,高级工程师,主要从事地球物理探测等相关技术研究.E-mail:geophy@vip.qq.com
doi:10.6038/cjg20160120 中图分类号P631
收稿日期2015-01-22,2015-12-09收修定稿
Minimum curvature method for downward continuation of potential field data
LUO Yao1, 2, WU Mei-Ping1
1CollegeofMechatronicsEngineeringandAutomation,NationalUniversityofDefenseTechnology,Changsha410073,China2ChinaAeroGeophysicalSurveyandRemoteSensingCenterforLandandResources,Beijing100083,China
AbstractDownward continuation calculates the potential field that is closer to the source of anomalies is a powerful but unstable tool in data processing. To obtain a reasonable downward continued result, we formulate the downward continuation process as an inverse problem of upward continuation, and introduce a discretized smoothing continuous curvature spline regularization approach to solve it. The proposed method, which is based on the discrete Fourier transform (DFT) matrix, allows robust smoothing of downward continued field data. In the study, we formulate the upward continuation of 2-D potential field data as matrix multiplication in the form d=Gm represented by DFT matrix. Then, the inverse problem is formulated as minimizing a total objective function consisting of total squared curvature of downward continued field data and data misfit. Because the number of data is often large, calculating the matrix equation is a major computational load of the downward continuation. We greatly simplify and solve it by means of the DFT. Then we extend the method to 3-D potential field by using the Kronecker product, and obtain the minimum curvature solution of downward continued field data in the frequency domain. As the results of downward continuation are strongly influenced by the smoothing parameter, automatic choice of the amount of regularization parameter is carried out using the method of L-curve and generalized cross validation (GCV). In addition, we consider the problems on data missing and grid expansion in the downward continuation of potential field. An iterative robust scheme of downward continuation is then proposed to deal with data expansion or replacing dummy values with interpolated values. To test the performance of the method, we employ the synthetic and real airborne gravity data for downward continuation. Data processing results on both the synthetic and real data confirm that the performance of the proposed technique can satisfy the need of real data processing for downward continuation of the potential field.
KeywordsDownward continuation; Minimum curvature; Potential field; Missing data; Regularization
骆遥,吴美平. 2016. 位场向下延拓的最小曲率方法.地球物理学报,59(1):240-251,doi:10.6038/cjg20160120.
Luo Y, Wu M P. 2016. Minimum curvature method for downward continuation of potential field data.ChineseJ.Geophys. (in Chinese),59(1):240-251,doi:10.6038/cjg20160120.

