S变换相对谱熵及其在液压泵退化状态识别中的应用
王余奎,李洪儒,黄之杰,赵徐成(.空军勤务学院,江苏徐州000;.军械工程学院,河北石家庄050003)
S变换相对谱熵及其在液压泵退化状态识别中的应用
王余奎1,2,李洪儒2,黄之杰1,赵徐成1
(1.空军勤务学院,江苏徐州221000;2.军械工程学院,河北石家庄050003)
摘要:为更好地表征液压泵的退化状态,对液压泵退化特征提取方法和退化状态识别方法进行研究。基于S变换分析非平稳信号的优异能力以及相对熵较好表征振动信号概率分布差异的特性,提出S变换相对谱熵的液压泵退化特征提取方法,对液压泵仿真信号分析结果验证了所提出的S变换相对能谱熵和S变换相对奇异谱熵作为退化特征的有效性和可行性。将两个特征指标组成退化特征向量,对滑靴磨损和松靴故障模式下不同故障程度的液压泵振动信号进行分析,进一步验证所提出的特征指标作为液压泵退化特征的有效性。将加权灰关联法用于液压泵退化状态识别,建立了液压泵的标准退化模式矩阵,对两种故障模式下液压泵待检测样本的退化特征向量和标准模式矩阵做加权灰关联分析,根据灰关联度的大小判定液压泵的退化状态,结果验证了所提出方法的良好性能。
关键词:兵器科学与技术;液压泵;退化状态识别;S变换;相对谱熵;加权灰关联分析
0 引言
液压系统作为某型导弹发射车的重要组成部分,在作战中起着至关重要的作用。液压泵作为该液压泵系统的动力源,其性能好坏影响着整个液压系统功能的实现和该导弹发射车战斗力的生成[1]。此外,随着维修理论和相关技术的发展,以故障预测技术为核心的基于状态的维修越来越受大家重视[2],而基于状态的维修需要对其故障程度和发展趋势进行估计。但现有的液压泵振动信号分析方法多是集中在故障类型识别和故障位置判定上[3]。因此通过对液压泵退化状态识别方法进行研究,从而对液压泵和整个液压泵系统的性能进行判定,对保障导弹发射车战斗力生成具有重要意义[4]。
退化特征提取是退化状态识别的关键环节,所提取特征性能的好坏对退化状态识别结果影响很大[5]。在机械设备出现某种故障时,随着故障程度的加深,其能量会越来越集中在故障特征频率[6],这样振动信号的概率分布也会随着故障程度地加深而变化[7]。相对熵是一种测量两种概率分布偏差的指标,两种概率分布间相对熵越小说明其分布越一致,反之亦然[8]。基于以上分析,本文拟采用正常状态下振动信号的概率分布为标准,计算不同程度故障状态下振动信号与正常状态振动信号的相对熵,并将相对熵作为反应液压泵故障程度的指标。相对熵的计算需要以振动信号时频分析为基础,在液压泵出现故障时其振动信号表现出较强的非平稳特性,因此有必要采用非平稳分析方法对振动信号进行时频分析[9]。在常用的时频分析方法中,S变换不仅能够保持信号的绝对相位信息,而且具有多分辨率特性,可以保证良好的分辨率,弥补了小波变换(WT)缺乏信号相位信息的不足和短时傅里叶变换(STFT)时频分辨率固定的缺陷[10-12]。本文将S变换算法和相对熵原理相结合,提出了基于S变换相对谱熵的液压泵退化特征提取方法,定义了S变换相对能谱熵和S变换相对奇异谱熵的概念,通过对仿真信号分析,验证提出方法的合理性和有效性。通过对液压泵实测信号分析进一步验证所提出退化特征的性能,并采用加权灰关联分析法实现液压泵的退化状态识别。
1 S变换原理
对于一维信号x(t),其连续S变换S(τ,f)定义[12]为
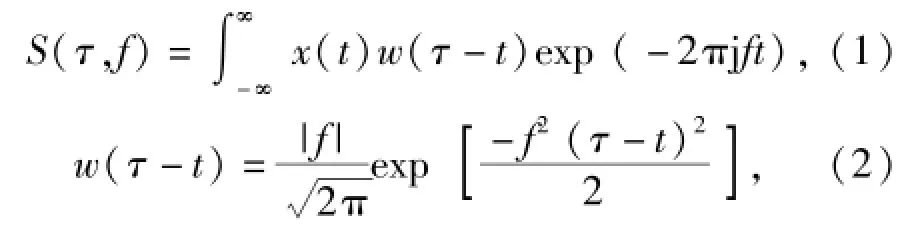
式中:w(τ-t,f)为高斯窗函数;τ是调整高斯窗在时间轴位置的参数;f是频率;j是虚数的单位。由(1)式和(2)式可知,S变换是一种特殊的STFT,其窗函数为高斯窗,且窗宽与信号频率f呈反比[10]。所以,S变换在分析信号的低频成分时具有更高的频率分辨率,在分析信号的高频段时具有更高的时间分辨率[12]。
假设时间序列{x[kT],k=0,2,3,…,N-1}是x(t)的离散时间序列,N是采样点数,T为采样间隔,x[kT]的离散傅里叶变换为X[k/NT],则该时间序列的离散S变换[12]可以通过(3)式实现:
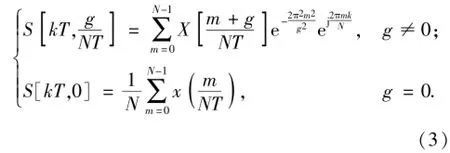
x[kT]的离散S变换结果是一个复时频矩阵,矩阵的列是采样时间,矩阵的行是离散频率,第g(g=1,2,…,G)行的频率为
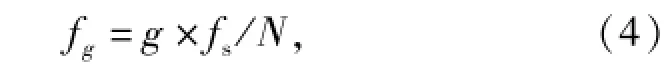
式中:fs是信号的采样频率。
2 S变换相对谱熵的提出
S变换是一种具有多分辨率特性的振动信号时频分析方法,对信号进行S变换就是在不同的频率下对振动信号进行划分。对正常液压泵振动信号进行S变换,其能量在各频带的分布具有确定性。而当液压泵出现某种故障时,随着故障程度的加深,其振动信号概率分布偏离正常振动信号概率分布的程度也会随之而变化。基于以上分析,并结合相对熵的概念提出了S变换相对谱熵的概念。
2.1S变换相对能谱熵的定义
对于确定程度的某种故障,假设采集了M个样本,则该故障样本xi(t)(i=1,2,…,M,t=0,1,2,…,N-1)与正常信号xb(t)(t=0,1,2,…,N-1)的相对能谱熵可以采用以下步骤计算:
1)对正常样本和采集的故障样本进行S变换,结果分别为Sb(t,f)和Si(t,f)(i=1,2,3,…,M);
2)计算正常样本和故障样本xi(t)在频率fg下的能量:

计算所有频率下的能量,可以得到正常样本和故障样本xi(t)的S变换能量谱和,采用同样的方法求取所有样本的S变换能量谱。
3)计算所有样本在频率fg下的能量和:
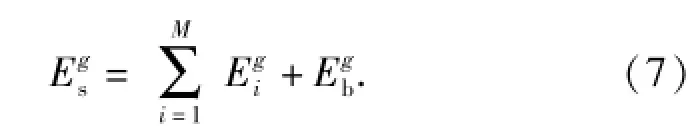
4)计算频率fg下xb(t)和xi(t)能量占总能量的百分比:

5)根据相对熵的原理,定义故障样本i与正常样本的S变换相对能谱熵(RNE)为
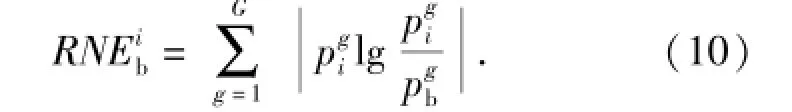
根据S变换相对能谱熵的定义知,RNEib能够表征故障状态样本i与正常样本能量概率分布之间的差异,相对能谱熵值越大,故障样本与正常样本间的差别越大,故障程度越深;反之亦然。
2.2S变换相对奇异谱熵的定义
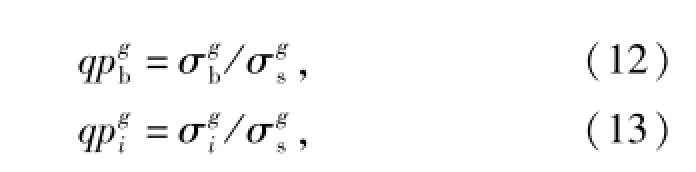
将S变换算法、奇异值分解算法和相对熵概念结合提出了S变换相对奇异谱熵的概念。对于正常样本,首先对其进行S变换,得到其S变换时频谱Sb(t,f).对Sb(t,f)进行奇异值分解,可以得到其奇异值谱。对于确定程度的某种故障,采集了M个样本,求取每个样本的奇异值谱,样本i的奇异值谱可以表示为。结合相对熵的概念,定义故障样本i与正常样本的S变换相对奇异谱熵(RQE)为

2.3仿真分析
为了验证所提出RNE、RQE表征液压泵故障退化的能力,采用仿真信号模拟液压泵的故障退化过程。设置仿真信号[13]为
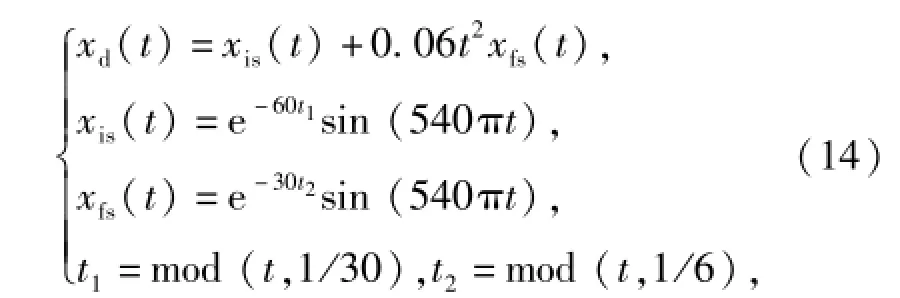
式中:xis(t)模拟液压泵振动信号中的固有冲击成分,即正常信号,其波形图如图1所示;xfs(t)模拟液压泵故障引起的冲击成分;0.06t2xfs(t)模拟液压泵故障加深的过程。设置xd(t)的采样点数为N= 40 960,采样频率为1 024 Hz,图2是其时域波形图。
图1 正常液压泵仿真信号波形图Fig.1 Simulation signal of normal hydraulic pump
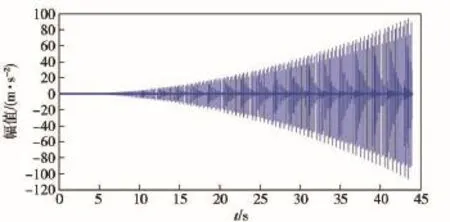
图2 液压泵故障退化仿真信号波形图Fig.2 Fault degradation simulation signal of hydraulic pump
首先,将xd(t)等分为10组并按顺序标记,每段数据点数为4 096,采用这样的10组数据来近似模拟液压泵故障不断加深的过程[14]。以正常信号为标准,计算以上10组数据与正常信号的RNE和RQE,结果如图3所示。由图3可知:所提出的两个特征指标都随着故障程度的加深而变大,说明随着故障程度的加深,故障信号的概率分布偏离正常信号概率分布的程度越来越大,仿真信号的分析结果表明所提出的两个指标与故障退化的趋势关联性较好。因此,本文选取以上两个参数作为液压泵的退化特征来表征液压泵的故障程度。

图3 仿真信号S变换相对谱熵Fig.3 ST relative spectrum entropy of simulation signal
3 基于S变换相对谱熵的液压泵退化状态识别
3.1液压泵退化状态识别策略
灰关联分析是一种数据到数据的映射,它基于灰色系统的灰色过程,是动态过程发展态势的量化。灰关联分析可以描述系统发展过程中因素间的相对变化情况,如果两个因素在发展变化过程中的变化基本一致,则二者的灰色关联度大;反之亦然。液压泵的性能退化过程是一个灰色过程,且S变换相对谱熵描述的是在故障发展过程中,故障信号概率分布与正常信号概率分布的相对变化情况。因此,采用S变换相对谱熵作为退化特征,并采用灰关联分析进一步实现故障退化过程中两个概率分布差异的变化趋势具有一定的理论基础。但是灰关联分析将不同的故障特征赋予同样的权重,没有考虑不同的故障特征具有不同重要程度的问题,从而导致其分析结果的准确性和可靠性不高。针对该问题,有学者提出了加权灰关联分析法[15],很好的克服了以上问题。基于以上分析,本文提出了基于S变换相对谱熵和加权灰关联分析的液压泵退化状态识别方法。液压泵退化状态识别的策略如图4所示。
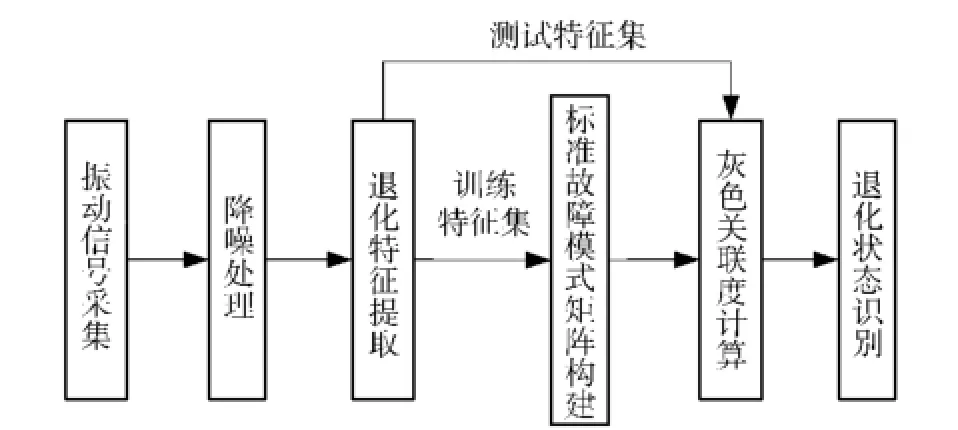
图4 液压泵退化状态识别策略Fig.4 Identification strategy of hydraulic pump degradation state
3.2振动信号采集

图5 液压泵试验台Fig.5 Test bench of hydraulic pump
实测液压泵振动信号采自液压泵试验台[13],如图5所示。液压泵型号为L10VSO28DFR,其额定转速为1480 r/min,采用型号为YPT-280M-2的变频电机驱动。选用美国NI公司的603C01型加速度传感器,与液压泵壳体进行刚性连接,如图6所示。本文研究主要对液压泵出现松靴或滑靴磨损单故障时的振动信号进行分析。为获得较为真实的振动信号,液压泵退化状态采用装备检修时换下的不同程度松靴和滑靴磨损的柱塞代替正常柱塞的方式模拟。为界定松靴故障的程度,定义松靴度为滑靴与柱塞间能够发生的最大轴向位移量。采用游标卡尺测量试验中所用的5个松靴柱塞的松靴度分别为:0.11 mm、0.18 mm、0.29 mm、0.41 mm和0.54 mm.为界定滑靴磨损的程度,定义滑靴磨损度为滑靴靴帽磨损的值。试验中所用4个滑靴磨损柱塞的滑靴磨损度分别为:0.1 mm、0.14 mm、0.20 mm和0.27 mm.采用美国NI公司的cDAQ-9171型测量与试验系统采集不同状态下的液压泵振动信号各200组,每组采样点数为4 096,数据采样频率为50 kHz,采样间隔为30 s,试验过程中试验台主溢流阀压力为10 MPa.电机转速为其额定转速,为了避免电机转速波动带来的影响,试验中数据采集均在电机转速稳定后进行。所采集部分振动信号如图7所示。

图6 传感器的安装Fig.6 Layout of sensors
3.3液压泵退化特征集提取
3.3.1正常信号平滑处理
从正常信号中选取较平稳的一组样本作为相对谱熵计算的标准信号,为了减小振动随机性对相对谱熵的影响,研究中采用7点滑移平均法[16]处理标准信号,7点滑移平均按(15)式进行。平滑处理后标准信号的时域波形如图8所示。
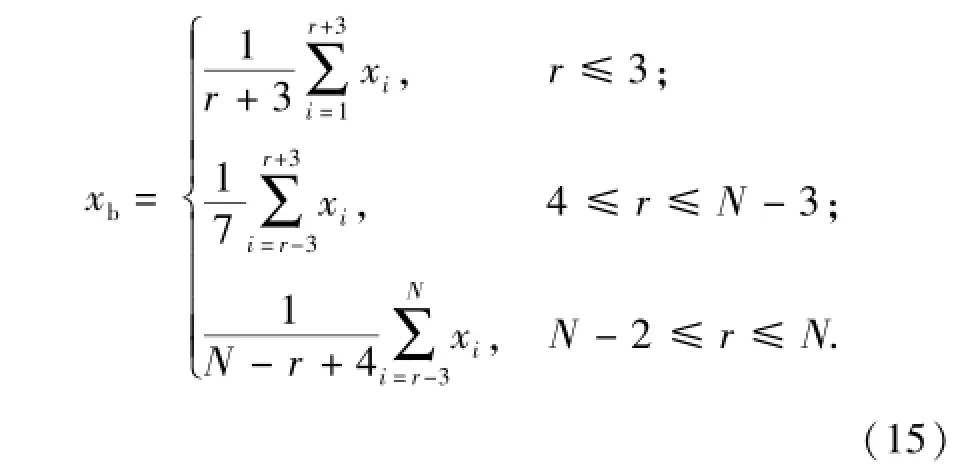
3.3.2退化特征提取
将正常状态作为退化状态的一种特殊情况,则松靴故障共有6种退化状态,滑靴磨损故障共有5种退化状态。对于松靴故障,将正常状态标记为退化状态0,从松靴度为0.11 mm到松靴度为0.54 mm 5种状态分别记为退化状态1~退化状态5;采用同样的方式将滑靴磨损故障的退化状态记为退化状态0~退化状态4.从每种状态的200组振动信号中各任选50组作为样本集,分别求取每组样本的RNE 和RQE作为退化特征。本文以正常样本为例介绍退化特征的提取过程。首先对50组正常样本和标准信号共51组样本进行S变换,得到51组S变换时频矩阵。然后根据S变换相对谱熵的定义和计算步骤计算50正常样本与标准信号的RNE和RQE.从两种故障模式各种故障程度的样本中各任选50组样本,采用同样的方式计算它们与标准信号的RNE和RQE.基于以上计算结果,从每种状态各任选10组进行分析,以验证所提出的退化特征表征液压泵退化状态的性能,它们的波形如图9、图10所示。
分析图9、图10可知,不论是滑靴磨损故障还是松靴故障,所提出两个特征指标都随着液压泵故障程度的加深呈现上升的趋势,且能够较好地区分液压泵的故障程度。本文采用两个退化特征组成液压泵的退化特征向量,则每种退化状态可得到50× 2退化特征集。
3.4退化状态识别
对于滑靴磨损故障,从5种退化状态的退化特征集中各任选10组退化特征向量,求每种状态下10组退化特征向量的平均值,基于该平均值建立液压泵滑靴磨损故障模式下退化状态识别的标准故障模式矩阵,结果如(16)式所示。

将各退化状态的剩余特征向量组成该状态的测试特征集,并做各退化特征集与标准故障模式矩阵灰关联分析,实现液压泵的退化状态识别。此处,以滑靴磨损故障模式下正常状态的识别为例,介绍液压泵的退化状态识别过程:分别计算各组样本特征向量与标准故障模式矩阵的灰色关联度,设定ρ为分辨率系数,本文研究取ρ=0.5,各样本与标准故障模式矩阵的灰色关联度和退化状态识别结果见表1.另外,分别对滑靴磨损故障模式下的其他4种退化状态进行状态识别,结果分别见表2~表5.
分析表1~表5可知,采用本文提出的方法能够很好的对液压泵出现滑靴磨损故障时的退化状态进行识别,正确识别率高达98%.采用同样的方法对液压泵出现松靴故障时的6种退化状态进行识别,也获得了很高的状态识别率。以上结果表明基于S变换相对谱熵和加权灰关联分析的退化识别方法能够很好地实现液压泵的退化状态识别。

图7 采集的部分振动信号Fig.7 Waveforms of collected vibration signals
4 结论
为更好地实现液压泵的退化状态识别,本文提出了基于RNE和RQE的液压泵退化特征提取方法。通过对仿真信号和液压泵实测信号分析得出:
1)特定故障模式下的RNE和RQE都随着故障程度的加深而上升,反映了各退化状态下振动信号能量概率分布和奇异值概率分布偏离正常状态振动信号概率分布的程度。
2)RNE和RQE能够很好地表征液压泵的退化状态,并能有效区分特定故障模式下的不同退化状态。

图8 平滑处理后的标准信号Fig.8 Standard vibration signal after smoothing
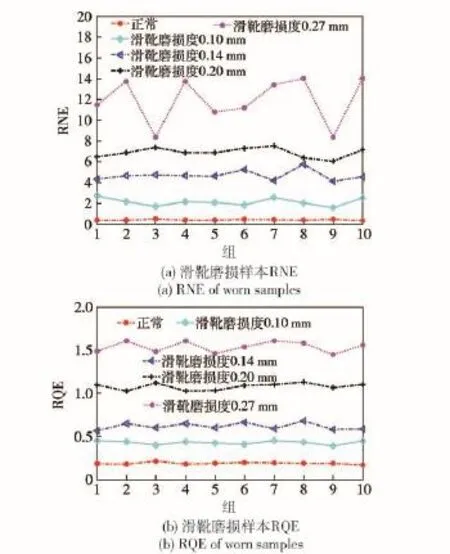
图9 滑靴磨损样本的退化特征Fig.9 Degradation features of worn samples
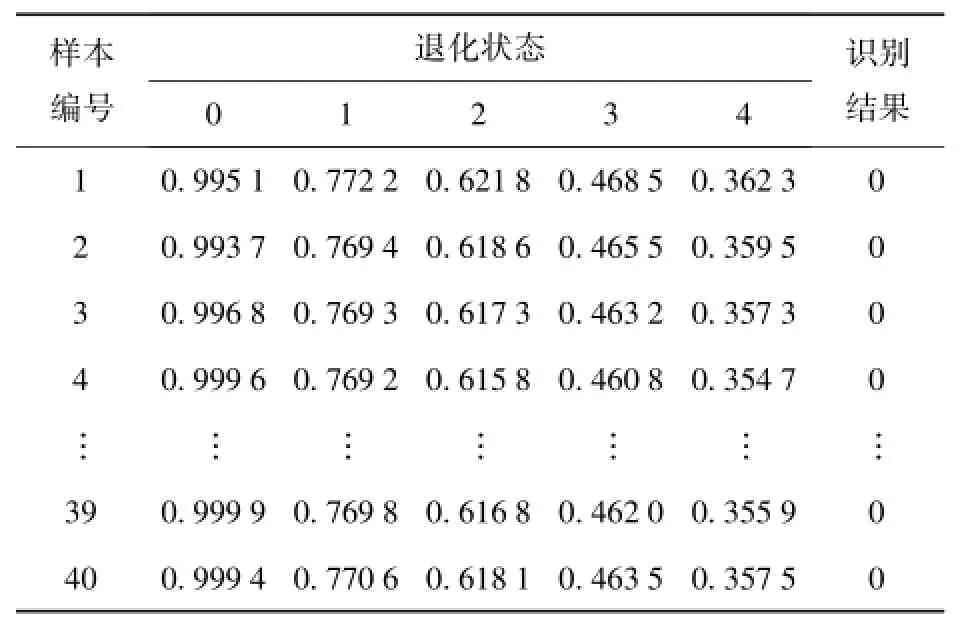
表1 滑靴磨损故障正常样本识别结果Tab.1 Identification results of normal samples during piston shoe wearing

图10 松靴样本的退化特征Fig.10 Degradation features of loosed slipper samples
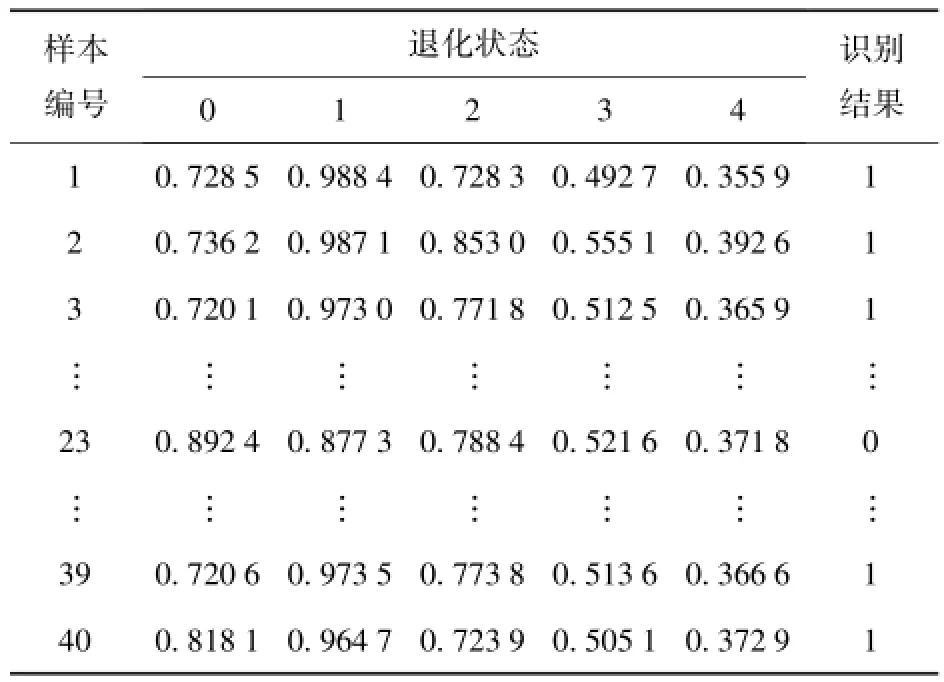
表2 滑靴磨损度为0.10 mm样本识别结果Tab.2 Identification results of 0.10 mm-worn samples during piston shoe wearing
3)通过对液压泵出现滑靴磨损故障和松靴故障时的样本进行分析,验证了所提出的基于S变换相对谱熵和加权灰关联分析的液压泵退化状态识别方法的有效性和可行性。

表3 滑靴磨损度为0.14 mm样本识别结果Tab.3 Identification results of 0.14 mm-worn samples during piston shoe wearing
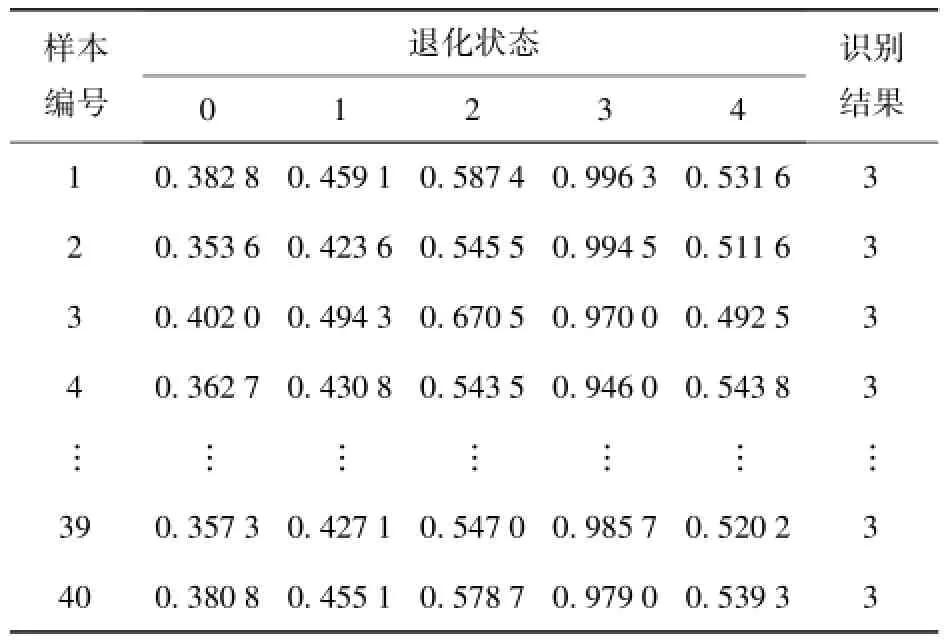
表4 滑靴磨损度为0.20 mm样本识别结果Tab.4 Identification results of 0.20 mm-worn samples during piston shoe wearing
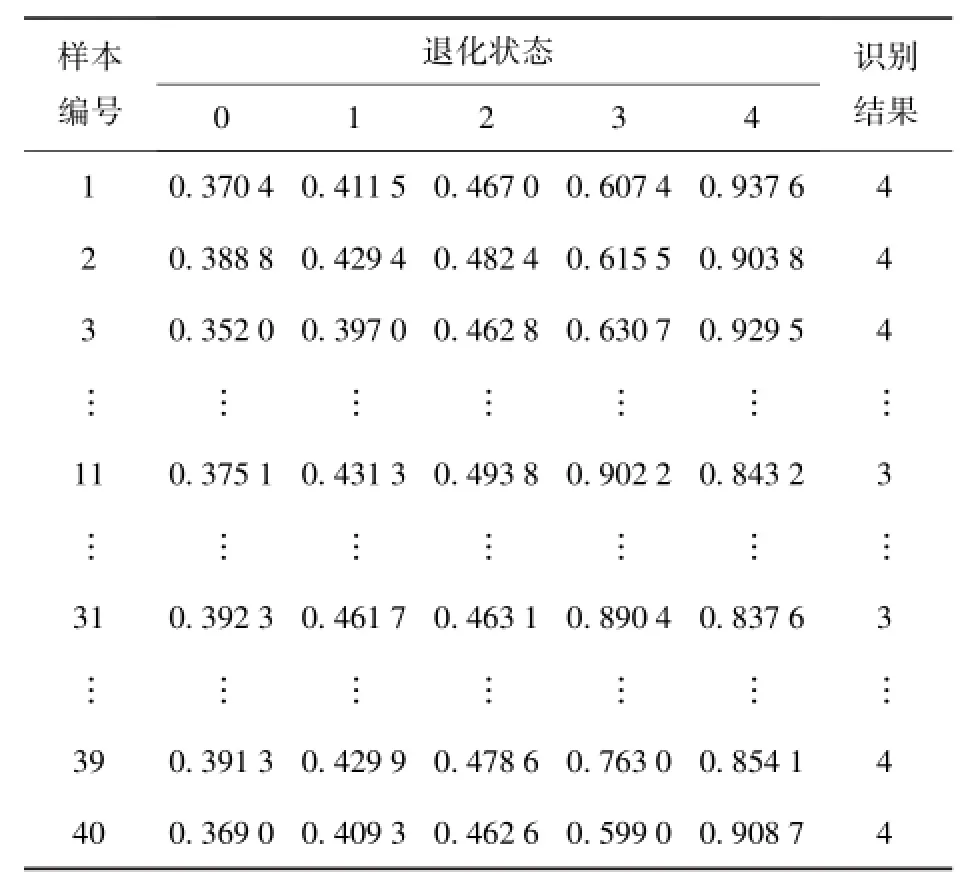
表5 滑靴磨损度为0.27 mm样本识别结果Tab.5 Identification results of 0.27 mm-worn samples during piston shoe wearing
参考文献(References)
[1] 李洪儒,许葆华.某型导弹发射装置液压泵故障预测研究[J].兵工学报,2009,30(7):900-906. LI Hong-ru,XU Bao-hua.Fault prognosis of hydraulic pump in the missile launcher[J].Acta Armamentrii,2009,30(7):900-906.(in Chinese)
[2] 张龙,黄文艺,熊国良.基于多尺度熵的滚动轴承故障程度评估[J].振动与冲击,2014,33(9):185-189. ZHANG Long,HUANG Wen-yi,XIONG Guo-liang.Assessment of rolling element bearing fault severity using multi-scale entropy [J].Journal of Vibration and Shock,2014,33(9):185-189. (in Chinese)
[3] Du J,Wang S P,Zhang H Y.Layered clustering multi-fault diagnosis for hydraulic piston pump[J].Mechanical Systems and Signal Processing,2013,36(2):487-504.
[4] 鞠华,沈长青,黄伟国,等.基于支持向量回归的轴承故障定量诊断应用[J].振动、测试与诊断,2014,34(4):767-771. JU Hua,SHEN Chang-qing,HUANG Wei-guo,et al.Quantitative diagnosis of bearing fault based on support vector regression [J].Journal of Vibration,Measurement&Diagnosis,2014,34(4):767-771.(in Chinese)
[5] Costa M,Goldberger A L,Peng C K.Multi-scale entropy analysis of biological signals[J].Physical Review E,2005,71(2):1-18.
[6] Wu S D,Wu C W,Lee K Y,et al.Modified multiscale entropy for short-term time series analysis[J].Physica A,2013,392(23):5865-5873.
[7] 张建宇,张随征,管磊,等.基于多小波包样本熵的轴承损伤程度识别方法[J].振动、测试与诊断,2015,35(1):128-132. ZHANG Jian-yu,ZHANG Sui-zheng,GUAN Lei,et al.Pattern recognition of bearing defect severity based on multi-wavelet packet sample entropy method[J].Journal of Vibration,Measurement& Diagnosis,2015,35(1):128-132.(in Chinese)
[8] 胡为,胡静涛.改进的符号时间序列分析方法及其在电机故障诊断中的应用[J].仪器仪表学报,2009,30(4):760-766. HU Wei,HU Jing-tao.Improved symbolic time series analysis method and its application in motor fault diagnosis[J].Chinese Journal of Scientific Instrument,2009,30(4):760-766.(in Chinese)
[9] 郭远晶,魏燕定,周晓军,等.S变换时频谱SVD降噪的冲击特征提取方法[J].振动工程学报,2014,27(4):621-628. GUO Yuan-jing,WEI Yan-ding,ZHOU Xiao-jun,et al.Impact extracting method based on S transform time-frequency spectrum de-noised by SVD[J].Journal of Vibration Engineering,2014,27(4):621-628.(in Chinese)
[10] 李战明,韩阳,韦哲,等.基于S变换的心音信号特征提取[J].振动与冲击,2012,31(21):179-183. LI Zhan-ming,HAN Yang,WEI Zhe,et al.Heart sound feature extraction based on S transformation[J].Journal of Vibration and Shock,2012,31(21):179-183.(in Chinese)
[11] 尹柏强,何怡刚,吴先明.心磁信号广义S变换域奇异值分解滤波方法[J].物理学报,2013,62(14):148702-1-148702-8. YIN Bai-qiang,HE Yi-gang,WU Xian-ming.A method for magnetocardiograms filtering based singular value decomposition and S-transform[J].Acta PhysicaSinca,2013,62(14):148702-1-148702-8.(in Chinese)
[12] Stockwell R G,Mansinha L,Lowe R P.Localization of the complex spectrum:the S transform[J].IEEE Transactions on Signal Pprocessing,1996,44(4):998-1001.
[13] Wang Y K,Li H R,Ye P.Fault feature extraction of hydraulic pump based on CNC de-noising and HHT[J].Journal of Failure Analysis and Prevention,2015,15(1):139-151.
[14] 王冰,李洪儒,许葆华.基于多尺度形态分解谱熵的电机轴承预测特征提取及退化状态评估[J].振动与冲击,2013,32(22):124-128. WANG Bing,LI Hong-ru,XU Bao-hua.Motor bearing forecast extracting and degradation status identification based on multiscale morphological decomposition spectral entropy[J].Journal of Vibration and Shock,2013,32(22):124-128.(in Chinese)
[15] 黎奇志,胡国平,赵红言.加权灰关联分析在故障诊断中的应用研究[J].微计算机信息,2012,28(7):28-30. LI Qi-zhi,HU Guo-ping,ZHAO Hong-yan.Research on the application of weighted grey relational analysis in fault diagnosis [J].Microcomputer Information,2012,28(7):28-30.(in Chinese)
[16] 申中杰,陈雪峰,何正嘉,等.基于相对特征和多变量支持向量机的滚动轴承剩余寿命预测[J].机械工程学报,2013,49(2):183-189. SHEN Zhong-jie,CHEN Xue-feng,HE Zheng-jia,et al.Remaining life predictions of rolling bearing based on relative features and multivariable support vector machine[J].Journal of Mechanical Engineering,2013,49(2):183-189.(in Chinese)
中图分类号:TH322;TP306+.3
文献标志码:A
文章编号:1000-1093(2016)06-0979-09
DOI:10.3969/j.issn.1000-1093.2016.06.003
收稿日期:2015-07-07
基金项目:国家自然科学基金项目(51275524)
作者简介:王余奎(1987—),男,讲师,博士。E-mail:wyktougao@163.com
S Transform Relative Spectrum Entropy and Its Application in Degradation State Identification of Hydraulic Pump
WANG Yu-kui1,2,LI Hong-ru1,HUANG Zhi-jie1,ZHAO Xu-cheng1
(1.Air Force Logistics College,Xuzhou 221000,Jiangsu,China;2.Ordnance Engineering College,Shijiazhuang 050003,Hebei,China)
Abstract:In order to characterize the degradation state of hydraulic pump,the degradation feature extraction method and degradation state identification method are studied.The degradation feature extraction method for pump which is named S transform relative spectrum entropy(STRSE)is proposed based on S transform(ST)for analyzing non-stationary vibration signal and relative entropy(RE)for characterizing the probability distribution difference among different signals.The analysis results of simulation signal demonstrate the availability and rationality of the proposed ST relative energy spectrum entropy(STRESE)and ST relative singular spectrum entropy(STRSSE)used as degradation features.The degradation feature vector is composed of the two features.The practical vibration signals of pump with piston shoe wear-out and loose faults are analyzed,and the results demonstrate the effectiveness of the proposed two features.The weighted grey relation method is used in the pump degradation state identification.A standard degradation mode matrix is built,and the degradation feature vectors of the samples to be identified are extracted.The grey relational analysis of degradation feature vectors and standard degradation mode matrix are performed.The grey correlation degrees are used to judge the degradation state of pump,and the analysis results demonstrate the favorable performance of the proposed method.
Key words:ordnance science and technology;hydraulic pump;degradation state identification;S transform;relative spectrum entropy;weighted grey relational analysis

