运用“弦长公式”优化解题策略

◇　河北　李文惠



通法研究

运用“弦长公式”优化解题策略

◇河北李文惠

圆锥曲线是高考数学必考内容之一,它一直扮演着让学生“谈虎色变”的角色,尤其是解答题的第2问或第3问,许多同学对此倍感困难乃至无从下笔．由于椭圆、双曲线、抛物线3者之间有许多共同的性质,而这些共性也常常成为考题命制的背景和源泉，因此,在平时的解题训练中,同学们一定要有意识地培养自己解题反思的习惯、发展变式拓展的思维,逐渐提高解决问题的能力和良好的数学素养．

在解圆锥曲线综合问题时,同学们常遇到这种情况:感觉方法是对的,但最后为什么算不下去?究其原因:解题思维没有做到合理的优化.

(1) 求椭圆方程;

(2) 斜率为k的直线l过点F,且与椭圆交于A、B2点,P为直线x=3上的一点,若△ABP为等边三角形,求直线l的方程.

几何问题代数化是处理解析几何问题的常用策略,解题中既可以将几何问题直接代数化,也可先把几何问题利用几何方法进行适度简化,再代数化.通常前者思维量小，但计算量大;后者计算量小，但思维量大．

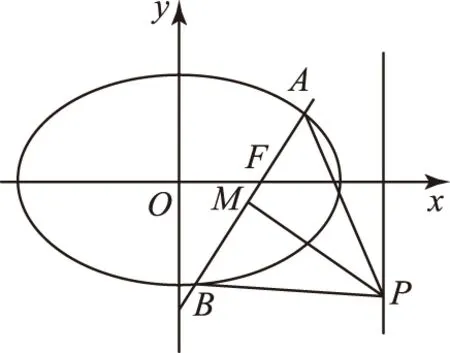
图1

代数化的主要途径是:设出直线与椭圆的2个交点坐标,将直线方程与椭圆方程联立,代入消元得含x或y的一元二次方程,由直线与椭圆有2个交点,则一元二次方程有2个实根,即判别式大于0,再结合根与系数的关系得2交点的横坐标(纵坐标)之和、积与直线斜率之间的关系．再根据题意结合平面几何图形的相关性质,列出关系式求解即可.

对于第(2)问部分同学的解题思路是:

设AB的中点为M(x0,y0)，可得

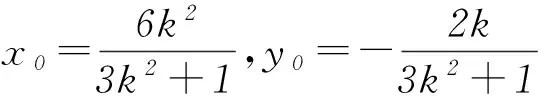
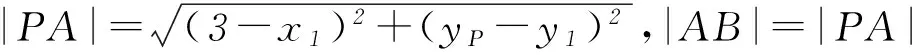
也有同学想到利用等边三角形的性质

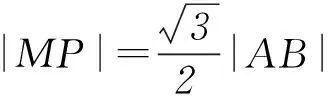
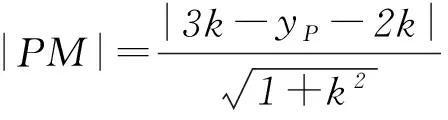
当然从解题思维来看第2种思路明显要优于第1种思路,但为何仍无法求解呢?在第2种思维的基础上能否将其进一步优化?

思维受阻的原因是受到弦长公式中“弦长”二字的局限．提到弦长公式,我们主观上一直认为是直线被曲线所截的两点A、B间的距离,其实则不然,对于一条直线上任意不重合的2个点之间的距离,都可以利用此公式求．

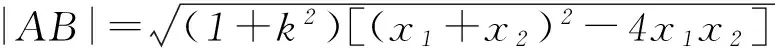
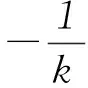
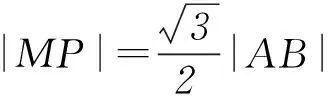
圆锥曲线的运算问题不仅涉及圆锥曲线的定义、方程、几何性质,还可以与函数、方程、不等式、三角、平面向量等知识交会,综合性强,能力要求高,成为历年高考格外关注的热点．这就要求我们在处理问题时既要“大处着眼”,即在整体上把握问题的综合信息和处理问题的数学思想,又要“小处着手”,即在细节上能熟练运用各种数学方法与技巧．因此掌握一些简化圆锥曲线运算的策略,对优化解题过程、提高运算效率大有裨益．

通过上述分析,笔者建议同学们在解答圆锥曲线问题时可从以下几方面来着手: 1)熟悉常见模型; 2)熟练掌握圆锥曲线问题中常见的基本方法和基本技巧; 3)认真审题,理清题中的基本关系和内在结构; 4)善于发现利用; 5)加强代数运算、变形能力; 6)尽量使用原始数据; 7)增强自信心.

在解题时若能适当地运用上述策略，对优化解题过程、简化圆锥曲线运算起着很大的作用，从而使解题过程更加优美、简洁.

(作者单位：河北省滦平县第一中学)