格点大气环流模式GAMIL2参数不确定性的量化分析与优化

张涛, 谢丰, 薛巍*, 李立娟, 许皓宇, 王斌2,

1 清华大学计算机科学与技术系， 北京　100084 2 清华大学地球系统科学研究中心， 地球系统数值模拟教育部重点实验室， 北京　100084 3 中国科学院大气物理研究所大气科学与地球流体力学数值模拟国家重点实验室, 北京　100029



格点大气环流模式GAMIL2参数不确定性的量化分析与优化

张涛1,2, 谢丰3, 薛巍1,2*, 李立娟3, 许皓宇1, 王斌2,3

1 清华大学计算机科学与技术系， 北京100084 2 清华大学地球系统科学研究中心， 地球系统数值模拟教育部重点实验室， 北京100084 3 中国科学院大气物理研究所大气科学与地球流体力学数值模拟国家重点实验室, 北京100029

摘要物理过程参数化方案的不确定性是目前气候系统模式不确定性的重要来源之一.随着模式内在复杂度攀升，模拟场景多样化，参数化方案中基于先验的和人工的物理参数选取方法已经逐步成为限制模式模拟能力的瓶颈之一.为此，本文设计并提出了初选与寻优相结合的两步法参数优化方案.初选阶段用全因子采样方法对不确定参数空间进行初始敏感性分析，估计最优解所在区域；寻优步采用单纯型下山法，基于初选阶段确定的参数组合快速寻优.将两步法应用于中国科学院大气物理研究所(英文缩写：IAP)大气科学和地球流体力学数值模拟国家重点实验室(英文缩写：LASG)格点大气模式第2版：GAMIL2，选取其深对流方案和云量方案中的3个重要参数开展寻优，优化以综合减小模式降水、风场、温度、湿度、位势高度以及辐射通量的误差为目标.这些变量用GAMIL2标准版本标准化后形成单一的目标. 结果显示，优化后的目标函数值比GAMIL2 标准版本改进了7.5%.机理分析表明，调优后的参数优化了大气中的水汽凝结作用，进而减少模式的湿度偏差，改进云量的模拟效果；同时水汽凝结作用的变化通过大气内部动力和热力相互作用及响应影响温度、位势高度和风场的模拟.

关键词气候系统模式； 物理参数化方案； 不确定性量化分析； 优化算法； 机理分析

1引言

气候系统模式是研究气候演变规律、预估/预测未来气候变化趋势不可或缺的工具.参加政府间气候变化专门委员会(IPCC)第4次评估报告(AR4)的21个气候系统模式在未来大气温室气体中等排放情景(A1B)下对未来100年预估的全球平均温度和降水变化与多模式间的差别相接近1)1) http:∥www.ecmwf.int/newsevents/meetings/workshops/2011/Model_uncertainty/presentations/Murphy.pdf(IPCC, 2007)，即多模式预估未来升温2.8°C，而模式跟模式之间的差别就达到了2.5°C.参加IPCC第5次评估报告(AR5)的模式，虽然比AR4的模式分辨率有所提升，物理参数化方案有所改善，但温度以及降水的变化却极其相似，不确定性并没有显著减小(Knutti and Sedlacek，2013).如此大的模式不确定性将严重影响模式的可信度.另一方面，模式模拟结果的不确定性主要源自模式初值、外强迫、数值离散、模式物理过程的参数化过程和参数变化等(Stainforth et al.，2007；Knutti，2008).其中，参数的不确定性可以通过定量化方法分析： Li等(2013)采用局部和全局敏感性分析方法对CoLM模式的40个不确定性参数进行敏感性分析，筛选出敏感性较高的参数；Sun等(2013)利用多链马尔科夫链蒙特卡洛(Markov Chain Monte Carlo，MCMC)获得CLM4模式不确定性参数的后验分布，缩减不确定参数范围.Yang等(2013)研究了CAM5的不确定性参数，采用随机近似模拟退火方法对模式的对流降水进行调优.Zou等(2014)采用了多链模拟退火方法，在东亚季风模拟的优化中效果明显.Severijns and Hazeleger(2005)采用了单纯型下山法对Speedy大气模式与能量平衡有关的不确定性参数进行调优.这些工作都不同程度地改进了模式的模拟性能.上述研究都是针对模式不确定参数量化分析的某一个方面进行，然而目前针对参数自动寻优框架和气候系统模式整体性能调优的研究并不多.

气候系统模式物理过程性能的提升得益于物理参数化方案的改善以及不确定性参数的调优.传统的参数调优大都是手工方法，基于对模式结果的诊断分析，人为选择参数值.该方法极大地利用了专家知识，但对于复杂的强非线性模式而言，很难得到客观和精细的优化结果.参数自动寻优机制将最优化算法和不确定性分析相结合，形成以参数初值选择、模式运行、目标函数设计以及参数寻优为主的工作流，最终得到参数空间中的优化参数组合.自动参数寻优面临的挑战主要有两个方面：一方面，针对气候系统模式的自动调优平台更加复杂，气候系统是强非线性的混沌系统，spin-up过程需要的时间长，不确定性参数多，参数间存在复杂的相互作用，需要进行参数敏感性分析以及设计更快速有效的优化算法；另一方面，针对模式整体性能的调优，制定全面表征模式性能的目标函数并使其得到优化是困难的，敏感参数的优化能够改进模式某些方面的模拟性能，但很难保证模式整体性能的改进.

单纯型下山法是一种利用多面体来代表调优参数空间，通过不断改变其几何形状达到收敛的最优化方法，对参数维数和精度要求不高的问题收敛速度较快，相对集合卡尔曼滤波和遗传算法等基于每个迭代步多个样本的算法，计算成本大大减小.但由于其局部寻优的特点，调优结果严重依赖于初始条件.

本文综合不确定参数的敏感性分析和最优化算法，提出参数初选与寻优相结合的两步法参数优化方案.初选阶段用全因子采样方案对不确定参数空间进行等密度采样，对敏感区域做加密采样，评估最优解所在区域；寻优步采用单纯型下山法，利用初选阶段选取的，目标函数值较好的参数组合为初值进行快速寻优.本文将它们用于中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室格点大气模式第2版(GAMIL2)，改进模式多年年平均的模拟性能.

2模式介绍和目标函数

2.1GAMIL2模式

本文所用的模式是中国科学院大气物理研究所LASG发展的格点大气环流模式第2版(GAMIL2).该模式参加了IPCC AR5的大气模式比较计划(Atmospheric Model Inter-comparison Project,AMIP)和云反馈模式比较计划(Cloud Feedback Model Inter-comparison Project,CFMIP)，并作为FGOALS-g2(Flexible Global-Ocean-Atmosphere-Land System Model grid version 2)的大气分量完成了耦合模式比较计划(CMIP5).其当前标准版本采用水平分辨率为2.8°×2.8°，垂直方向分为26层.模式的动力框架采用了有限差分方案，严格保持了总质量守恒和标准层结扣除后总有效能量守恒(Wang et al.，2004).水汽平流方案采用两步保形正定方案(Yu，1994).GAMIL2在GAMIL1的基础上更新了云相关过程(Li et al.，2013)，深对流参数化方案采用Zhang and Mu方案(2005)， 对流云量采用Xu and Krueger方案(1991), 云微物理过程采用Morrison and Gettleman方案(2008).其中对深对流、浅对流、云量、云微物理过程以及边界层等方案的14个不确定性参数已经完成了手动调优.作为自动调优的第一步，本文在手动调优基础上选择3个(两个来自深对流方案，一个来自云量方案)较高敏感性的重要参数，分别是深对流的云水雨水自动转换率c0，对流降水蒸发率ke，低云生成的相对湿度阈值rhminl.具体的参数物理学含义参照附录说明.3个参数的取值范围略大于或者等于其他类似参数(Yang et al.，2013；Jackson et al.，2008)所选范围，如表1所示(Li et al.，2013).参数的初值为GAMIL2参加IPCC AR5 试验的配置，利用这组参数得到的模拟结果我们称之为CNTL试验结果.模式自2000年启动，模拟5年，取后3年输出的平均做诊断分析.

表1　深对流和积云参数化方案选择的不确定参数

2.2观测资料

风场、温度、湿度和位势高度都采用欧洲中期天气预报中心(European Center for Medium-Range Weather Forecasts, ECMWF)的再分析资料ERA-Interim (Simmons et al., 2007)，时间段为1989—2004年，水平分辨率均为1.5°×1.5°.降水资料来源于全球降水气候态研究计划(Global Precipitation Climatology Project, GPCP；Adler et al., 2003)，时间段为1989—2004年，水平分辨率为2.5°×2.5°.辐射采用地球辐射收支试验(Earth Radiation Budget Experiment, ERBE)的卫星资料(Barkstrom, 1984)，时间段为1985—1989年，水平分辨率为1.875°×1.875°.针对后期的机理探讨，我们还用到国际卫星云气候计划(International Satellite Cloud Climatology Project, ISCCP；Rossow and Schiffer， 1999)的云量资料，时间段为1989—2004年，水平分辨率为2.5°×2.5°.所有资料先计算其气候平均态，再插值到GAMIL2的水平网格上.

再分析资料(1989—2004年)和模拟(2000—2004年)时间存在一定程度的不一致，其原因在于优化过程是多步迭代过程，若积分时间太长，计算量将非常惊人，为此选取了再分析资料后5年2000—2004年这个时间窗口，采用模式模拟5年，分析其后3年的结果.同时，为了确保参数调优结果的有效性，将本文得到的优化参数用于模式进行长时间(1989—2004年)积分时，目标函数的变化与本文一致.

2.3目标函数

从整体上去改进模式模拟性能是模式发展的关键，因此，本文选择风场、温度、湿度、位势高度、降水和辐射通量等变量进行较为全面的诊断(Murphy et al.，2004；Gleckler et al.，2008；Reichler and Kim，2008).目标函数计算过程如下：首先，分别计算上述各个变量的模拟值和观测的空间分布均方误差(公式(1))作为目标函数的统计手段(Taylor, 2001)；其次，为将不同变量均方误差有效整合，采用GAMIL2参数IPCC AR5的试验结果相对观测的均方误差(公式(2))作为分母标准化各变量均方误差，无量纲化后的各变量因子累加结果除以变量总数作为目标函数2(公式(3)).具体的诊断变量和公式(2)的参考均方根误差详见表2.因此，如果新的模拟使得2<1，则结果得到了优化.调优试验(EXP)的目的就是寻找一组参数，使其对应的目标函数值最小.

(1)

(2)

(3)

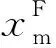
3方法

本文设计并实现了参数自动调优框架，如图1所示.首先，利用Problem Solving environment for Uncertainty Analysis and Design Exploration(PSUADE)(Tong，2005)工具对不确定的参数空间进行初始化采样，评估最优解所在范围，为优化算法提供高效的寻优初值.PSUADE是Lawrence Livermore National Laboratory(LLNL)发展的不确定性量化分析软件包，支持多种采样方法.第二阶段采用单纯型下山法在最优解区域内进行局部寻优.自动寻优框架包括两部分，模式组件和调优组件.其中模式可以是分量模式、耦合模式或代理模式；调优组件可以支持单纯型下山法、遗传算法、差分进化和粒子群等多种调优算法，并借助PSUADE完成初始采样.这两个组件是松耦合的，可以灵活选择和配置不同的优化算法和模式.

3.1粗调——敏感性分析

气候模式的参数优化是一个全局优化问题.为了有效利用单纯型算法的快速收敛和计算成本低的优势，并克服其局部收敛的不足，需要对参数空间进行初始敏感性分析，并为单纯型算法设置起调初值.全因子采样方法是一种在取值范围内的等距离采样，在参数维度不高的情况下，适合全面分析参数值对目标函数的敏感性.本文对所选的3个参数在给定的取值范围内分别进行全因子采样，在敏感性较高的区间进一步加密采样，根据每组参数组合的模式输出，计算目标函数，如表3所示.选择的初值遵循两个原则，目标函数值小以及调优的参数自由度大，也就是有效确定最优解所在区域，并尽可能让更多的参数参于扰动调优.表3中第2、5、15、19为选择的满足上述条件的参数自动寻优初值.

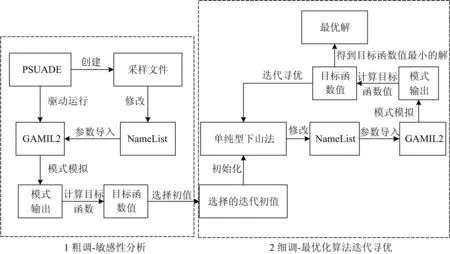
图1　自动参数调优框架Fig.1　The automatic framework of calibrating parameters

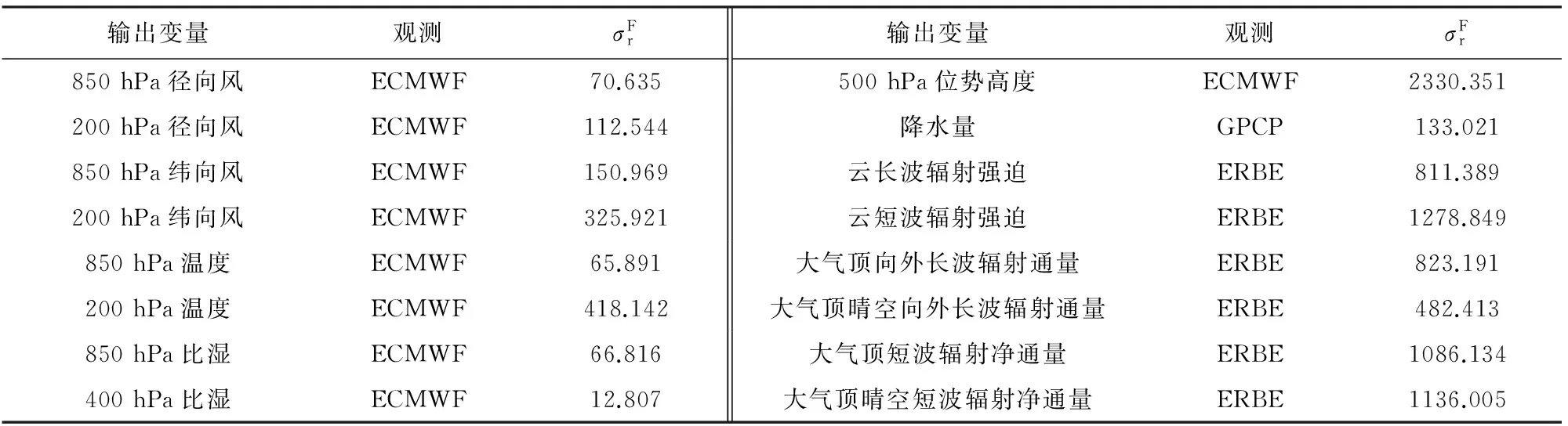
表2　目标函数包括的模式输出变量

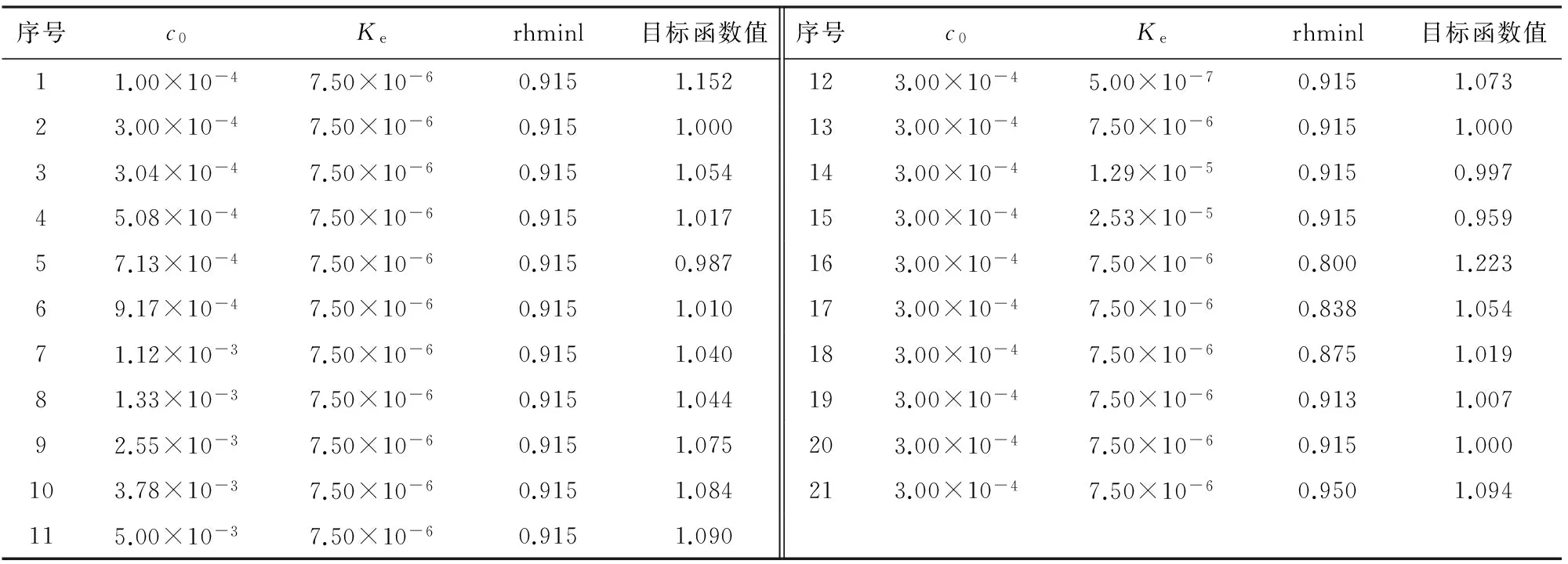
表3　参数全因子采样的参数组合及对应的目标函数值

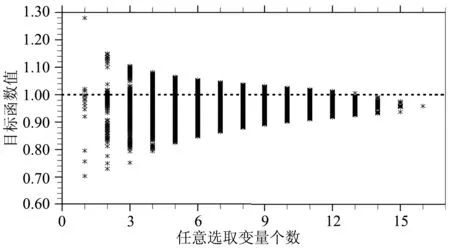
图2　不同变量组合数下目标函数值散点图Fig.2　The metrics scatter diagram of different variables combinations

3.2细调——参数自动寻优

单纯型下山算法是一种著名的非线性优化算法，特别适合于导数不可知或者难于获得的非线性优化问题.该算法利用简单的几何图形，通过不断改变几何形状，用目标函数值较小的顶点取代目标函数值最大的顶点，在给定的终止条件下，经过反复迭代逐步确定最优点.该方法在参数维度不高的情况下，能够快速收敛.

本文中，单纯型算法迭代了100步，在第38步得到该范围内的最小目标函数值0.92569，对应的参数为c0=4.312706×10-4,ke=7.51878×10-6, rhminl=9.145474×10-1(称该样本为EXP试验组).调优后的目标函数比GAMIL2 的标准版本降低了7.5%.作为局部优化算法，初值的选取至关重要.测试显示，如果随机选择优化算法的初值，在200迭代步内得不到比敏感性分析阶段更优化的结果.

表4列举了EXP试验全球、热带地区(30°S—30°N)和两半球中高纬地区的模式输出单变量和综合变量的目标函数值.总体来说热带地区调优效果最好，南半球热带外区域次之，北半球热带外区域相对较差，但三者的综合目标函数都相对CNTL有明显改善；高层的风场和湿度场的改进幅度大于低层；400 hPa湿度场、200 hPa纬向风和500 hPa位势高度是改进最明显的三个变量，云长波辐射强迫、200 hPa温度和大气顶向外长波辐射强迫是比CNTL变差幅度最大的三个变量，这些变量改进/变差的最大贡献均来自热带地区.

表4　EXP试验组不同地区单变量及综合变量的目标函数值

4结果分析和机理探讨

与CNTL试验相比，EXP试验增大了深对流中的云水雨水转化率(c0)和对流降水蒸发率(ke).c0增大使得大气中的更多云水转化成雨滴.一部分雨滴在其下落过程中会蒸发为水汽，ke的增大进一步增强了蒸发作用，总体上削弱了深对流的凝结过程，从而加湿600 hPa高度以下的大气.由于对流和层云过程的相互作用，对流凝结过程的减弱也会导致层云凝结过程减弱(Mapes， 2000；Houze，1997)，具体表现为高层凝结减弱，中低层蒸发减弱，降低了400 hPa高度的大气湿度.深对流凝结和层云凝结过程的强度变化共同作用于模式湿度模拟的改进.CNTL试验中，低层水汽模拟偏低，在低纬度850 hPa高度附近存在明显的负偏差中心，而副热带700 hPa至500 hPa间的水汽模拟偏高，图中可以看到3个偏差较大的区域(图3).EXP试验中，湿物理过程加湿率的改变使得这些偏差都有所削减，同时减弱了CNTL试验中高层的湿偏差和低层的干偏差(图3)，高层和低层水汽的均方根误差也均减小(表4)，明显改进了模式对于湿度模拟的效果.GAMIL2的云量(由稳定度诊断的海洋性层云除外)模拟由湿度诊断得到，总的来说，湿度越高，云量越多.尽管云量并没有直接包括在目标函数中，大气湿度模拟的改进进一步优化了模式对于云量的模拟.EXP试验中，不同高度云量(包括高云、中云以及低云)模拟结果的均方根误差相比于CNTL试验均减小，同时由于大气中高层湿度降低，高云和中云的整体均值也有所下降，与ISCCP资料的结果更为接近(表5，图3，图4).

表5　高云、中云和低云气候平均态

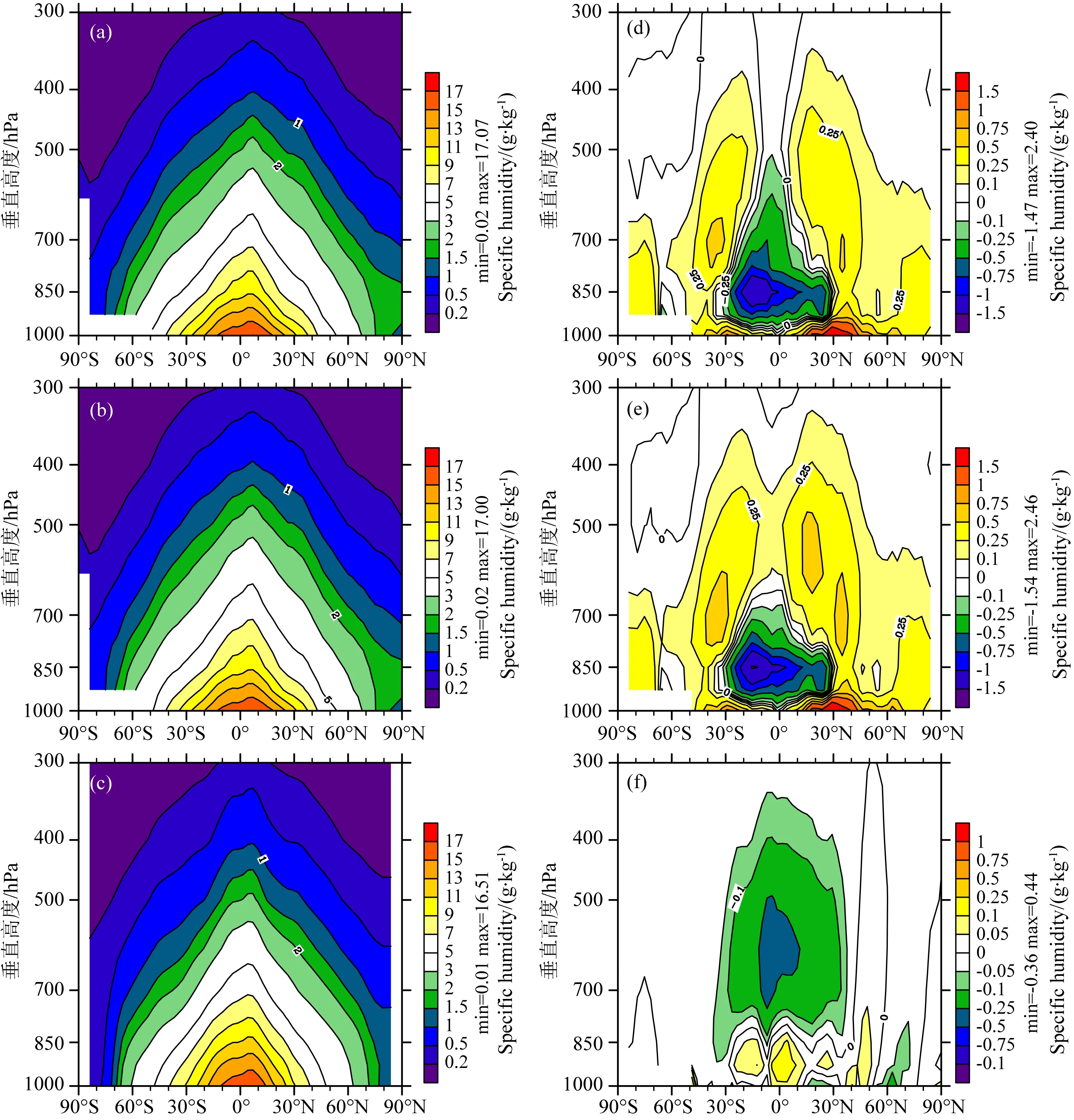
图3　EXP(a)，CNTL(b)与再分析资料ECWMF(c)的湿度纬向平均-高度分布，EXP和CNTL分别与再分析资料之差(d，e)以及二者之差(f)Fig.3　Pressure-latitude distributions of specific humidity of EXP (a), CNTL (b), observations (c), EXP-observations (d), CNTL-observations (e), and EXP-CNTL (f)

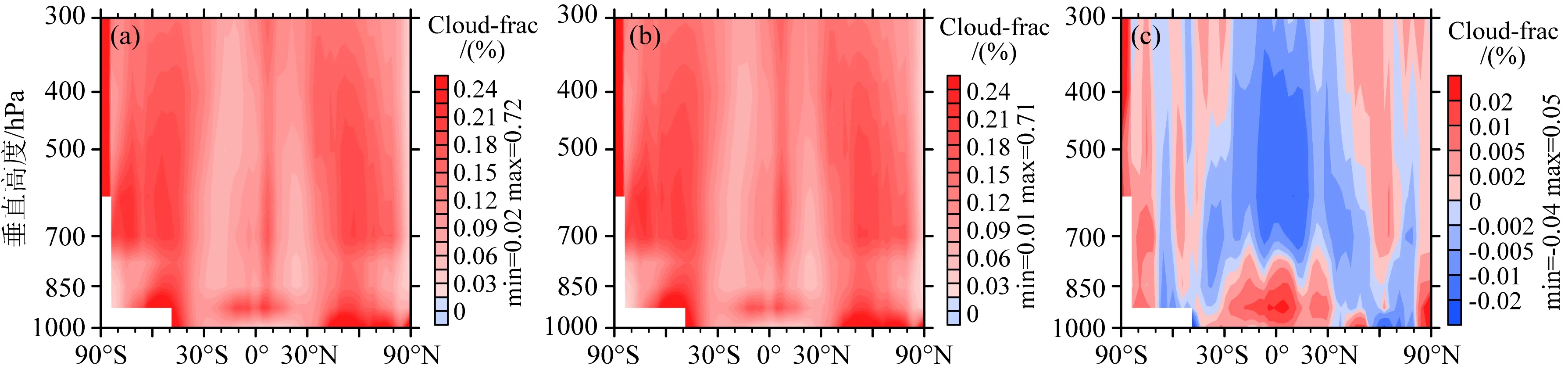
图4　EXP(a)，CNTL(b)的云量纬向平均-高度分布，以及二者之差(c)Fig.4　Pressure-latitude distributions of cloud fraction of EXP (a), CNTL (b), EXP-CNTL (c)

模式湿物理过程的凝结作用直接影响模式对非绝热加热场的模拟.凝结加热增强(减弱)在低纬热带地区主要依靠绝热上升冷却作用的增强(减弱)来平衡，而在中高纬地区主要由水平冷平流的增强(减弱)来平衡(吴国雄等，2002)，并进一步通过动力和热力相互作用及响应(Yang et al.，2013；Zhang et al.，2013；Zhang etl al.，2011)影响温度、位势高度的模拟.EXP试验改进了对流层中层500 hPa位势高度的模拟，偏差的极值由CNTL试验的156.36(-65.86)m减小至EXP试验的141.83(-56.41)m，同时均方根误差也由32.46 m减小为28.65 m，500 hPa位势高度的全球平均值、最大值和最小值都与再分析资料更为接近(图5).从空间分布上看，优化效果最大的区域主要位于热带地区和南半球中高纬度地区.CNTL试验中，500 hPa位势高度的模拟效果与再分析资料相比，热带地区整体模拟结果偏高，同时在日界线以东30°S—60°S有较大的负偏差，而在60°S—90°S有较大的正偏差.调优后，这两个地区的偏差得到缓解.另外，位于30°N附近大西洋地区以及加拿大北部的正偏差也有一定程度的改进.

纬向风的分布反映了大气环流的基本状态，其模拟效果与位势高度密切相关，对于模式性能有着重要影响.200 hPa纬向风的最主要特征为赤道附近的东风带和南北半球副热带地区的西风带，优化前后的CNTL和EXP试验都能够再现这一特征(图6).CNTL试验在东半球严重高估了热带地区的东风和30°S—50°S之间的西风，低估了30°N和60°S附近的西风；在西半球的偏差与东半球大致相反：低估热带的东风、60°N附近和30°S附近的西风，高估40°N—50°N之间的西风.其中热带外60°N和30°S—50°S之间的西风偏差和30°N和60°S附近的东风偏差是目前参加IPCC AR4和AR5模式所共有的偏差，其原因还有待进一步探究(Lee et al., 2013).EXP试验的偏差分布虽与CNTL的一致，但在热带东风带、南印度洋等区域偏差强度有明显减小；偏差的极值和全球均方根误差也分别由CNTL的16.16(-11.66)和4.54 m·s-1减小至EXP的12.47(-10.25)和3.84 m·s-1.同时也需注意到EXP试验在南美南部洋面的东风偏差相比CNTL进一步加大，全球平均值偏差也增大了0.07 m·s-1.这也在一定程度上暗示了在全球模式中引入具有空间分布的物理参数(Zhang et al., 2011)以及在目标函数包含平均值偏差的必要性.

EXP试验通过优化深对流参数，显著改进了热带区域的中高层变量(表4).而对于热带外区域和热带低层，是通过深、浅对流等湿过程的相互作用和低云生成的湿度阈值的减小(外界环境不变的情况下，低云增加)共同作用影响.此外北半球中高纬度还受陆气相互作用的影响，因此其改进效果逊于南半球.

图5　EXP(a)，CNTL(b)与再分析资料ECWMF(c)的500 hPa位势高度，EXP和CNTL分别与再分析资料之差(d，e)以及二者之差(f)Fig.5　Annual mean geopotential height at 500 hPa of EXP (a), CNTL (b), observations (c), EXP-observations (d), CNTL-observations (e), EXP-CNTL (f)

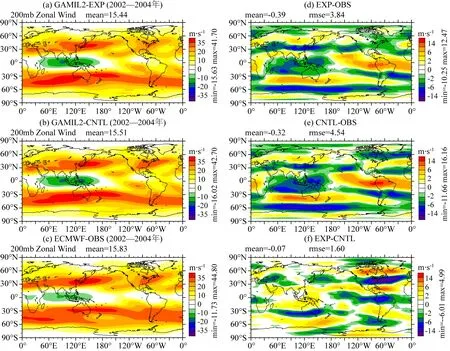
图6　EXP(a)，CNTL(b)与再分析资料ECWMF(c)的200 hPa纬向风，EXP和CNTL分别与再分析资料之差(d，e)以及二者之差(f)Fig.6　Annual mean meridional wind at 200 hPa of EXP (a), CNTL (b), observations (c),EXP-observations (d), CNTL-observations (e), EXP-CNTL (f)

5结论与讨论

本文构建了通用的参数调优框架，采用两步法对GAMIL2大气模式物理过程中的关键不确定参数进行了自动调优.首先，为了克服单纯型下山法初值依赖和局部收敛的不足，以及适应气候系统模式强非线性的特点，在不确定参数空间中进行全因子采样，初步分析最优解所在范围，为优化算法提供高效的寻优初值.然后采用单纯型下山法迭代寻优，收敛速度快，计算成本低.算法在第38步获得优化解，目标函数值比GAMIL2模式的标准参数配置优化了7.5%.降水、湿度和位势高度等变量的误差均得到明显改进.

对调优后参数模拟结果的机理分析表明深对流中的云水雨水转化率和降水增发率的增加，共同导致了深对流凝结和层云凝结过程减弱，直接影响温湿等廓线的分布；通过动力和热力相互作用间接影响温度、位势高度、风场等变量的分布.最终，标准试验中热带偏干和降水偏多等现象在优化试验中得到明显改善.

尽管本文提出并设计实现的参数调优算法取得了较为理想的调优效果，但仍面临诸多挑战.单纯型下山法存在并行化困难的问题，对于高维问题，其适应性也需要进一步研究.在调优过程中，目前目标函数基于均方误差建立，需要建立一个包括均方误差、均值、极值等，甚至包括变率的综合目标函数.同时，多源观测资料的协调性和物理参数影响模拟性能的详细物理机制也值得深入讨论.

附录

Zhang-McFarlane深对流方案是一种总体型质量通量方案.该方案认为当对流层低层出现局地不稳定时，会产生对流尺度的上升气流.伴随上升气流，水汽凝结成云水.根据经验公式(Lord et al., 1982)，云水进一步转换为雨水Rr：

Rr=C0Mul

(1A)

Mu表示对流云上升气流的质量通量，C0表示深对流云水雨水自动转换率，l表示云水含量.

一部分雨水在下落过程中发生蒸发，蒸发过程的计算采用Sundqvist(1988)公式：

Ek=ke(1-RHk)Rk

(2A)

其中，Rk表示模式第k层的降水通量，RHk表示环境的相对湿度，ke表示深对流降水的蒸发率.GAMIL2中的低云定义为750 hPa以下的云，低云云量由相对湿度诊断得到：

(3A)

RH表示大气的相对湿度，rhminl表示低云生成的相对湿度阈值.低云生成的条件是RH大于rhminl.

References

Adler R F, Huffman G J, Chang A, et al. 2003. The version-2 Global Precipitation Climatology Project (GPCP) monthly precipitation analysis (1979-present).J.Hydrometeor., 4(6): 1147-1167.Barkstrom B R. 1984. The earth radiation budget experiment (ERBE).Bull.Amer.Meteor.Soc., 65(11): 1170-1185.

Li J D, Duan Q Y, Gong W, et al. 2013. Assessing parameter importance of the Common Land Model based on qualitative and quantitative sensitivity analysis.Hydrol.EarthSyst.Sci.Discuss., 10(2): 2243-2286.

Li L J, Wang B, Dong L, et al. 2013. Evaluation of grid-point atmospheric model of IAP LASG version 2 (GAMIL2).Adv.Atmos.Sci., 30(3): 855-867.

Lord S J, Chao W C, Arakawa A. 1982. Interaction of a cumulus cloud ensemble with the large-scale environment. Part IV: The discrete model.J.Atmos.Sci., 39(1): 104-113.

Mapes B E. 2000. Convective inhibition, subgrid-scale triggering energy, and stratiform instability in a toy tropical wave model.J.Atmos.Sci., 57(10): 1515-1535. Morrison H, Gettelman A. 2008. A new two-moment bulk stratiform cloud microphysics scheme in the Community Atmosphere Model, version 3 (CAM3). Part I: Description and numerical tests.J.Climate, 21(15): 3642-3659. Murphy J M, Sexton D M H, Barnett D N, et al. 2004. Quantification of modelling uncertainties in a large ensemble of climate change simulations.Nature, 430(7001): 768-772.

Reichler T, Kim J. 2008. How well do coupled models simulate today′s climate?Bull.Amer.Meteor.Soc., 89(3): 303-311.

Rossow W B, Schiffer R A. 1999. Advances in understanding clouds from ISCCP.Bull.Amer.Meteor.Soc., 80(11): 2261-2287.

Severijns C A, Hazeleger W. 2005. Optimizing parameters in an atmospheric general circulation model.J.Climate, 18(17): 3527-3535.

Simmons A J, Uppala S M, Dee D P, et al. 2007. ERA-Interim: New ECMWF reanalysis products from 1989 onwards.ECMWFNewsletter, 110(110): 25-35. Stainforth D A, Allen M R, Tredger E R, et al. 2007. Confidence, uncertainty and decision-support relevance in climate predictions.Philos.Trans.Roy.Soc.A, 365(1857): 2145-2161. Sun Y, Hou Z, Huang M, et al. 2013. Inverse modeling of hydrologic parameters using surface flux and runoff observations in the Community Land Model. Hydrol.EarthSyst.Sci.Discuss., 10(4): 5077-5119.Sundqvist H. 1988. Parameterization of condensation and associated clouds in models for weather prediction and general circulation simulation//Physically-Based Modelling and Simulation of Climate and Climatic Change. Netherlands: Springer, 433-461.

Taylor K E. 2001. Summarizing multiple aspects of model performance in a single diagram.J.Geophys.Res.:Atmos., 106(D7): 7183-7192.

Tong C. 2005. PSUADE user’s manual. Lawrence Livermore National Laboratory (LLNL), Livermore, CA, 109.

Wang B, Wan H, Ji Z Z, et al. 2004. Design of a new dynamical core for global atmospheric models based on some efficient numerical methods.Sci.ChinaSer.A-Math.Sci., 47(Suppl.): 4-21.Wu G X, Chou J F, Liu Y M, et al. 2002. Dynamics of the Formation and Variation of Snbtropical Anticyclones (in Chinese). Beijing: Science Press.Xu K M, Krueger S K. 1991. Evaluation of cloudiness parameterizations using a cumulus ensemble model.Mon.Wea.Rev., 119(2): 342-367.

Yang B, Qian Y, Lin G, et al. 2013. Uncertainty quantification and parameter tuning in the CAM5 Zhang-McFarlane convection scheme and impact of improved convection on the global circulation and climate.J.Geophys.Res.:Atmos., 118(2): 395-415.

Yu R C. 1994. A two-step shape-preserving advection scheme.Adv.Atmos.Sci., 11(4): 479-490. Zhang C X, Wang Y Q, Hamilton K. 2011. Improved representation of boundary layer clouds over the southeast Pacific in ARW-WRF using a modified Tiedtke cumulus parameterization scheme.Mon.Wea.Rev., 139(11): 3489-3513. Zhang G J, Mu M Q. 2005. Effects of modifications to the Zhang-McFarlane convection parameterization on the simulation of the tropical precipitation in the National Center for Atmospheric Research Community Climate Model, version 3.J.Geophys. Res., 110(D9):D09109,doi: 10.1029/2004JD005617.

ZhangH,LinZH,ZengQC. 2011.Themutualresponsebetweendynamicalcoreandphysicalparameterizationsinatmospheric

general circulation models.ClimaticEnviron.Res., 16(1): 15-30.

Zhang H, Zhang M H, Zeng Q C. 2013. Sensitivity of simulated climate to two atmospheric models: Interpretation of differences between dry models and moist model.Mon.Wea.Rev., 141(5): 1558-1576.

Zou L W, Qian Y, Zhou T J, et al. 2014. Parameter tuning and calibration of RegCM3 with MIT-emanuel cumulus parameterization scheme over CORDEX East Asia domain.J.Climate, 27(20): 7687-7701.

附中文参考文献

吴国雄, 丑纪范, 刘屹岷等. 2002. 副热带高压形成和变异的动力学问题. 北京: 科学出版社.

(本文编辑汪海英)

基金项目国家重点基础研究发展计划课题(2010CB951903)，国家自然科学基金项目(61361120098、51190101)资助.

作者简介张涛，男，1988年生，博士研究生，主要从事科学计算研究. E-mail: slnazhangtao@gmail.com *通讯作者薛巍，男，1974年出生，副教授，主要从事科学计算研究.E-mail：xuewei@mail.tsinghua.edu.cn

doi:10.6038/cjg20160206 中图分类号P461

收稿日期2014-06-16，2015-12-23收修定稿

Quantification and optimization of parameter uncertainty in the grid-point atmospheric model GAMIL2

ZHANG Tao1,2, XIE Feng3, XUE Wei1,2*, LI Li-Juan3, XU Hao-Yu1, WANG Bin2,3

1DepartmentofComputerScienceandTechnology,TsinghuaUniversity,Beijing100084,China2CenterforEarthSystemScience,MinistryofEducationKeyLaboratoryforEarthSystemModeling,TsinghuaUniversity,Beijing100084,China3StateKeyLaboratoryofNumericalModelingforAtmosphericSciencesandGeophysicalFluidDynamics,InstituteofAtmosphericPhysics,ChineseAcademyofSciences,Beijing100029,China

AbstractPhysical parameterization is one of the most important sources of uncertainties in the current climate system models. With the increasing complexity of models and the diverse requirements for climate studies, the priori and manual model tuning method for physical parameterization has become a bottleneck to further improve the climate system model. In this study, we propose a “two-step” parameter optimization approach. In the first step, an improved full factor sampling scheme is presented to determine the area where the optimal solutions are likely to be found. In the second step, the simplex downhill algorithm is used to perform the search with low computational costs. When applying this “two-step” method to GAMIL2, the grid-point atmospheric model of LASG (State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics), IAP (Institute of Atmospheric Physics), three important parameters from deep convection scheme and cloud fraction scheme are tuned to improve the model performance measured by a comprehensive metrics based on precipitation, wind, temperature, humidity, potential height as well as radiation flux fields. Results show that the proposed metrics is improved by 7.5% compared with the standard GAMIL2 version using our proposed optimization method. The optimal parameters improve the condensation efficiency, leading to reducing the simulated bias of moisture and cloud fraction. Meanwhile, the adjustment of condensation further affects the simulation of temperature, geopotential height, and wind.

KeywordsClimate system model； Physical parameterization scheme； Uncertainty quantification； Optimization algorithm； Mechanism analysis

张涛, 谢丰, 薛巍等. 2016. 格点大气环流模式GAMIL2参数不确定性的量化分析与优化.地球物理学报，59(2):465-475,doi:10.6038/cjg20160206.

Zhang T, Xie F, Xue W, et al. 2016. Quantification and optimization of parameter uncertainty in the grid-point atmospheric model GAMIL2.ChineseJ.Geophys. (in Chinese),59(2):465-475,doi:10.6038/cjg20160206.