基于供应链的汽车零部件集配中心选址模型问题

严南南，章　丽

(上海海事大学科学研究院物流研究中心, 上海201306)



基于供应链的汽车零部件集配中心选址模型问题

严南南，章丽

(上海海事大学科学研究院物流研究中心, 上海201306)

摘要：针对汽车零部件集配中心的选址问题，考虑供应链中三个成员的利益，以汽车零部件集配中心的选址成本与运输成本最小化、零部件供应商运输过程中零部件货损量最小化、整车厂(RDC)满意度最大化作为选址目标，引入零部件在集货配送中货损的微分方程以及模糊预约时间理论，构建基于供应链利益共享的零部件集配中心选址的多目标决策模型。并运用模糊集理论，对目标函数进行处理，再用Matlab软件对该模型进行求解，得到最佳的选址方案，进而用实例验证该模型的有效性。

关键词：供应链成员利益；多目标决策模型；集配中心选址；模糊隶属度函数

0引言

随着经济和社会的快速发展，物流早已被称为第三利润来源，但实际情况确实是物流成本仍然占一半以上的产品成本，成为制约经济发展的一大障碍，而配送中心又是物流系统的一个组成部分。配送中心是专门提供物流配送服务的地点，根据客户订单所需的货物做好准备，包括进行接收、分拣、包装、存储和信息处理等操作，准确、快捷、低成本的进行集货配送的物流设施。它是物流网络中的重要节点，直接与供应商和客户联系，可以直接展示物流服务的质量。而且配送中心位置的选择在物流系统的优化决策问题中也具有着重要的战略意义。

由于配送中心选址问题的重要意义，国内外学者着手研究不同方向的物流配送中心选址问题，并且在理论和实践方面都取得了很高的成就。Yurimoto等[1]建立了以配送的总成本最低为目标函数的数学模型研究物流配送中心选址问题，其中配送费用包括运输费用和设备的运行成本。Sun等[2]学者针对顾客利益和物流计划量部分，通过最低成本确定最优选址方案，再最大限度的减少客户的成本来降低平衡需求。宋少忠[3]针对配送中心选址建立了配送网络综合最小费用模型，并采用鲍摩—瓦尔夫法、表上作业法对多集配中心的数量、选址位置和规模进行求解。汤希峰等[4]针对物流中心选址，将可靠性作为衡量配送中心系统可靠性的一种计算方法，构建了以最小化物流成本和物流服务可靠度最大化为目标的配送中心选址的多目标决策模型，并利用贪婪算法求解，为配送中心选址决策提供更全面的方向。关菲等[5]借鉴现有配送中心选址模型，建立了在模糊环境下以物流的总费用最少，配送中心综合服务水平最高为目标的多目标决策模型，并用粒子群优化算法进行求解。方丽娟[6]考虑时间窗的情况下，提出了基于JIT的汽车零部件集配中心选址模型，并用LINGO求解论证。隋葳葳等[7]构建了以综合运输成本最低为约束条件的物流配送中心选址模型，并用启发式算法求解模型；赵常朋[8]引入模糊隶属函数对客户满意度进行评估，在此基础上构造了基于客户满意度的配送路线优化模型，并运用节约算法解决该问题。蒋利军[9]引入模糊预约时间的隶属函数对顾客满意度进行表示，提出了以顾客满意度最大化为目标的配送中心的选址模型，并运用逐步宽容约束法寻求该模型的最佳解决方案。胡鲜[10]基于供应链成员的利益，运用模糊预约时间和食品消耗量的微分方程，建立了以选址成本和配送成本最小化、运输途中食品的质量损失最小、零售商的满意度最大化为目标的冷链配送中心选址的多目标优化模型，并用运筹学的方法来求解问题。Anjali[11]针对不确定因素下的城市配送中心的选址问题，采用多目标决策方法，先对备选地点进行了解，制定相应的评价标准，再用模糊理论对其无量纲化，运用模糊理想点法对最优解进行评价。马龙飞等[12]考虑需求不确定下物流集配中心的选址问题，将随机需求变量带入离散模型，并用随机规划理论及遗传算法进行求解。Cheng等[13]用模糊预约时间及遗传算法求解了配送中车辆路径规划问题。任永昌等[14]采用模糊决策分析方法研究配送中心选址问题，建立影响因素指标体系等对方案进行决策，证明了该方法具有一定的理论和实践价值。Jacek等[15]运用多准则决策法建立配送中心选址模型并求解；Walter等[16]提出了双层优化模型的物流中心选址，模型假设配送中心可能受到拥堵，由用户对供应限制的期望均衡模型，旨在应用解决自然灾害的受害者提供救济品灾害管理的反应阶段。

通过对已有文献的研究可知，研究选址的文献很多，但研究配送中心选址的文献并不多，研究重工业类型包括汽车零部件集配中心选址的文献更少，而这些研究的共同点是考虑在一定的物流服务水平下物流系统各个环节的花费，再采用不一样的模型和算法得出使总成本最低的最佳解，进而得到最佳选址方案，虽考虑产品的质量及服务质量，但均是分开考虑。而在当今时代的供应链中，成本并不是衡量供应链效率的唯一指标。因此，本文从供应链中三个成员的利益角度出发，使得零部件集配中心以尽可能小的成本实现最大可能的服务水平，即确保供应商在运输途中的零部件货损率最小，又保证整车厂(RDC)的满意度最大，将三个供应链成员利益的最优作为选址的目标，得出最优的零部件集配中心选址的多目标规划模型，引入模糊隶属函数对目标函数进行处理，运用运筹学方法进行求解，并针对实际案例进行分析计算，得出最优值。

1供应链环境下集配中心选址模型的构建

1.1假设条件

为了很好地限定研究的范围并尽量简化研究问题以便建立相关模型，对本文中汽车零部件集配中心的选址问题中涉及到的一些成本及因素，特意假设：

①选址仅考虑在一定的备选地范围内进行，选址模型不考虑超出范围内的选址方案；

②短时期的零部件供应商已定，变化的可能性不大，即使出现，也只是个别情况；

③供应商的地理位置按区域划分，供应商的供货量按区域总计，发货量随时间变动，但可以对集配中心的货物流通量进行预测估计；

④对配送的零件品种不做区分；

⑤运输中的单位运费只采用单一费率，不会根据运输距离的远近而采用多路段定价；

⑥集配中心的运营管理费用可以事先预测；

⑦零部件配送途中，货损量与配送距离成正比，呈线性关系；

⑧零部件配送均用集装箱运输车进行输送；

⑨整车厂(RDC)的需求量是固定的，可预测，且为常量；

⑩一个整车厂(RDC)只能由一个集配中心来满足需求；

1.2多目标规划函数

基于供应链中供应商、集配中心和整车厂(RDC)三方的利益考虑，建立以下多目标规划模型。

1.2.1集配中心的总成本

集配中心的总成本包括零部件集配中心的建立成本(集装箱运输车的购置成本、土地购置成本、建设成本、年运营管理成本)和配送成本，可得：

(1)

式中：I为零部件供应商i的集合；J为零部件集配中心备选地址j的集合；K为整车厂k的集合；o为集装箱运输车的购置单价；λ为单位面积集配中心平均购置集装箱运输车的数量；pj为零部件集配中心j的单位面积土地购置费；q为单位面积集配中心的建设费；f为单位面积集配中心设施设备的购置费；S为零部件集配中心的面积；h为设施设备年折旧率；u为单位面积集散中心的运营管理费；w为单位距离单位数量零部件运费费率；Lij为供应商i到集配中心j的运输距离；Ljk为集配中心j到整车厂(RDC)k的运输距离；Ni(0)为供应商i的初始年零部件供应量；Nk为整车厂k的年零部件需求量。

1.2.2供应商在运输途中的货损量

零部件在运输途中由于撞击等原因，不可避免会产生坏损，运输时间越长货损的概率越大，随着时间的推移货物损坏率呈现指数的增长，所以先以从供应商i向零部件配送中心j配送零部件为例，以初始集货配送的完好的零部件Ni(0)为标准，则零部件货损的微分方程为：

得到初始应装车的零部件数量为：

Ni(0)=eθTijNi,

同理，从零部件集配中心j向整车厂(RDC)k配送零部件时，零部件的货损微分方程和初始应装车的零部件数量如下：

可知运输途中的零部件货损数量包括供应商i到集配中心j的货损量和集配中心j到整车厂(RDC)k的货损量，即：

(2)

式中：Ni为供应商i的年零部件供应量；θ为集货配送途中零部件的货损率；v为集装箱运输车的平均运输速度；Tij为供应商i到集配中心j的运输时间；Tjk为集配中心j到整车厂(RDC)k的运输时间；Rij为供应商i到集配中心j的运输途中的堵车风险；Rjk为集配中心j到整车厂(RDC)k的运输途中的堵车风险。

1.2.3整车厂(RDC)的满意度

由于汽车零部件配送物流是一种对准时性要求很高的物流活动，实际问题中，整车厂(RDC)要求配送服务要在订单下达之后的某个时间段进行，当汽车零部件集配中心无法满足整车厂(RDC)在准时性上的配送要求时，整车厂(RDC)对汽车零部件集配中心的满意度将大大降低。因此引入模糊预约时间理论表示整车厂(RDC)的满意度。

可得：

(3)

多目标规划函数的约束条件如下：

(4)

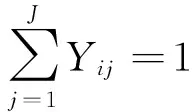
(5)

(6)

Yij≤Xj,

(7)

Zjk≤Xj,

(8)

Ni(0)≥Nk,

(9)

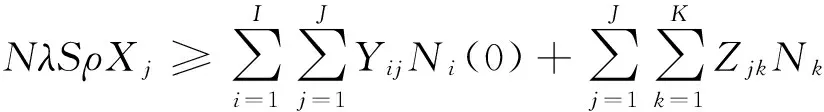
(10)

N为每辆集装箱运输车单次运输的最大容量；ρ为每辆集装箱运输车的年输送次数；χ为零部件集配中心的建设数量上限。目标函数(1)要求零部件集配中心的建立成本(包含集装箱运输车的购买成本、土地的购买成本、配送中心的建设成本、设施设备的购买成本、零部件集配中心j的年运营管理成本等)和从供应商到集配中心再到整车厂(RDC)的集货配送成本的总和最小；目标函数(2)要求从供应商到零部件集配中心再到整车厂(RDC)的运输途中零部件货损率最小；目标函数(3)要求整车厂(RDC)对零部件集配中心的服务满意度最大。约束条件(4)表示至少选址一个零部件集配中心，并且不超过χ个；约束条件(5)表示每个供应商的零部件产品由一个零部件集配中心负责配送；约束条件(6)表示每个整车厂(RDC)的零部件产品由一个零部件集配中心负责配送；约束条件(7)表示只在j处选址建立集配中心，才与供应商有供应关系；约束条件(8)表示只在j处选址建立了集配中心，才与整车厂(RDC)有配送关系；约束条件(9)表示供应商的年供货量不小于整车厂(RDC)的年需求量；约束条件(10)表示各个零部件集配中心向供应商接收及向整车厂(RDC)配送的汽车零部件的总量应该小于零部件集配中心的配送能力。

2多目标选址模型求解

由于本文的第三个目标函数整车厂(RDC)满意度的求解运用了模糊隶属函数，所以运用模糊数学理论对其他目标函数进行模糊化处理，对三个目标函数都进行标准化处理，最后运用运筹学的线性功效系数法求解该模型。

2.1求解单个目标函数的最优值

目标函数转化为：

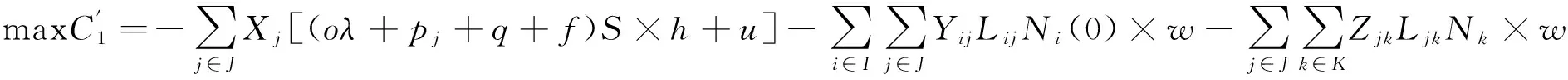
(11)

(12)

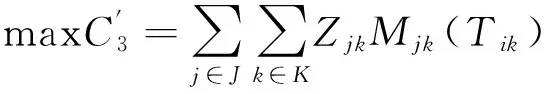
(13)

2.2确定模糊目标集

综上得到：

3案例分析

某第三方汽车零部件物流企业A公司计划建设零部件集配中心，配送中心定位为服务特定的几个整车厂的汽车零部件集配中心。经过公司老员工的认知经验考虑后，锁定在E1(外高桥港区)，E2(吴淞口港区)，E3(洋山港保税区)这3个备选地址，选定其中一个建立汽车零部件集配中心。目前该第三方物流公司服务的客户主要是汽车零部件供应商和整车厂(RDC)，其中供应商按区划分为F1(宁波)，F2(南京)，F3(常熟)，F4(浦东)，F5(嘉定)，F6(闵行)这六个区域，以及H1(武汉)，p(烟台)，p(沈阳)，h1(上海金桥)共4个整车厂，为了方便，下文均以字母表示。该第三方物流企业在建立零部件集配中心之前与上下游供应商和整车厂达成了合作意向，即该零部件集配中心选址要在一定程度上考虑供应商和整车厂的利益，即在尽可能小的集配中心选址和运营成本下，尽可能令供应商的零部件在运输途中的货损率最小以及整车厂对配送的满意度最大。供应商和整车厂所在地以及集配中心选址的备选地址见图1～图4。集配中心j选址相关参数值，土地购置费，集配中心j到整车厂(RDC)k的运输距离以及运输堵车风险Rjk见表2～表4；供应商i的相关参数见表5～表7；整车厂(RDC)的相关参数见表8和表9。

图1供应商分布

Fig.1Supplier distribution

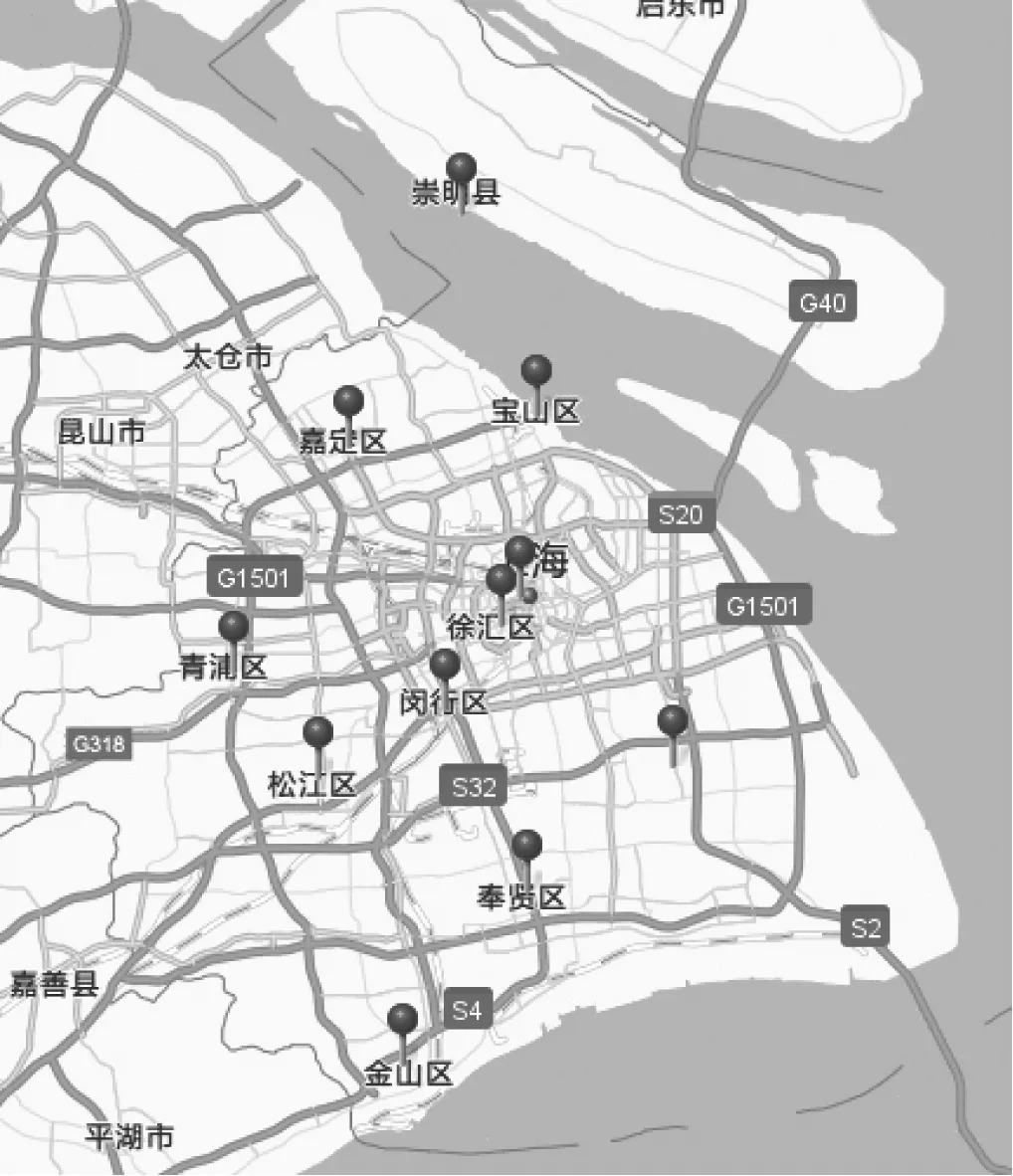
图2上海供应商分布

Fig.2Shanghai supplier distribution

图3　整车厂分布

Fig.3　The distribution of the vehicle factory

图4　备选地址分布

表2　零部件集配中心j的土地购置费

表3　集配中心j到整车厂(RDC)k的运输距离

表4　零部件从集配中心j到整车厂(RDC)k的运输路途堵车风险Rjk

表5　供应商i到集配中心j的运输距离

表6　供应商i的年供应量Ni

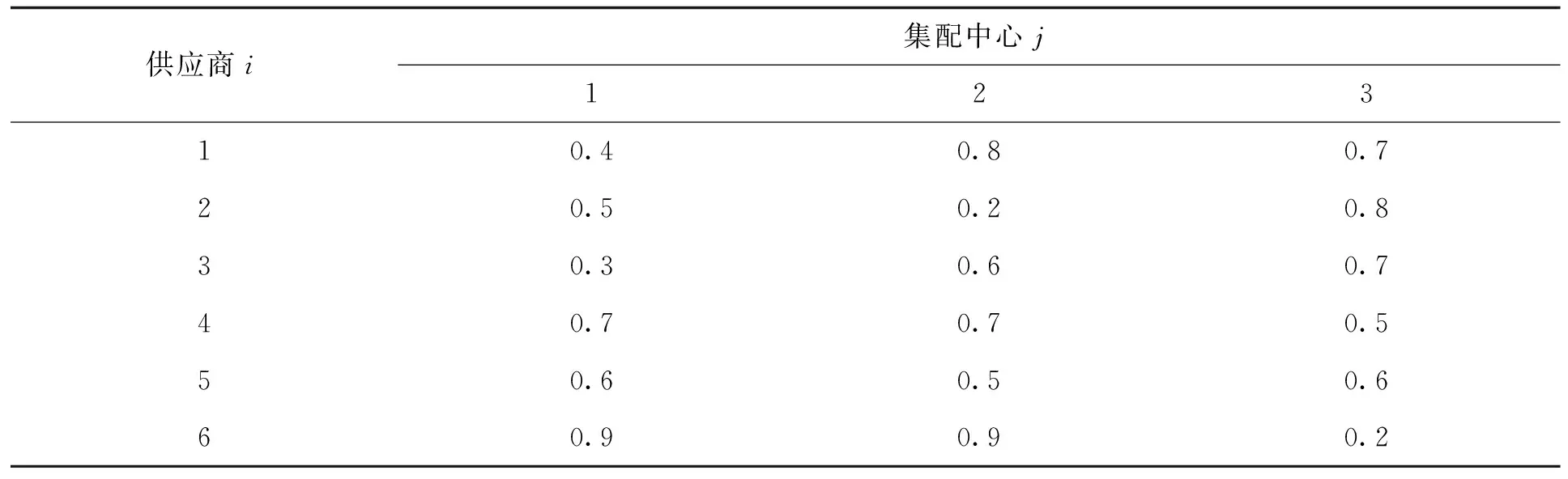
表7　零部件从供应商i处到集配中心j的运输路途堵车风险Rij

表8　整车厂(RDC)的年需求量Nk

表9　整车厂(RDC)k可接受及期望的配送时间范围

将表1～表9的数据代入式(11)～式(13)，并用Matlab编程计算可得：

在获得三个目标函数的最优值和最次值的情况下，由于多目标规划的解的函数值必须在最优值和最次值的上界和下界之间。通过上述的求解方案，构造这三个目标的伸缩指标：

α1=-5.006 6×1010-(-6.154 0×1010)=1.147 4×1010,

α2=-1 815 500-(-9 424 200)=7 608 700,

α3=3.576 7-0.252 6=3.324 1。

于是得到目标函数的模糊约束条件为：

分别构建这三个目标函数的模糊极大集：

令M=M1∩M2∩M3，求解β在M集合中的极大值，原多目标规划模型转化为求解下列方程：

用Matlab得出3个备选地址的目标函数值如表10所示。

表10　汽车零部件集配中心选址目标函数结果

从表10中可以看出，如果只将选址及配送成本总和成本最小作为选址目标，那么最佳地点是E2；只将零部件的在途损失量最小作为选址目标，那么最佳地点是E1，只将整车厂(RDC)的满意度最大作为选址目标，那么最佳地点是E1。

4结语

本文在考虑了现有物流配送中心选址问题及其模型的基础上，从汽车零部件物流供应链中供应商、集配中心和整车厂三方的利益考虑，综合考虑了集配中心选址成本及配送成本、在途运输中的零部件货损量和整车厂(RDC)满意度三个方面，将其作为选址目标，建立多目标规划模型，运用模糊集理论对目标函数进行处理，构建隶属度函数，并用Matlab进行求解。然后用企业A的实际情况论证该模型，考虑了不同地址对配送中心成本、供应商在途货损和整车厂(RDC)满意度的影响，选出了合适的地址，从供应链成员利益角度为集配中心的选址提供了新方法。

当前的集配中心选址多数只单独考虑物流成本最小化、客户的满意度最大化、货损的最小化，或者考虑其中的两个方面，有的依据其中一点建立奖励惩罚目标函数。而本文考虑了三个选址目标，考虑的更加全面，也更加适应当今物流市场利益共享的发展潮流，对其他汽车零部件集配中心的选址及汽车物流的发展有一定的实际参考意义，极大的满足了汽车零部件市场日益增长的高标准物流需求的要求。

由于本文只考虑了确定需求下的集配中心选址以及供应链中的三个主体，未来的研究可以考虑随机需求下的集配中心选址，或者是把供应链中更多成员的利益纳入选址决策模型，这些都有待进一步研究。

参考文献：

[1]YURIMOTO S, KACAYAMA N.A model for the optimal number and locations of public distribution centers and its application to the Tokyo metropolitan area[J]. International Journal of Industrial Engineering.Theory Applications and Practice, 2002,9(4):363-371.

[2]SUN H J, GAO Z Y, WU J J.A bi-level programming model and solution algorithm for the location of logistics distribution centers[J]. Applied Mathematical Modelling, 2008, 32(4): 610-616.

[3]宋少忠.汽车零部件入厂物流链建设中的若干问题研究[D]. 长春：吉林大学,2012.

[4]汤希峰,毛海军,李旭宏.物流配送中心的多目标优化模型[J]. 东南大学学报,2009,39(2): 404-407.

[5]关菲，张强.模糊多目标物流配送中心选址模型及其求解算法[J]. 中国管理科学,2013,21(SI):57-62.

[6]方丽娟.基于JIT的汽车零部件供应物流配送中心选址问题研究[D]. 武汉：华中科技大学,2012.

[7]隋葳葳，宋现允，付蕾.物流配送中心选址数学模型的算法问题研究[J]. 物流技术，2013，32(6)：157-159.

[8]赵常朋.基于客户满意度的物流配送中心路线优化研究[D]. 重庆：重庆交通大学,2009.

[9]蒋利军.基于顾客满意度的配送中心选址问题研究[D]. 成都：西南交通大学,2005.

[10]胡鲜.供应链环境下的食品冷链配送中心选址研究[D]. 北京：北京交通大学,2011.

[11]ANJALI A.A multi-criteria decision making approach for location planning for urban distribution centers under uncertainty[J]. Mathematical and Computer Modelling, 2011,53(1-2):98-100.

[12]马龙飞,毕蕾.基于随机需求的配送中心选址离散模型研究[J]. 物流科技,2010,33(1):24-27.

[13]CHENG R, GEN M.Vehicle routing problem with fuzzy due-time using genetic algorithms[J]. Japanese Journal of Fuzzy Theory and Systems, 1995, 7(5):1050-1061.

[14]任永昌,刑涛,赵国强.物流配送中心选址方案模糊决策分析[J]. 辽宁工程技术大学学报,2010,29(3):517-520.

[15]JACEK Z, SZYMON W. The selection of the logistics center location based on MCDM/A methodology[J]. Transportation Research Procedia, 2014(3): 555-564.

[16]WALTER J, NADA D. Bi-objective bilevel optimization of distribution center locations considering user equilibria[J]. Transportation Research Part E, 2016(85): 1-22.

(责任编辑梁碧芬)

收稿日期：2016-03-01；

修订日期：2016-04-11

基金项目：国家自然科学基金资助项目(71071093)；上海市科委科技创新项目(12595810200)

通讯作者：严南南(1968—)，女，湖北鄂州人，上海海事大学副教授，博士；E-mail:nnyan68@163.com。

doi:10.13624/j.cnki.issn.1001-7445.2016.0836

中图分类号：F252.8;F224

文献标识码：A

文章编号：1001-7445(2016)03-0836-11

Research on auto parts distribution center location model based on supply chain

YAN Nan-nan，ZHANG Li

(Logistics Research Center, Shanghai Maritime University, Shanghai 201306, China)

Abstract:For the auto parts distribution center location problem，based on the interests of the three members in the supply chain, in order to minimize location cost and transportation cost of the automobile parts distribution center and the amount of damaged parts in the process of transportation, and to maximize the satisfaction of vehicle plant (Regional distribution center), a multi-objective decision model for auto parts distribution center location based on benefit sharing in supply chain has been established, which introduces differential equations for parts damage in transportation and fuzzy due-time theory. Fuzzy set theory is used to process the objective function, and then the model is solved by Matlab software, thus the optimal location comes out. The model is verified by an example.

Key words:benefits of supply chain members; multi-objective decision model; distribution center location; fuzzy membership function

引文格式： 严南南，章丽.基于OpenGL的ArcGIS Globe动态三维符号渲染可视化研究[J].广西大学学报(自然科学版)，2016，41(3)：836-846.