碳汇木材复合经营对杉木人工林经济成熟龄及现值收益的影响

巢　林, 刘艳艳, 洪　伟,3, 吴承祯,3,4, 林　卓

(1.福建农林大学林学院，福建 福州 350002；2.中国科学院沈阳应用生态研究所，辽宁 沈阳 110016；3.福建省高校森林生态系统过程与经营重点实验室，福建 福州 350002；4.武夷学院生态与环境学院，福建 武夷山 354300)



碳汇木材复合经营对杉木人工林经济成熟龄及现值收益的影响

巢林1, 刘艳艳2, 洪伟1,3, 吴承祯1,3,4, 林卓1

(1.福建农林大学林学院，福建 福州 350002；2.中国科学院沈阳应用生态研究所，辽宁 沈阳 110016；3.福建省高校森林生态系统过程与经营重点实验室，福建 福州 350002；4.武夷学院生态与环境学院，福建 武夷山 354300)

摘要:以中亚热带杉木中心产区为案例，基于样地调查数据、前人有关模型及相关经济技术指标，采用年均净现值法研究碳汇木材复合经营目标下杉木人工林经济成熟龄及现值收益，探讨了立地质量、木材及碳价格、森林经营成本、利率等因素变化对经济成熟龄及现值收益的影响.结果表明：在地位指数为16 m、利率为5%、碳价格为42.41元·t-1的条件下，杉木人工林经济成熟龄为19 a，年均碳汇木材复合收益最大值max(ANPVw+c)为1 695.5元·hm-2.回归分析发现，碳汇木材收益净现值NPVw+c和ANPVw+c与林龄之间分别呈现出Sigmoid函数、三次函数关系；增加碳汇目标并未对经济成熟龄产生影响，但现值收益max(ANPVw+c)增加幅度为7.34%～9.96%；地位指数从8 m指数级增加到24 m指数级，经济成熟龄由25 a提前至16 a，max(ANPVw+c)由225.3元·hm-2增加到5 680.1元·hm-2；木材价格每上涨或降低5%，max(ANPVw+c)上升或下降5.65%～9.97%；营林成本每上涨或降低5%，max(ANPVw+c)下降或上涨2.01%～4.84%；经济成熟龄随利率水平的提高而不断提前，max(ANPVw+c)则逐渐下降，利率每提高1%，max(ANPVw+c)下降13.66%～20.04%；碳价格从0增加至800元·t-1，经济成熟龄提前1～3 a，max(ANPVw+c)增加2.39～2.94倍，碳价格每提高一个价位，max(ANPVw+c)平均增加11.55%～14.53%.表明增加碳汇经营目标对现值收益有较大影响，木材收益目标和碳汇收益目标可以兼容，为开展人工林碳汇经营、发挥人工林巨大的碳汇潜力以及增加林业经营者的收益等提供重要依据.

关键词:森林经营学; 碳汇木材复合经营; 年均净现值; 现值收益; 经济成熟龄; 森林碳汇; 杉木

采伐年龄是影响森林现值效益的重要因素之一，确定森林木材资源最佳收获时间是森林资源经济学领域研究的热点问题之一，从经济成熟角度确定轮伐期长期倍受经济学家和森林培育学家的关注，也是一个非常具有挑战性的课题[1，2].基于Samuelson对于这一问题的开创性研究[3]，大多数经济学家认为净边际效益低于当前利率时森林木材资源达到最佳采伐年龄.国外，在确定森林采伐收获年龄时，将森林碳汇价值融入森林最优轮伐期确定的研究，以期在同时考虑木材收获和碳汇价值的情况下，获得最优的林分管理策略[4-9].

杉木(Cunninghamialanceolata)是我国重要的人工用材林树种，其面积和蓄积在人工林中所占的比例最高，在我国林业发展中占有极其重要的地位，因此确定其最佳采伐年龄具有重大意义与实践价值.为此，前人运用不同技术方法对杉木人工林的最优轮伐期的确定做了大量研究，取得了很多有价值的成果[10-15].杉木人工林面积居我国人工林面积首位，在确定其经济成熟龄时，同时考虑到碳汇收益，对于转变森林经营方式、提出最佳森林经营决策、应对全球气候变化以及实现减排目标等具有重大意义.近年来，一些学者开始重视杉木人工林的碳汇价值[16-18]，考虑杉木人工林的碳汇收益及其对经营采伐决策的影响成为当前研究的热点问题.然而，在生长收获预估模型的基础上，通过建立碳汇木材复合收益模型确定杉木人工林经济成熟龄的研究尚未见有报道.本研究依据杉木人工林林分生长预估模型和碳收获量模型，采用年平均净现值法，确定碳汇木材复合经营目标下杉木人工林经济成熟龄，研究碳汇木材复合经营对杉木人工林经济成熟下现值收益的影响，比较木材收益单一经营目标与碳汇木材复合经营目标下经济成熟龄及现值收益的差异性，探讨立地质量、木材价格、森林经营成本、利率以及碳价格等因素对经济成熟龄及现值收益的贡献，以期为杉木人工林经营方式的转变、经营决策的优化、提高林业经营者的收益以及推行碳汇林经营等提供依据.

1研究区概况

研究地设于三明市将乐县金森林业股份有限公司经营的杉木人工林栽培区，该区域位于中亚热带季风气候区，东经117°05′～117°40′，北纬26°26′～27°04′.境内地形复杂多样，以低山和丘陵为主，年平均气温18.7 ℃，年平均降水量1 698.2 mm，无霜期295 d，年平均相对湿度82%，主导风向为东南风.土壤具有典型的中亚热带地带性土壤特征，山地土壤分布具有垂直地带性，随着海拔的升高土壤类型分布依次是红壤—黄红壤—黄壤—山地草甸土.地带性植被属中国东部温润森林区亚热带常绿阔叶林，植物种类丰富.

2研究方法

2.1数据收集

在金森林业股份有限公司经营的杉木人工林栽培区调查441块杉木人工林临时标准地，每块标准地666.67 m2，测定杉木胸径、树高等测树因子.为了计算杉木人工林经济成熟龄，参考金森林业股份有限公司2011-2015年森林经营方案，调查收集了木材价格、营林生产成本、木材生产有关税费等主要技术经济指标.木材价格：规格材1 200元·m-3，非规格材1 100元·m-3.杉木营林费用为9 370元·hm-2(包括林地清理、整地、施肥、栽植、补植、苗木款、挖管茅、肥料苗木运输费、管理费等).税费按木材起征价征收，其中杉木规格材为500元·m-3，非规格材为390元·m-3.育林费按木材统一计征价的10%计取.森林植物检疫费按木材销售价的2‰计取.伐区设计费按每立方米木材(出材)7.2元计取.木材检尺费按每立方米木材(出材)13元计取.防洪费按木材销售价的0.7‰征收.年均病虫害防治费29.99元·hm-2，年平均森林管护费89.96元·hm-2，年均林地使用费149.93元·hm-2，木材采集运输费用150元·m-3.销售费用按销售收入的2%提取.管理费用含管理人员工资，按销售收入的10%提取.

2.2模型设计

2.2.1地位指数模型林分优势木平均高采用杉木人工林Sloboda树高生长模型估计[19]：

(1)

式中：H优为优势木平均高；SI为立地指数；Xs为杉木人工林标准年龄(20a)；t为林龄.

2.2.2蓄积量模型将N、D和H代入福建省杉木二元材积方程[14,20]，计算杉木人工林林分蓄积量，由此得到蓄积量模型：

M=N·V=N·0.000 087 2D1.785 388 607H0.931 392 369 7

(2)

式中，M为林分蓄积量；N为林分密度；V为单株材积；D为林分平均胸径；H为林分平均树高.

2.2.3平均胸径及平均树高模型通过对试验数据的模拟，建立平均胸径和平均树高模型：

H=0.938 8H优-2.567 7，R=0.998 1

(3)

(4)

式中，H为林分平均树高；H优为优势木平均高；D为林分平均胸径；N为林分密度；A为林分年龄.

2.2.4林分出材率模型林分出材率计算选择陈则生[15]建立的杉木人工林林分材种出材率模型：

P1=100.812 4e-306.703/(D·H)，R=0.896 4

(5)

P2=77.988 64e-0.002 59(D·H)，R=0.873 7

(6)

式中，P1为林分规格材出材率；P2为林分非规格材出材率；D为林分平均胸径；H为林分平均高.

2.2.5碳收获量模型采用黄贤松等[21]提出的杉木人工林碳收获量预估模型，计算不同林龄林分的碳贮量，其模型表达式为：

C=932.56D0.095 4H0.198SDI-0.090 3M，R=0.978

(7)

2.3经济成熟龄及现值收益的计算

运用净现值(NPV)法和年均净现值(ANPV)法计算杉木人工林的现值收益.NPV和ANPV达到最大时的林龄为杉木人工林的经济成熟龄，其计算公式为[14]：

(8)

(9)

式中：NPVw为木材收益净现值；ANPVw为年均木材收益净现值；t为林龄；Rt表示t年时的收入；Ct表示t年时的费用支出；P为贴现率.

碳收获成熟龄为杉木人工林碳汇收益最大时的年龄，即碳汇经济成熟龄，其计算公式为：

(10)

(11)

式中：NPVc为碳收益净现值；ANPVc为年均碳收益净现值；t为林龄；C为林分碳贮量；Pc表示碳价格.本研究中碳价格取欧盟碳交易市场和中国碳交易市场碳交易成交价的均值进行计算，为42.41元·t-1；P为贴现率.

碳汇木材复合经营目标下，杉木人工林经济成熟龄为木材收益和碳收益之和最大时的林龄，计算公式表示如下：

NPVw+c=NPVw+NPVc

(12)

ANPVw+c=ANPVw+ANPVc

(13)

式中：NPVw+c为碳汇木材复合收益净现值；NPVw为木材收益净现值；NPVc为碳收益净现值；ANPVw+c表示年均碳汇木材复合收益净现值；ANPVw为年均木材收益净现值；ANPVc为年均碳收益净现值.

2.4数据处理

所有数据采用Excel2007软件统计绘制，木材和碳汇净现值收益与林龄的回归关系分析利用Sigmaplot12.5软件完成.

3结果与分析

3.1碳汇木材复合经营下杉木人工林经济成熟龄及现值收益的计算

在地位指数为16m、利率为5%、碳价格为42.41元·t-1的条件下，年均木材收益净现值(ANPVw)以及复合经营目标下碳汇木材复合收益年均净现值(ANPVw+c)的计算结果如表1所示.

由表1可知，仅考虑木材收益时，采用净现值法(NPVw)计算出其经济成熟龄为33a， NPVw为43 838.5元·hm-2.而采用年均净现值法(ANPVw)确定的经济成熟龄为19a，ANPVw为1 695.5元·hm-2，地位指数由8m指数级增加至24m指数级.采用NPVw确定的经济成熟龄由36a提前至31a.

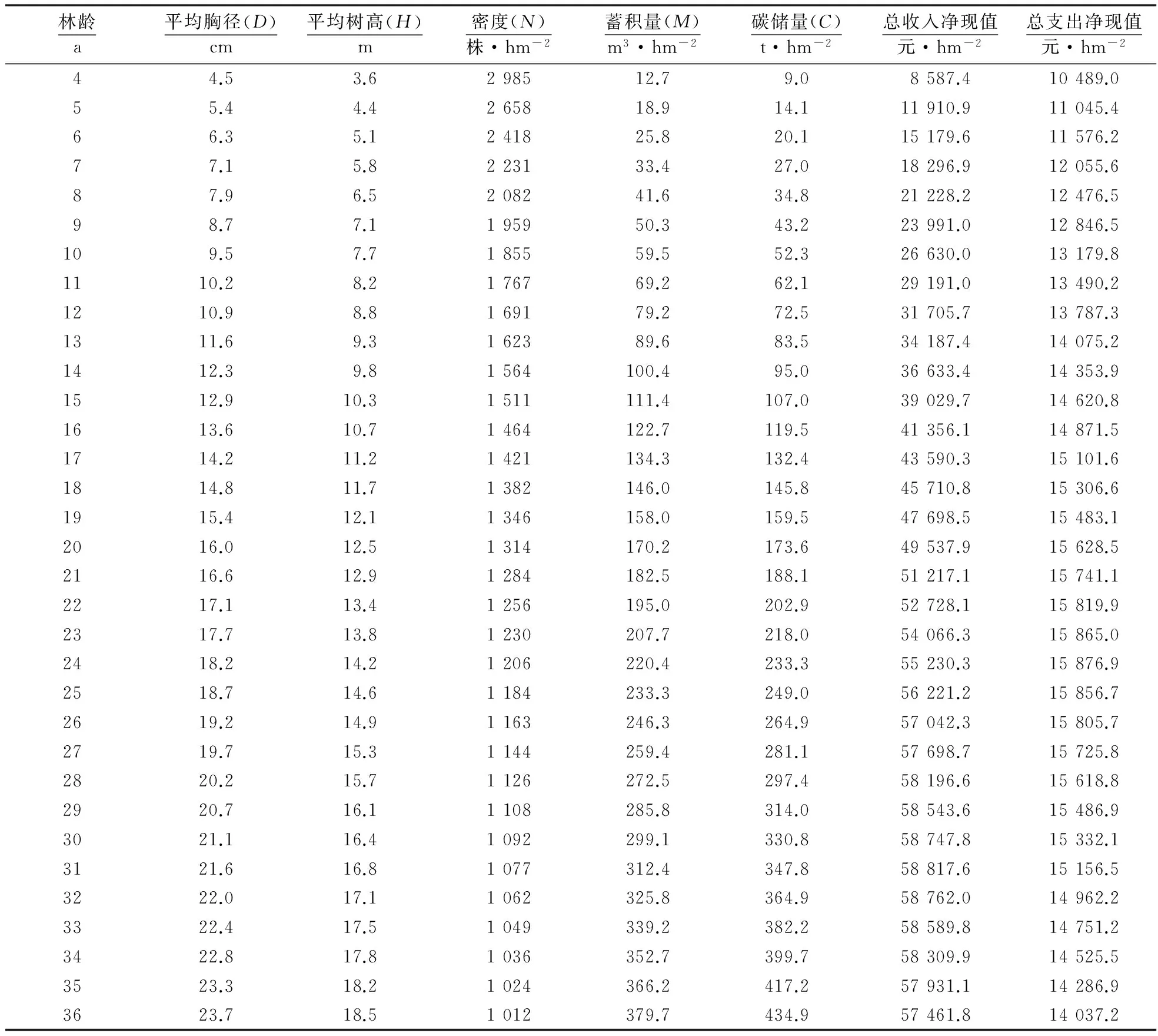
表1　杉木人工林经济成熟龄及现值收益

续表1

采用ANPVw确定的经济成熟龄从25 a提前到16 a.指数级为16 m时，在碳汇木材复合经营目标下，依据NPVw+c和ANPVw+c确定的经济成熟龄仍然为33和19 a，但NPVw+c和ANPVw+c分别达到47 078.4和1 837.3元·hm-2，与木材单一经营目标相比，现值收益分别提高了7.39%和8.36%.8～24 m地位指数级下，增加碳汇目标均未对经济成熟龄产生任何影响.不同立地指数下，碳汇木材复合经营目标下max(NPVw+c)和max(ANPVw+c)与木材收益单一经营目标下max(NPVw)和max(ANPVw)相比分别提高了7.01%～8.87%和7.34%～9.96%.由此可知，增加碳汇目标能够显著提高林农的经济收益.

NPVw、NPVc和NPVw+c变化趋势一致，均随林龄的增加而不断上升，达到某一林龄阶段后上升速度减缓，其变化趋势呈S型曲线.NPVw、NPVc以及NPVw+c随林龄的变化规律可以用Sigmoid函数模型进行很好的表征，显著性检验结果表明模型均达到极显著水平(表2).

ANPVw、ANPVc和ANPVw+c表现出相同的变化规律，ANPVw、ANPVc和ANPVw+c随林龄的增加呈现出中间高两端低的常态分布.在林分生长初期，ANPVw和ANPVw+c均小于0；随着林龄的增加，其值从负值转变为正值，并逐年增加，达到极大值后开始逐年减小.说明在林分生长初期处于盈亏状态；之后盈利随着林龄的增加逐步升高，极大值所对应的林龄为经济成熟龄，此时获得的收益最高.对ANPVw、ANPVc和ANPVw+c与林龄之间的关系采用不同数学模型进行回归分析，结果表明ANPVw、ANPVc和ANPVw+c随林龄的变化规律可以用三次函数进行表征，显著性检验结果表明模型均达极显著水平(表2).

表2　木材和碳汇净现值收益与林龄的关系

3.2立地质量对碳汇木材复合经营下经济成熟龄及现值收益的影响

从表3可以看出，随着地位指数由8 m指数级升到24 m指数级，经济成熟龄呈现出提前的特征规律，其对应的NPVw、ANPVw、NPVc、ANPVc、NPVw+c以及ANPVw+c均呈递增趋势.木材单一经营目标和碳汇木材复合经营目标下，随着地位指数的增加，经济成熟龄由25 a提前至16 a，地位指数每增加2 m，经济成熟龄基本上提前1 a.

表3　不同立地质量下经济成熟龄及现值收益

不同立地质量条件下，max(ANPVw+c)存在较大差异，max(ANPVw+c)由8 m指数级时的225.3元·hm-2增至24 m指数级时的5 680.1元·hm-2；年均净现值收益提高了25倍之多；地位指数每增加2 m，所获得的现值收益增加幅度为25.91%～123.57%.此外，增加碳汇经营目标虽然没有对经济成熟龄产生影响，但所获得的现值收益有所增加.8～24 m指数级下，NPVw为6 197.1～119 950.8元·hm-2，NPVw+c为6 746.5 ～128 363.4元·hm-2.增加碳收益后，现值收益提高了1.07～1.09倍，max(ANPVw)为204.9～5 291.6元·hm-2，与max(ANPVw+c)相比提高了1.08～1.10倍.

3.3经济因素对碳汇木材复合经营下经济成熟龄及现值收益的影响

3.3.1木材价格对碳汇木材复合经营下经济成熟龄及现值收益的影响由图1可知，随着木材价格的上涨，经济成熟龄提前.木材价格上涨5%～30%时，8～14 m指数级经济成熟龄提前2～3 a，16～22 m指数级经济成熟龄提前1 a，24 m指数级经济成熟龄不变；木材价格下降5%～30%时，8～16 m经济成熟龄推迟2～5 a，18～24 m经济成熟龄推迟1 a.

由图2可知，随着木材价格的上涨，max(ANPVw+c)不断增加；而木材价格下降，max(ANPVw+c)减少.随着地位指数由8 m指数级增加至24 m指数级，木材价格每上涨5%，max(ANPVw+c)提高5.65%～8.18%；木材价格每降低5%，max(ANPVw+c)下降6.81%～9.97%.以16 m地位指数级为例，木材价格上涨5%～30%，max(ANPVw+c)从1 836.4元·hm-2增加至2 548.8元·hm-2，提高了38.79%；木材价格降低5%～30%，max(ANPVw+c)由1 836.4元·hm-2减少至1 365.7元·hm-2，下降幅度为25.63%.

3.3.2森林经营成本对碳汇木材复合经营经济成熟龄及现值收益的影响由图3可知，森林经营成本上涨5%～20%，8～14 m指数级经济成熟龄延迟2 a，16 m指数级延迟1 a，18～20 m指数级经济成熟龄保持不变；当森林经营成本上涨30%时，8～14 m指数级经济成熟龄延迟2～4 a，16～24 m指数级经济成熟龄推迟1～2 a；森林经营成本降低5%，8～14 m以及18 m指数级经济成熟龄提前1 a，其余地位指数级经济成熟龄未发生改变；森林经营成本降低15%时，8～14 m指数级经济成熟龄提前2 a，16～22 m指数级经济成熟龄提前1 a；森林经营成本降低30%时，8～14 m指数级经济成熟龄提前3～4 a，16～22 m指数级经济成熟龄仅提前1 a.24 m指数级经济成熟龄并未随着营林成本的变化而变化.

从图4可以看出，随着森林经营成本的不断上涨，max(ANPVw+c)逐渐降低.随着地位指数由8 m指数级增加至24 m指数级，森林经营成本每上涨5%，max(ANPVw+c)平均降低2.01%～4.76%，森林经营成本每降低5%，max(ANPVw+c)平均增加1.43%～4.84%.以16 m地位指数级为例，森林经营成本上涨5%～30%， max(ANPVw+c)从1 836.4元·hm-2降至1 600.8元·hm-2，下降幅度达12.83%；森林经营成本降低5%～30%时，max(ANPVw+c)由1 836.4元·hm-2上升至2 001.9元·hm-2，提高了9.01%.

3.3.3利率对碳汇木材复合经营经济成熟龄及现值收益的影响不同利率水平下的杉木人工林经济成熟龄如图5所示.从图5可以发现，利率的变化对经济成熟龄有显著影响.随着利率的提高，经济成熟龄不断提前.利率每提高1%，不同立地条件下经济成熟龄提前1～6 a；在利率较低时，利率每提高1%，其经济成熟龄变动幅度较大；当利率较高时，经济成熟龄变化程度随利率的变化而变化的程度大大降低，且立地条件差的林分，其经济成熟龄对利率变化更为敏感.在相同利率水平下，立地条件差林分的经济成熟龄比立地条件优越的林分更迟.

从利率变动对碳汇木材复合经营目标下max(ANPVw+c)的影响来看(图6)，以碳价格42.41元·t-1计算，不同立地条件下max(ANPVw+c)随着利率的提高均呈现出降低趋势，地位指数由8 m指数级增加至24 m指数级；利率每提高1%，max(ANPVw+c)下降13.66%～20.04%.以16 m地位指数级为例，利率从3%提高到7%，max(ANPVw+c) 由2 736.1元·hm-2下降至 1 363.7元·hm-2，下降幅度达50.16%.因此，利率变动会对现值收益产生巨大影响.

3.3.4碳汇价格对碳汇木材复合经营经济成熟龄及现值收益的影响为了探讨碳汇价格变化对经济成熟龄及现值收益所产生的影响，设置碳汇价格在0～800元·t-1的变动区间，其中碳价格为0也就意味着仅考虑木材收益单一经营目标.研究发现，不同立地条件下，随着碳价格的增加，经济成熟龄呈现出提前的特征规律(图7).当碳汇价格为100元·t-1时，8～14 m指数级经济成熟龄提前1 a，16～24 m指数级经济成熟龄未发生变化；当碳汇价格提高至200元·t-1时，16～22 m指数级经济成熟龄提前1 a；当碳汇价格为400元·t-1时，8～18 m指数级经济成熟龄提前2 a；之后，碳汇价格由500元·t-1增加至800元·t-1，经济成熟龄变化很小.在目前木材市场价格远高于碳市场价格的情况下，经济成熟龄对碳价格变动不敏感，碳价格在较长的变动范围内并未对杉木人工林经济成熟龄产生十分明显的影响.

从复合经营目标年均净现值最大值max(ANPVw+c)来看(图8)，在利率为5%的水平下，随着碳汇价格的提高，max(ANPVw+c)呈不断增加趋势.地位指数由8 m上涨至24 m，碳汇价格每提高1个价位，max(ANPVw+c)平均增加11.55%～14.53%.以16 m指数级为例，碳汇价格由0元·t-1提升至800元·t-1，max(ANPVw+c)由1 695.5元·hm-2增加至4 394.5元·hm-2，提高2.59倍.

4讨论

木材产量受很多不可控因素的影响，因此，评估人工林的投资效益也具有不确定性[22].采用年均净现值法评价杉木人工林的投资效果存在不确定性，这些不确定性的来源包括调查数据、模拟者所应用的生长与收获模型、木材价格及利率的波动等[23].发挥森林碳汇功能已经成为我国乃至全球应对气候变化的重要策略[16]，森林碳汇具有潜在的生态经济价值，使林业经营者在获得木材收益的同时，还可以得到相应的碳汇收益.

研究发现，在目前经营成本、木材和碳价格以及利率水平下，增加碳汇目标并没有对经济成熟龄产生影响，即森林经营者在碳汇木材复合经营目标下不用改变原来的采伐收获决策.朱臻等[18]指出，这主要是由于碳的市场价格远低于木材市场价格，导致杉木经营者改变最佳轮伐期的机会成本很小，所以木材单一经营和碳汇木材复合经营两类目标下经济成熟龄保持不变.然而，增加碳汇经营目标对杉木人工林的现值收益产生显著影响，地位指数由8 m指数级增加到24 m指数级，碳汇木材复合经营目标比木材单一经营目标下经济成熟时所得的净现值收益提高了7.34%～9.96%，因此，增加碳汇目标有利于增加林业经营者的收入.

碳汇木材复合经营目标条件下，杉木人工林经济成熟龄随着地位指数的增加而提前，地位指数由8 m指数级增加到24 m指数级，经济成熟龄由25 a提前至16 a.地位指数每增减2 m，经济成熟龄总体上提前或推迟1 a.李晨燕[24]对福建柏(Fokieniahodginsii)人工林经济成熟龄进行研究，也发现地位指数变化2 m，福建柏人工林经济成熟龄提前或推迟2 a左右.陈则生[15]研究结果表明，杉木人工林经济成熟龄为17 a，基本上与立地质量无关，这与本研究得出的结论存在差异性.生长于好的立地条件下的杉木人工林的生长速度大于生长在立地条件差的杉木人工林，故随着地位指数的上涨其经济成熟龄应该具有提前的趋势，本研究也验证了这一点.此外，地位指数每增加2 m，经济成熟时所获得的现值收益max(ANPVw+c)平均增幅达52.10%.由此可见，立地质量对杉木人工林的现值收益起着至关重要的作用.

木材市场价格对杉木人工林经济成熟产生反向作用，木材价格上涨，经济成熟龄提前；木材价格降低，经济成熟龄推迟.木材价格升降幅度与经济成熟龄变动程度密切相关.经济成熟龄对森林经营成本变化的响应与其对木材价格变动的反应正好相反，森林经营成本增加，经济成熟龄延迟；经营成本下降，经济成熟龄提前.经济成熟龄随着利率水平的提高而不断提前.在利率水平较低时，经济成熟龄变动幅度要远大于高利率水平时其经济成熟龄变化程度.利率每提高1%，其max(ANPVw+c)平均减少16.07%，可以看出，利率变化对森林经营者的现值收益有着重大影响.朱臻等[16]研究发现，利率每提高1%，杉木轮伐期基本提前1 a，利率从3%提高到7%，林地期望值下降70%～75%，与本研究结果相似.但也存在一定的差异性，一方面是由于采用的计算模型不同，另一方面是因为其计算结果为林地期望值，而本研究计算结果为净现值.生长于立地条件差的杉木人工林，其经济成熟龄及现值收益对木材市场价格、森林经营成本以及利率的变动更为敏感.

碳价格在较大范围内变化对经济成熟龄的影响并不显著，碳价格在0～800元·t-1的区间变化，经济成熟龄呈现提前1～3 a的变化特征.朱臻等[18]研究指出在当前木材价格处于高位的条件下，碳汇价格变化对于杉木最佳轮伐期并不敏感，这与本研究结果相一致.但其研究发现当碳价格上升至800元·t-1时，杉木人工林的最佳轮伐期推迟了1 a，这与本研究得出的结论相反.这主要是由于本研究计算经济成熟龄时，木材和碳汇收益采用年均净现值法计算，从而使经济成熟龄出现提前的变化趋势.朱臻等[25]对森林经营主体的杉木碳汇供给潜力进行比较研究，指出随着碳价格的提高，杉木的轮伐期开始提前.这也表明碳汇经营目标和木材经济目标是可以兼容的，林业经营者不用推迟经济成熟龄以获取更大的碳收益，朱臻等[16,18]研究也证实了这一点.此外，本研究在增加碳汇收益情况下经济成熟龄还具有提前的变化特征，进一步验证了碳汇木材复合经营目标的兼容性，有利于促进碳汇造林相关政策的推广与实施，促使林业经营者积极主动开展人工林碳汇经营.

参考文献

[1] KANT S, WANG S, DEEGEN P, et al. New frontiers of forest economics[J]. Forest Policy and Economics, 2013, 35(4):1-8.

[2] GUNALAY Y, KULA E. Optimum cutting age for timber resources with carbon sequestration[J]. Resources Policy, 2012,37(4):90-92.

[3] SAMUELSON P A. Economics of forestry in an evolving society[J]. Economic Inquiry, 1976,14(4):466-492.

[4] VAN KOOTEN G C, BINKLEY C S, DELCOURT G. Effect of carbon taxes and subsidies on optimal forest rotation age and supply of carbon services[J]. American Journal of Agricultural Economics, 1995,77(2):365-374.

[5] STAINBACK G A, ALAVALAPATI J. Economic analysis of slash pine forest carbon sequestration in the southern U.S.[J]. Journal of Forest Economics, 2002,8(2):105-117.

[6] SPRING D A, KENNEDY J O S, MAC NALLY R. Optimal management of a forested catchment providing timber and carbon sequestration benefits: climate change effects[J]. Global Environmental Change, 2005,15(3):281-292.

[8] YOSHIMOTO A, MARUSAK R. Evaluation of carbon sequestration and thinning regimes within the optimization framework for forest stand management[J]. European Journal of Forest Research, 2007,126 (2):315-329.

[9] ASANTE P, ARMSTRONG G W， ADAMOWICZ W L. Carbon sequestration and the optimal forest harvest decision: a dynamic programming approach considering biomass and dead organic matter[J]. Journal of Forest Economics, 2011,17(1):1-17.

[10] 吴承祯,洪伟.福建省杉木人工林序列林价及其应用研究[J].福建林学院学报,1995,25(3):218-222.

[11] 何宗明,林思祖,洪伟,等.不间伐栽培模式杉木人工林成熟规律研究[J].福建林学院学报,1997,17(4):309-312.

[12] 周国模,郭仁鉴,韦新良,等.浙江省杉木人工林生长模型及主伐年龄的确定[J].浙江林学院学报,2001,18(3):219-222.

[13] 陈平留,刘健,郑德祥,等.速生丰产优质杉木林经济效益分析及伐期确定[J].林业科学,2001,31(Sp1):47-51.

[14] 张惠光.杉木人工林直径分布模型[J].福建林学院学报,2004,24(4):335-339.

[15] 陈则生.杉木人工林经济成熟龄的研究[J].华东森林经理,2004,18(3):1-5.

[16] 朱臻,沈月琴,张耀启,等.碳汇经营目标下的林地期望价值变化及碳供给——基于杉木裸地造林假设研究[J].林业科学,2012,48(11):112-116.

[17] 沈月琴,王枫,张耀启,等.中国南方杉木森林碳汇供给的经济分析[J].林业科学,2013,49(9):112-116.

[18] 朱臻,沈月琴,吴伟光,等.碳汇目标下农户森林经营最优决策及碳汇供给能力——基于浙江和江西两省调查[J].生态学报,2013,33(8):2 577-2 585.

[19] 吴承祯,洪伟.杉木人工林Sloboda树高生长模型及其最优拟合研究[J].福建林学院学报,1998,18(1):12-15.

[20] 何宗明,林思祖,俞新妥,等.杉木人工林自然生长模型的研究[J].福建林学院学报,1997,17(3):231-234.

[21] 黄贤松,吴承祯,洪伟,等.杉木人工林碳收获预估技术研究[J].自然资源学报,2013,28(2):349-359.

[22] KECA L, KECA N, PANTI C D. Net present value and internal rate of return as indicators for assessment of cost-efficiency ofPoplarplantations: a Serbian case study[J]. International Forestry Review, 2012,14(2):145-156.

[23] HOLOPAINEN M, MKINEN A, RASINMKI J, et al. Uncertainty in forest net present value estimations[J]. Forests, 2010,1(3): 177-193.

[24] 李晨燕.福建柏人工林经济成熟的研究[D].福州:福建农林大学,2007.

[25] 朱臻,沈月琴,徐志刚,等.森林经营主体的碳汇供给潜力差异及影响因素研究[J].自然资源学报,2014,29(12):2 013-2 022.

(责任编辑:叶济蓉)

收稿日期：2015-05-26修回日期：2015-08-12

基金项目:福建省科技重大专项资助项目(2012NZ0001).

作者简介:巢林(1988-)，男，硕士.研究方向：数量森林经理.Email:fjchaolin@126.com.通讯作者吴承祯(1970-)，男，教授,博士生导师.研究方向：森林经营学、森林生态学.Email：fjwcz@126.com.

中图分类号:S750

文献标识码:A

文章编号:1671-5470(2016)04-0409-11

DOI:10.13323/j.cnki.j.fafu(nat.sci.).2016.04.008

Effect of combined carbon and timber management on net present value of economic maturity age inCunninghamialanceolataplantation

CHAO Lin1, LIU Yanyan2, HONG Wei1,3, WU Chengzhen1,3,4, LIN Zhuo1

(1.College of Forestry, Fujian Agriculture and Forestry University, Fuzhou, Fujian 350002, China; 2.Institute of Applied Ecology, Chinese Academy of Sciences, Shenyang, Liaoning 110016, China; 3.Key Laboratory of Fujian Forest Ecological System Process and Management, Fuzhou, Fujian 350002, China; 4.College of Ecology Resources Engineering, Wuyi University, Wuyishan, Fujian 354300, China)

Abstract:To evaluate uncertainty and risk on plantation investment, site quality, timber and carbon price, silviculture cost, impact of interest rate change on economic maturity age and present value of central area of Cunninghamia lanceolata plantation were investigated basing on sample plot surveying and previous economic indexes. Average net present value method was applied to calculate economic maturity age and present value. Results indicated that when exponential economic was 16m, interest rate P being 5% and carbon price Pc reaching 42.41 yuan·t-2, maturity age was 19 years, with average net present value max(ANPVw+c) reaching 1 695.5 yuan·hm-2. According to regression analysis, net present value NPVw+cand ANPVw+cwith forest age could be represented by Sigmoid and cubic function, respectively. Though carbon source did not influence economic maturity age, max(ANPVw+c) increased by 7.34%-9.96%. When site index increased from 8 m to 24 m exponential, economic maturity age dropped from 16 a to 25 a, with max(ANPVw+c) increasing from 225.3 to 5 680.1 yuan·hm-2. Furthermore, when max (ANPVw+c) increased by 5.65%-9.97%, timber price and silviculture cost simultaneously rose by 5%, correspondingly, max(ANPVw+c) dropped by 2.01%-4.84%, and vice versa. Economic maturity age was shortened and max(ANPVw+c) was reduced when interest rate increased. To be specific, max(ANPVw+c) dropped by 13.66%- 20.04% when interest rate increased by 1%. With Pc increasing from 0 to 800 yuan·t-1, economic maturity age was cut down by 1 to 3 years and max(ANPVw+c) increased by 2.39-2.94 times. In other word, max(ANPVw+c) increased by 11.55%-14.53% with carbon price rose per 100 yuan·t-1. To summarize, joint carbon and timber management has great impact on economic maturity age and present value. To fully play the role of plantation in carbon sequestration, integrated carbon benefit and timber resource management should be taken into emphasis.

Key words:forest management; carbon and timber manager; average net present value; present value; economic maturity age; forest carbon sequestration; Cunninghamia lanceolata