A Note on Choice Number of Some Planar Triangle-Free Graphs

ZHU Xiaoying， DUAN Ziming

(1. College of Jincheng，Nanjing University of Aeronautics and Astronautics， Nanjing 211156， China；2. Department of Mathematics， China University of Mining and Technology， Xuzhou 221008， China)



A Note on Choice Number of Some Planar Triangle-Free Graphs

ZHU Xiaoying1， DUAN Ziming2

(1.CollegeofJincheng，NanjingUniversityofAeronauticsandAstronautics，Nanjing211156，China；2.DepartmentofMathematics，ChinaUniversityofMiningandTechnology，Xuzhou221008，China)

Abstract：A graph G is k-choosable if it can be colored whenever every vertex has a list of available colors of size at least k. By using the discharging method and some structure properties of minimal counterexample graph， it is showed that every planar triangle-free graph without 6-，8- and 10-cycles is 3-choosable. The results on list coloring of planar graph is enriched.

Keywords：choosability； triangle-free graph； girth

All graphs considered here are finite， undirected and simple. LetG=(V(G)，E(G)，F(G)) be a planar graph. For a vertexv∈V(G)，d(v) andδ(G) denote its degree and the minimum degree ofG， respectively. For a facef∈F(G)，d(f) denotes the number of edges on the boundary off， where each cut edge is counted twice. We call a vertexvak-vertex ifd(v)=k， and similarly call a facefak-face ifd(f)=k. Supposekis an integer. Thenk+andk-denote integers ≥kand ≤k， respectively. A face of a plane graph is incident with all edges and vertices on its boundary. Two faces are adjacent if they have some common edges. The set of allk-cycles ofGis denoted byCk. A graph is calledCk-free ifCk=∅.

A list coloring ofGis an assignment of colors toV(G) such that each vertexvreceives a color from a prescribed listL(v) of colors and adjacent vertices receive distinct colors[1].L(G)={L(v)|v∈V(G)} is called a color list ofG. The graphGis calledk-choosable ifGadmits a list coloring for all color listLwithkcolors in each list.

Thomassen[2]proved that every plane graph is 5-choosable. Voigt[3]showed that not all planar graphs are 4-choosable. By 3-degenericity， every planar triangle-free graph is 4-choosable and Voigt[4]exhibited an example of a non-3-choosable triangle-free planar graph.

It remains to decide whether a given plane graph is 3-choosable or 4-choosable. Gutner[5]proved that these two problems are NP-hard. Sufficient conditions for 3-choosability of planar graphs are studied intensively. Thomassen[6]proved that every plane graph of girth at least 5 is 3-choosable. Lam[7]proved that every planar graph with girth at least 4 and without 5- and 6-cycle is 3-choosable. Zhang[8]proved that every planar triangle-free graph without 5-，8- and 9-cycles is 3-choosable. Dvorak[9-10]proved that every planar graph without 3-，7- and 8-cycles is 3-choosable and every planar graph without 3-，6- and 7-cycles is 3-choosable. In this paper， we show that every planar triangle-free graph without 6-，8- and 10-cycles is 3-choosable， which enrichs the results on list coloring of planar graph.

We use the following notation.

Anh-facefis called a lighth-face if all incidental vertices are 3--vertices， otherwise a non-lighth-face if it is incident with at least one 4+-vertex. Anh-face is called a minimalh-face if it is incident with exactly one 4+-vertex and 3--vertex on other vertices； similarly， anh-face is called a non-minimalh-face if it is incident with at least two 4+-vertices.

Before stating the main theorems， we shall first state the following necessary lemmas.

Lemma 1[1]Every cycle of even length is 2-choosable.

Lemma 2[8]LetGbe a non-3-choosable graph such that for any proper subsetV*⊂V，G[V*] is 3-choosable. Then any 2n-cycle ofGcontains at least one 4+-vertex.

Lemma 3[8]LetGbe a non-3-choosable graph such that for any proper subsetV*⊂V，G[V*] is 3-choosable. Then ifC1andC2are two 4-cycles with exactly one common vertexv0， then at least one ofC1andC2is a non-minimal cycle.

Our goal is to prove the following theorem.

Theorem 1IfGcontains no triangles and contains no 6-，8- and 10-cycles， thenGis 3-choosable.

ProofSuppose thatGis a counterexample of minimum order. Then it is easy to seeδ(G)≥3. By the choice ofG， we have the following claims.

Claim 1No two distinct 5-facesfandf′ are adjacent.

ProofLetf=v1v2v3v4v5andf′=v1v2u3u4u5. Asv1andv2have degree at least three， thusv3≠u3andv5≠u5. AsGdoes not contain triangles，v3≠u5andv5≠u3. Asv2v3v4v5v1u5u4u3is not an 8-cycle， {v3，v4，v5}∩{u3u4u5}≠∅. By symmetry， we may assume thatv4∈{u3，u4}. AsGdoes not contain triangles，v4≠u3， thusv4=u4. However， at least one of 4-cyclesu4u3v2v3oru4u5v1v5have one 2-vertex becauseGdoes not contain triangles. This contradicts withδ(G)≥3.

BecauseGdoes not contain triangles andδ(G)≥3， the two faces have one common edge when they are adjacent . In the same way we get the following conclusions.

Claim 2Each 4-face is adjacent to at most one 5-face and two 4-faces are not adjacent.

Claim 3Each 7-face is not adjacent to another 5-face.

(1)

The discharging rules are as follows.

(R2) From each 5-face to each adjacent 4-face calledf′ through their common edgee=uv， transfer：

(R23) 0 iff′ is a non-minimal 4-face.

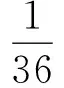
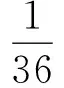
(R6) From each 9+-face to each adjacent 5-face calledf′， transfer ：

Letvbe ak-vertex ofG.

Letfbeanh-faceofG(h=4，5，7，9，11+).

Ifh=4，thenbyLemma2， fisincidentwithatleastone4+-vertex.ByClaim2， fisadjacentto5-，7-or9+-faceandfisadjacenttoatmostone5-face.Accordingtothetransferringrules，weshouldconsideradjacent5-facesand7-faceasmuchaspossible.Thisconditionisconsideredtobetheworstcase.

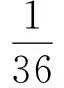
Ifh=5， fisadjacentonlyto4-and9+-facesbyClaim1andClaim3.

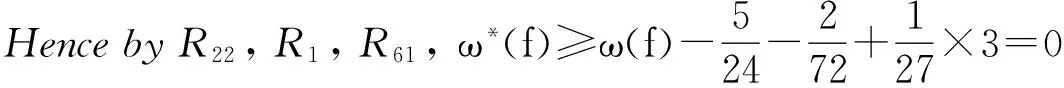
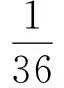
Atlast，weassumethatfisincidentwithatleastfour4+-vertices，thenumberofminimal4-facesadjacenttofandthenumberof3-verticesincidentwithfdecreased.Itisclearthatω*(f)≥0.

Assumeh≥12.Eveniftheincidentverticesareall3-verticesandthefacesadjacenttofareall4-faces，wehave

Now， we getω*(x)≥0 for allx∈V∪F. It follows that

(2)

This is a contradiction and the proof is complete.

References：

[1]ERDÖS P， RUBIN A L， TAYLOR H. Choosability in graphs [J].CongressusNumer， 1979，26： 125-157.

[2]THOMASSEN C. Every planar graph is 5-choosable [J].JournalofCombinatorialTheorySer(B)， 1994，62(1)： 180-181.

[3]VOIGT M. List colourings of planar graphs [J].DiscreteMath， 1993，120(2)： 215-219.

[4]VOIGT M. A not 3-choosable planar graphs without 3-cycles [J].DiscreteMath， 1995，146(1)： 325-328.

[5]GUTNER S. The complexity of planar graph choosability [J].DiscreteMath， 1996，159： 119-130.

[6]THOMASSEN C. 3-list-coloring planar graphs of girth 5 [J].JournalofCombinatorialTheorySer(B)， 1995，64(1)： 101-107.

[7]LAM P C B. The 3-choosability of plane graphs of girth 4 [J].DiscretMath， 2005，294(3)： 297-301.

[8]ZHANG H. On 3-choosability of plane graphs without 5-，8- and 9-cycles [J].JournalofLanzhouUniversity(NaturalSciences)， 2005，41(3)： 93-97.

[9]DVORAK Z， LIDICKY B. Planar graphs without 3-，7- and 8-cycles are 3-choosable [J].DiscreteMath， 2009，309(4)： 5899-5904.

[10]DVORAK Z， LIDICKY B. 3-choosability of triangle -free planar graphs with constraints on 4-cycles [J].SiamJournalonDiscreteMathematics， 2010，24(3)： 934-945.

Received date：2015-06-25

CLC Number：O 157.5 A

Document code：A

中图分类号：O 157.5

关于一些无三角形的平面图选择数的一个注记

朱晓颖1，段滋明2

(1. 南京航空航天大学 金城学院，南京 211156； 2. 中国矿业大学 理学院 数学系，徐州 221008)

摘要：对每一顶点给定至少为k种颜色的列表，若图G可以正常着色，称G是k-可选择的.本文利用差值转移的方法和最小反例图的结构性质，证明了每个不含三角形且无6-圈，8-圈和10-圈的平面图是3-可选择的，丰富了平面图列表染色的结果.

关键词：可选择的； 不含三角形平面图； 围长

Article ID： 0427-7104(2016)03-0284-04

Biography： ZHU Xiaoying(1979—)， female， lecture， E-mail： 10522520@qq.com.