基于HLLC近似Riemann解的自由面流动数值模拟
李泠泉,杨爱明
(复旦大学 航空航天系,上海 200433)
基于HLLC近似Riemann解的自由面流动数值模拟
李泠泉,杨爱明
(复旦大学 航空航天系,上海 200433)
摘要:对于自由面流动问题,发展了一种新的数值模拟方法.在该方法中,自由面的捕捉通过求解Level Set方程实现.该方程与流体力学控制方程耦合形成双曲系统方程,并采用人工压缩方法进行求解.为了提高计算的分辨率,发展了一种有限体积框架下的高阶WENO格式,并构造了基于HLLC近似Riemann算子的通量函数.对若干典型自由面流动问题进行了数值模拟,计算结果表明了该方法的有效性.
关键词:自由面流动; Level Set方程; WENO格式; HLLC近似Riemann算子; 人工压缩方法
很多自然科学与工程技术问题都涉及自由面流动问题,比如贴近海面飞行的飞行器与自由面相互作用的问题、船舶的水动力学问题等.含自由面的流动一般比较复杂,自由面的拓扑结构也会经常发生变化,尤其是涉及到复杂外形物体与自由面的相互作用时,这类问题会变得更加复杂.因为很难得到这类问题的解析解,所以数值模拟成为求解含自由面流动问题的重要手段,自由面流动的数值模拟也日益成为计算流体力学领域的热门研究问题.
本文采用LS(Level Set)方法对自由面流动问题进行数值分析.该方法最早由Osher等[1]提出来,后被广泛应用于各种自由面问题的数值模拟.
传统的LS方法将LS方程与流体力学方程分开求解,即在得到流场信息后再推进LS方程.这种求解方法不能实现流场与自由面的同步演化,自由面的演化过程存在一定的滞后现象[2-6].另外,广泛应用于自由面流动分析的数值方法大多只有2阶精度[2,4],在某些分辨率要求较高的问题中,2阶精度的数值方法对某些细微的流动结构捕捉不到.
基于此,本文将不可压流体力学方程与LS方程耦合求解,通过引入伪时间导数项,得到关于伪时间的双曲系统方程,并采用人工压缩方法进行求解.为了提高数值方法的分辨率,本文在有限体积框架下发展了一种基于HLLC(Harten-Lax-van Leer-Contact)近似Riemann解的高阶WENO格式.
1控制方程
在LS方法中,用一个函数Ф(x,t)的零值面来描述自由面.该方法的优点是可以精确地捕捉到自由面拓扑结构的变化.以二相流为例,假设物理区域Ω1中为流体A,Ω2中为流体B,Γ(t)为两种流体的交界面.假设t=0,用d(x,Γ(0))表示计算点x到自由面Γ(0)的距离,定义LS函数为计算点到自由面的符号距离函数:
(1)
该函数要能够在任意时间描述自由面,即需满足

(2)
即
φt+V·φ=0.
(3)
上式中,V为流体速度.
对于不可压缩流体,连续性方程为
·V=0.
(4)
在上式中引入压强关于伪时间的导数项,可以得到

(5)
其中:β为人工压缩系数;p为压强;τ为伪时间.如果压强在伪时间上收敛,那么连续性方程也成立.类似地,对于2维问题,在动量方程中引入动量关于伪时间的导数项,可以得到


(6)
上式中:g为重力加速度;P=p/β;u和v分别为速度V在x和y方向上的分量,黏性应力项为

本文中μ为分子黏性系数,暂不考虑湍流流动.
将(3)、(5)和(6)式耦合,可以得到如下的系统控制方程:

(7)
其中:
2数值方法
对任意控制体将(7)式进行积分,可以得到积分形式的控制方程:

(8)
上式中: Ω代表控制体单元,∂Ω代表其单元边界,S代表面积矢量,无黏通量H和黏性通量Hv为
H=Ei+Fj,Hv=Evi+Fvj.
其中:
i=(1,0),j=(0,1).
用Wi,j和Gi,j表示单元上的体积平均,可以得到半离散形式的控制方程:
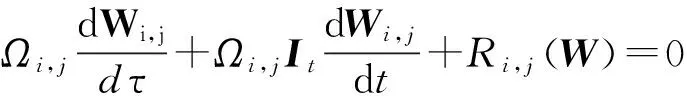
(9)
残值R的定义为

上式中,无黏通量的计算采用了高阶高斯积分,αk和Hk为高斯积分点处的权重和函数值,N为高斯点个数,本文中N=2.黏性通量的离散采用中心平均格式.
2.1HLLC近似Riemann解
下面将详述如何利用HLLC近似Riemann解来给出单元界面上的无黏通量.对一个法向为n=(nx,ny)的控制面,无黏通量为

其中q=unx+vny.该通量的Jacobian矩阵为
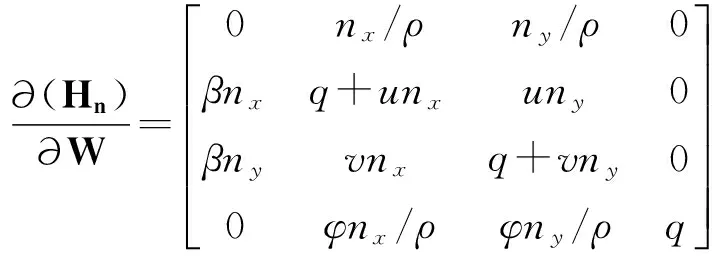
该Jacobian矩阵的特征值为
λ1=q-c,λ2=q,λ3=q,λ4=q+c,
(10)
其中

HLLC近似Riemann解是Toro等[7]在HLL近似Riemann解[8]的基础上发展出来的一种新的近似求解Riemann问题的方法.在该方法中,Riemann问题的解用图1(见第324页)所示的三波模型进行近似.相比于HLL近似Riemann解,HLLC近似Riemann解包含了接触间断,适合于模拟自由面流动问题.
下面给出方程(7)所对应的HLLC近似Riemann解.WL和WR代表单元界面左右两侧的重构守恒变量.对于接触间断有
(11)
对于左右两边的非线性波,利用Rankine-Hugoniot条件有
(12)
上式中左右波速的估计采用如下方法:

上式中,上标~代表相应物理量的Roe平均值.将(12)式展开成分量形式,并利用接触间断关系式(11),可以求出接触间断左右状态的值:
(13)
其中K=L,R.最后可以得到如下的HLLC通量:
(14)
其中

2.2高阶WENO重构
单元交界面两侧高斯点处的守恒变量WL和WR通过高阶WENO格式重构得到.重构过程是针对原始变量进行的,得到原始变量的重构值之后再转换为守恒变量值.原始变量的定义为

下面给出重构的具体过程.
如图2所示,若已知原始变量中任一分量q在单元(m,n)上的平均值

(15)
其中m=i-2,i-1,i,i+1,i+2;n=j-2,j-1,j,j+1,j+2.单元(m,n)被4个单元界面包围,这4个界面分别记为(m+1/2,n),(m-1/2,n),(m,n+1/2)和(m,n-1/2).
基于该单元平均值,首先在ξ方向上做重构得到η方向上的面平均值,在图2中用粗实线表示出单元界面(i+1/2,n):
(16)
基于面平均值,在η方向上再进行重构,得到高斯积分点处左右两侧的原始变量值,在图2中以实心圆点表示:
(17)
上述重构过程均采用5阶WENO重构,具体方法可以参考文献[9-11].
2.3双时间推进方法
时间推进采用双时间方法.首先忽略掉方程(9)中的伪时间导数项,并将物理时间导数采用二阶向后差分近似:

(18)
上式中,上标n代表物理时间站位,Wn和Wn-1为已知量,Wn+1为未知量.将Wn+1重新记为W*,并引入未知量的伪时间导数项,则有

(19)
(19)式在伪时间方向上的定常解W*即为物理时间上的时间精确解Wn+1.伪时间导数采用1阶向后差分近似:

(20)
上式中,上标m代表伪时间站位.当m→∞时,(W*)m+1→Wn+1.方程(20)的求解采用高效的隐式LU-SSOR(Lower-Upper-Symmetric Successive Overrelaxation)方法,具体过程可以参考文献[12].
3算例与分析
3.1Rayleigh-Taylor不稳定问题
本算例计算一个空气/氦气的Rayleigh-Taylor不稳定性问题,用来验证本文方法捕捉自由面形状变化的能力.计算域为0.01m×0.04m,初始时交界面为波幅为5cm的余弦波.空气与氦气的密度分别为1.225kg/m3和0.1694kg/m3,黏性系数为1.77625×10-5kg·m-1·s-1和1.941×10-5kg·m-1·s-1.初始时流体速度均为0.计算网格大小为64×256.本算例不考虑表面张力的影响.
图3(见第326页)给出了6个时间(t=0.000,0.047,0.066,0.088,0.118,0.250s)自由面的本文计算结果,并和Puckett等[13]的计算结果作了对比,虽然本文采用的网格比文献[13]中采用的网格要稀疏,但两者得到的自由面形状的发展趋势基本一致.在重力场的作用下,密度大的空气向下运动,氦气则向上运动,自由面的扰动幅度逐渐增大;在t=0.088s时,自由面的下部形成类似蘑菇云的形状;在t=0.118s时,蘑菇云形状被拉长,此时流场的重心要比初始时的重心低,重力势能被逐渐释放出来,流场的速度逐渐变大,重力势能转变为流场的动能.用本文的方法预测出在t=0.250s时空气已经达到容器的底部,自由面拓扑结构发生变化,出现了翻转和破碎.
3.2三相流中的液泡上升问题
本算例模拟一液泡在部分盛水容器中的上升过程,验证本文方法处理多相流的能力.为了方便起见,把3种模型流体介质记为水、油和空气.3种流体的密度比取为100∶50∶1,黏性系数比取为100∶50∶1.水的密度取为1.0×103kg/m3,黏性系数取为1.7921×10-3kg·m-1·s-1.雷诺数定义为

本文中取Re=200,不考虑表面张力作用.计算几何模型如图4所示,计算域大小为3L×3.5L,初始水深2.5L,空气厚度为1L,直径为D0=2R=L的圆形油泡浸没在水中,圆心到容器底部距离为1.5L.计算网格为60×70的笛卡尔网格.初始速度场为0,泡内压强均取液泡中心处流体静压强:
p(x,y)=(ρoilR+0.5ρwaterL+ρairL)g.
一个Level Set函数Ф只能标记2种流体,而本算例包含3种流体和2个交界面,需要再引入一个Level Set函数ψ.定义Ф为到水/油交界面的符号距离函数,ψ为到水/气交界面的符号距离函数,Ф和ψ的符号设定如图4所示.
图5给出了本文计算得到的自由面形状与流场,每幅图所对应的无量纲时间t分别为0.5、1.0、1.5、2.0、2.5、3.0、3.5、4.0,从图中可以看出,在浮力作用下油泡逐渐上升.在t=1.5时,油泡底部变平;在t=2.0时,油泡变为肾形;随着油泡进一步接近水/空气界面,油泡对该自由面形成扰动,可以看到水/空气界面发生明显变化.本文计算结果与Pan等[14]的计算结果相比,两者的自由面位置基本一致.虽然本文采用的网格比文献[14]采用的网格要稀疏,但是在t=3.0时间后,本文结果捕捉到了更细节的自由面结构.
4结论
本文发展了一种采用Level Set方程与流体力学控制方程相耦合的求解自由面流动的数值方法.利用人工压缩方法,将可压缩流动的计算方法引入到不可压自由面流动的数值模拟.为了提高自由面流动计算的分辨率,本文提出了一种有效的WENO -HLLC格式,构造了基于HLLC近似Riemann解的通量计算格式.对2个典型自由面流动问题进行数值模拟,计算结果与相关参考文献的计算结果吻合很好,说明了本文算法的有效性.
参考文献:
[1]OSHER S, SETHIAN J A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations [J].JournalofComputationalPhysics, 1988,79(1): 12-49.
[2]PRICE W G, CHEN Y G. A simulation of free surface waves for incompressible two-phase flows using a curvilinear level set formulation [J].InternationalJournalforNumericalMethodsinFluids, 2006,51(3): 305-330.
[3]KURIOKA S, DOWLING R. Numerical simulation of free surface flows with the level set method using an extremely high-order accuracy WENO advection scheme [J].InternationalJournalofComputationalFluidDynamics, 2009,23(3): 233-243.
[4]SUSSMAN M, SMEREKA P, OSHER S. A level set approach for computing solutions to incompressible two-phase flow [J].JournalofComputationalPhysics, 1994,114(1): 146-159.
[5]GROOSS J, HESTHAVEN J S. A level set discontinuous Galerkin method for free surface flows [J].ComputerMethodsinAppliedMechanicsandEngineering, 2006,195(25): 3406-3429.
[6]袁德奎,陶建华.用Level-Set方法求解具有自由面的流动问题 [J].力学学报,2000,32(3): 264-271.
[7]TORO E F, SPRUCE M, SPEARES W. Restoration of the contact surface in the HLL-Riemann solver [J].ShockWaves, 1994,4(1): 25-34.
[8]HARTEN A, LAX P D, LEER B. On upstream differencing and Godunov-type schemes for hyperbolic conservation laws [J].SIAMReview, 1983,25(1): 35-61.
[9]SHU C W. High order ENO and WENO schemes for computational fluid dynamics[M]//High-order methods for computational physics. Berlin, Heidelberg: Springer, 1999: 439-582.
[10]BALSARA D S, SHU C W. Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order of accuracy [J].JournalofComputationalPhysics, 2000,160(2): 405-452.
[11]TITAREV V A, TORO E F. Finite-volume WENO schemes for three-dimensional conservation laws [J].JournalofComputationalPhysics, 2004,201(1): 238-260.
[12]YANG A, CHEN S, YANG L,etal. An upwind finite volume method for incompressible inviscid free surface flows [J].Computers&Fluids, 2014,101: 170-182.
[13]PUCKETT E G, ALMGREN A S, BELL J B,etal. A high-order projection method for tracking fluid interfaces in variable density incompressible flows [J].JournalofComputationalPhysics, 1997,130(2): 269-282.
[14]PAN D, CHANG C H. The capturing of free surfaces in incompressible multi-fluid flows [J].InternationalJournalforNumericalMethodsinFluids, 2000,33(2): 203-222.
文章编号:0427-7104(2016)03-0321-08
收稿日期:2016-01-10
基金项目:国家自然科学基金(11172070)
作者简介:李泠泉(1989—),女,硕士研究生;杨爱明(1971—),男,博士,副教授,通讯联系人,E-mail: amyang@fudan.edu.cn.
中图分类号:O 359.1
文献标志码:A
Numerical Simulation of Free Surface Flow Based on HLLC Riemann Solver
LI Lingquan, YANG Aiming
(DepartmentofAeronauticsandAstronautics,FudanUniversity,Shanghai200433,China)
Abstract:A new numerical method of simulating free surface flow problems is developed. In this method, Level Set function is used to capture free surface. Hyperbolic equations are formed by coupling the Level Set function and the hydrodynamic equations. Artificial compressibility method is used to solve the equations. In order to improve the resolution of calculation, a high order WENO scheme based on finite volume method is developed. The flux function based on HLLC Riemann solver is constructed. Several classic free surface flow problems are simulated to prove that the present method is effective.
Keywords:free surface flow; Level Set; WENO scheme; HLLC Riemann solver; artificial compressibility

