结构化学中可观测物理量的确定值与平均值

陈 兰 孙宏伟赖城明（南开大学化学学院，天津300071）



·师生笔谈·

结构化学中可观测物理量的确定值与平均值

陈 兰 孙宏伟*赖城明
（南开大学化学学院，天津300071）

摘要：以类氢原子轨道的组合态为体系，分析了能量和轨道角动量具有确定值的条件。并结合实例讨论了非本征态下的位置、能量和轨道角动量平均值的计算中容易出现的若干问题。

关键词：结构化学；可观测物理量的确定值；可观测物理量的平均值

可观测物理量的确定值与平均值是结构化学中最基本的知识点之一。而考查学生对这部分内容掌握程度的最有效方法，就是分析类氢原子轨道的组合态以及势箱中粒子的薛定谔方程本征态的组合态下相关物理量的取值问题。本文结合学生在作业和考试中容易出现的错误，总结了类氢原子轨道组合态的能量和轨道角动量具有确定值的条件，并对非本征态下的位置、能量及轨道角动量平均值的计算中存在的一些问题进行了讨论。

1 可观测物理量的确定值

量子力学中用波函数Ψ描述微观体系的状态，而对应于每个可观测的物理量A都存在一个线性厄密算符。在状态Ψ下研究物理量A时，可将算符作用于Ψ，如果作用的结果恰好等于一个常数a乘以Ψ，即Ψ=aΨ，那么Ψ为的本征态，a为的本征值，而状态Ψ下的物理量A就具有确定值a［1］。

首先考虑类氢原子轨道ψp1、ψp－1、ψpx和ψpy，它们之间的关系如式（1）和式（2）所示：

接下来讨论Ψ为类氢原子轨道的组合态，即Ψ=∑ψnilimi时的能量、轨道角动量的平方和轨道角动量的z分量，将算符、和分别作用于Ψ，有：和ψp－1都是轨道角动量z分量算符的本征态，而用作用于式（1）的结果表明，ψpx和ψpy

当所有的ni相同时，由式（3）有：

当所有的li相同时，由式（4）有：

当所有的mi相同时，由式（5）有：i

2 可观测物理量的平均值

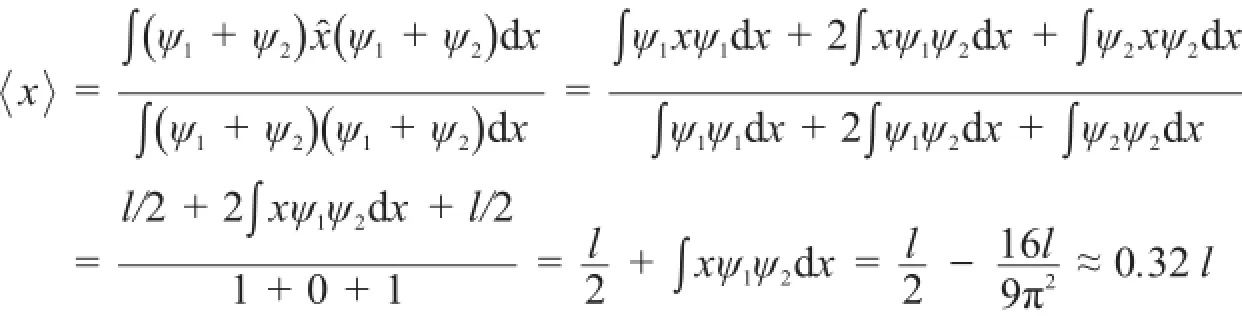
图1 一维势箱中粒子的波函数及概率密度图

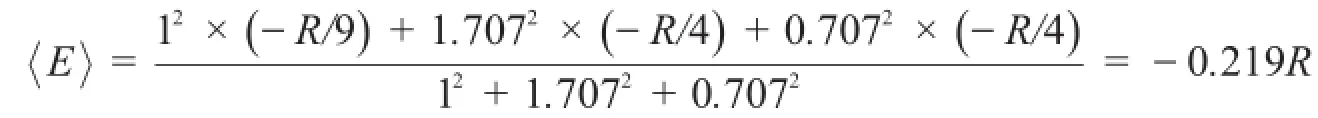
所以Ψ的Mz具有确定值0。再看角动量的平方M2，ψs、ψpz和ψdz2也都是的本征函数且相互正交，但它们的角量子数不相等，所以Ψ的M2没有确定值，其平均值（Ψ已归一化）见式（11），其角动量的均方根。

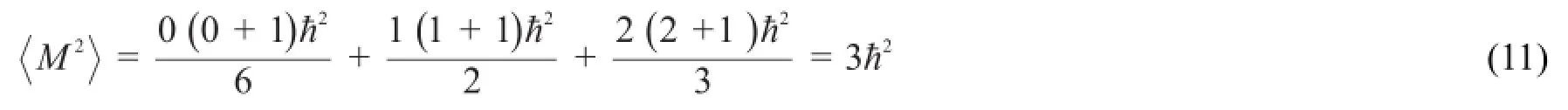
与式（11）相对应请看式（12）：

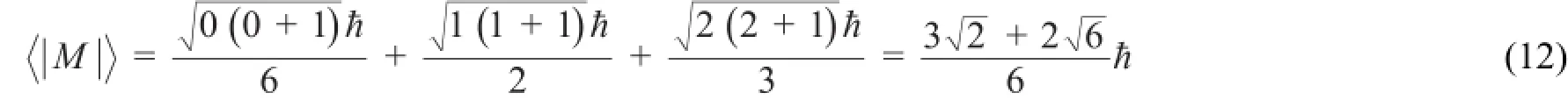
参考文献

［1］周公度，段连运.结构化学基础.第4版.北京:北京大学出版社，2008.

［2］Levine，I.N.Quantum Chemistry.6th ed.北京:世界图书出版公司，2011.

中图分类号：O641；G64

doi:10.3866/PKU.DXHX20160470www.dxhx.pku.edu.cn

*通讯作者，Email:sunhw@nankai.edu.cn

基金资助：国家基础科学人才培养基金（J1103306）

The Definite Values and Average Values of Physical Observables

CHEN Lan SUN Hong-Wei*LAI Cheng-Ming
（College of Chemistry，Nankai University，Tianjin 300071，P.R.China）

Abstract:For systems with state formed from the combination of hydrogen-like orbitals，the conditions for having definite values of physical observables such as energy and angular momentum have been analyzed.Several problems are also discussed in finding average values of position，energy and angular momentum for non-eigenstates.

Key Words:Structural chemistry；Definite values of physical observables；Average values of physical observables