三瓣波滚道圆柱滚子轴承载荷分布特性研究

卢振伟, 卢羽佳, 邓四二

(1. 洛阳LYC轴承有限公司，河南 洛阳 471003；2. 航空精密轴承国家重点实验室，河南 洛阳 471003；3. 河南科技大学 机电工程学院，河南 洛阳 471003)

轴承的载荷分布特性直接影响着轴承的使用寿命与可靠性，是评价轴承力学特性的重要指标。近年来，国内外学者对圆柱滚子轴承的载荷分布进行了大量研究。文献[1]采用静力学研究了圆柱滚子轴承的接触问题，分析了轴承的载荷分布特性，但建立的模型未考虑滚子的惯性力与润滑剂的作用，故不能准确分析高速圆柱滚子轴承的载荷分布；文献[2]采用拟静力学法建立了考虑轴承径向游隙与油膜厚度的圆柱滚子轴承分析模型，分析了轴承的载荷分布情况；文献[3]考虑套圈的柔性变形，建立了高速薄壁圆柱滚子轴承的拟静力学分析模型，分别研究了刚性套圈与柔性套圈在不同径向载荷、套圈厚度下的载荷分布；文献[4]通过高速圆柱滚子轴承的拟静力学模型，分析了滚子倾斜对轴承载荷分布的影响；文献[5]通过虚滚子假设，采用静不定方法分析了圆柱滚子轴承的游隙、滚子数量、转速及径向载荷对轴承载荷分布的影响；文献[6-7]建立了高速圆柱滚子轴承的拟动力学模型，分析了转速、游隙、载荷与滚子倾斜等因素对轴承载荷分布的影响；文献[8]建立了高速圆柱滚子轴承的动力学分析模型，分析了轴承在不同径向载荷下，滚子与套圈间的接触载荷分布情况；文献[9]建立了圆柱滚子轴承的非线性动力学模型，分析了滚道与滚子分别存在几何误差时轴承的载荷分布。

上述研究均针对普通圆柱滚子轴承，对三瓣波滚道轴承载荷分布的研究较少。且三瓣波滚道圆柱滚子轴承在外圈圆周方向有3个预载处，以增加滚道对非承载区滚子的预紧力[10]，因此载荷分布情况相对复杂。鉴于此，基于滚动轴承动力学分析理论，建立了三瓣波滚道圆柱滚子轴承的非线性动力学微分方程组，采用GSTIFF变步长积分法对其进行求解。对三瓣波滚道圆柱滚子轴承在不同结构与工况参数下的内部载荷分布情况进行分析。

1 轴承动力学分析模型

三瓣波滚道圆柱滚子轴承的结构如图1所示，外圈固定，内圈旋转，保持架由外圈引导，轴承端面喷油润滑。假设轴承零件的工作表面为理想几何形状，形心与质心重合。

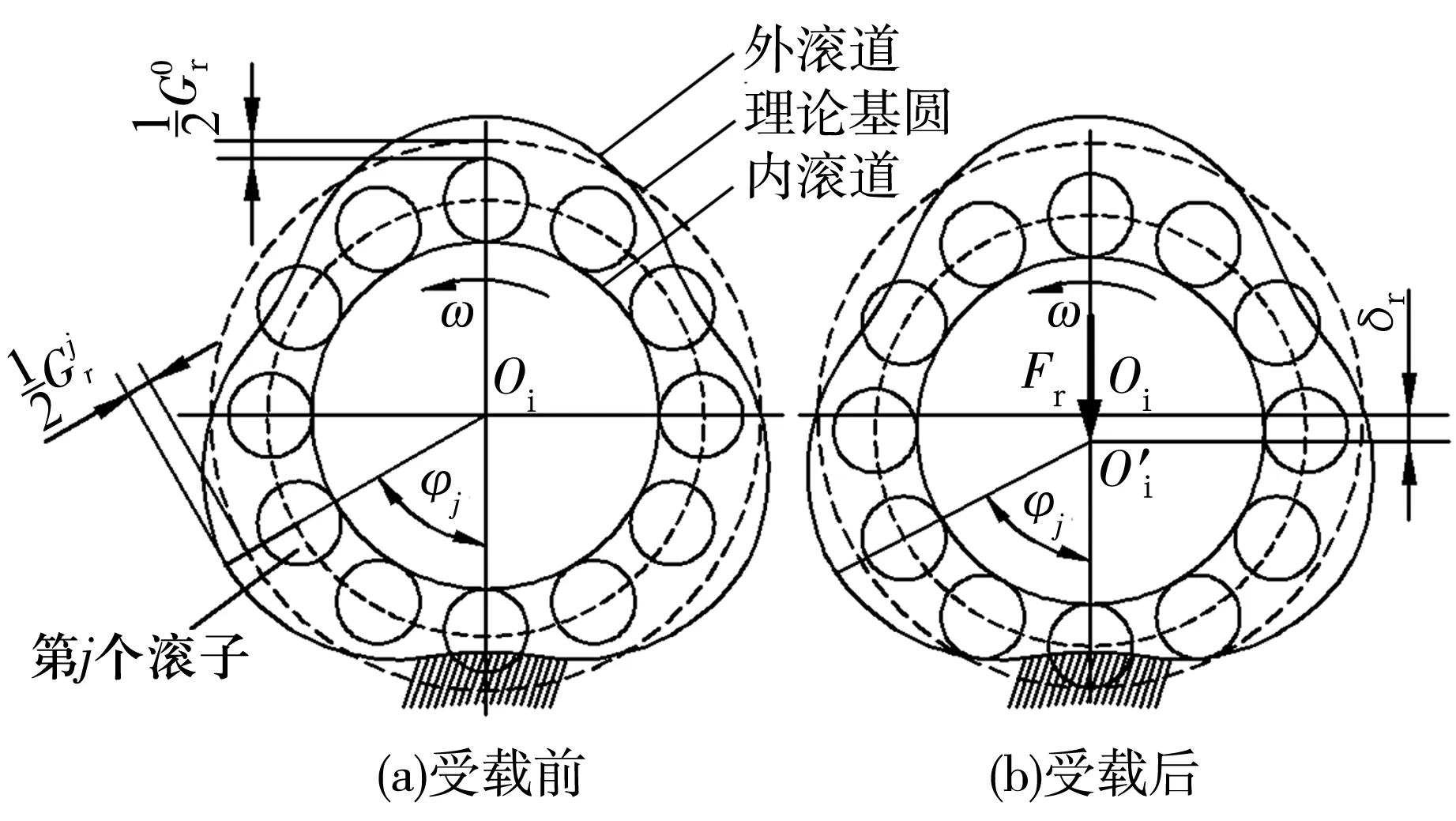
图1 三瓣波滚道轴承结构示意图

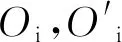
1.1 各零件间受力分析

1.1.1 滚子与滚道间作用力

三瓣波滚道圆柱滚子轴承受到径向力Fr与倾覆力矩M作用时常常会发生倾斜，滚子与内、外圈间的受力变形关系如图2所示。Oxyz为惯性坐标系，Orjxrjyrjzrj为滚子中心的坐标系，内圈倾斜角为α，位置角φj处第j个滚子倾斜角为θj，上标i,e分别代表轴承的内、外滚道(下同)。由于倾斜情况下滚子与滚道间不是理想的线接触，因此，采用切片法求解滚子与滚道间的接触问题。将滚子沿轴线方向均匀分割为N片，每片宽度为w=Lwe/N(Lwe为滚子有效长度)。

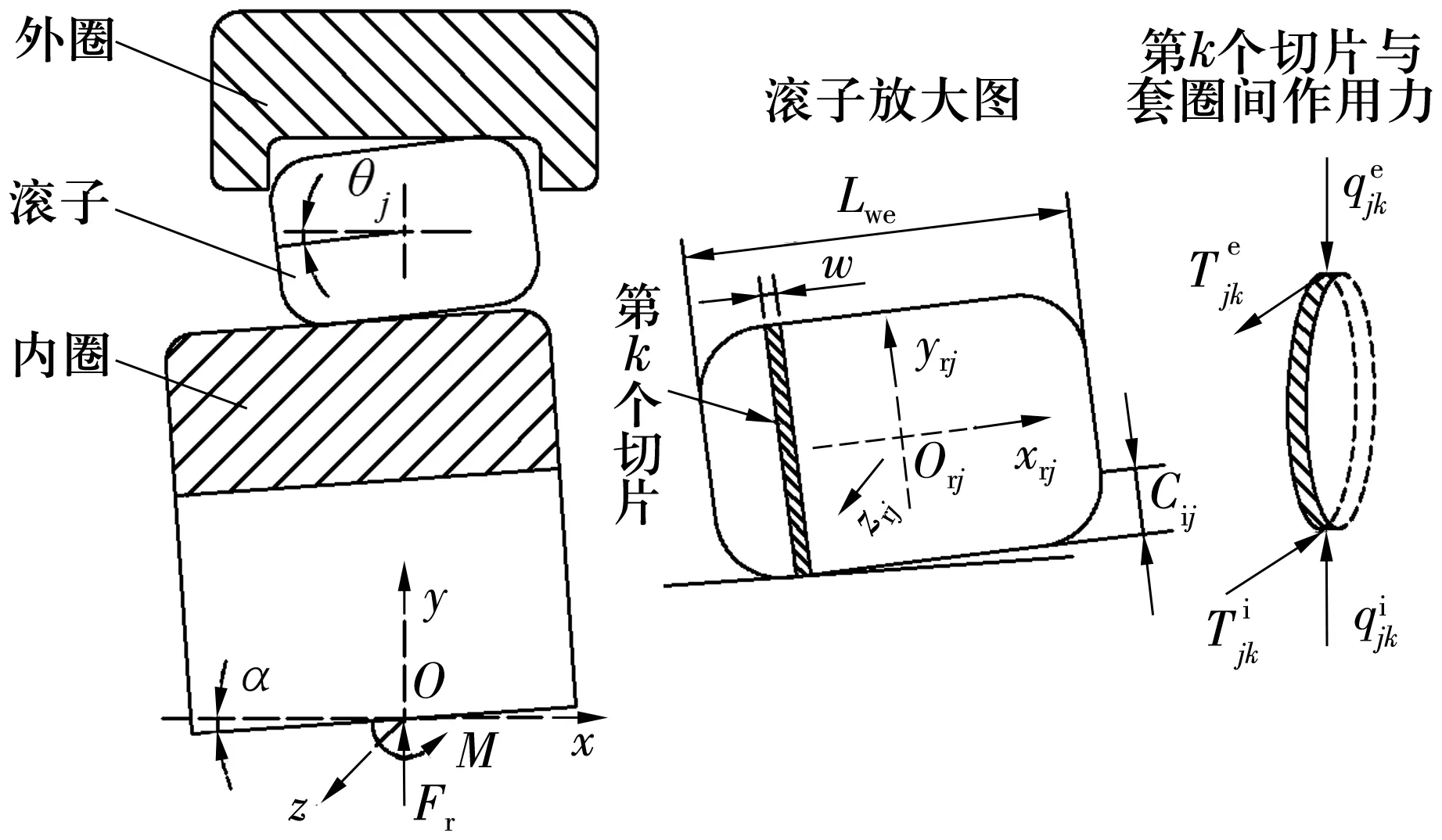
图2 滚子与套圈受力变形图

方位角φj处第j个滚子的第k个切片与内、外滚道间的弹性变形量为

(1)

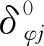
第j个滚子第k个切片与内、外滚道间的法向接触力可表示为

(2)

A=1.36η0.9，

式中：A为弹性变形量与外载荷系数；η为两接触体综合弹性常数。

第j个滚子与内、外滚道间的法向接触力为

(3)

第j个滚子由于内、外滚道与滚子间的接触力产生的附加力矩为

(4)

第j个滚子受到的油膜拖动力为

(5)

式中：μj为油膜拖动系数[11]。

第j个滚子由油膜拖动力产生的附加力矩为

(6)

1.1.2 滚子与保持架间作用力

1.1.3 保持架与引导面间作用力

套圈引导面与保持架定心表面间的相互作用由润滑剂的流体动压效应产生。由于引导挡边与保持架定心表面作用面较小且相互滑动，因此采用短颈滑动轴承理论计算保持架与引导面间作用力，作用于保持架的力Fcy，Fcz及力矩Mcx计算方法见文献[12]。

1.1.4 保持架端面及表面阻力

当轴承高速运转时，保持架的旋转使得其定心表面和端面受到周围空气/油雾混合物剪切引起的阻力作用，保持架定心表面与端面的阻滞力矩Mco计算方法见文献[12]。

1.2 轴承动力学微分方程

对于三瓣波滚道圆柱滚子轴承，滚子的受力如图3所示。

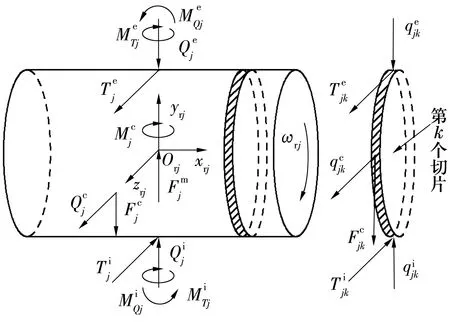
图3 滚子受力示意图

滚子所受离心力为

(7)

式中：Dpw为滚子组节圆直径；ωc为滚子的公转速度。

则第j个滚子的动力学微分方程组为

(8)

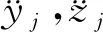
保持架的受力情况如图4所示，由图可得保持架的动力学微分方程组为

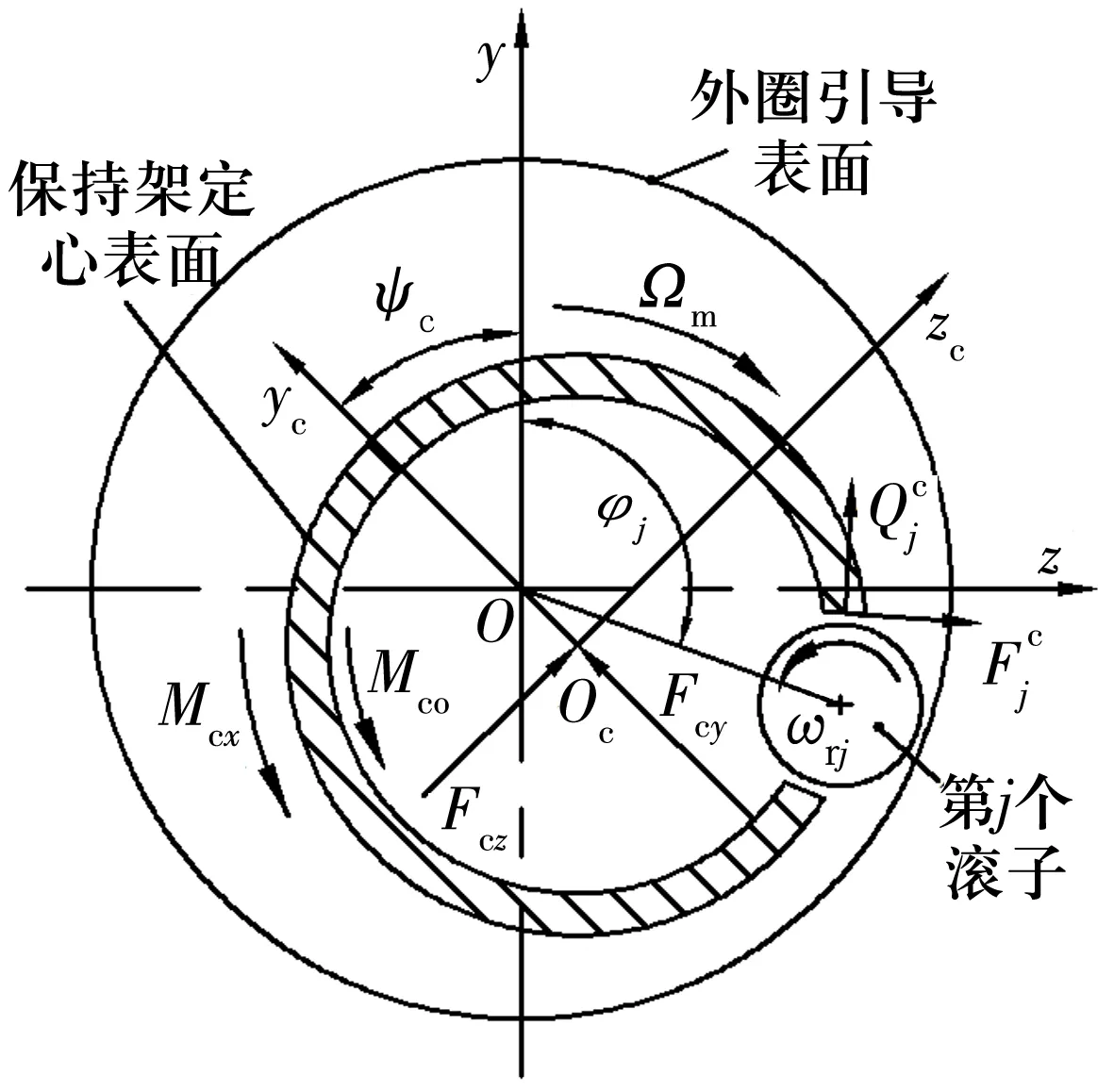
图4 保持架受力示意图

(9)

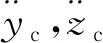
内圈的动力学微分方程组为

(10)

2 轴承载荷分布

采用GSTIFF变步长积分算法[13]对动力学微分方程组(8)～(10)进行求解，以某型号三瓣波滚道圆柱滚子轴承为例，对轴承在不同结构与工况参数下的载荷分布情况进行研究。轴承主参数见表1，内、外圈及滚子材料为8Cr4Mo4V，保持架材料为40CrNiMo。

表1 轴承主参数

2.1 三瓣波滚道结构参数对轴承载荷分布的影响

如图5所示，加工后的三瓣波滚道轮廓形状可由滚道轮廓的高、低点位置决定[14]，以滚道轮廓最低点半径Remin和滚道轮廓高低点间差值δe作为三瓣波滚道的结构参数，分析轴承在内圈转速为45 000 r/min、径向载荷为800 N、载荷方向经过滚道轮廓最低点(即采用图1中的外圈固定方式)时，结构参数对轴承载荷分布的影响。

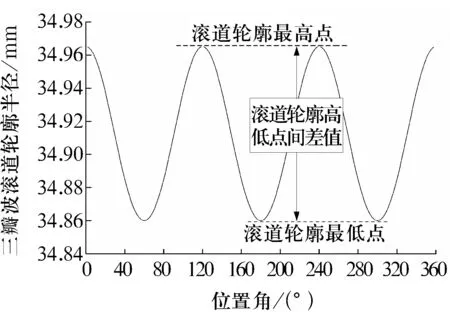
图5 三瓣波滚道轮廓形状

2.1.1 滚道轮廓最低点半径对载荷分布的影响

在滚道轮廓高低点间差值为0.06 mm时，滚道轮廓最低点半径对轴承载荷分布情况的影响如图6所示。由图6可知，三瓣波滚道轴承共有3个承载区，沿径向力方向的承载区为主承载区，滚道轮廓最低点半径增加时，由于初始游隙增大，滚子与滚道间的接触载荷、承载区面积与受载滚子个数均逐渐减小。而轴承的打滑率与疲劳寿命均会随滚子与滚道间接触力的减小而增大[6,8]，故应根据轴承的工况条件合理选取三瓣波滚道轮廓最低点半径。

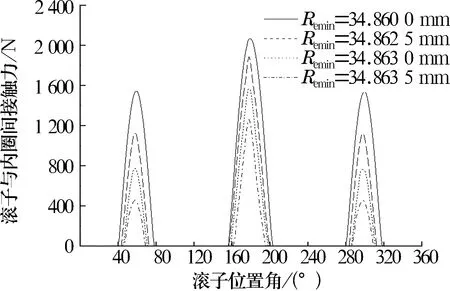
图6 滚道轮廓最低点半径对轴承载荷分布的影响

2.1.2 滚道轮廓高低点间差值对载荷分布的影响

在滚道轮廓最低点半径为34.862 5 mm时，滚道轮廓高低点间差值对轴承载荷分布情况的影响如图7所示。由图可知，随滚道轮廓高低点间差值增加，轴承最大滚动体载荷基本不变，但承载区面积与承载滚子个数逐渐减小。这是由于滚道轮廓最低点半径确定后，滚子与滚道间的最小游隙不再变化，但在其他位置角上，滚子与滚道间的游隙随滚道轮廓高低点间差值的增大而增大，使得轴承承载区面积减小。由于最大滚动体载荷基本不变，轴承的疲劳寿命变化很小，增大承载区面积可以增加承载滚子的个数，减小轴承打滑。因此，可选择较小的滚道轮廓高低点间差值。

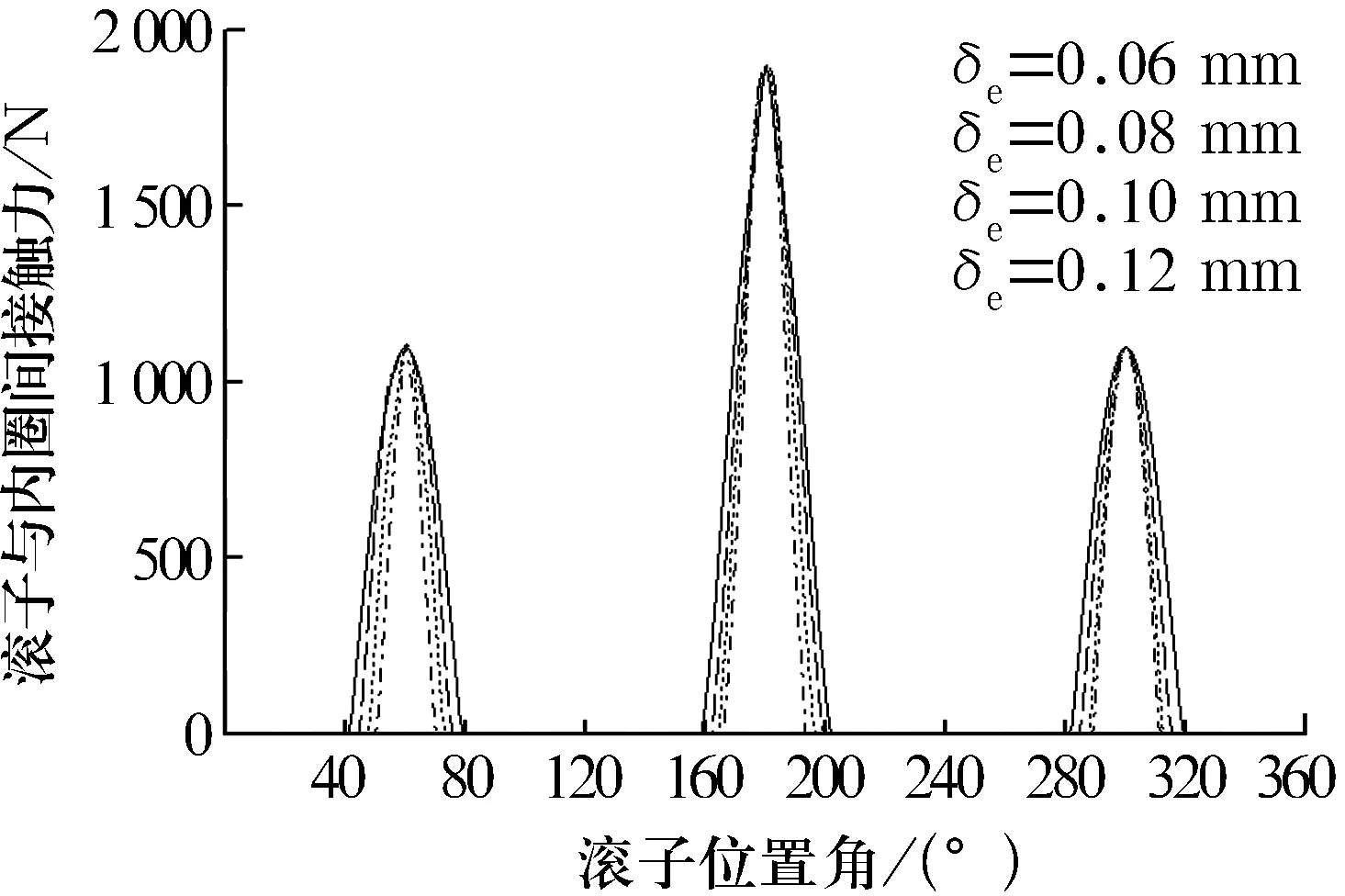
图7 滚道轮廓高低点间差值对轴承载荷分布的影响

2.1.3 滚道基圆圆度对轴承载荷分布的影响

由于加工误差的存在，采用预变形方法加工三瓣波滚道时，滚道轮廓的3个低点常常不在同一半径上[14]，此时三瓣波滚道轮廓最低点半径所在基圆的圆度不为0。在滚道轮廓最低点半径为34.862 5 mm，滚道轮廓高低点间差值为0.06 mm时，滚道轮廓基圆圆度对轴承载荷分布的影响如图8所示。由图可知，随圆度增加，在主承载区，滚子与滚道间的接触载荷增加，在两侧承载区，滚子与滚道间的接触载荷减小。这是由于随着基圆圆度的增加，滚道轮廓3个低点的半径不相等，在滚道轮廓最低点半径减小的区域，滚子与滚道间的游隙减小，滚子受到的接触载荷和承载区面积均增加，在滚道轮廓最低点半径增大的区域，滚子与滚道间的游隙增大，滚子的接触载荷和承载区面积均减小。由于滚子与滚道间的总载荷变化不大，最大滚动体载荷的增加会使轴承额定寿命减小。因此，在三瓣波滚道的加工过程中应尽量减小滚道基圆圆度，防止载荷分布不均。

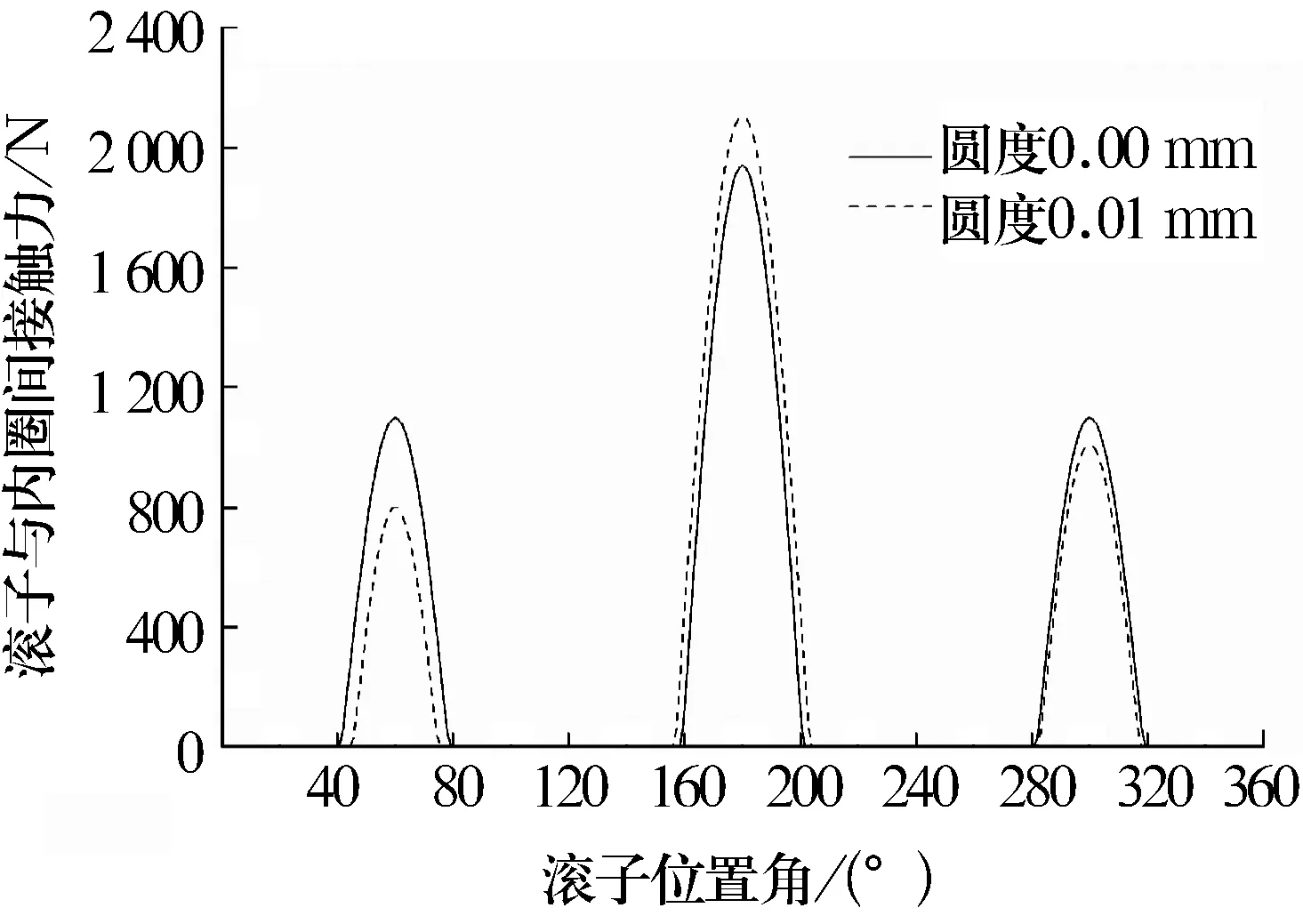
图8 滚道轮廓基圆圆度对轴承载荷分布的影响

2.2 工况参数对轴承载荷分布的影响

假设三瓣波轴承的滚道轮廓最低点半径为34.862 5 mm，滚道轮廓高低点间差值为0.06 mm，分析工况参数对轴承载荷分布的影响。

2.2.1 径向载荷对轴承载荷分布的影响

在内圈转速为45 000 r/min时，径向载荷对轴承载荷分布的影响如图9所示。由图可知，随径向载荷的增加，滚子与滚道间的接触载荷在主承载区逐渐增加，在其他承载区逐渐减小。这是由于径向载荷增加时，内圈在径向载荷方向上的位移量也增加，使滚子与滚道在3个预载区的接触载荷差值逐渐增加。

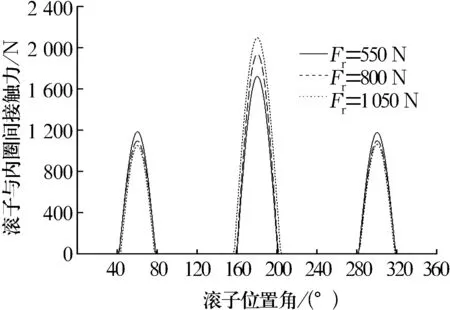
图9 径向载荷对轴承载荷分布的影响

2.2.2 外圈安装旋转角对轴承载荷分布的影响

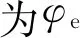
在转速45 000 r/min，径向力800 N时，外圈安装旋转角对轴承载荷分布的影响如图10所示。由图可知，随外圈安装旋转角增大，滚子与滚道间的总接触载荷基本保持不变，这是因为轴承的径向载荷与滚道结构并没有改变。但在外圈旋转角从0°变为60°的过程中，最大滚动体载荷逐渐减小，滚子与滚道间的载荷分布更加均匀。故在安装三瓣波滚道圆柱滚子轴承时应考虑使安装后的轴承承受的径向力方向经过三瓣波滚道轮廓最高点。

图10 外圈安装旋转角对轴承载荷分布的影响

3 结论

1)对于三瓣波滚道圆柱滚子轴承，滚子与滚道间的接触载荷随滚道轮廓最低点半径的增加而减小，承载区面积与承载滚子数随滚道轮廓最低点半径和滚道轮廓高低点间差值的增大而减小。

2)随着滚道轮廓最低点半径所在基圆圆度的增加，滚子与滚道间的总接触载荷基本不变，最大滚动体载荷逐渐增加。因此，在三瓣波滚道的加工过程中应尽量减小滚道基圆圆度，防止载荷分布不均，影响轴承的性能。

3)随着外圈安装旋转角的增大，滚子与滚道间的总接触载荷基本不变，最大滚动体载荷逐渐减小，滚子与滚道间的载荷分布更加均匀。在安装三瓣波滚道轴承时，应考虑使安装后的轴承承受的径向载荷方向经过三瓣波滚道轮廓最高点。