经验模态分解在滚动轴承故障诊断中的应用与扩展
张旭,李超强,杨柳,王玉良,钞仲凯
(1.洛阳轴研科技股份有限公司,河南 洛阳 471039;2.河南省高性能轴承技术重点实验室,河南 洛阳 471039;3.滚动轴承产业技术创新战略联盟,河南 洛阳 471039)
滚动轴承是旋转机械设备的关键部件,其运行状态直接影响整机的稳定性和寿命。据统计,约30%的机械故障与轴承损伤有关;其中,轴承发生剥落、点蚀等表面损伤类故障时,损伤会迅速加剧,导致轴承失效并造成整机运行受阻。因此,对轴承运行状态的监测及故障诊断至关重要。
滚动轴承故障诊断的流程如图1所示,由于信号拾取的不确定性,信号处理基本上决定了故障特征提取的正确率,是影响最终诊断结果的关键环节。目前,时频分析是主要的信号处理方法:Fourier变换是基本的时频变换,主要用于线性、稳态的频谱分析;小波分析具有多分辨率分析的特点,但选定小波基函数和变换尺度时也随之确定了分辨率大小,只能进行恒定的多分辨率分析而不具备自适应性。
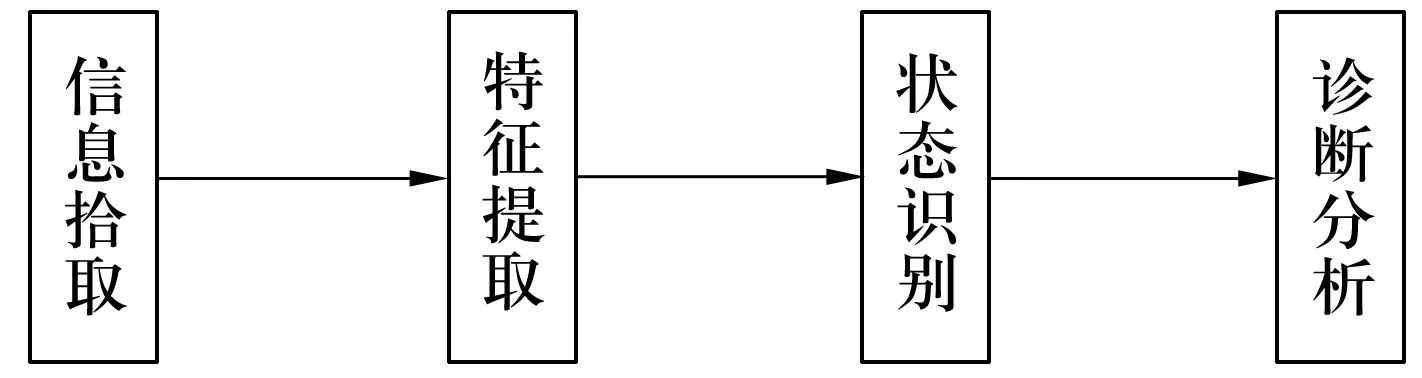
图1 滚动轴承故障诊断流程
经验模态分解(Empirical Mode Decomposition,EMD)摆脱了Fourier变换的局限性,可用于非线性、非平稳信号的分析;另外,其依据信号自身的局部特征信息进行自适应分解, 得到一系列具有不同时间特征尺度的固有模态函数( Intrinsic Mode Function,IMF) 分量,能够进行自适应的多分辨率分析;经验模态分解很好地契合了滚动轴承振动信号非线性、非平稳的特点,近年来在轴承故障诊断领域得到了广泛应用和不断扩展。
1 经验模态分解
1.1 基本原理
EMD算法的基本原理是将原始的时间信号分解为一组IMF分量和残余分量的和,即
(1)
式中:x0(t)为初始信号;Ii(t)为第i个IMF分量;rn(t)为残余分量。IMF分量必须满足2个条件:1)极值点与过零点的个数相等或最多相差1;2)任意时间段内由局部极大值点组成的上包络线与由局部极小值点组成的下包络线的均值为零。EMD算法的具体步骤为:
1)初始化定义x(t)=r0(t)=x0(t);
2)获取x(t)中的所有局部极值点;
3)使用样条函数对局部极大值、极小值点进行曲线拟合,并求取上下包络线的均值m(t);
4)定义d(t)=x(t)-m(t),并判断d(t)是否满足上述条件,如果不满足,令x(t)=d(t),重复第2)~3)步,直到d(t)满足IMF条件并记为I1(t)=d(t);
5)定义x(t)=r1(t)=r0(t)-d(t),重复以上步骤,依次得到n个IMF分量,记为I1(t),I2(t),…,In(t),在满足预定的筛选停止准则后停止,最终留下初始信号的残余分量rn(t)。
青年是国家的未来,高校和科研机构肩负培养未来具有创新能力人才的重任。“长江计划”青年学者清华大学教授崔勇指出,高质量的教学工作能激发学生的创造思维,使更多的科研课题得以被发掘、探索,从而推动科研成果产出; 而高水平的科研成果能促进学科知识更新,从而使教育工作始终立足学科前沿。教研结合要坚持人才创新能力培养的价值导向[1]。因此,通过科研活动更新进教学内容,医学人才的创新能力得以培养和提高。
1.2 特性
1.2.1 自适应性
1)基函数自动产生。EMD处理过程中无需选择基函数,可依据信号自身信息直接、自适应的生成一系列幅值、频率可变的IMF分量。
2)IMF分量多分辨率的自适应。EMD将信号分解得到了具有不同的特征时间尺度的IMF分量,各IMF分量包含了从低到高的不同频率成分,低频成分的分量频率分辨率高,高频成分的分量频率分辨率低,使信号的特征在不同的分辨率下显示出来,从而实现多分辨率分析。
3)自适应的滤波特性。EMD处理后得到的IMF具有不同的频率成分和带宽,这些频率成分和带宽随信号的变化而变化。因此,可将EMD看作一组自适应的高通滤波器,其截止频率和带宽随信号的不同而变化。
1.2.2 IMF分量的调制性
由EMD过程及IMF分量的特点可知,IMF分量的幅值及频率均可进行调制。可变的瞬时频率和瞬时幅值在很大程度上提升了信号的分解效率,使EMD能够较好地保留原信号非平稳、非线性的特征。另外,IMF还具有波内调制的特性,可将不同Fourier频率表示的同一分量的信息涵盖到一个IMF分量中,使其具有实际的物理意义。
完备性是指可通过分解得到的IMF分量和残余分量rn(t)将原信号完全重构,但存在可忽略不计的计算机精度误差。
由EMD得到的每个IMF分量在局部上都应该是相互正交的,但还没有在理论上得到严格的数学证明。通过后验方法得出,一般信号的正交性指标通常不会超过1%,短信号在极端的情况下可能达到5%,因此认为EMD得到的各IMF分量是近似正交的。
2 EMD存在的不足
固有模态函数的判据准则、EMD停止准则,以及包络线拟合影响着IMF分量的个数、振幅、线性和稳定性,以及整体算法的迭代次数和运行效率,但这几点均已得到较好的处理。真正影响EMD算法的难题是端点效应和模态混叠现象。
2.1 端点效应
在对原信号进行包络平均时,需使用样条函数对其极大值、极小值点进行曲线拟合,并求取上下包络线的均值。但在EMD过程中,信号的端点通常不是其极值点,样条插值时会产生拟合误差,分解得到的第1个IMF分量就存在较大误差,而后续IMF分量均是在前一个IMF分量基础上的筛选,误差随着分解过程不断累积,最终污染到整个数据序列,产生许多虚假的IMF分量,导致求取的包络均值误差很大,影响最终的诊断结果。
目前,针对EMD的端点效应,一般有2种改进途径:1)在信号两端找到合适的极值点,使拟合曲线能包络整段信号,比如端点补零、极值点延拓及周期延拓等端点延拓方法;2)改进拟合函数以得到更完美的拟合曲线,比如多项式拟合、AR预测以及神经网络预测等序列预测法。但上述途径仅能在一定程度上减小端点效应,均无法彻底将其消除。
2.2 模态混叠
模态混叠是指不能依据时间特征尺度有效分离不同的模态成分,使一个固有模态函数中包含不止1个模态分量,从而无法清晰的反映信号的固有特性。一旦产生模态混叠现象,后续的信号分解均会受到影响。引起模态混叠的主要原因有:1)间断事件引起极值序列和时间特征尺度的突变,需从极值差及时间特征尺度的联合平稳度进行综合处理;2)信号间相互作用引起的模态混叠,可利用Fourier变换的位移特性及解析信号的频谱特性将不满足分离条件的复合信号进行转换,使其能得到有效分离。
3 EMD算法的扩展
尽管相对Fourier变换、小波分析等传统时频分析方法,EMD在滚动轴承故障诊断中取得了重要的突破,但端点效应及模态混叠现象的存在也减缓了EMD在实际应用中的发展。因此,研究人员在EMD的基础上对其算法进行了多方面的扩展,以满足实际应用的需求。
3.1 局部均值分解
局部均值分解(Local Mean Decomposition,LMD)的本质是将初始信号从高频至低频自适应的分解为若干乘积函数( production function,PF)的线性组合,每个PF分量均是不同尺度的包络信号与调频信号的乘积,通过反余弦函数求取PF分量的瞬时频率,与故障频率进行对比从而实现故障诊断。LMD与EMD类似,均是基于极值点进行相关定义,但LMD采用滑动平均代替了样条插值,不仅避免了过包络、欠包络现象,还有效抑制了端点效应,能够更好的提取信号的特征频率。
3.2 总体平均经验模态分解
总体平均经验模态分解( Ensemble Empirical Mode Decomposition,EEMD)将原始信号与各个幅度极小的高斯白噪声信号作为一个整体进行EMD处理,利用高斯白噪声频谱均匀分布的特性中和原始信号中的间断区域,去除模态混叠现象;并根据零均值高斯白噪声的特性,利用总体平均使加入的高斯白噪声互相抵消,从而完整的保留原始信号。需要注意的是,EEMD中加入的高斯白噪声需满足以下条件:1)不能影响原信号高频成分的极值点分布;2)使低频成分的极值点间隔减小且均匀分布,以减小曲线拟合后局部均值的误差。EEMD虽然很好地解决了模态混叠现象,但由于加入的高斯白噪声信号,增加了计算时间,不太适合信号的实时处理。
3.3 经验小波变换
经验小波变换(Empirical Wavelet Transform,EWT)是在EMD的基础上,结合小波变换理论的一种自适应特征提取方法,其核心思想是根据信号的频谱特性,对信号的Fourier谱进行自适应的分割,构建一系列合适的正交小波滤波器组,提取出具有紧支撑频谱特性的调幅调频成分,进行Hilbert变换得到有明确物理意义的瞬时频率和瞬时幅值,最终获得Hilbert谱并进行后续的故障识别。由于EWT基于小波框架进行构建,相对于EMD,不仅理论依据完备,避免了端点效应和模态混叠现象,提高了信噪比及信号分离的可靠性,而且具有较高的计算速度及较强的鲁棒性。
4 结束语
EMD及在其基础上扩展的算法均是基于时频分析的信号处理方法,目的是提取出故障特征频率,因此,EMD的发展方向是与小波包等理论的结合,试验不同的构建方式,开发出更好的频谱分割能力,更快速、完整的提取故障特征频率。另外,EMD处理后的信号还需通过神经网络或支持向量机等进行分类状态识别,以完成故障分类和识别。

