天然气门站泄漏扩散模拟研究*
肖国清 肖仁杰 陈云龙 赵恒搏 冯明洋
(西南石油大学化学化工学院 成都 610500)
天然气门站泄漏扩散模拟研究*
肖国清肖仁杰陈云龙赵恒搏冯明洋
(西南石油大学化学化工学院成都 610500)
摘要城市天然气门站安全、稳定、高效的运行有利于天然气的配送。一旦门站发生事故,则可能造成人员伤亡、经济损失和严重的社会负面影响。结合相关的经验公式,建立了适用于城市天然气门站燃气泄漏的带压降模型,又在此基础上运用FLUENT建立带压降泄漏下的扩散模型,用于门站天然气泄漏扩散的特点和影响范围分析。并且运用该模型对某城市天然气门站进行实例应用,其结果对提高城市天然气门站的安全性有着指导作用。
关键词天然气带压降泄漏模型扩散模型FLUENT
0引言
城市天然气门站又称作配气站,是天然气输气干线和城市天然气配气管网的枢纽。随着城镇化的加速,已有不少门站从以前的郊区变成了工业区,甚至人口密集的市区。再加上长年运行,门站的安全隐患有所暴露。门站的主要事故是天然气泄漏和燃烧爆炸,并且燃烧爆炸多属于泄漏的后续事件,因此需要对天然气泄漏进行泄漏扩散模拟,分析其特征。
我国对门站天然气泄漏扩散过程研究不够深入,照搬长输管道天然气泄漏的模型,与门站天然气泄漏扩散实际情况不相符。尤其是泄漏方面大多采用定常处理,不符合门站中天然气泄漏速率随着泄漏持续进行而减慢的特点。为使模拟与现实贴合,提高计算模拟的真实可靠性,笔者在前人基础上进行改进,建立管线带压降泄漏模拟的计算模型,并在带压降的泄漏模型上建立扩散模型。
1天然气泄漏模拟
1.1经验公式
当泄漏气体的流动状态为音速流动时,满足公式:
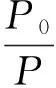
(1)
当泄漏气体的流动状态为亚音速泄漏时,满足公式:
(2)
式中,P0为泄漏点附近的环境压力,Pa;P为气体的泄漏压力,Pa;k为泄漏气体的比热容比,即气体定压比热Cp与气体定容比热Cv之比。
当泄漏气体的流动状态为音速流动时,其泄漏速率由下式计算:
(3)
当泄漏气体的流动状态为亚音速流动时,其泄漏速率由下式计算:
(4)
式中,Q为气体泄漏的质量流量,kg/s;c为气体泄放系数,其值根据泄漏孔口的形状来取值,圆形可取1.00,三角形可取0.95,长方形可取0.90;M为泄漏气体的摩尔质量,g/mol;Z为气体压缩因子,当泄漏气体为亚音速流动时,Z值可按下式计算:
(5)
当泄漏气体的流动状态为音速流动时,Z=1。
式中,ρ为气体密度,kg/m3;R为气体常数,8.314J/(mol·K);T为气体泄漏时的温度,K。
1.2泄漏模型
上述公式针对定常泄漏的工况精确度较高。由于门站内进出站的管线中都有紧急切断阀,且站内调压前后都有切断措施,一旦发生天然气泄漏,天然气的泄漏速率会随着管线内外压差的减小而降低。为简化复杂的泄漏情况,假设:①泄漏过程中,天然气温度保持不变;②紧急切断阀立即响应;③泄漏天然气满足理想气体状态方程;④很短的时间步长内,气体泄漏速率的经验公式适用。
模型的计算流程如图1所示。

图1 天然气泄漏模型计算流程
流程中涉及的其他计算公式有:
Q(k+1)=Q(k)-ΔQ(k)×Δt
(6)
(7)
式中,n(k)为天然气的物质的量,mol。
1.3实例应用
某天然气城市门站,天然气的压力分两种情况进行调压,一种是将来气的1.6MPa调整到0.8MPa进入次高压管网,另一种是将来气从1.6MPa调整到0.4MPa进入站内用气管网。其中,运输压力为1.6MPa的管道长度约为55m,0.8MPa的管道长度约为50m,0.4MPa的管道长度约为45m。各种压力下管道的输送温度均为310K,采用天然气运输管道为Φ329.1mm×7.1mm,大气压力为101.325kPa。该门站天然气组分如下表1。

表1 某门站中天然气组分 %
该门站天然气的分子量为17.450 g/mol。泄漏的压力采用1.6、0.8、0.4 MPa 3种压力,首先判定3种压力下泄漏时天然气的状态,均符合式(1)。故天然气在这3种压力下发生泄漏的流动状态均为音速流动,且当泄漏压力小于110 649.125 Pa时,天然气的泄漏状态变为亚音速流动。由式(3)~式(5)得不同工况下的天然气的初始泄漏速率如表2所示。
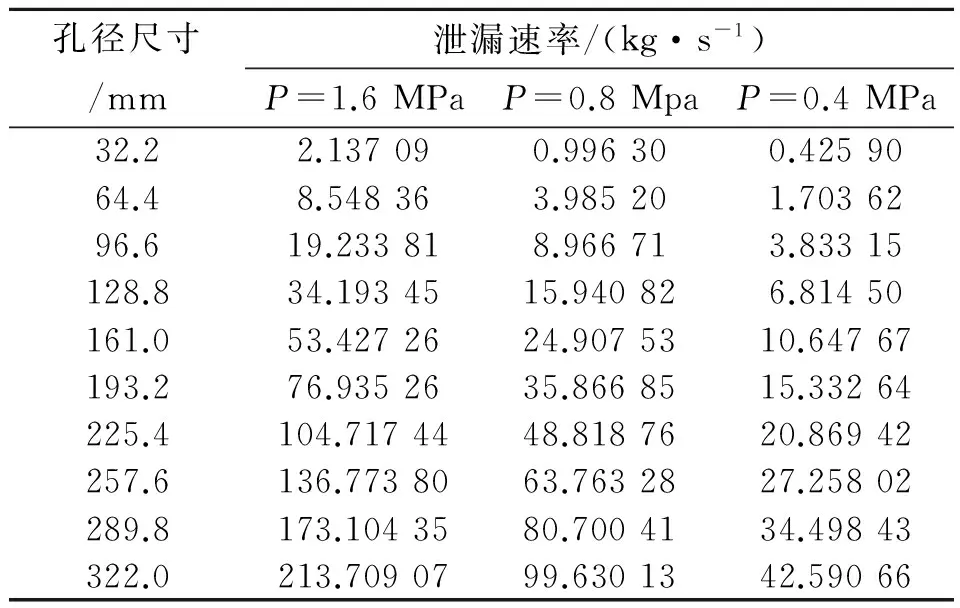
表2 不同工况下天然气的初始泄漏速率
从表2中可以看出,在相同泄漏压力下,天然气的泄漏速率随着孔径的增大而增大;在相同泄漏孔径下,天然气的泄漏速率随着压力增大而增大。同时,大孔径下天然气的泄漏速率受压力的影响比小孔径下的泄漏更大。
用模型求出孔径为32.2 mm、64.4 mm、128.8 mm、161.0 mm、管线整个断裂时的泄漏速率,泄漏速率变化曲线如下图2~图6所示。
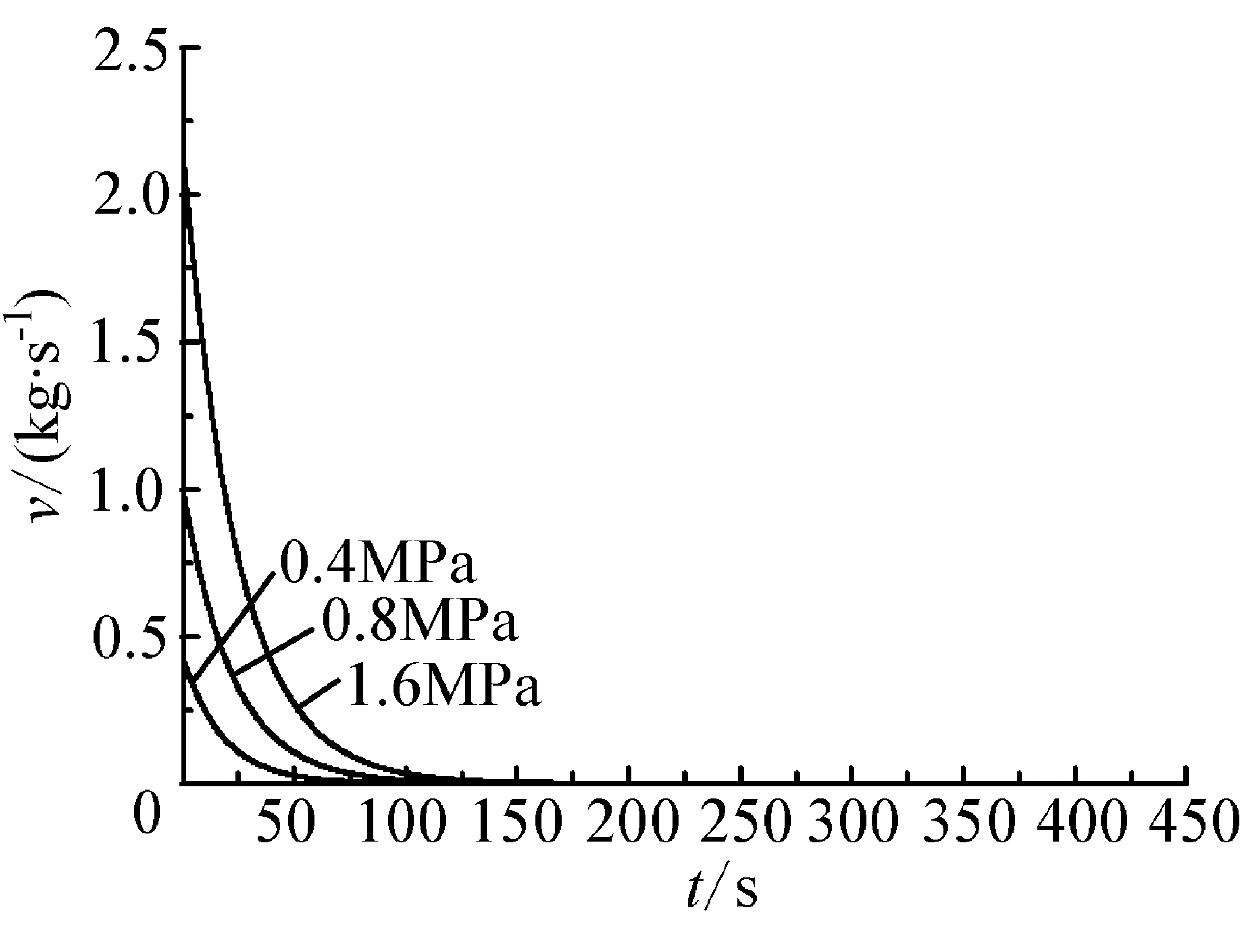
图2孔径为32.2 mm时各压力泄漏的v-t图
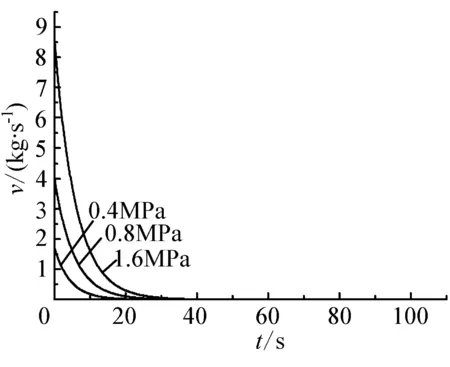
图3孔径为64.4 mm时各压力泄漏的v-t图

图4孔径为128.8 mm时各压力泄漏的v-t图
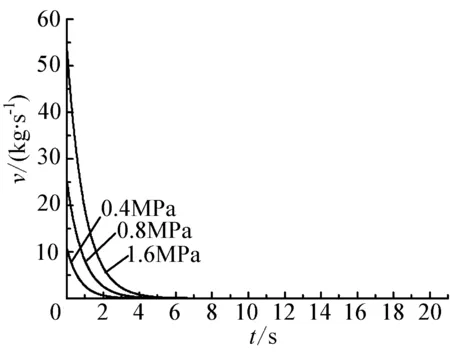
图5孔径为161.0mm时各压力泄漏的v-t图
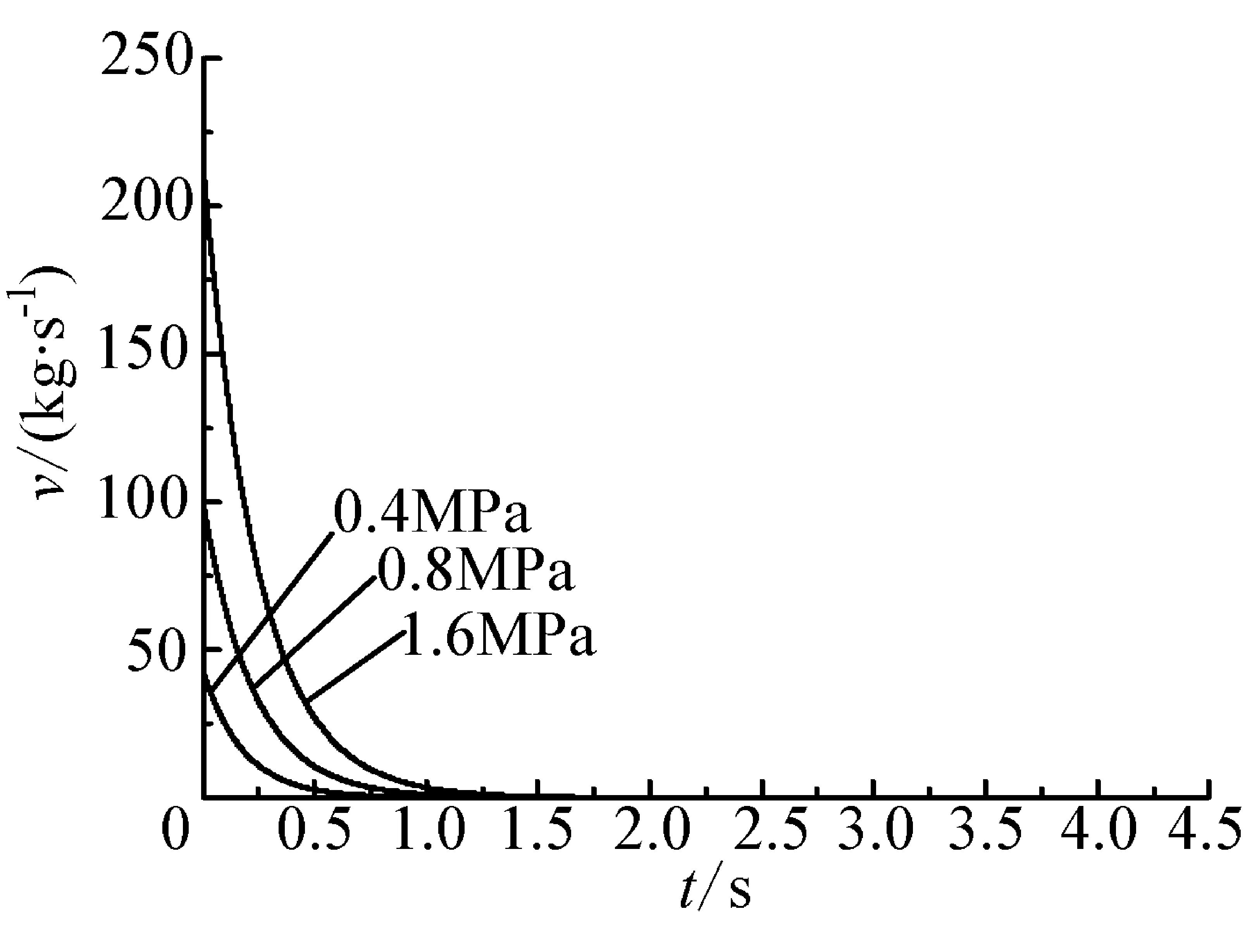
图6全断时各压力泄漏的v-t图
通过数值拟合,得FLUENT所需公式,各压力下泄漏速率随时间变化的方程分别为:
孔径为32.2 mm:
1.6 MPa----v=2.128e-0.04t;
0.8 MPa----v=0.991e-0.04t;
0.4 MPa----v=0.423e-0.05t;
孔径为64.4 mm:
1.6 MPa----v=8.406e-0.16t;
0.8 MPa----v=3.913e-0.18t;
0.4 MPa----v=1.665e-0.22t;
孔径为128.8 mm:
1.6 MPa----v=33.96e-0.66t;
0.8 MPa----v=15.82e-0.72t;
0.4 MPa----v=6.754e-0.89t;
孔径为161.0 mm:
1.6 MPa----v=52.87e-1.04t;
0.8 MPa----v=24.62e-1.13t;
0.4 MPa----v=10.50e-1.39t;
管线断裂时:
1.6 MPa----v=212.8e-4.15t;
0.8 MPa----v=99.18e-4.51t;
0.4 MPa----v=42.35e-5.55t。
由以上不同泄漏工况的v-t图可知:
(1)发生泄漏时,泄漏速率在短时间内迅速下降,且大孔径泄漏速率下降的速度比小孔径更为明显。
(2)泄漏的持续时间较短:32.2 mm孔径的泄漏在2 min内停止,64.4 mm孔径的泄漏在50 s内停止,128.8 mm的泄漏在10 s左右停止,161.0 mm的泄漏在8s内停止,管线整个断裂引发泄漏在2 s内停止。
2天然气扩散模拟
2.1物理模型及网格划分
门站中,平面布局较空旷,故针对天然气泄漏后的扩散采用二维建模。在泄漏孔径为64.4 mm的情况下,分别就网格数为3万、6万、8万、10万、20万、30万、50万进行了模拟试算,选取点(X=75,Y=20)在t=30 s时刻天然气的体积百分数为判定标准,试算结果如图7所示。
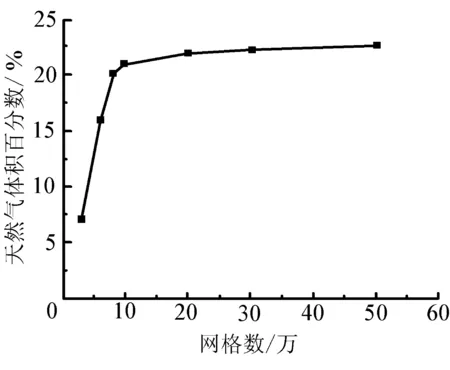
图7 网格无关性分析
从图7可以看出,网格数达到10万之后,试算结果相对稳定。考虑计算精度和资源,选取10万网格进行模拟计算。在风速入口、孔口附近,近地面需进行网格加密,所建立的网格模型如图8所示。

图8 泄漏孔径为64.4 mm条件下的建模
2.2扩散模拟
根据前文中天然气泄漏的结果,选取以下3种工况下发生天然气泄漏后的扩散进行模拟,如下表3。

表3 天然气扩散的模拟工况
(1)孔径为64.4 mm,在压力1.6 MPa下泄漏后的扩散模拟,结果如下图9~图13。

图9 t=0.625 s时扩散云图
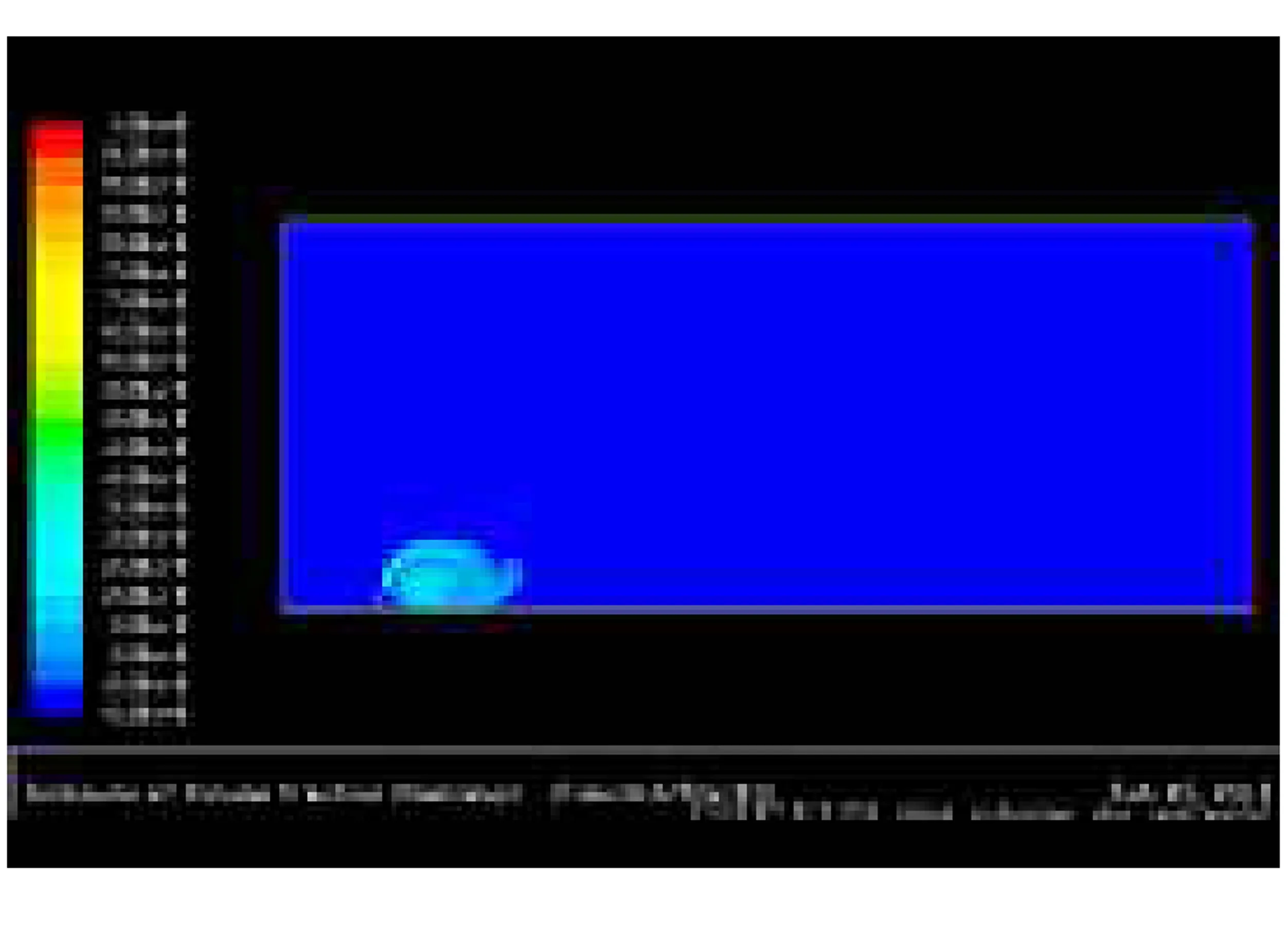
图10 t=9.025 s时扩散云图
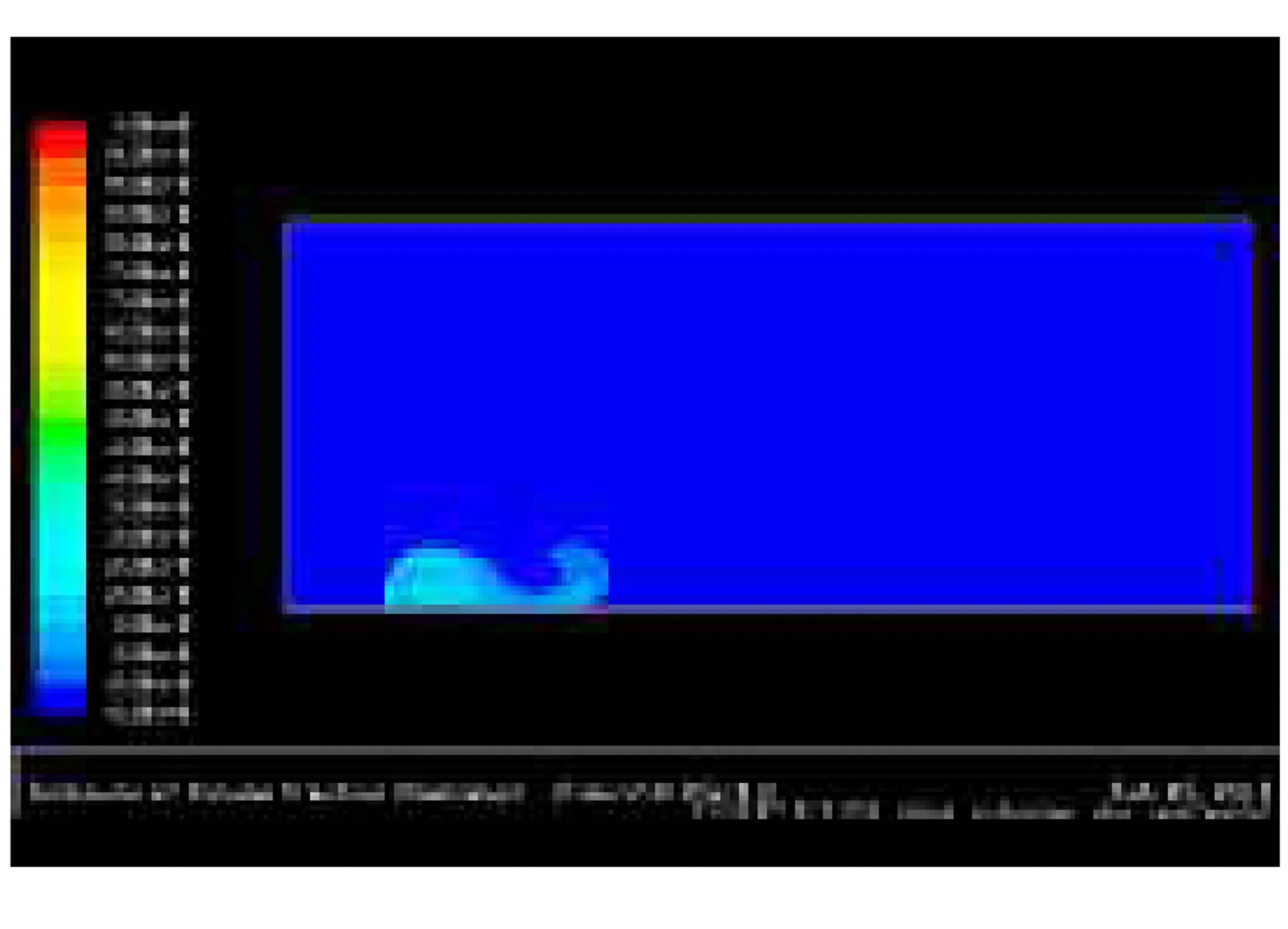
图11 t=20.125 s时扩散云图

图12 t=30.000 s时扩散云图

图13 t=30.000 s时处于爆炸极限内的扩散云图
天然气在泄漏刚发生时,压差很大,射流速度非常快。当t=3.625 s时,在重力作用下开始向近地面聚集。当t=9.025 s时,在近地面已经形成聚集区。当t=20.125 s时,泄漏速度持续减小,射流高度较初始明显降低。当t=30.000 s时,泄漏速度已经非常小,射流现象已经非常弱。
此后,聚集区会形成新的扩散前锋,但此时聚集区所存天然气较泄漏初期已很少,其扩散距离不会超过t=30.000 s时达到的距离。天然气的爆炸极限为5%~15%,此时处于爆炸极限内的云图如图13所示。
故泄漏孔径为64.4 mm,泄漏初始压力为1.6 MPa下发生天然气泄漏后在3 m/s风速下扩散,在垂直方向上影响的范围为43 m,水平方向上的影响范围为157 m,方向为下风向。
(2)孔径为128.8 mm,在压力1.6 MPa下泄漏后的扩散模拟,结果如下图14~图17所示。
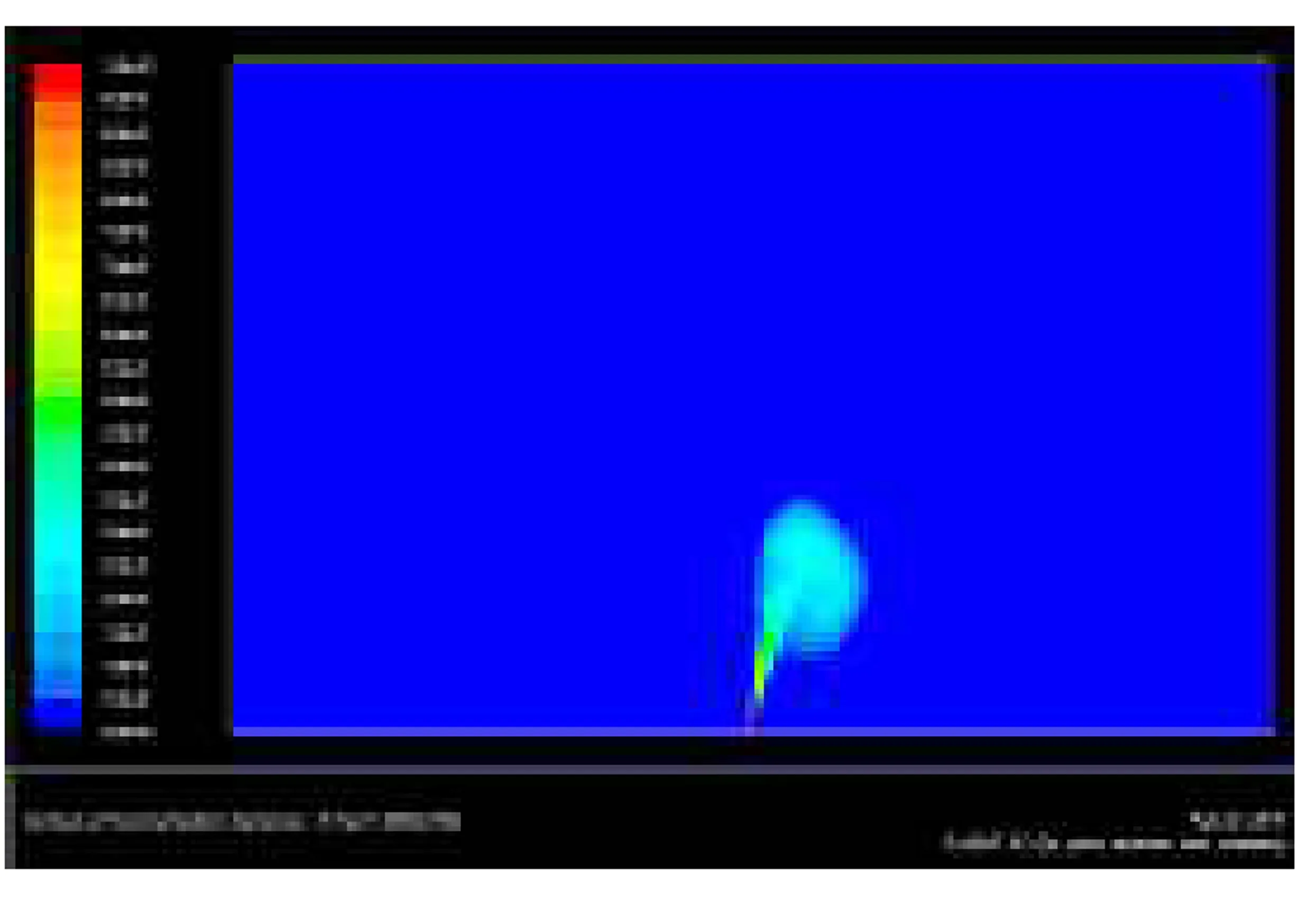
图14 t=1.000 s时扩散云图

图15 t=8.000 s时扩散云图

图16 t=17.000 s时扩散云图

图17 t=17.000 s时爆炸极限内的扩散云图
当t=1.000 s时,泄漏速度很快,由于泄漏孔径达到了128.8 mm,单位时间内泄漏出的天然气较多,射流曲线顶端的天然气浓度较高。当t=8.000 s时,单位时间泄漏出的天然气已非常少,射流已停止。当t=17.000 s时,这两部分气团是由上一个时刻的一个气团分裂而成,且浓度越来越低。根据该部分天然气的扩散轨迹可以判定,天然气的扩散已经快结束,且影响范围不会继续扩大。此时处于天然气爆炸极限内的云图如图17所示。
故泄漏孔径为128.8 mm,泄漏初始压力为1.6 MPa下发生天然气泄漏后在3 m/s风速下扩散,在垂直方向上影响的范围为54 m,水平方向上的影响范围为132 m。
(3)孔径为161.0 mm,在压力1.6 MPa下泄漏后的扩散模拟,结果如下图18~图21所示。
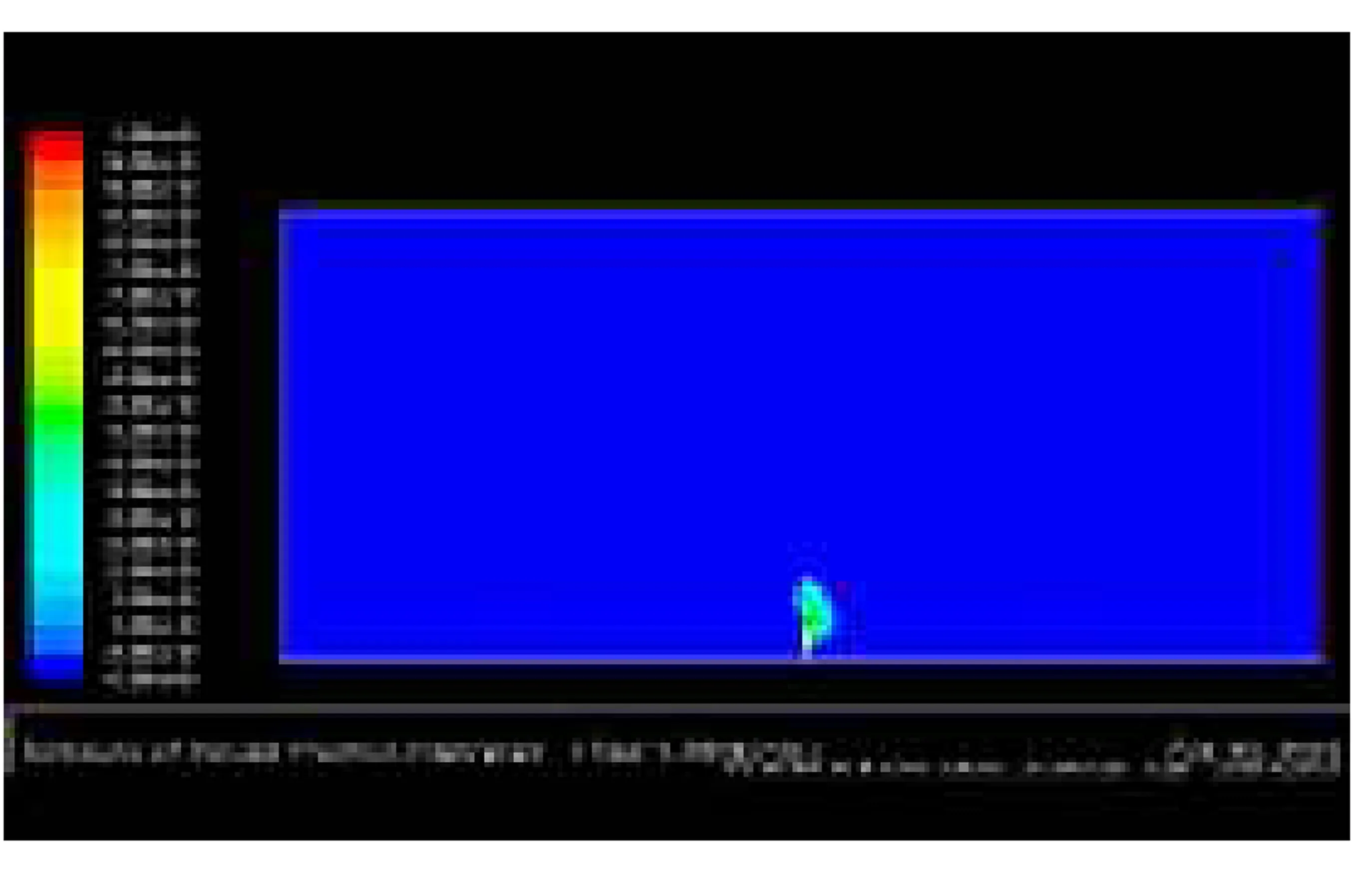
图18 t=0.195 s时扩散云图

图19 t=5.415 s时扩散云图

图20 t=10.000 s时扩散云图
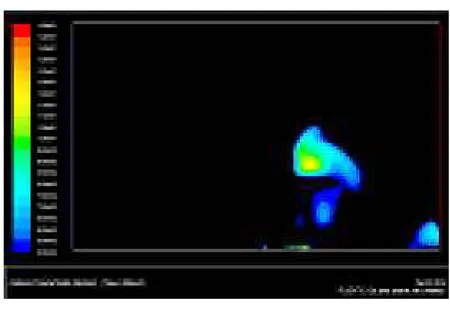
图21 t=10.000 s时爆炸极限内的扩散云图
泄漏孔径为161.0 mm,在压力1.6 MPa下的泄漏速度非常快,泄漏初期垂直方向上的射流动量远大于水平方向上风速产生的动量。当t=5.415 s时,单位时间泄漏出的天然气已非常小,故射流曲线出现断裂的趋势。当t=10.000 s时,泄漏已经停止,由于此时各个天然气团的大小已明显降低,且扩散在竖直高度上早已达到稳定,因此可以就此时刻的模拟结果得到天然气的扩散影响范围。此时处于爆炸极限范围内的天然气扩散云图如图21所示。
故泄漏孔径为161.0 mm,泄漏初始压力为1.6 MPa下发生天然气泄漏后在3 m/s风速下扩散,在垂直方向上影响的范围为57 m,水平方向上的影响范围为129 m。
3结论
(1) 以64.4、128.8、161.0 mm的孔径发生泄漏后在常年平均风速下进行扩散,在下风向的影响范围分别为157、132、129 m,在垂直方向上的影响高度分别为:43、54、57 m。
(2) 在常年平均风速下,小孔径泄漏在水平方向上的扩散距离比大孔径泄漏的扩散距离稍远;小孔径泄漏在垂直方向的影响范围比大孔径泄漏在垂直方向上的影响范围较低。
(3) 由于门站天然气存气较少,小孔径比大孔径扩散的影响范围大,说明该风速能够对该门站泄漏的天然气的稀释作用较强。
*基金项目:国家自然科学基金(51474187、51174089)。
作者简介肖国清,博士,教授,西南石油大学科研处副处长,澳大利亚皇家墨尔本理工大学国家公派访问学者,主要从事建筑物火灾控制理论、油气安全的研究工作。
(收稿日期:2015-06-10)
The Simulation Research on the Leakage and Diffusion of Natural Gas Gate Station
XIAO GuoqingXIAO RenjieCHEN YunlongZHAO HengboFENG Mingyang
(CollegeofChemistryandChemicalEngineering,SouthwestPetroleumUniversityChengdu610500)
AbstractIt is good for the distribution of gas that the natural gas gate station is in safe, stable and efficient operation. Once an accident occurs, it may cause casualties, economic losses and extremely negative social effects. Combined with the experience formula, a model with a pressure drop for gas leakage of natural gas gate station has been built. On the basis of this model, the diffusion model with pressure leaking is established by FLUENT to analyze the characteristics and the influence scope of the leakage and diffusion in natural gas gate station. As a result, it is applied in one city natural gas gate station and it proves to be directive to improve the safety of the city natural gas gate station.
Key Wordsnatural gasmodel with pressure drop for gas leakagediffusion modelFLUENT

