非本征光纤法珀传感器的振动特性研究

郭少朋， 方光荣， 刘俊标， 鞠　昱

(1.中国科学院 电工研究所，北京　100190； 2.中国科学院大学，北京　100049)



非本征光纤法珀传感器的振动特性研究

郭少朋1,2， 方光荣1,2， 刘俊标1,2， 鞠昱1

(1.中国科学院 电工研究所，北京100190； 2.中国科学院大学，北京100049)

摘要：针对光纤法珀(Fabry-Perot, FP)超声波传感器振动特性，将传感器薄板振动简化为具有集中参数的二阶振动，推导二阶振动方程的集中参数(力阻抗、等效质量、弹性系数、集中力)，获得传感器共振频率、振幅灵敏度与结构参数设计关系。测试直径2.52 mm、厚度150 μm玻璃振动薄板在空气、水中的共振频率分别为205 kHz及115 kHz，水介质中共振频率振幅灵敏度约18 pm/Pa。制作的传感器可测试局放产生超声波的最小声压约1 Pa。

关键词：局部放电；超声波传感器；集中参数；力阻抗；共振频率；频率响应

光纤法珀(Fabry-Perot, FP)传感器不仅有一般光纤传感器绝缘、耐腐蚀、抗电磁干扰等优点，亦有易制作、成本低、稳定性高等特点，在温度、压力、智能结构应变、振动、声波等测量中广泛应用[1-4]。油浸变压器内局部放电会对绝缘介质造成破坏，通过局部放电产生的超声波可定位放电源位置，修复绝缘缺陷，避免酿成重大电力事故。虽已有对该类用途传感器结构、振动膜自由频率及静压力下挠度的研究[5-10]，但针对共振频率、振幅灵敏度等关键参数研究尚少。传感器整体性能取决于振动膜的振动特性及光学参数，而传感器振动特性为传感器整体性能的基础。

本文研究油介质中传感器振动膜(或板)的振动特性时采用集中参数的二阶振动数学模型，以振动板中心速度对振动质量、力阻抗进行等效，获得振动板共振频率、振幅灵敏度与结构参数的关系，通过对计算结果实验测试，制作高灵敏度的FP传感器。研究结果对该类传类感器设计具有参考意义。

1理论分析

1.1传感器基本原理

图1的测试系统由激光器、光环形器、FP传感器、光电探测器、信号调理电路组成。激光器输出的光经环形器输入FP传感器，在FP腔内R1、R2间形成多光束干涉，干涉的反射光沿入射光纤返回，再经环形器输入光电探测器。FP传感器由含光纤的陶瓷芯体A、圆形套筒B及振动薄板C组成，一对干涉面中1个为A的光纤末端面R1，另个为C的内反射面R2，二者间距为腔长L。薄板反射面R2可随油介质中局放产生的超声波振动。工作时传感器干涉点Q设在干涉条纹中部线性区域。声波对R2的作用形成对腔长L及干涉相位的调制，传感器输出随声波振动的光强度变化信号。该信号经光电探测器及信号调理电路后输出电压信号。传感器对声波测量经声振动、光干涉、光电信号处理3环节。在超声波作用下传感器薄板的振动特性为研究传感器灵敏度的基础，该特性可用圆形固支板振动理论分析。

图1　光纤法珀传感器测量原理Fig.1 Principle of fiber FP sensor

局部放电产生的超声波范围为50～300 kHz,变压器内高频噪声(磁致伸缩噪声)低于65 kHz，超声探测常选70～180 kHz范围[11-12]。IEEE标准[13]规定厂内环境中，可以60 kHz为中心频率，现场测试时因噪声干扰可用以150 kHz为中心频率。因低频利于提高灵敏度，高频利于降低噪声，因此本文将传感器中心频率定为100 kHz。在液体介质中的传感器振动板受声波驱动力、液体对振动板的阻抗力及振动板本身的阻抗力；对小振幅板，空腔内气体对振动板的作用力可忽略。当振动板基频共振频率为100 kHz时，板振动的高次固有频率超出被测声波范围可不考虑。在仅考虑振动板基频及板中心振动时可将振动板简化为具有集中参数的二阶振动方程，即

(1)

式中：η为振动板中心位移；ω为振动角速度；t为时间；Ke为等效弹性系数；Fe为超声波作用力的等效集中力；Me，Re为考虑液体介质的等效集中质量及阻力。

获得集中参数后即可通过二阶振动方程，求解板的共振频率及振幅灵敏度。

1.2振动模型参数分析

二阶振动模型参数获取思路：① 据无阻尼条件下圆形固支板基频f1及等效质量Me1获得等效弹性系数Ke；② 据静压强p下挠度η1获得等效集中力Fe与声压p的关系式；③已知无阻尼等效质量Me1，再考虑液体对振动板的力抗Xr，获得液体介质中有阻尼的等效集中振动质量Me；④固支板在空气中的振动视为无阻尼振动[14]，液体力阻Rr即为集中参数系统等效力阻Re。将所得4参数Fe、Ke、Me、Re代入式(1)求得液体中共振频率f2及振幅η2。

由声学薄板振动理论，周边固支圆形薄板无阻尼振动基频[15]为

(2)

式中：a为圆形薄板半径；h为板厚，ρ为板密度；E为板杨氏模量；m为薄板质量；μ为泊松比。

(3)

已知静压强挠度公式[16]为

(4)

将式(3)、(4)代入Fe=Keη1得

(5)

式中：p为液体中声波声压；s为薄板面积。

液体对圆形固支板的阻抗[17](用中心速度等效，ka<1时)为

(6)

(7)

式中：ρ0为液体密度；c0为液体中声速；k为声波在液体中波数。

液体中振动等效集中质量为

(8)

1.3液体中共振频率及振幅灵敏度

小阻尼情况时由Ke、Me得液体中振动板的共振频率为

(9)

由此可见，共振频率推导结果与文献[18]一致。水与变压器油的声阻抗接近，选水介质参数按式(9)计算获得板的直径(D=2a)、厚度(h)与频率关系见图2。由图2看出，保持水中共振频率100 kHz不变时板厚随直径增大而增大(虚线)；采用虚线对应的一系列直径、厚度值可保证水中共振频率不变，但空气中自由频率远大于水中共振频率，且随直径减小厚度减小，差距增大。(振动板选光学玻璃薄板：杨氏模量E=57 GPa，泊松比μ=0.2，相对密度2.6)。

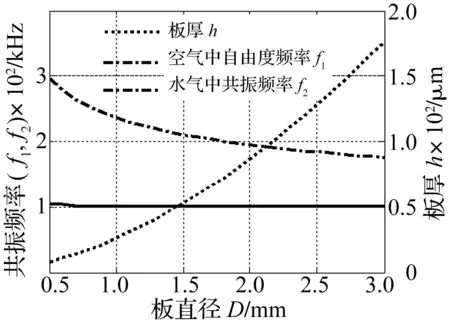
图2　水中固定共振频率100 kHz下厚度与直径关系Fig.2 Relationship between diameter and thickness at a fixed resonant frequency 100 kHz in water

二阶振动方程(1)对振幅的稳态解为

(10)

代入4个等效集中参数，获得传感器振动板尺寸与振幅灵敏度频响曲线，见图3。由3种尺寸数据仿真结果可见，取不同直径、厚度的振动薄板可保证水中共振频率100 kHz不变；保证共振频率相同时小直径、薄尺寸振动板振幅灵敏度更高。

图3　振幅灵敏度频率响应 Fig.3 Frequency response of amplitude sensitivity

2测试实验

2.1共振频率测量

受材料限制，实验中用直径2.52 mm玻璃管、厚度150 μm光学玻璃制作传感器样品。玻璃振动薄板在水中共振频率少许偏离100 kHz，仍可验证计算方法的正误。为增加测试信号强度，薄板镀银处理。

对振动板施加冲击，在小阻尼下振动板以共振频率振动。空气中用电子点火器放电产生冲击波，水中采用HB铅笔芯折断产生冲击波。用POLYTEC公司的OFV5000/OFV534激光测振仪测试薄板振动信号，结果见图4。由图4看出，空气中共振频率为205 kHz(计算值207 kHz)，水中共振频率为115 kHz (计算值114 kHz)，与式(9)计算结果一致。

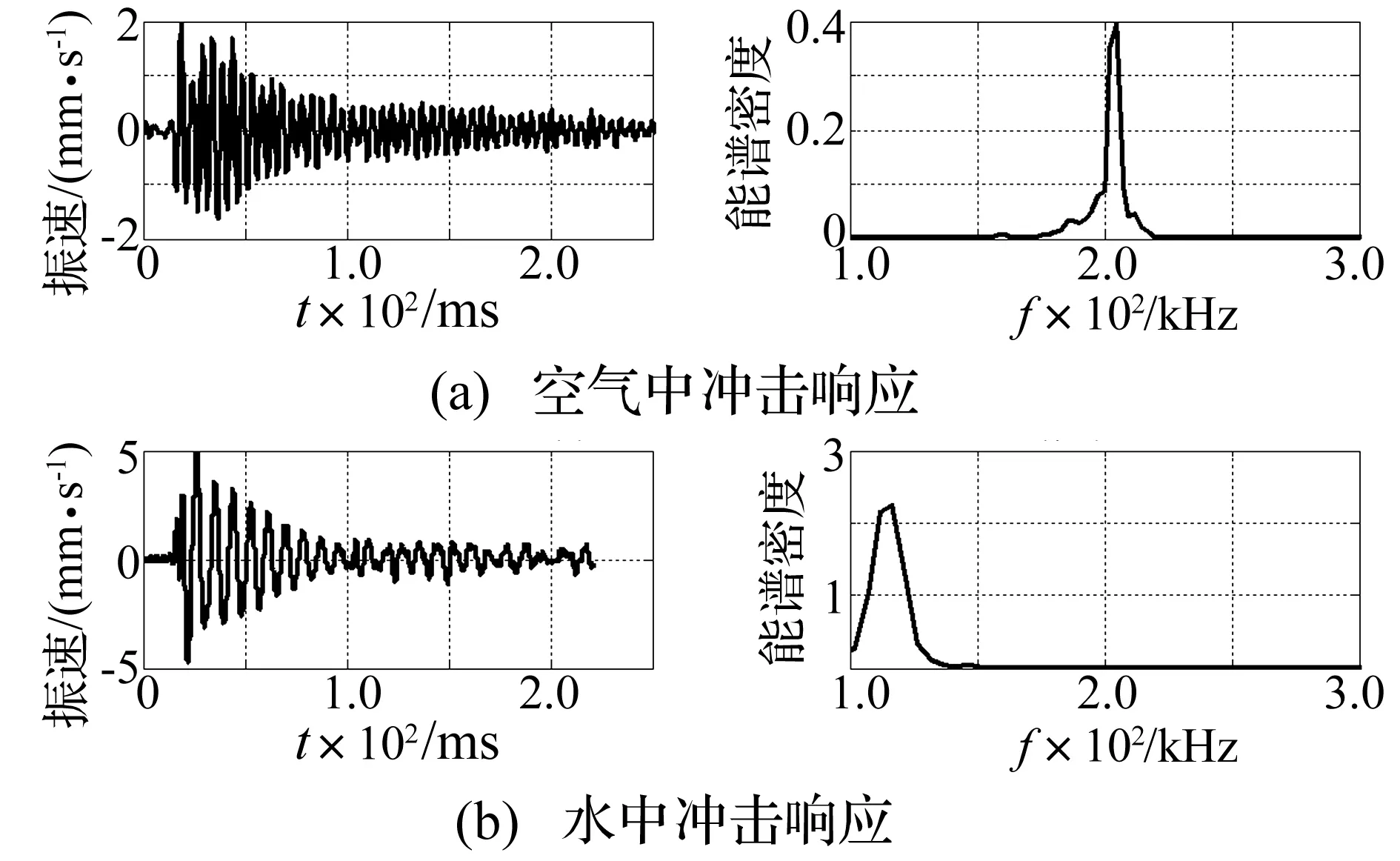
图4　共振频率测试结果Fig.4 Resonant frequency experiments

2.2振幅灵敏度频率响应测量

水箱中振幅灵敏度实验见图5。用信号发生器驱动压电声源产生声波，信号发生器每次输出10个正弦波信号，正弦波电压峰峰值为5 V，驱动信号频率可调。距声源16 cm处放置传感器样品及校准的压电声传感器测试样品处声压，激光测振仪(OFV5000/OFV534型，可测最小振幅在100 pm以下)透过水箱壁测试传感器振动薄板振幅。

图5　水中振幅灵敏度实验照片Fig.5 The photo of underwater amplitude sensitivity experiment

将所得传感器振幅值除以压电声传感器声压值获得传感器振幅灵敏度(实验中声压值约100 Pa)。振幅灵敏度实验结果及式(10)理论计算值见图6。由图6看出，水中振动板在共振频率115 kHz获得最大振幅灵敏度，与采用冲击法测试结果(图4)一致。实验结果中振幅灵敏度略高于理论值，且灵敏度曲线随频率偏离共振频率下降过程中有起伏现象。可能因实验水箱为有限尺寸，有一定反射噪声；被测样品安装支架及相邻压电声传感器对声波有反射作用，使被测样品未能处于理想自由声场，导致测试结果有起伏误差。由实验结果知，共振频率下振幅灵敏度约18 pm/Pa，而仅用静压力挠度式(4)计算为2.5 pm/Pa。说明振动薄板动、静态振幅差异较大，用二阶阻抗模型可计算液体中共振频率及振幅灵敏度。

图6　水中振幅灵敏度频率响应实验结果 Fig.6 Result for frequency response of amplitude sensitivity measurement in water

2.3局部放电测量

局部放电实验装置见图7。将制作的光纤FP传感器(D=2.52 mm,h=0.15 mm，R1=0.52，R2≈1，L=50 μm)与PAC公司的压电传感器(型号R15UG，配40 dB放大器)置于油介质中相同位置测试油隙击穿放电声波。针尖间隙约0.5～1 mm，用绝缘套管包裹用以衰减声信号，施加脉冲电源约50 kV。测试结果见图8。由图8看出，PAC的测试值为300～400 mV，系统灵敏度约20～28 mV/Pa (100～150 kHz)，被测声压约10～20 Pa，FP传感器测试值约200 mV，灵敏度为10～20 mV/Pa，FP本底噪声10～20 mV，系统最小可测试声压约1 Pa。

图7　局部放电测试实验照片Fig.7 The photo of experiment for partial discharges measurement

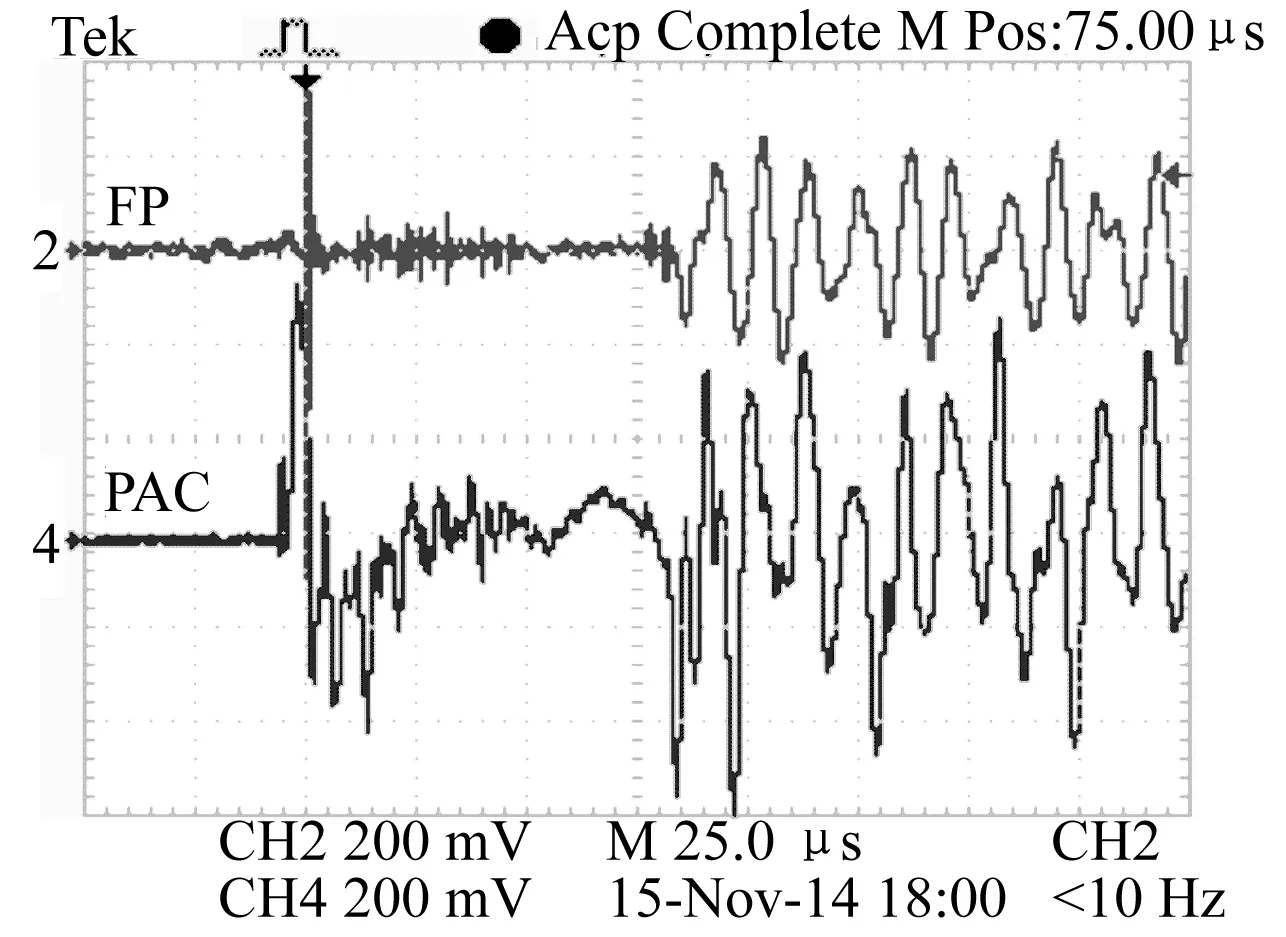
图8　局部放电测试结果Fig.8 The result ofpartial discharges measurement

3结论

通过集中参数二阶振动模型研究油浸变压器中非本征光纤法珀传感器的共振频率、振幅灵敏度与振动板尺寸关系,结论如下：

(1) 水中共振频率为100 kHz时振动板直径越小厚度应越薄，空气自由频率应大于100 kHz；振动板直径越小厚度越薄时，空气中自由频率大于100 kHz越多。

(2) 共振频率不变时，振动板直径越小厚度越薄，其振幅灵敏度越高。通过集中参数等效可正确计算液体中共振频率及振幅灵敏度。

(3) 研制的FP传感器对油中局部放电声波测试灵敏度较高，最小可测试声压约1 Pa。

参 考 文 献

[1] Jo W, Akkaya O C, Solgaard O, et al. Miniature fiber acoustic sensors using a photonic-crystal membrane [J]. Optical Fiber Technology, 2013, 19(6B): 785-792.

[2] 柯涛,朱涛,饶云江,等.基于空芯光子晶体光纤的全光纤法布里_珀罗干涉式加速度传感器[J].中国激光,2010, 37(1): 171-175.

KE Tao, ZHU Tao, RAO Yun-jiang,et al. Accelerometer based on all-fiber fabry-perot interferometer formed by hollow-core photonic crystal fiber [J]. Chinese Journal of Lasers, 2010, 37(1): 171-175.

[3] 王文辕,文建湘,庞拂飞,等.飞秒激光制备的全单模光纤法布里_珀罗干涉高温传感器[J].中国激光，2012,39(10): 85-89.

WANG Wen-yuan, WEN Jian-xiang, PANG Fu-fei, et al. All single-mode fiber fabry-perot interferometric hight temperature sensor fabricated with femtosecond laser [J]. Chinese Journal of Lasers, 2012, 39(10): 85-89.

[4] 朱佳利,王鸣,蔡东艳,等. 光纤法布里_珀罗微压传感器[J].光学学报,2014,34(4): 274-277.

ZHU Jia-li, WANG Ming, CAI Dong-yan, et al. A fiber fabry-perot micro pressure sensor[J]. Acta Optica Sinica, 2014, 34(4): 274-277.

[5] Yu B, Kim D W, Deng J D, et al. Fiber fabry-perot sensors for detection of partial discharges in power transformer [J]. Applied Optics, 2003, 42(16): 3241-3250.

[6] Wang X D, Li B Q, Xiao Z X,et al. An ultra-sensitive optical MEMS sensor for partial discharge detection [J]. Journal of Micromechanics and Microengineering, 2005,15(3): 521-527.

[7] Wang X D, Li B Q, Roman H T, et al. Acousto-optical PD detection for transformers[J]. IEEE Transactions on Power Delivery, 2006, 21(3): 1068-1073.

[8] 赵洪,李敏,王萍萍,等．用于液体介质中局放声测的非本征光纤法珀传感器[J].中国电机工程学报，2008,28(22): 59-63.

ZHAO Hong, LI Ming, WANG Ping-ping,et al. Extrinsic fiber fabry-perot sensors for pd-induced acoustic emission detection in liquid dielectrics [J]. Proceedings of the CSEE, 2008, 28(22): 59-63.

[9] 王伟,王赞,吴延坤,等.用于油中局部放电检测的Fabry-Perot光纤超声传感技术[J]. 高电压技术,2014, 40(3): 814-821.

WANG Wei, WANG Zan, Wu Yan-kun, et al. Fabry-Perot optical fiber ultrasonic sensing technology for detection of partial discharge in the oil [J]. High Voltage Engineering, 2014, 40(3): 814-821.

[10] 陈娜,丁悦通,孙庆国,等. 光纤法布里珀罗声发射传感系统[J]. 光通信技术,2010(3): 1-3.

CHEN Na, DING Yue-tong, SUN Qing-guo, et al. Fiber Fabry-Perot acoustic emission sensing system [J]. Optical Communication Technology, 2010(3): 1-3.

[11] 朱德恒,谈克雄,王昌长,等．在线检测变压器局部放电的微机系统[J]. 高电压技术,1992, 63(1):45-49.

ZHU De-huan, TAN Ke-xiong, WANG Chang-chang, et al. Computer-aided detection system for detecting partial discharge in power transformer[J].High Voltage Engineering,1992,63(1): 45-49.

[12] 周力行,何蕾,李卫国. 变压器局部放电超声信号特性及放电源定位[J]. 高电压技术,2003, 29(5): 11-15.

ZHOU Li-xing, He Lei, LI Wei-guo. Research on characteristics of ultrasonic signal of partial discharge and partial discharge sources location in transformer [J]. High Voltage Engineering, 2003, 29(5): 11-15.

[13] IEEE Std C57. 127-2007,IEEE guide for the detection and location of acoustic emissions from partial discharges in oil-immersed power transformers and reactors [S].

[14] 汤渭霖,范军．水中弹性结构声散射和声辐射机理-结构和水的声-振耦合作用[J].声学学报,2004,29(5):385-392.

TANG Wei-lin, FAN Jun. Mechanisms of sound scattering and radiation of submerged elastic structure-vibro-acoustic coupling of structure and water[J]. Acta Acustica, 2004, 29(5):385-392.

[15] 杜功焕,朱哲民,龚秀芬．声学基础[M]. 南京：南京大学出版社,2001:106-112．

[16] 陆明万,张雄,葛东云．工程弹性力学与有限元法[M].北京：清华大学出版社,2005: 132-135.

[17] 何祚镛,赵玉芳．声学理论基础[M].北京：国防工业出版社,1981:273-178．

[18] Mario D G. Flat and corrugated diaphragm design handbook (dekker mechanical engineering)[M]. New York: CRC Press, 1982: 196-197.

基金项目：国家自然科学基金项目(51375470)

收稿日期：2014-10-14修改稿收到日期：2015-01-30

通信作者韩立 男，博士，研究员，1970年9月生

中图分类号:TP212.14

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.02.026

Vibration characteristics of extrinsic fiber Fabry-Perot sensors

GUO Shao-peng1,2, FANG Guang-rong1,2, LIU Jun-biao1,2, JU Yu1

(1. Institute of electrical engineering, Chinese Academy of sciences, Beijing 100190, China;2. University of Chinese Academy of Sciences, Beijing 100049, China)

Abstract:Vibration characteristics are important for designing ultrasonic fiber Fabry-Perot (FP) sensors used for partial discharge detection. The vibrations of the film in sensors were simplified as the second order vibrations of lumped parametrers systems. The lumped parameters (mechanical impedance, equivalent mass, elastic coefficient, concentrated force) in second order vibration equations of the FP sensors in liquid were derived and the relationships between sensor’s resonant frequency, amplitude sensitivity and structure parameters were obtained. For a vibration plate with 2.52 mm-diameter and 150 μm-thickness in the sensor, the resonant frequency is 205 kHz in atmosphere and 115 kHz in water, and the amplitude sensitivity is about 18 pm/Pa at 115 kHz frequency in water. The minimum detectable acoustic pressure of the fabricated sensors is about 1 Pa.

Key words:partial discharge; ultrasonic sensor; lumped parameter; mechanical impedance; resonant frequency; frequency response

第一作者 郭少朋 男，博士生，助理研究员，1974年10月生