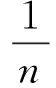PCA与SVD信号处理效果相似性与机理分析
聂振国, 赵学智
(华南理工大学 机械与汽车工程学院,广州 510640)
PCA与SVD信号处理效果相似性与机理分析
聂振国, 赵学智
(华南理工大学 机械与汽车工程学院,广州510640)
摘要:将主成分分析(Principal Component Analysis,PCA)用于信号处理,并与奇异值分解(Singular Value Decomposition,SVD)方法比较。分析总结PCA及SVD信号处理原理,提出基于PCA的特征值差分谱理论用于信号消噪。结果表明,PCA与SVD的处理效果较相似,相似性原因为原始矩阵右奇异向量即为协方差矩阵特征向量。SVD较PCA的重构误差小,因SVD无需计算协方差矩阵,可避免舍入误差产生。
关键词:主成分分析;奇异值分解;消噪;相似性;误差
主成分分析由Pearson[1]在生理学研究中用于分析数据及建立数理模型,通过对协方差矩阵进行特征分解[2],获得数据的主成分与权值。现PCA已用于地理、生物、经济、数理统计等众多领域。
奇异值分解理论由Beltrami提出,之后围绕奇异值分解算法已有诸多研究[3],如文献[4]提出的针对大型矩阵奇异值分解的多次分割双向收缩QR算法,能克服单向收缩QR算法收敛较慢、长时停滞甚至不收敛等缺陷,处理大型矩阵数值计算时具有迭代次数少、过程无停滞及收敛迅速等优点,SVD已广泛用于信号处理、图像压缩、数字水印、语音编码、控制系统等。
SVD与PCA的概念不同,应用领域、最终实现目标亦不同。PCA通过对多个样本构成的矩阵提取主成分进行降维,减小数据量以便于数据分析,且不会丢失原矩阵的主要特征;而SVD则通过对矩阵进行分解,选较奇异值进行重构获得原矩阵的主要信息,其中细节信息如噪声被滤掉。
关于SVD信号处理的文献较多[5-9],而关于PCA应用的文献尚少见。用信号构造Hankel矩阵作SVD处理,可据重构矩阵恢复出信号;而经PCA处理所得各主成分只代表原变量指标在新变量指标上所占比重,较原矩阵维数已降低,虽能保留原始数据的主要特征,无法从中恢复出原始数据。本文通过研究发现,PCA获得某一主成分后再乘以相应特征向量可得类似SVD的重构矩阵,且重构矩阵与SVD重构矩阵间有一一对应关系,信号处理效果相似,并对相似性进行分析、探讨。
1PCA与SVD基本理论
1.1基于PCA的信号处理原理

(1)
X可写成X=[x1x2… xm]。为消除量纲影响,将X化为零均值矩阵。
定义[10]:若x1,x2,…,xm为原变量指标,y1,y2,…,yl(l≤m)为新变量指标,则主成分分析即将m个原变量指标由l个新变量指标表示,即
(2)
式中:αij为系数,须满足
(3)
系数αij确定的原则如下:
(1) yi与yj(i≠j;i,j=1,2,…,l)相互无关;
(2) y1为x1,x2,…,xm的一切线性组合中方差最大者,y2为与y1不相关的x1,x2,…,xm所有线性组合中方差最大者。以此类推,yl为与y1,y2,…,yl-1均不相关的x1,x2,…,xm所有线性组合中方差最大者。则新变量指标y1,y2,…,yl分别称原变量指标x1,x2,…,xm的第1,2,…,l主成分。可证明αi=(α1i,α2i,,…,αmi)T为X协方差矩阵第i个特征值(从大到小排列)对应的特征向量[11]。可获得各主成分y1,y2,…,yl,若只用于数据降维分析,目的已达到,但若用于信号处理,则需重构矩阵,据前述有
yi=Xαi,(i=1,2,…,m)
(4)
(5)
由于X的协方差矩阵为半正定对称阵,其特征向量间相互正交,有
(6)
原矩阵X的重构表达式为
(7)
若选前l个主成分进行重构,则得近似矩阵为
(8)

1.2基于SVD的信号处理原理
奇异值分解指对任意矩阵A∈Rn×m总存在正交矩阵U∈Rn×n及V∈Rm×m使
A=USVT
(9)
式中:S=[diag(σ1,σ2, …,σr),0]或其转置,取决于n>m或n 设U=[u1,u2, …,un],V=[v1,v2, …,vn],其中ui∈Rn×1,vi∈Rm×1,则A可写成 A=σ1u1v1T+σ2u2v2T+…+σrurvrT (10) 令Ai=σiuiviT(i=1,2,…,r),按奇异值差分谱理论[13]选前l个分量进行重构,得近似矩阵为 (11) 获得近似重构矩阵后亦需据矩阵构造方式恢复出信号,如文献[7]中构造Hankel矩阵进行消噪处理,并给出具体信号恢复方法。 2PCA与SVD信号处理效果对比 2.1模拟信号去噪效果对比 2.1.1不含直流分量情况 以不含直流分量的模拟信号比较PCA与SVD的消噪效果,设信号为 f(t)=sin(2πt)+sin(4πt)+sin(20πt) (12) 对该信号以采样频率200 Hz、采样512点,并叠加服从N(0,1)的高斯白噪声,信噪比为1.705 3 dB,时域图见图1。以此信号构造257×256的Hankel矩阵X,矩阵行列数越相近,去噪效果越好[14]。PCA用于信号去噪时若据贡献率选主成分个数,由于矩阵维数较大,贡献率较高则主成分个数较多,会使去噪效果差。因此对PCA主成分个数采用类似SVD的奇异值差分谱理论选取,并称其为特征值差分谱理论。区别在于,PCA用协方差矩阵特征值,而SVD用矩阵本身奇异值。本例特征值序列及差分谱见图2(a),而奇异值序列及差分谱见图2(b)。由图2看出,奇异值较特征值大,但变化趋势相同。 图1 原始含噪信号Fig.1Theoriginalnoisysignal图2 PCA特征值曲线与SVD奇异值曲线及差分谱Fig.2EigenvaluescurveofPCAandsingularvaluescurveofSVDandthedifferencespectrum 据特征值差分谱理论选前6个主成分进行重构,获得去噪信号见图3(a),据奇异值差分谱理论选前6个分量进行重构,得去噪信号见图3(b)。由图3看出,二者消噪效果非常相似。 以模拟调幅信号为例对比两者消噪效果,设调幅信号为 y(t)=6sin(120πt+0.56)sin(12πt+0.78) (13) 叠加服从N(0,1)分布的高斯白噪声,信噪比为-4.194 1 dB。采样频率1 024 Hz,采样1 024点,其时域图见图4。 图3 模拟信号PCA与SVD去噪效果对比Fig.3ThePCAandSVDmethodde-noisingeffectofanalogsignal图4 含噪调幅信号Fig.4Thenoisyamplitudemodulationsignal 按文献[14],构造513×512的Hankel矩阵分别进行PCA、SVD处理,特征值序列、奇异值序列及差分谱见图5,消噪结果见图6。 图5 PCA特征值、SVD奇异值曲线及差分谱Fig.5 Eigenvalues curve of PCA and singular values curveof SVD and the difference spectrum 由图3、图6看出,PCA与SVD去噪效果几乎无差异,不易分辨,但实际上其处理结果误差却不同,对式(12)信号,可求得PCA法误差均值为0.146 7,SVD法误差均值为 0.129 0;而对式(13)调幅信号,PCA法误差均值为0.418 8,SVD法误差均值为0.389 1。可见SVD误差稍小。 PCA与SVD重构误差比较结果见表1及图7。可见,对每个信号,SVD重构误差均小于PCA。原因为PCA需计算协方差矩阵,且会产生舍入误差,而SVD直接对原矩阵进行处理,无需计算协方差矩阵,因而避免舍入误差。 表1 PCA与SVD重构误差 图6 调幅信号PCA、SVD法去噪效果对比Fig.6ThePCAandSVDmethodde-noisingeffectoftheamplitudemodulationsignal图7 PCA与SVD误差比较Fig.7TheerrorofPCAandSVD 2.1.2含直流分量情况 以含直流分量的模拟信号比较PCA与SVD的信号消噪效果,在模拟信号式(12)基础上叠加幅值为2的直流分量,得信号为 f=2+sin(2πt)+sin(4πt)+sin(20πt) (14) 对此信号以采样频率200 Hz、采样512点,并叠加服从N(0,1)的高斯白噪声。其时域图见图8。构造257×256的Hankel矩阵X,用PCA及SVD对此信号进行消噪,所得特征值序列及差分谱图见图9(a),奇异值序列及差分谱见图9(b)。对比图9、图2看出,加直流分量信号与未加直流分量信号的特征值差分谱图相同,而奇异值差分谱图变化较大。 图8 原始含噪信号Fig.8Theoriginalnoisysignal图9 PCA特征值曲线、SVD奇异值曲线及差分谱Fig.9EigenvaluescurveofPCAandsingularvaluescurveofSVDandthedifferencespectrum 添加直流分量后,虽Hankel矩阵每列均值增加2,但由于PCA进行零均值化处理,在零均值化过程中每列每个元素减去均值,因此,无论添加的直流分量幅值大小,最终所得特征值差分谱均与无直流分量特征值差分谱图相同。因此,利用特征值差分谱确定有用分量个数时,无论信号是否含直流分量均可简单以特征值差分谱最大峰值点确定有用分量个数,此为特征值差分谱理论。而按文献[13]奇异值差分谱理论,当用SVD进行信号消噪时,信号中若含直流分量,应剔除奇异值差分谱图中第1点影响,再取奇异值差分谱峰值最大点确定有用分量个数,以此进行矩阵重构。 据以上理论,此例中按照特征值差分谱理论,应选前6个分量进行重构,所得PCA去噪效果见图10(a);按奇异值差分谱理论用SVD去噪时,应选前7个分量进行重构方能获得较好去噪效果,见图10(b)。 2.2实际信号消噪效果对比 以某轴承振动信号为例,用PCA法、SVD法进行消噪。原始信号见图11,可见信号中有较大噪声污染。用PCA、SVD对其进行消噪处理,PCA特征值序列及差分谱见图12(a),SVD奇异值序列及差分谱见图12(b)。据差分谱理论,分别取前2个特征值、奇异值进行重构,所得重构结果见图13。可见,经PCA、SVD消噪后,信号已变干净,噪声完全消去。 图10 模拟信号PCA法与SVD法去噪效果对比Fig.10ThePCAandSVDmethodde-noisingeffectofanalogsignal图11 原始信号Fig.11Theoriginalsignal 图12 PCA特征值、SVD奇异值曲线及差分谱Fig.12 Eigenvalues curve of PCA and singular values curve of SVD and the difference spectrum 图13 实际信号PCA、SVD法去噪效果对比Fig.13 The PCA and SVD method de-noising effect of analog signal 3PCA、SVD信号处理效果相似原因分析 无论模拟信号或实际工程信号,由PCA、SVD重构结果看出两者相差无几。对该相似性的内在机理分析如下: PCA重构的某分量可写为 Xi=yiαiT=XαiαiT (15) SVD某分量形式为 (16) (17) 对比式(15)、(17)知,PCA、SVD所得分量矩阵Xi具有相似形式,但存在向量αi与vi的区别。分析αi与vi的关系,X的协方差矩阵为 式中:cov(xi,xj)=E[(xi-E(xi))(xj-E(xj))]。 X的奇异值分解为 X=USVT (19) 据式(19)可得 XTX=(USVT)TUSVT= VSTUTUSVT=VSTSVT (20) (21) 据式(21)可知X的右奇异向量vi即为XTX的特征向量,而X奇异值的平方即为XTX的特征值。对X进行零均值处理后,有E(xi)=0(i=1,2,…m),因此X的协方差矩阵可写为 (22) αi=vi (23) 结合式(15)、(17)、(23)可见,PCA及SVD所得重构矩阵Xi相等,此为PCA及SVD的消噪效果相似性的本质原因;但PCA需计算协方差矩阵,存在数据舍入误差,而SVD无需计算协方差矩阵,且无需进行零均值化处理,SVD计算量少,能避免计算协方差矩阵的舍入误差,相对误差较小。而PCA在处理带直流分量的信号时,因其进行零均值化处理时能消除直流分量影响,故无、有直流分量的特征值差分谱完全相同,即无需考虑有无直流分量。 由此可见,虽PCA、SVD信号处理效果相似,但SVD处理结果误差较PCA小,且SVD计算量少,故工程实际应用中应用SVD去噪。 4结论 通过分析PCA、SVD信号处理算法,并实例对比,结论如下: (1) 两者结果相似原因为原始矩阵右奇异向量即为协方差矩阵特征向量。信号中含直流分量、用PCA去噪时,特征值差分谱与无直流分量相同,只需据特征值差分谱最大峰值确定有用分量个数,无需考虑信号有无直流分量。 (2) SVD误差较PCA小的原因为,PCA在计算协方差矩阵时会产生舍入误差,而SVD无需计算协方差矩阵,避免舍入误差产生。 参 考 文 献 [1] Pearson K. On lines and planes of closest fit to systems of points in space[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science,1901,2(11): 559-572. [2] Abdi H, Williams L J. Principal component analysis[J]. Wiley Interdisciplinary Reviews: Computational Statistics, 2010, 2(4): 433-459. [3] Stewart G W. On the early history of the singular value decomposition[J]. SIAMReview, 1993, 35(4): 551-566. [4] 赵学智,叶邦彦,陈统坚. 大型矩阵奇异值分解的多次分割双向收缩 QR算法[J]. 华南理工大学学报:自然科学版, 2010, 38(1):1-8. ZHAO Xue-zhi, YE Bang-yan, CHEN Tong-jian. Multi-partition and double-direction shrink QR algorithm for singular value decomposition of large-scale matrix[J]. Journal of South China University of Technology: Natural Science Edition, 2010, 38(1): 1-8. [5] 赵学智,叶邦彦,陈统坚. 基于 SVD 的奇异性信号检测原理及其应用[J]. 振动与冲击, 2008, 27(6): 11-14. ZHAO Xue-zhi, YE Bang-yan, CHEN Tong-jian. Principle of singularity detection based on SVD and its application[J]. Journal of Vibration and Shock, 2008, 27(6): 11-14. [6] 段向阳,王永生,苏永生.基于奇异值分解的信号特征提取方法研究[J]. 振动与冲击, 2009,28(11): 30-33. DUAN Xiang-yang, WANG Yong-sheng, SU Yong-sheng. Feature extraction methods based on singular value decomposition[J]. Journal of Vibration and Shock, 2009,28(11): 30-33. [7] 张波,李健君. 基于Hankel 矩阵与奇异值分解 (SVD) 的滤波方法以及在飞机颤振试验数据预处理中的应用[J]. 振动与冲击, 2009, 28(2): 162-166. ZHANG Bo, LI Jian-jun. De-noising method based on hankel matrix and SVD and its application in flight flutter testing data preprocessing[J]. Journal of Vibration and Shock, 2009,28(2): 162-166. [8] 陈恩利,张玺,申永军,等. 基于SVD降噪和盲信号分离的滚动轴承故障诊断[J]. 振动与冲击, 2012, 31(23): 185-190. CHEN En-li, ZHANG Xi, SHEN Yong-jun, et al. Fault diagnosis of rolling bearings based on SVD denoising and blind signals separation[J]. Journal of Vibration and Shock, 2012,31(23): 185-190. [9] 王建国,李健,刘颖源. 一种确定奇异值分解降噪有效秩阶次的改进方法[J]. 振动与冲击, 2014(12): 176-180. WANG Jian-guo, LI Jian, LIU Ying-yuan. An improved method for determining effective order rank of SVD denoising[J]. Journal of Vibration and Shock, 2014(12): 176-180. [10] 王峻峰. 基于主分量独立分量分析的盲信号处理及应用研究[D]. 武汉:华中科技大学, 2005. [11] Liang Y C, Lee H P, Lim S P, et al. Proper orthogonal decomposition and its applications-part I: theory[J]. Journal of Sound and Vibration, 2002, 252(3): 527-544. [12] Golub G H, Van Loan C F,袁亚湘. 矩阵计算[M]. 北京:人民邮电出版社, 2011. [13] 赵学智,叶邦彦,陈统坚. 奇异值差分谱理论及其在车床主轴箱故障诊断中的应用[J].机械工程学报,2010(1):100-108. ZHAO Xue-zhi, YE Bang-yan, CHEN Tong-jian. Difference spectrum theory of singular value and its application to the fault diagnosis of headstock of lathe[J]. Journal of Mechanical Engineering,2010 (1): 100-108. [14] 赵学智,叶邦彦,陈统坚. 矩阵构造对奇异值分解信号处理效果的影响[J]. 华南理工大学学报:自然科学版, 2008, 36(9):86-93. ZHAO Xue-zhi, YE Bang-yan, CHEN Tong-jian. Influence of matrix creation way on signal processing effect of singular value decomposition [J]. Journal of South China University of Technology: Natural Science Edition, 2008, 36(9): 86-93. 基金项目:国家自然科学基金项目(51375178);广东省自然科学基金项目(S2012010008789) 收稿日期:2014-11-19修改稿收到日期:2015-01-20 通信作者赵学智 男,教授,博士生导师,1970年11月生 中图分类号:TN91117; TH16513 文献标志码:A DOI:10.13465/j.cnki.jvs.2016.02.003 Similarity of signal processing effect between PCA and SVD and its mechanism analysis NIE Zhen-guo, ZHAO Xue-zhi (School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640, China) Abstract:The principal component analysis (PCA) was applied to signal processing and its effect was compared with that of the singular value decomposition (SVD). The signal processing principles of PCA and SVD were analyzed and summarized, and the theory of eigenvalues difference spectrum based on PCA for signal denoising was introduced. It is pointed out that PCA has a very similar signal processing effect to that of SVD when applied to signal de-noising. The reason for this similarity was analyzed theoretically, and it is found that this is because the right singular vectors of the original matrix are just the eigenvectors of its covariance matrix, and leads to the similarity between PCA and SVD in signal processing. It is also pointed out that the reconstruction error of SVD is smaller than that of PCA, and the reason is that SVD does not need to compute the covariance matrix, so the rounding errors are avoided. Key words:principal component analysis; singular value decomposition; de-noising; similarity; error 第一作者 聂振国 男,硕士生,1991年10月生