基于DFM/FEM铝蜂窝夹层结构耦合损耗因子预测

孔宪仁, 王英诚 ， 张红亮

(1. 哈尔滨工业大学 卫星技术研究所，哈尔滨　150080；2. 北京强度环境研究所，北京　100076；3.中国空间技术研究院 航天东方红卫星有限公司，北京　100010)



基于DFM/FEM铝蜂窝夹层结构耦合损耗因子预测

孔宪仁1, 王英诚2， 张红亮3

(1. 哈尔滨工业大学 卫星技术研究所，哈尔滨150080；2. 北京强度环境研究所，北京100076；3.中国空间技术研究院 航天东方红卫星有限公司，北京100010)

摘要：在使用统计能量分析对复杂的蜂窝夹层结构进行高频动力学响应预示的关键环节之一在于准确估算耦合损耗因子。研究应用对偶模态/有限元法(DFM/FEM)估算铝蜂窝夹层结构之间的耦合损耗因子，通过算例对该方法进行仿真验证，结果表明，该方法可行且高效准确。最后对L型耦合铝蜂窝夹层板结构进行振动实验，并使用功率输入法辨识试件间的耦合损耗因子，比较功率输入和和对偶模态/有限元法结果，两者一致性好，进一步验证了对偶模态/有限元法估算铝蜂窝夹层板系统耦合损耗因子的可行性，扩展了统计能量分析在复杂结构上的应用。

关键词：统计能量分析；对偶模态法；耦合损耗因子；铝蜂窝夹层板

应用统计能量分析(SEA)对复杂结构进行高频动力学响应预示时，关键在于确定统计能量分析参数，特别是准确估算出结构间的耦合损耗因子(CLF)。目前，对于绝大多数工业结构而言，CLF往往通过实验辨识。在实验统计能量分析方面，最为经典的无疑是功率输入法(PIM)，许多学者对其进行了研究与验证，其中，Bies等[1]利用功率输入法实验估计了两块耦合的板结构的损耗因子矩阵，并对随机选择的激振点数目对输入功率的影响进行了深入的研究。Lalor[2]对PIM的能量矩阵的组装方式进行了改进，将耦合损耗因子和内损耗因子分离求解，以实现对计算的简化，并且在一定程度上提高了估算精度。虽然PIM已经得到广泛的认可，但其要求实体的结构，步骤繁琐，随着子系统数量的增加容易出现病体矩阵等问题，对于讲究高效迅速的今天，难以满足在产品设计初期进行结构动力学高频环境预示的要求。

蜂窝夹层结构由较薄的面板与较厚的芯子胶接而成。在弯曲荷载作用下，面板主要承担拉压应力，蜂窝芯主要承担剪切应力，因其具有极高的刚质比、抗失稳能力强、耐疲劳以及隔热等诸多优点被广泛用于航天航空领域[3]。目前，蜂窝夹层结构的模态密度已经具有理论公式[4-6]。对于阻尼损耗因子而言，虽然阻尼机制复杂，但在以往试验结果和理论分析对比的基础上逐渐对阻尼的分布也有了定性的认识[7]。而准确估算出蜂窝夹层结构之间的CLF仍旧非常困难。因此，寻找新的估算在设计初期准确估算出铝蜂窝夹层板结构间的CLF的方法对于扩展SEA在航天航空领域的应用来说意义重大。

基于上述介绍，本文提出应用对偶模态法/有限元(DFM/FEM)估算铝蜂窝夹层板结构间的CLF。首先，给出对偶模态法的理论推导。其次，通过数值仿真验证该方法的正确性。最后，对L型铝蜂窝板耦合结构进行振动实验，对比分析实验和DFM/FEM的辨识结果。

1统计能量分析

统计能量分析(SEA)始于在20世纪60年代[8]，用于计算耦合的子系统之间的功率流传递。如图1所示，假定功率Piin输入至一个子系统i时，只能通过子系统i耗散或传递给耦合的子系统j。功率流平衡等式为：

Piin=Pidiss+Pij

(1)

耗散功率和传递功率可以使用子系统能量Ei来表示。

(2)

式中:Piin是子系统i的输入功率，ηi为子系统i的阻尼损耗因子，ηij是子系统i和子系统j之间的耦合损耗因子，ωc是分析带宽的中心角频率。耦合损耗因子满足互易性关系：

niηij=njηji

(3)

式中:ni和nj分别为子系统i和j的模态密度。

图1　二子系统SEA模型Fig.1 Two-Subsystem SEA Model

2对偶模态法

2.1基本原理

对偶模态法最初由Maxit等[9-10]提出，该方法基于一组应力位移对偶模态方程，通过非标准的模态扩展，利解耦子系统的模态去描述解耦子系统的自由振动。如图2所示，对耦合的二子系统SEA模型进行解耦分析，其中一个子系统的耦合边界面受档，它的响应通过应力模态振型表示。另外一个子系统耦合边界面自由，它的响应通过位移模态振型表示。这时，子系统1和子系统2之间的模态功率流平衡方程可以写成类似于SEA基本等式的形式：

(4)

图2　对偶模态法原理Fig.2 Principle of dual formulation method

(5)

(6)

两个子系统之间的功率流为模态与模态之间的功率流的总和，即：

(7)

根据模态能量均分假设：

(8)

由式(7)与式(8)可以得到：

(9)

其中:耦合损耗因子η12为：

(10)

(11)

式中：N1,N2为子系统分析带宽的共振模态数。

3铝蜂窝夹层板等效理论

蜂窝夹层结构动力学机制复杂，难以像均值板一样推导出结构动力学方程，在早期的蜂窝复合夹层结构分析模型中，由于芯层相对于面板较软，为了简化计算，常常忽略芯层的面内刚度和弯曲刚度。如图3所示，将蜂窝夹层等效为各向异性板，等效参数可以由式(12)得到。

(12)

图3　蜂窝夹层结构Fig.3 Honeycomb sandwich construction

事实上，芯层相对于面板而言却有较大的厚度，因此忽略其面内刚度和弯曲刚度必然会带来不可忽视的误差。

图4　蜂窝夹层结构Fig.4 Honeycomb sandwich construction

如图4所示，蜂窝胞元的变形为：

P=σ1(h+lsinθ)b

(13)

式中:b为壁板的宽度。

(14)

(15)

x,y方向上的等效应变：

(16)

等效泊松比：

(17)

X方向的杨氏模量：

(18)

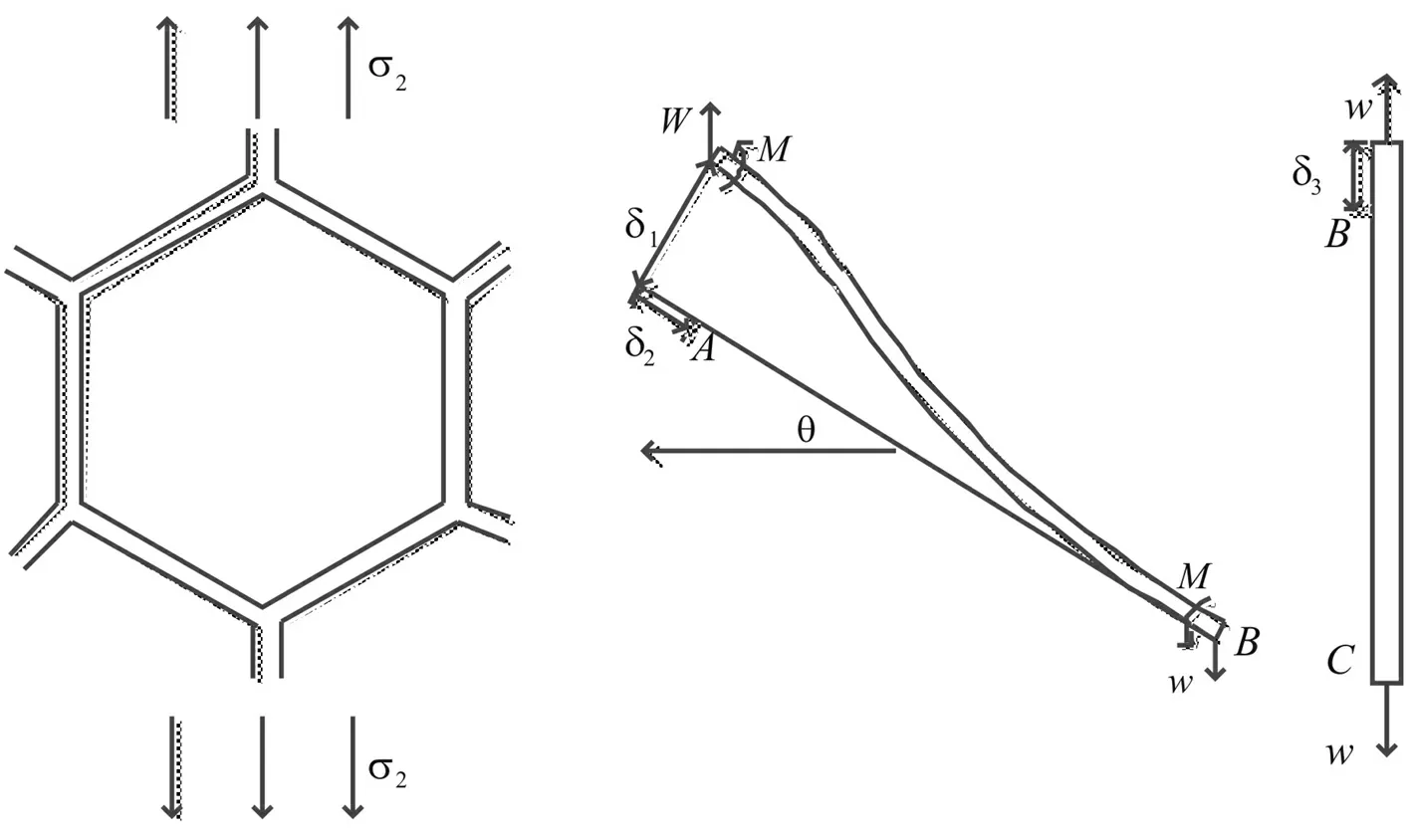
图5　蜂窝夹层结构Fig.5 Honeycomb sandwich construction

如图5所示，蜂窝胞元的变形为：

(19)

斜壁板AB的挠度为：

(20)

斜壁板AB伸长量:

δ2=Wsinθl/(Esbt)

(21)

铅直壁板BC的伸长量:

δ3=Wh/(Esbt)

(22)

x,y方向上的等效应变：

(23)

等效的泊松比:

(24)

y方向的杨氏模量

(25)

等效的横向剪切模量:

(26)

蜂窝芯的等效密度为：

(27)

式中:ρs为蜂窝壁材料容重，ts蜂壁厚度，d,c为蜂窝格边长，θ蜂窝壁内角的一半。

三明治夹芯板理论将蜂窝夹芯等效为正交各向异性的均匀连续结构，考虑了蜂窝芯子形状对蜂窝夹层板整体性能的影响特性，使得这种等效理论更符合实际情况。对于正六边形蜂窝芯，蜂窝芯的等效参数可以通过下式获得[11]：

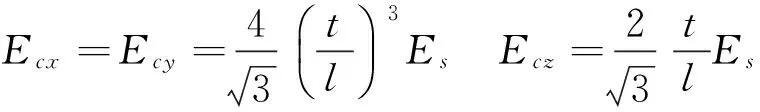
(28)

式中:γ是修正系数，一般取0.4～0.6，理论值取1。Es,Gs,ρs,μs分别代表蜂窝芯子的材料的弹性模量，剪切模量，密度以及泊松比。

4算例仿真

考虑两块铝蜂窝夹层板组成L型耦合结构，其中蜂窝夹芯为正六边，面板材料为铝材，蜂窝芯为铝箔，弹性模量为72 GPa，泊松比0.33，密度为2 700 kg/m3，蜂窝夹芯壁厚0.04 mm，壁长4 mm，其中，小板长1.5 m，宽1 m，面板厚度为0.5 mm，蜂窝芯层为8 mm。大板长为2.5 m，宽为1 m，面板厚度为0.5 mm，蜂窝芯层为24 mm，假设阻尼损耗因子均为η1=η2=0.04。

根据三明治夹心板等效理论，由式(28)可以得到蜂窝芯层的等效参数,示于表1。

表1　蜂窝芯等效参数

(29)

我们使用SEA数值实验[12]和VA-one软件的数值仿真结果作为对比验证。其中，SEA数值实验计算CLF的原理是通过有限元建模进行数值实验，利用外部激励作用下耦合子系统的能量比与耦合损耗因子之间的关系求得，属于模态方法。VA-one估算铝蜂窝夹层板之间的CLF是将蜂窝夹层结构进行等效后采用基于半无限子系统假设的波方法估算CLF。两者均是估计耦合损耗因子的有效方法，但对于蜂窝夹层结构复杂，波方法在对其进行等效估算时误差相对较大。

如图6所示，为模拟模态不相关激励，对小板随机选取五个节点进行激励，求各板在均方根为1的随机力激励作用下的响应。需要说明的是，使用有限元进行高频动力学响应分析时，有限元网格必须足够细密才能捕捉到高频模态，一般来说，有限元网格应该小于波长的八分之一。即便如此，有限元分析结果仍旧会出现特征频率和模态阵型漂移等问题，但误差会随着多个激振点平均而减小。

图6　数值实验示意图Fig.6 sketch of numerical experiment

根据随机振动理论可以得到随机作用下得到子系统的均方能量响应。此时，两个子系统的SEA功率流平衡方程为：

(30)

根据式(14)中的第二个式子可以得到：

(31)

式中:〈Ei〉是激励作用下铝蜂窝板i响应能量，n1,n2是三分之一倍频内的模态密度。

铝蜂窝夹层板的模态密度可以由Erickson[11]公式得到：

(32)

式中:a,b为蜂窝夹层板的长和宽，Ef,μ,tf,tc为蜂窝夹层板面板的弹性模量、泊松比、厚度以及蜂窝夹心层的厚度。m为整个蜂窝夹心板的单位面积质量，f为频率。

(33)

(34)

(35)

(36)

假设小板为子系统1大板为子系统2，对模型分别使用三种方法进行仿真，仿真结果如图7所示所示。对偶模态法、Va-one和SEA数值实验三种方法的结果趋势相同，子系统之间的耦合损耗因子随着频率的升高而减小，同时可以看出，DFMFEM法的估算值与SEA数值实验的匹配度要好于Va-one的估算值与SEA数值实验的匹配度，故可以证明DFMFEM法能够更加准确地估算铝蜂窝夹层板结构间的耦合损耗因子，并且相对于SEA数值实验，该方法具有步骤简单，计算量等优点。

图7　耦合损耗因子Fig.7 Coupling loss factor

接下来，进一步探讨对偶模态法是否适用于复杂蜂窝壳结构的情况。如图8所示，一个半圆柱铝蜂窝夹层壳体与一块铝蜂窝夹层壳体平板耦合连接，其中半圆柱的曲率半径为1.5 m，高为3 m，蜂窝夹层总厚度为24 mm面板厚度为0.5 mm，面板的材料为铝，蜂窝芯夹层材料为铝箔。底板几何形状为半圆板，面板厚度为0.5 mm铝板。蜂窝夹层厚度为14 mm，材料为铝箔。蜂窝夹心的形状均为正六边形，蜂窝壁厚0.04 mm，蜂窝壁长4 mm。材料参数为：弹性模量为72 GPa，泊松比0.33，密度为2 700 kg/m3。

图8　铝蜂窝壳结构示意图Fig.8 Illustration of aluminum honeycomb sandwich shell

对解耦子系统分别进行有限元分析，其中铝蜂窝半圆柱壳体耦合边界自由，提取位移模态振型。铝蜂窝半圆板耦合边界受档，提取应力模态振型。使用对偶模态法对辨识该结构子系统之间的耦合损耗因子，结果图9所示。

从结果可以看出，对偶模态法的估算值与Va-one的估算值在趋势吻合且未出现较大误差，数量级相同，整体上，两种方法的估算结果在大于400 Hz时具有很好的一致性。η12均大于η21。铝蜂窝壳(子系统2)的模态密度要大于铝蜂窝板(子系统1)，根据互易性关系可知，η12在理论上应该大于η21，仿真结果合理。

故此，可以证明DFMFEM法可以正确地估算出更为复杂的蜂窝夹层板壳结构之间的耦合损耗因子，为对偶模态法在工程实际中的应用奠定了基础。

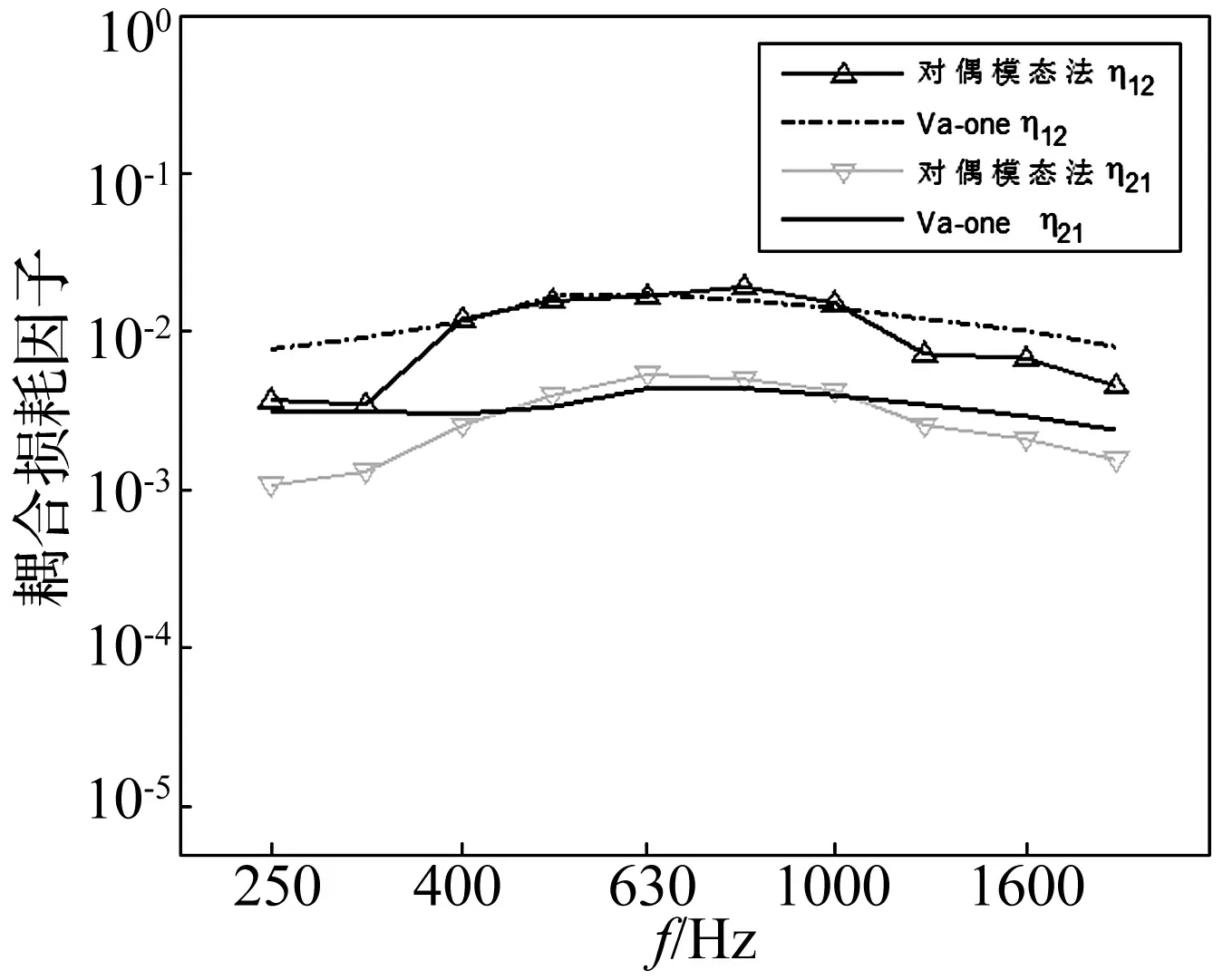
图9　耦合损耗因子Fig.9 Coupling loss factor

5实验验证

对L型铝蜂窝板耦合结构的实验模型进行振动实验与分析，实验试件如图10所示。

图10　实验试件Fig.10 Structure for Experiment

试件由两块铝蜂窝夹层板组成L型耦合结构，小板尺寸为120 mm×130 mm，上下面板厚度均为1 mm，中间夹层厚度为8 mm。大板的结构尺寸为120 mm×140 mm，上下面板厚度均为1 mm，中间夹层厚度为13 mm。公共边处通过11个铁角码及对应的44个螺栓连接而成，面板为铝质材料，两块板的蜂窝夹芯均为正六边形铝箔，蜂窝壁厚为0.06 mm，长为4 mm。材料属性为：弹性模量E=7 200 MPa，密度为2.7×103kg·m-3、泊松比为0.33

实验装置如图11所示，用到的设备包括激振器(JZQ50)、任意波形发生器(Agilent33250A)、加速度传感器(333B30)，阻抗头(288D01)，功率放大器(DH5801)以及数据采集系统(JAGUAR)组成。实验现场如图12所示。

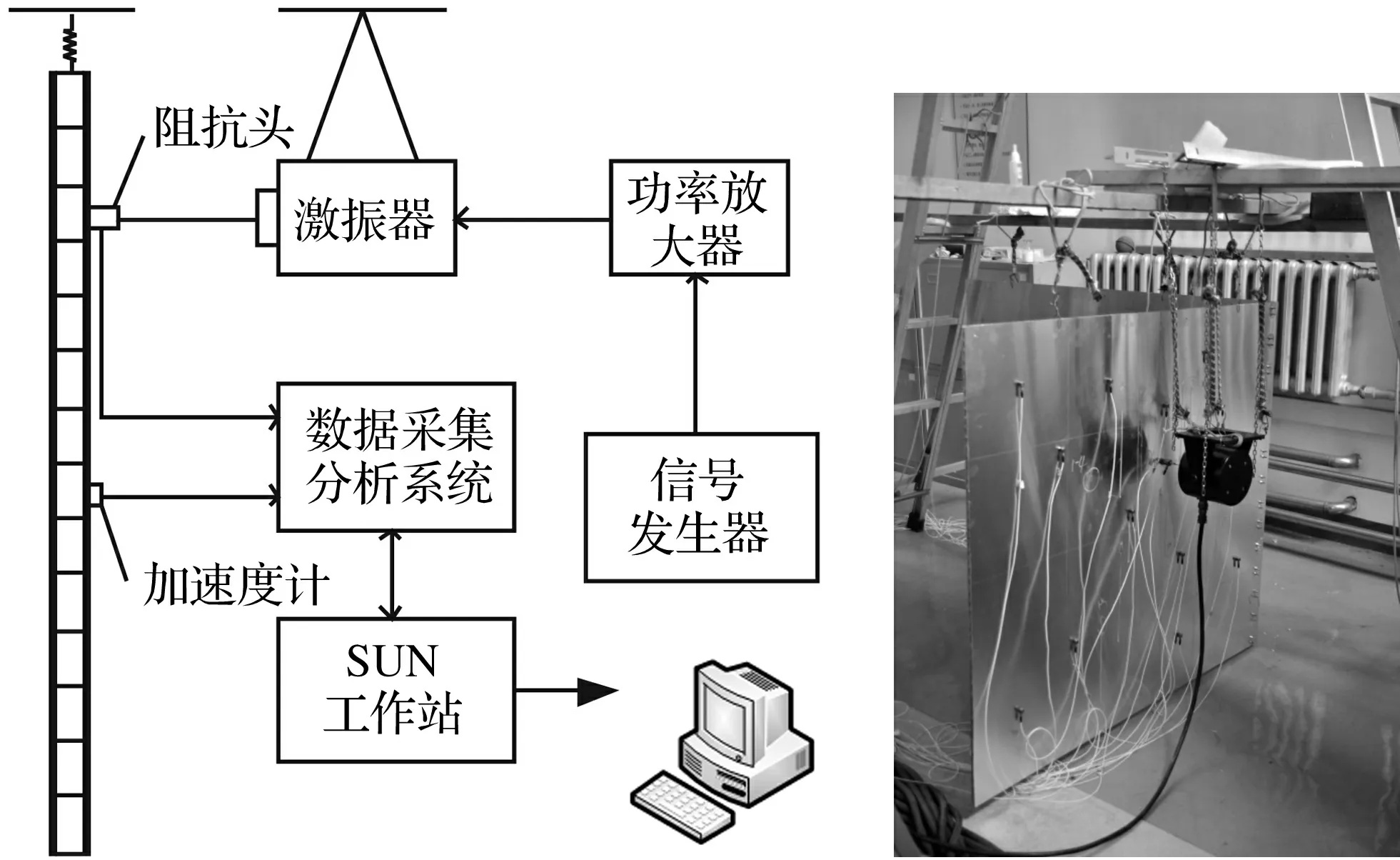
图11 实验装置示意图Fig.11Sketchmapoftestsetup图12 实验照片Fig.12Photooftest

为得到较好的空间平均数据，每块铝蜂窝板随机选择5个激振点，小板随机布置13个加速度测点，大板随机布置15个加速度测点。测试时，将试件和激振器使用弹性绳悬挂起来，激振力由信号发生器中的随机白噪声信号经功率放大器作用后驱动激振器产生。

作为实验验证， 使用经典的功率输入法作为实验

辨识方法，实验辨识需要的数据包括稳态激励作用下各子系统的平均输入功率和响应能量。其中单点输入功率可以通过连接于激振器的阻抗头所测量的力和加速度的互谱得到，理论公式[13]如式(37)所示，铝蜂窝板的输入功率由5点平均得到。

(37)

式中:F为激振力f(t)的傅里叶变换，Y为激励点的点导纳，Sfa(ω)为激振力和加速度的互谱密度。

振动能量分别由各蜂窝板的所有测点(激振点处除外)的估算值平均得到，公式如式(38)所示。

(38)

式中:Saa(ω)为加速度自功率谱密度。

将计算得到的振动能量对输入功率进行归一化平均，图10为小板受到激振并进行平均处理后，中心频率为315 Hz～3 125 Hz的连续三分之一倍频程带宽内两块铝蜂窝板的平均能量。

使用对偶模态法辨识实验试件之间的耦合损耗因子，在解耦分析中，小板耦合边界受档，大板耦合边界条件自由，阻尼由实验测得。实验及DFMFEM法辨识计算分别在连续的三分之一倍频程分析带宽内进行，分析频带的中心频率取315 Hz～4 000 Hz。实验结果和仿真和仿真结果如图14和图15所示。

DFMFEM法的估计结果与实验结果较低频率域还是存在较大的误差，究其原因，如图16所示，在频域较低时，铝蜂窝夹层板的模态密度较低，模态数小于5，模态能量均分假设难以满足，但这时SEA理论是否成立也需要进一步研究。由图14和图15可以看出，随着频率的升高，DFMFEM法的估算值与实验结果吻合度越来越高，在频率大于1 000 Hz的频域内，两者在个别频带内误差有所增加，但并不明显(小于3 db)。与此同时，DFMFEM法的估算结果与实验结果的匹配度要好于VA-one仿真结果与实验结果的匹配度。

图13 稳态激励时子系统归一化平均能量Fig.13Normalizedaveragesofsubsystemenergiesundersteadystateexcitation图14 耦合损耗因子Fig.14Couplinglossfactor图15 耦合损耗因子Fig.15couplinglossfactor

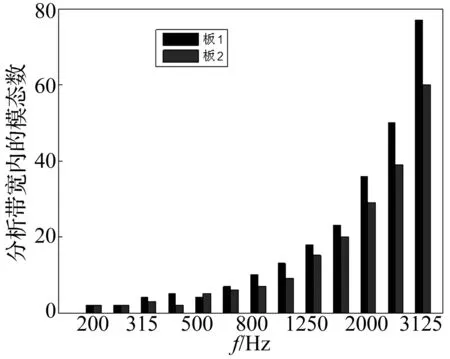
图16　三分之一倍频程内板的模态数Fig.16 Number of modes of plates in third octive frequency band

6结论

由仿真和实验结果可以得出：DFMFEM法能有效估算铝蜂窝夹层板结构之间的CLF。与传统的数值实验方法相比，DFMFEM法更加简单高效，不需要求解运动方程，仅需根据解耦蜂窝夹层结构耦合边界节点上的振动模态振型便可直接估算出CLF。将该法预测的CLF与VA-one、AutoSEA2等统计能量分析软件结合进行建模仿真，可以提高预示的精度和准确性，这对于扩展SEA在工程实际中的应用具有极其重要的意义，

本文的研究结果可以作为进一步DFMFEM法估算蜂窝夹层结构之间CLF的基础，仍需要对更为复杂的结构进行研究和验证。

参 考 文 献

[1] Bies D A, Hamid S. In situ determination of loss and coupling loss factors by the power injection method[J]. Journal of Sound and Vibration, 1980, 70(2): 187-204.

[2] Lalor N. The experimental determination of vibrational energy balance in complex structures [C]// Proceedings SIRA Conference on Stress and Vibration. London, 1989:108-429.

[3] 张广平, 戴干策. 复合材料蜂窝夹芯板及其应用[J]. 纤维复合材料,2000(2): 25-27.

ZHANG Guang-ping, DAI Gan-che. Honeycomb sandwich panels panels of composites and their application[J]. Fiber Composites,2000(2): 25-27.

[4] Wilkinson J P D. Modal densities of certain shallow structural elements[J]. Joumal of Acoustical Society of America,1968(43): 245-251.

[5] Renji K, Nair P S, Narayanan S. Modal density of composite honeycomb sandwich panels[J]. Journal of Sound and Vibration, 1996(195): 687-699.

[6] Erickson L L. Modal density estimates for sandwich panels. Theory and experiment[R]. NASA TND-5771, 1979.

[7] 韩增尧, 曲广吉. 航天器宽频随机振动响应分析[J]. 中国空间科学技术,2002(2):24-40.

HAN Zeng-yao, QU Guang-ji. Study of wide-band random vibration response prediction for the spacecraft structures[J]. Structure & Environment Engineering,2002(2):24-40.

[8] 姚德源, 王其政. 统计能量分析原理及其应用[M].北京：北京理工大学出版社，1995.

[9] Maxit L, Guyader J L. Estimation of SEA coupling loss Factors using a dual formulation and FEM modal information, partⅠ: Theory[J]. Journal of Sound and Vibration,2001, 239(5): 907-930.

[10] Maxit L, Guyader J L. Estimation of SEA coupling loss Factors using a dual formulation and FEM modal information, partⅡ: Numerical applications[J]. Journal of Sound and Vibration,2001, 239(5): 931-948.

[11] 富明慧, 伊久仁. 蜂窝芯层的等效弹性参数[J]. 力学学报, 1999, 31(1): 113-118.

FU Ming-hui, YIN Jiu-ren. Equivalent elastic parameters of the honeycomb core [J]. Acta Mechanica Sinica,1999,31(1): 113-118.

[12] Lyon R H. Statistical energy analysis of dynamical systems: theory and applications[M]. Cambridge, Mass, MIT Press, 1975.

[13] 乔百杰，赵彤，陈雪峰.功率流测量以及振动能量参数估计试验研究[J].振动与冲击,2014,33(7):194-198.

QIAO Bai-jie，ZHAO Tong，CHEN Xue-fen. Tests for power flow measurement and vibrational energy estimation [J]. Journal of Vibration and Shock,2014,33(7):194-198.

收稿日期：2014-07-04修改稿收到日期：2015-09-06

通信作者王英诚 男，助理工程师，1989年生

中图分类号:V416.2；TB533

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.01.021

Coupling loss factors estimation of aluminum honeycomb sandwich structures using DFM/FEM

KONG Xian-ren1, WANG Ying-cheng2, ZHANG Hong-liang3

(1. Research Institute of Satellite Technology, Harbin Institute of Technology, Harbin 150080, China; 2. Beijing Institute of Structure & Environment Engineering, Beijing 150080, China; 3. Aerospace Dongfanghong Satellite Co., LTD, China Aerospace Science and Space Technology Institute, Beijing 100010, China)

Abstract:The accurate estimate of coupling loss factor is one of key steps in a SEA prediction for high frequency dynamic responses of honeycomb sandwich structures. Here, coupling loss factors estimation of aluminum honeycomb sandwich structures was studied using the dual formulation method/finite element method (DFM/FEM). The numerical simulation results demonstrated that the proposed method is feasible and effective. The vibration tests on L-shaped aluminum honeycomb sandwich plates were conducted, and the power input method was used to identify the coupling loss factor among the tested plates. The results with the power input method agreed well with those using DFM/FEM. So, the coupling loss factors estimation of aluminum honeycomb sandwich structures using DFM/FEM was verified to be feasible. The method extended applications of SEA in complex structures.

Key words:statistical energy analysis (SEA); dual formulation method (DFM); coupling loss factor; aluminum honeycomb sandwich plates

第一作者 孔宪仁 男，博士，教授，博士生导师，1961年生