局部波动特征分解及其在滚动轴承故障诊断中的应用研究

张　亢， 石阳春, 唐明珠, 吴家腾

(长沙理工大学 能源与动力工程学院，长沙　410076)



局部波动特征分解及其在滚动轴承故障诊断中的应用研究

张亢， 石阳春, 唐明珠, 吴家腾

(长沙理工大学 能源与动力工程学院，长沙410076)

摘要：提出了一种新的自适应时频分析方法——局部波动特征分解(Local Oscillatory-Characteristic Decomposition，LOD)，该方法以信号本身的局部波动特征为基础，并采用微分、坐标域变换、分段线性变换等运算手段将信号分解为一系列瞬时频率具有物理意义的单一波动分量(Mono-Oscillatory Component，MOC)，非常适合于处理多分量信号。在详细说明LOD分解原理的基础上，通过仿真信号将LOD、经验模态分解(Empirical Mode Decomposition，EMD)和局部均值分解(Local Mean Decomposition，LMD)进行了对比分析，结果表明了LOD 的优越性。同时，针对滚动轴承故障振动信号的多分量调制特点，将LOD应用于滚动轴承故障诊断，对滚动轴承实验信号进行了分析，结果表明LOD可以有效地提取滚动轴承故障振动信号的特征。

关键词：非平稳信号；局部波动特征分解；单一波动分量；滚动轴承；故障诊断

滚动轴承故障诊断的关键是从滚动轴承振动信号中提取故障特征，而当滚动轴承发生故障时，其振动信号大多是非平稳、非线性的时变信号，由于时频分析方法能同时提供非平稳信号在时域和频域的局部化信息而在滚动轴承故障诊断中得到了广泛的应用[1-2]。典型的时频分析方法有窗口傅里叶变换、Wigner分布、小波变换等，这些方法有一个共同的缺陷就是缺乏自适应性[3]。由Huang等[3]提出的经验模态分解(Empirical Mode Decomposition，EMD)是一种自适应时频分析方法。它不需要任何的先验知识，而是完全以信号本身的时间尺度特征为基础，将信号分解为若干个固有模态函数(Intrinsic Mode Function，IMF)，然后对每个IMF分量进行Hilbert变换求出瞬时频率和瞬时幅值，即可得到原始信号完整的时频分布。EMD为自适应时频分析提供了一条崭新的思路，是一种真正意义上的自适应时频分析方法，自提出后在机械故障诊断等很多领域都得到了较好的应用[4-7]，但其在理论上还存在一些问题，如过包络、欠包络[8]、模态混淆[9]、端点效应[10]、利用Hilbert变换计算瞬时频率时产生无法解释的负频率[11]、无快速算法而导致计算量大等问题，这些问题仍然处在研究当中。局部均值分解(Local Mean Decomposition，LMD)是由Smith[11]提出的另一种较新的自适应时频分析方法，该方法可以自适应地将一个复杂的多分量信号分解为若干个瞬时频率具有物理意义的乘积函数(Product Function，PF)，其中每一个PF分量由一个包络信号和一个纯调频信号相乘得到，包络信号就是该PF分量的瞬时幅值，而PF分量的瞬时频率则可由纯调频信号直接求出，将所有PF分量的瞬时频率和瞬时幅值组合，便可以得到原始信号完整的时频分布。与EMD 相比，LMD避免了EMD中采用三次样条线形成上、下包络线时产生的过包络、欠包络以及Hilbert变换带来的负频率等问题，并由于其较好的分析多分量调制信号的特点在机械故障诊断领域得到了比较多的应用[12-16]，然而LMD也存在端点效应、模态混淆、解调导致信号突变、计算量大等问题[17-18]，尤其是计算量大的问题，LMD比EMD表现得更为突出。

在借鉴EMD和LMD的自适应时频分析思路的基础上，提出了一种新的自适应时频分析方法——局部波动特征分解(Local Oscillatory-Characteristic Decomposition，LOD)，该方法具体运用了微分、坐标域变换和分段线性变换等运算手段，能够自适应地、快速地将一个复杂信号分解为一系列单一波动分量(Mono-Oscillatory Component，MOC)之和，在理论上具有算法简单、计算效率高、实时性强的特点，适合于对具有非平稳、多分量特点的滚动轴承故障振动信号进行实时分析。本文在提出LOD方法的基础上，通过仿真信号将LOD与EMD、LMD进行了对比分析，结果表明LOD在运算时间、端点效应等方面要优于EMD和LMD，更加适合于实时在线分析；另外，针对滚动轴承故障振动信号的特点，将LOD应用于滚动轴承的故障诊断，对实验信号的分析结果表明，该方法可以有效地应用于滚动轴承的故障诊断。

1局部波动特征分解

LOD沿用了EMD和LMD的基本思路，即根据信号本身的局部波动特征对信号进行自适应分解，得到一系列瞬时频率具有物理意义的单分量信号。具体的LOD算法包含了三种基本运算：① 微分运算。即对原始信号进行微分，然后从微分信号获得原信号的初始均值函数，由于微分能够放大信号的局部波动特征，从而可以使分解结果能更加真实地反映原信号的局部波动特征；② 坐标域变换运算。即将原始信号的坐标通过预先定义的变换式从原数据域变换到锯齿域，继而在锯齿域进行每一步迭代，由于在锯齿域改变了信号不同位置的数据点的稀疏程度，从而可以减小算法的分解误差；③ 分段线性变换运算。即以相邻极值点之间的数据为一段对原信号进行分段线性变换，同时以分段线性变换计算均值曲线，这样大大提高了LOD算法的计算效率与实时处理性。采用LOD自适应地将一个信号分解为若干个分量信号，因为每个分量信号理论上代表了一种波动形式，所以在该方法中将其称为单一波动分量MOC。LOD的具体分解步骤如下：

(1) 找到信号x(t)的所有极值Xk，k=1,2,…,M及其相对应的时刻值τk，k=1,2,…,M。在任意两个相邻极值点[Xk,Xk+1)之间对x(t)进行线性变换，得到分段线性函数s1(t)，线性变换式为：

k=1,2,…M-1

(1)

为了减小算法的分解误差，定义锯齿变换函数，将原数据域坐标(t,x)转换成锯齿域坐标(u,s)，转换公式为：

t∈[τk,τk+1)k=1,2,…M-1

(2)

s(u)=x(t)

(3)

图1　信号坐标变换示意图(实线：数据域信号x(t)，虚线：锯齿域信号s(u))Fig.1 Schematic diagram of the signal coordinates transformation (solid line: data domain signal x(t), dotted line: sawtooth domain signal s(u))

图1为某信号的坐标变换示意图，图中实线为原数据域曲线，实心点为其采样点；虚线为锯齿域曲线，空心点为其采样点。从图中可以看出变换式(2)和(3)并没有改变信号的幅值(纵坐标)，只是对时间轴(横坐标)进行了压缩和扩展，实际效果是：在不改变信号数据点数量的情况下，增大了信号极值点附近的数据点密度，而减小了信号其它位置的数据点密度。对于以信号极值点信息为分解基础的方法，如EMD、LMD等来说，提高信号数据点密度可以获得更高的分解精度[19-21]，而这通常以提高采样频率或数据插值等全局方式来实现，必然导致算法运行时间和空间的增加。利用本文提出的坐标变换，通过对时间轴的压缩和扩展，在不影响算法运行时间与空间的情况下，加大了极值点处数据点密度，从而能获得极值点处更加精确的信息，提高分解精度。

(2) 对x(t)求微分得到x′(t)，找到x′(t)的极值所对应的时刻值τk′，k=1,2,…N，并找出原始信号x(t)中对应于时刻值τk′的函数值Xk′，k=1,2,…N，然后在锯齿域利用线性变换将Xk′，k=1,2,…N线性连接得到m1(u)，m1(u)实际上就是均值函数(即低频分量)，线性变换式如下：

k=1,2,…N-1

(4)

引入微分运算的说明：假设某信号x(t)由两种成分组成，表达如下：

x(t)=A1sin(2πf1t)+A2sin(2πf2t)

(5)

对x(t)进行微分运算后得：

x′(t)=2πf1A1cos(2πf1t)+2πf2A2cos(2πf2t)

(6)

(3) 将原始信号的锯齿域函数s1(u)减去锯齿域均值函数m1(u)，得到c1(u)，c1(u)为一高频函数

c1(u)=s1(u)-m1(u)

(7)

(4) 利用反变换将c1(u)的坐标从锯齿域还原到原数据域c1(t)，即

k=1,2,…N-1

(8)

k=1,2,…N-1

(9)

理想地，如果c1(t)为一个瞬时频率具有物理意义的单分量信号，则c1(t)为x(t)的第1个MOC分量MOC1(t)；

(5) 如果c1(t)不是一个瞬时频率具有物理意义的单分量信号，则将c1(t)作为原始信号重复步骤(1)～(4)，循环m次，直至得到瞬时频率具有物理意义的单分量信号cm(t)，cm(t)即为信号x(t)的第一个分量MOC1(t)。

从上述迭代分解过程可以看出，LOD是基于信号本身的局部波动特征的，即是自适应的，另外LOD是基于线性变换的，且每次线性变换只需任意两个相邻极值点之间的信息，无需整个原始数据的信息，因此，LOD算法计算效率高，具有较强的实时处理性。而对于LOD的分解结果MOC分量，由于分解过程中不但保证了相邻极值点间的单调性，且迭代过程中采用了减去均值曲线的方式，也就保证了其包络的局部对称性，因此，理论上MOC分量是满足瞬时频率具有物理意义的条件的[3,11]。

2仿真信号分析

首先考察由三个正弦分量组成的仿真信号x(t)，表达式如式(10)所示。

x(t)=sin(60πt)+sin(6πt)+sin(πt)

t∈[0,5]

(10)

与EMD一样，LOD也是以信号局部极值点为基础的，因此也存在端点效应现象。为了和EMD进行对比，首先在不对端点进行处理的情况下，分别采用LOD和EMD对仿真信号x(t)进行分析。

不处理端点情况下，x(t)的LOD分解结果如图2所示，共得到了3个MOC分量和1个余量，可以看出，3个MOC分量虽然受到了端点效应的影响，但仍较好地对应了仿真信号x(t)的3个组成分量，说明了LOD的自适应分解特性。分解过程中采用标准差(Standard Deviation，SD)判据[3]作为迭代终止条件，即通过计算连续两次迭代结果的标准差值，并与预先确定的阈值进行比较，以此决定迭代的终止点，本次分解设定SD<0.3。

图2　仿真信号的LOD分解结果(未处理端点)Fig.2 Decomposition results of the LOD (unprocessed endpoints)

同样在不处理端点的情况下采用EMD对x(t)进行分解，结果如图3所示，共得到了8个IMF分量和1个余量。其中，前两个IMF分量c1(t)和c2(t)，虽然分别对应了x(t)中30 Hz和3 Hz分量，但与LOD的分解结果比较，其端点效应要严重一些。其余IMF分量，幅值明显偏大，且找不到与x(t)中的0.5 Hz分量对应的IMF分量，说明全是虚假成分。造成此现象的原因是在EMD分解中，采用的是三次样条函数对极值点插值形成上、下包络线，而以上包络线为例，每对1个极大值点进行三次样条插值，就要用到其本身及左、右相邻各1个极大值点的信息，如果将信号端点作为一个极大值点，那么端点效应至少会波及到信号端点附近的3个极大值点，下包络线同理。于是，对于x(t)中的0.5 Hz分量，由于只包含了3个极大值点和2个极小值点，因此如果不对x(t)进行延拓，那么左、右两端的端点效应，将会波及整个信号，这便造成了0.5 Hz分量的完全失真，即无法分解出0.5 Hz分量。而在LOD分解中采用了分段线性变换方式，每一段只需相邻两个极值点的信息，且不区分极大值点和极小值点。因此，如果将信号端点作为一个极值点，那么端点效应只会波及到信号端点附近的两个极值点。于是，对于LOD即便没有进行端点处理，也能够分解出0.5 Hz的分量。以上说明，在未对端点进行处理的情况下，LOD受端点效应的影响没有EMD严重。

图3　仿真信号的EMD分解结果(未处理端点)Fig.3 Decomposition results of the EMD (unprocessed endpoints)

利用自适应波形匹配延拓法[22]对仿真信号x(t)进行延拓后，采用LOD和EMD分解，结果分别如图4和图5所示。从图4可以看出，LOD的分解效果非常好，余量的幅值相比未延拓时也有所减小；从图5的EMD分解结果可以看出，各个IMF分量很好地对应了仿真信号的组成分量，端点效应得到了明显改善，且由于延拓后增加了极值点数目，从而分解出了0.5 Hz的分量，也验证了前述的解释。对比图4和图5可以看出，LOD分解的余量幅值要小于EMD的，说明LOD分解的整体效果要优于EMD。

图4　仿真信号的LOD分解结果(已处理端点)Fig.4 Decomposition results of the LOD (processed endpoints)

图5　仿真信号的EMD分解结果(已处理端点)Fig.5 Decomposition results of the EMD (processed endpoints)

进一步考察含有调制分量的仿真信号x(t)，x(t)的表达式如式(11)所示。

x(t)=3exp(-0.5t)sin(2πt)+

5sin(20πt)+10sin(60πt)

t∈[0,5]

(11)

图6　仿真信号x(t)的LOD分解结果Fig.6 The decomposition results of LOD about simulation signal x(t)

图7　仿真信号x(t)的EMD分解结果Fig.7 The decomposition results of EMD about simulation signal x(t)

图8　仿真信号x(t)的LMD分解结果Fig.8 The decomposition results of LMD about simulation signal x(t)

3在滚动轴承故障诊断中的应用

当滚动轴承发生故障时，其振动信号通常是包含噪声的多分量信号，要提取故障特征，就需要对其进行分解与降噪。由于LOD的本质是将多分量信号自适应地分解为若干个单分量信号，因此本文首先采用LOD将滚动轴承故障振动信号分解为若干个MOC分量，然后利用Hilbert变换对包含故障信息的MOC分量进行包络分析，得到Hilbert包络谱，从而提取滚动轴承故障振动信号的故障特征。

为了验证该方法，在旋转机械故障实验台上进行了实验。滚动轴承的局部损伤可能发生在外圈、内圈和滚动体上，本文分别用两个6311型的球轴承进行了实验，两个轴承分别被设置有内圈和外圈局部故障，由于实验条件的限制未能在滚动体上设置故障。故障是通过激光切割在内圈或外圈上开槽来设置的，槽宽为0.15 mm，槽深为0.13 mm，设置的故障程度属较轻微的程度。将加速度传感器安装在轴承座上，用来采集滚动轴承的振动加速度信号。

图9是测得的外圈有凹槽的滚动轴承振动加速度信号的时域波形，信号采样频率为4 096 Hz，转频fr为25 Hz，经计算外圈故障特征频率为fo=76 Hz。

图9　滚动轴承外圈故障振动加速度信号时域波形Fig.9 The time domain waveform of the vibration acceleration signal about rolling bearing outer ring fault

采用LOD对该信号进行分解，共得到11个MOC分量和一个余量，其中前4个MOC分量如图10所示，可以看出每个MOC分量都表征了原始信号的一种时间尺度特征。由于滚动轴承的故障特征一般包含在高频段，因此进一步对分量MOC1(t)进行Hilbert包络谱分析，结果如图11所示。从图11中可以清楚地看出，在外圈故障特征频率76 Hz处及其2倍频152 Hz处存在明显的谱线，另外还存在转频及其倍频成分，可以判定滚动轴承存在外圈局部故障，与实际情况相符。

图10　滚动轴承外圈故障振动加速度信号的LOD分解结果Fig.10 The decomposition results of LOD about rolling bearing outer ring fault signal

图11　第1个MOC分量的Hilbert包络谱Fig.11 The Hilbert envelope spectrum of the first MOC

将LOD改为LMD，以同样的步骤对该外圈故障信号进行分析。LMD分解的前4个分量和第一个PF分量PF1(t)的Hilbert包络谱分别如图12和图13所示，对比图10和图11可以看出，LMD与LOD的整体分解效果是一致的，且PF1(t)的Hilbert包络谱和MOC1(t)的Hilbert包络谱包含的主要频率成分也是一样的，同样能判断出滚动轴承的状态。但在PF1(t)的0.108 s处存在失真，另外，LOD分解得到前4个分量的时间tlod=0.033 7 s，LMD分解得到前4个分量的时间tlmd=0.104 3 s，在计算效率上LOD也优于LMD。

图14是内圈有凹槽的滚动轴承振动加速度信号的时域波形，信号采样频率为4 096 Hz，转频fr为20 Hz，经计算内圈故障特征频率为fi=99.2 Hz。采用LOD方法对该振动加速度信号进行分解，得到13个MOC分量和1个余量，其中前4个MOC分量如图15所示。同样，对第1个MOC分量进行Hilbert包络谱分析，结果如图16所示。从图16中可以看出在内圈故障特征频率99.2 Hz处，以及2倍、3倍转频处存在明显的谱线，这符合滚动轴承内圈故障的特征，说明了该方法能有效地诊断出滚动轴承存在内圈故障。

图12　滚动轴承外圈故障振动加速度信号的LMD分解结果Fig.12 The decomposition results of LMD about rolling bearing outer ring fault signal

图13　第1个PF分量的Hilbert包络谱Fig.13 The Hilbert envelope spectrum of the first PF

图14　滚动轴承内圈故障振动加速度信号时域波形Fig.14 The time domain waveform of the vibration acceleration signal about rolling bearing inner ring fault

图15　滚动轴承内圈故障振动加速度信号的LOD分解结果Fig.15 The decomposition results of LOD about rolling bearing inner ring fault signal

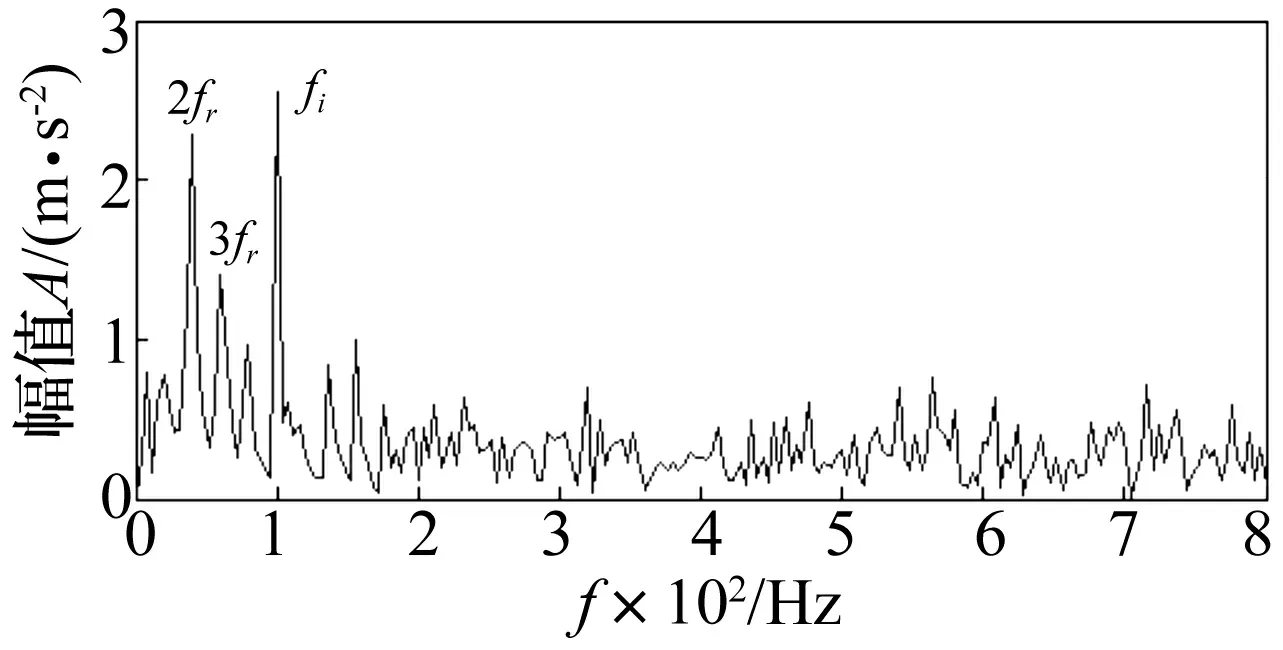
图16　第1个MOC分量的Hilbert包络谱Fig.16 The Hilbert envelope spectrum of the first MOC

4结论

根据EMD和LMD的自适应时频分析思想，提出了一种新的非平稳信号分析方法——局部波动特征分解，通过仿真信号将LOD与EMD、LMD进行了对比分析，同时将LOD应用于滚动轴承故障诊断，得出了以下结论：

(1) LOD算法效率高，分解时间短。在LOD算法中采用了分段线性变换的方式，即每次只需知道信号任意两个相邻极值点之间的信息，所以在同一时刻，可以并行处理不同“段”的信号，而EMD必须知道信号所有的信息后才能进行处理；另外，LOD通过线性变换获得均值函数，避免了EMD采用三次样条线形成上、下包络线，以包络平均线作为均值函数，以及LMD中通过不断平滑的方式获得均值函数的方式，这样大大减少了计算量。因此，相比于EMD和LMD，LOD具有更高的计算效率，更有利于信号的实时在线分析。

(2) LOD方法的端点效应不明显。LOD采用分段的方式，端点效应只会波及信号端点至相邻极值点部分，且迭代次数少，因而端点效应不明显。而EMD的端点效应会波及到信号端点附近多个极值点，且迭代次数较多，因而端点效应较明显。

(3) 针对滚动轴承故障振动信号的多分量调制特点，采用LOD对滚动轴承实验信号进行了分析，结果表明基于LOD的Hilbert包络谱可以有效地提取滚动轴承故障振动信号的故障特征，说明LOD可以用于滚动轴承的故障诊断。

LOD方法拥有一些优点，但作为一种新提出的方法，还有一些理论问题需要研究和完善，如迭代终止条件的选择、MOC的单分量性质的严格证明、LOD的分解能力等。随着这些问题的深入研究，LOD方法将得到更广泛的应用。

参 考 文 献

[1] Rafiee J, Tse P W. Use of autocorrelation of wavelet coefficients for fault diagnosis[J]. Mechanical Systems and Signal Processing, 2009, 23(5): 1554-1572.

[2] Wu J D, Chiang P H. Application of Wigner-Ville distribution and probability neural network for scooter engine fault diagnosis[J]. Expert Systems with Applications, 2009, 36(2): 2187-2199.

[3] Huang N E, Shen Z, Long S R. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A, 1998, 454: 903-995.

[4] Wu Fang-ji, Qu Liang-sheng. Diagnosis of subharmonic faults of large rotating machinery based on EMD[J]. Mechanical Systems and Signal Processing, 2009, 23(2): 467-475.

[5] Cheng Jun-sheng, Yu De-jie, Yang Yu. Application of SVM and SVD technique based on EMD to the fault diagnosis of the rotating machinery[J]. Shock and Vibration, 2009, 16(1): 89-98.

[6] He X H, Hua X G, Chen Z Q, et al. EMD-based random decrement technique for modal parameter identification of an existing railway bridge[J]. Engineering Structures, 2011, 33(4):1348-1356.

[7] Shiau Y H, Wu M C. Detecting characteristics of information masked by a laser-triggered microwave system via Hilbert-Huang transform[J]. Optics Communications, 2010,283(9): 1909-1916.

[8] Pegram G G S, Peel M C, McMahon T A. Empirical mode decomposition using rational splines: an application to rainfall time series[J]. Proceedings of the Royal Society A, 2008, 464: 1483-1501.

[9] Wu Zhao-hua，Huang N E. A study of the characteristics of white noise using the empirical mode decomposition method[J]. Proc. R. Soc. Lond. A，2004，460(3): 1597-1611.

[10] Wu Fang-ji, Qu Liang-sheng. An improved method for restraining the end effect in empirical mode decomposition and its applications to the fault diagnosis of large rotating machinery[J]. Journal of Sound and Vibration,2008,314(3/4/5): 586-602.

[11] Smith J S. The local mean decomposition and its application to EEG perception data[J]. Journal of the Royal Society Interface, 2005, 2(5): 443-454.

[12] 程军圣, 杨宇, 于德介. 局部均值分解方法及其在齿轮故障诊断中的应用[J]. 振动工程学报, 2009, 22(1): 76-84.

CHENG Jun-sheng, YANG Yu, YU De-jie, The local mean decomposition method and its application to gear fault diagnosis[J]. Journal of Vibration Engineering, 2009,22(1): 76-84.

[13] 李慧梅, 安钢, 黄梦. 基于局部均值分解的边际谱在滚动轴承故障诊断中的应用[J]. 振动与冲击, 2014, 33(3): 5-8.

LI Hui-mei, AN Gang, HUANG Meng. Application of marginal spectrum based on local mean decomposition in rolling bearing fault diagnosis[J]. Journal of Vibration and Shock, 2014, 33(3): 5-8.

[14] Wang Yan-xue, He Zheng-jia, Zi Yan-yang. A demodulation method based on local mean decomposition and its application in rub-impact fault diagnosis[J]. Measurement Science and Technology, 2009, 20(2): 1-10.

[15] Wang Yan-xue, He Zheng-jia, Zi Yan-yang. A comparative study on the local mean decomposition and empirical mode decomposition and their applications to rotating machinery health diagnosis[J]. Journal of Vibration and Acoustics, 2010, 132(2): 1-10.

[16] Cheng Jun-sheng, Yang Yi, Yang Yu. A rotating machinery fault diagnosis method based on local mean decomposition[J]. Digital Signal Processing, 2012, 22(2): 356-366.

[17] 任达千. 基于局域均值分解的旋转机械故障特征提取方法及系统研究[D]. 杭州: 浙江大学, 2008.

[18] 张亢. 局部均值分解方法及其在旋转机械故障诊断中的应用研究[D]. 长沙: 湖南大学, 2012.

[19] Rilling G, Flandrin P. Sampling effects on the empirical mode decomposition[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 43-59.

[20] Rilling G, Flandrin P, Goncalves P. On empirical mode decomposition and its algorithms[C]. Ieee-eurasip Workshop on Nonlinear Signal and Image Processing, Grado, June, 2003: 8-11.

[21] 胡维平, 杜明辉. 信号采样率对经验模态分解的影响研究[J]. 信号处理, 2007, 23(4): 637-640.

HU Wei-ping, DU Ming-hui. The limitation of sampling for the empirical mode decomposition[J]. Signal Processing, 2007, 23(4): 637-640.

[22] 张亢, 程军圣, 杨宇. 基于自适应波形匹配延拓的局部均值分解端点效应处理方法[J]. 中国机械工程, 2010, 21(4): 457-462.

ZHANG Kang, CHENG Jun-sheng, YANG Yu. Processing method for end effects of local mean decomposition based on self-adaptive waveform matching extending[J]. China Mechanical Engineering, 2010, 21(4): 457-462.

基金项目：国家自然科学基金(51305046)；湖南省科技计划项目(2013FJ6015)；湖南省教育厅一般项目(12A00714C0025)

收稿日期：2014-09-23修改稿收到日期：2014-12-03

中图分类号:TN911.7;TH165.3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.01.016

Local oscillatory-characteristic decomposition and its application in roller bearing fault diagnosis

ZHANG Kang, SHI Yang-chun, TANG Ming-zhu, WU Jia-teng

(School of Energy and Power Engineering, Changsha University of Science and Technology, Changsha 410076, China)

Abstract:A new self-adaptive time-frequency analysis method named local oscillatory-characteristic decomposition (LOD) was proposed. This method was based on local oscillatory characteristics of a signal itself, the operations including differential, coordinates domain transform and piecewise linear transform were used to decompose the signal into a series of mono-oscillatory components (MOC), their instantaneous frequency had physical meanings, and thus they were suitable for processing multi-component signals. After illustrating the decomposition principle of LOD in detail, the LOD was compared with the empirical mode decomposition (EMD) method and the local mean decomposition (LMD) method by analyzing simulated signals. The results showed that the LOD method is superior to the other two. Meanwhile, aiming at the multi-component modulated feature of roller bearing fault vibration signals, the LOD was applied in roller bearing fault diagnosis. The results demonstrated that the LOD can extract fault characteristics in roller bearing fault vibration signals effectively.

Key words:nonstationary signal; local oscillatory-characteristic decomposition; mono-oscillatory component; roller bearing; fault diagnosis

第一作者 张亢 男，博士，讲师，1983年11月生