冲击振动提取的优化稀疏表征方法

秦　毅, 郭　磊, 吴宏钢

(1.重庆大学 机械传动国家重点实验室，重庆　400044; 2. 重庆通信学院,重庆　400035)



冲击振动提取的优化稀疏表征方法

秦毅1, 郭磊1, 吴宏钢2

(1.重庆大学 机械传动国家重点实验室，重庆400044; 2. 重庆通信学院,重庆400035)

摘要：针对在背景噪声及其他振动干扰下冲击振动信号提取问题，提出了一种利用基追踪实现冲击振动优化稀疏表征的方法。建立了冲击振动提取的稀疏求解问题模型，设计了用于冲击振动特征提取的变换基，并利用特征谱线在频谱中所占能量比作为评价冲击振动提取效果的指标，实现了冲击振动成分的优化提取。将该方法用于仿真试验和齿轮故障诊断，结果表明，与Morlet小波软阈值方法相比，所提方法能更好地提取微弱周期性冲击成分，具有很好的应用前景。

关键词：稀疏求解；基追踪；变换基；齿轮故障；特征提取

振动信号是机械设备在运行过程中的动力学外在表现形式，包含了丰富的状态信息，对其分析处理是机械设备状态监测和故障诊断的有效途径。对于旋转机械而言，在众多的故障特征中，冲击故障又占据了较高的比例。例如，当滚动轴承或齿轮出现故障时，损伤点与其他部位的周期性碰撞会引发周期性冲击振动信号。但由于复杂的机械设备和工作环境，冲击振动常常淹没在工频振动、谐波振动和背景噪声中。因此，研究如何提取冲击振动的发生时刻和振荡频率对旋转机械故障诊断意义重大。

针对冲击故障振动的非平稳性，学者们提出了时频分析、小波变换、谱峭度滤波、经验模态分解(EMD)等多种方法来提取冲击特征[1-4]。Morlet小波[5]和Laplace小波[6]常被用于提取冲击响应成分，并通过引入小波熵来优化小波基。李昌林等[7]将EEMD与Laplace小波相结合来提取多阶模态的冲击响应。梁霖等[8]利用非线性流形学习方法来提取冲击故障特征。李允公等[9]提出了周期序列变换来识别周期性冲击响应成分。以上方法在低噪声的情况下，能准确检测出信号中的冲击振动分量，但在噪声较强的情况下，噪声会对这些方法的有效性和检测精度带来很大干扰，因此有必要研究一种能在强噪声背景下准确提取冲击振动分量的方法。

稀疏表征通过使用合适的基函数来最简化表征信号，可以用于特征振动分量的提取。于是，本文提出基于稀疏求解的冲击振动优化提取方法，以解决在较强背景噪声中冲击特征的准确识别问题。通过对仿真信号和齿轮故障振动信号进行试验的结果验证了该方法的有效性和先进性。

1信号稀疏求解问题

在信号分析中，通常希望将信号表示为多个特征向量的线性组合。而信号稀疏表征就是指找到一种简洁的方式来表示信号，使得绝大部分变换系数的值接近于零或等于零，从而使得到的变换信号是稀疏或者近似稀疏的。

对于某一个信号，均可以用以下欠定方程(1)进行表示：

y=Ax

(1)

式中:A为M×N的变换矩阵，y为长度为M的向量，x为长度为N的向量，且N>M。显然，该系统未知量的个数多于方程的个数，同时矩阵A的宽度大于其长度，当假定AA*可逆时，则方程组有无穷解。因此，通常采用最小二乘法来求解该方程。为更好地表征信号，可以采用基追踪方法(BP)。首先介绍范数l1和l2，其定义分别为式(2)和(3)所示：

(2)

(3)

于是可以通过使x的绝对值之和最小来求解式(1)，即求解以下优化问题。

(4)

式(4)也即是著名的基追踪(BP)问题。

对于传统的最小二乘法，它是求取的平方和的最小值，相比求取绝对值的和最小值，其对信号中的较大值更加敏感，如图1所示。因此，当采用最小二乘法时，为保证平方和最小，需要取得少量的较大值，因为相比于小值，它们的影响更大，这样，最后求取的信号中有更多的小值，也就造成了信号的不稀疏。相反，基于基追踪降噪(BPD)的方法就不会包含很多较小值，从而会获得更加稀疏的信号。

2冲击特征的稀疏提取

由于机械设备的复杂性以及振动传递路径的影响，从传感器拾取的滚动轴承或齿轮振动信号不仅包括冲击振动，而且包括噪声和其他一些振动成分，如噪声、部件本身的固有振动、加工误差引起的振动等。于是，被测含有冲击特征的振动信号y(n)可表示为

y(n)=x(n)+w(n)

(5)

式中:x(n)表示冲击振动，w(n)表示噪声和其他振动。通过选取合适的变换基A可以对冲击振动x(n)进行稀疏表征，于是y(n)可重新表达为如下形式：

Y=Ac+w

(6)

式中:A代表变换基矩阵，c代表变换系数，Y代表含有冲击特征的振动信号，w代表噪声和其他振动。变换系数c可以通过基追踪方法来计算，即求解以下问题：

(7)

为了提取冲击故障，如何选取或设计相应的变换基是需要解决的一个关键问题。首先假定用脉冲函数表示一个冲击

p(t)=δ(t)

(8)

易知，其傅里叶变换为

P(f)=1

(9)

若取变换基矩阵A可以取为单位矩阵，即

A(i,j)=1

(10)

式中:i=1,2,…,N，j=1,2,…,N，N表示信号长度。由傅里叶反变换可知，可用变换矩阵中任一列向量表示相应时刻的冲击，即可用A中第j列向量来表征第j个时间点处的冲击信号。因此，利用式(10)所示的变换基可以有效地提取到信号中所有时刻的冲击成分。需要注意的是，虽然工程中的冲击信号不是理想的脉冲函数，但仍能用脉冲函数进行近似表示。

3冲击振动的优化表征方法

3.1稀疏求解算法

本文需要解决的问题式(7)实际上属于凸优化问题，可以采用迭代阈值收缩算法(ISTA)、Split Bregman迭代算法和“分离变量的增广拉格朗日收敛算法”(SALSA)进行求解[10]。其中，ISTA和Split Bregman迭代算法能够保证在每次迭代后成本函数值的减小，但是它们具有收敛慢的缺点；而SALSA采用了分离变量和最小二乘求解方法，具有很好的收敛性和较快的计算速度。因此，本文采用SALSA算法来求解式(7)。

首先，在RN上定义两个凸能量函数f1(x)和f2(x)，其中x为自变量，给出极小化模型：

(11)

为分离变量，引入中间变量v，并将v作为函数f2的自变量，这样上式就转化为以下约束问题：

s.t.x=v

(12)

显然，该问题等价于问题式(11)。然后，利用以下增广型拉格朗日模型求解：

L(x,λ,μ)=f1(x)+f2(v)+

(13)

式中:λ为拉格朗日乘数，μ≥0为惩罚参数。对于该增广型拉格朗日模型，可以引入序列dk，进行迭代，从而达到不断收敛的效果，迭代算法过程如下：

(xk+1,vk+1)∈argminf1(x)+f2(v)+

(14)

dk+1=dk-(xk+1-vk+1)

(15)

易知，式(7)能够表示为式(11)，因此可以用SALSA算法求解式(7)。

3.2参数优化

在式(7)给出的优化问题中，参数λ的选取对于冲击特征提取效果具有重要的影响。经过试验发现，若选择较大的λ，不仅干扰信号大大衰减，而且冲击振动也大大衰减；而若选择较小的λ，冲击振动可能仍然淹没在其他干扰信号中。因此，可以通过选取合适的指标函数，利用优化方法确定合适的λ，以获得最好的冲击特征提取效果。

为确定评价指标，首先考察周期冲击振动信号波形及其频谱。周期冲击振动信号通常可定义为

式中:ξ=226.2，ωd=1 440π，Ak=1，T=0.6和t∈[0,4]。ξ主要是控制冲击的支撑区间，即ξ越大衰减越快。假定采样频率为1 500 Hz，则该周期冲击振动信号的时域波形和频谱分别如图1(a)和(b)所示。从图1(b)可见，周期冲击振动信号的频谱是以冲击频率fp(fp=1/T)为周期的一系列谱线，其中冲击频率的一倍频和二倍频出谱线较大。因此，可以选择这两根谱线在频谱中所占能量比作为评价冲击振动提取效果的指标。评价指标可定义为

(17)

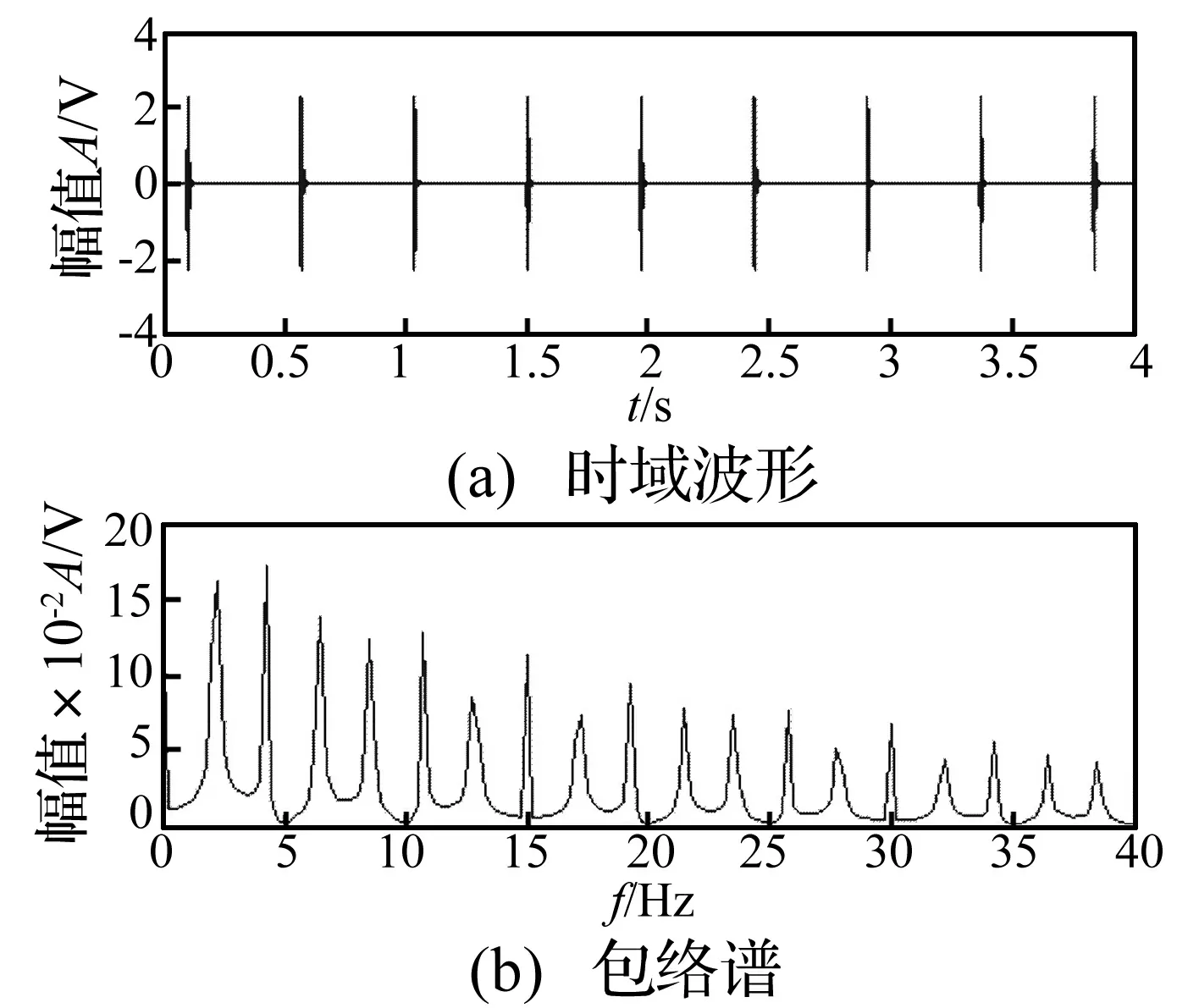
图1　周期冲击振动信号的时域波形和包络谱Fig.1 The waveform and envelope spectrum of theperiodic impact vibration signal

式中:H(f)为h(t)的频谱。从式(17)可以看出，若提取结果中还存在噪声或谐波振动时，式(17)的分母会增大，从而使e减小，并且随着噪声或谐波振动能量的增加，评价指标e会越来越小；另外，若冲击振动的峰值减小，式(17)的分子会相对于分母减小更多，从而导致e减小。因此，该评价指标可以衡量提取结果中冲击振动成分的大小。需要注意的是，由于冲击频率未知，可以采用多次试验统计的方法来初步确定fp。

综合以上分析，本文提出的冲击特征优化提取算法如下：

(1) 依次为λ取多个值，如λ=5,6,…,20，然后分别通过式(7)提取冲击振动，计算各冲击振动的包络谱，统计最大峰值频率和次最大峰值频率的出现次数，从中找到出现次数最多的两个频率，取其中值较小的为特征频率fp。

(2) 设定λ的搜索范围(如λ∈[1,20])及搜索步长(可取为0.5或1)。

(3) 分别在给定的λ下，提取冲击振动，计算其包络谱，然后按式(17)计算与各个λ对应的评价指标。

(4) 获得与最大e对应的参数λ，利用SALSA算法求解式(7)，得到优化的冲击振动提取结果。

4仿真分析

下面通过两个具有不同噪声的仿真信号对本文所提出方法的有效性进行验证。

首先取一含有工频振动、谐波振动、冲击振动和低噪声的仿真信号

s(t)=cos(2π×175t)+0.8cos(2π×350t)+

0.6cos(2π×700t)+h(t)+n(t)

(18)

式中:h(t)由式(16)定义，n(t)是标准差为0.1的白噪声。假定采样频率仍为1 500 Hz，则该仿真信号的时域波形如图2所示。利用本文所提出的方法去提取冲击振动，所得冲击振动信号及其包络谱分别如图3和4所示。在图3中，我们可以清楚地看到冲击振动的时间间隔T等于0.467 s，而从它的包络谱中可以知道冲击频率为2.143 Hz。可见，本文方法能有效地检测出冲击振动信号。评价指标e与参数λ的关系曲线如图5所示。从图5中可见，通过该评价指标曲线的极大值点容易找到优化的参数λ，此时极大值点对应的λ和e分别为0.1和12.5。

为了检验本文方法在较强噪声背景下的性能，取噪声更大的仿真信号进行试验。于是，本文将式(18)中的n(t)变成标准差为0.35的白噪声，则仿真信号的时域波形如图6所示。比较图2和图6可见，此时的冲击信号已被噪声所淹没，已经很难判断信号中是否有冲击成分。因此，可以利用本文方法去提取冲击成分，所得结果如图7所示。图中T表示冲击间隔。此时的最优参数λ及其对应的评价指标e分别为0.01和18。从图7中可见，本文方法成功从较强背景噪声中提取出冲击振动。该冲击振动的包络谱如图8所示。从图8中可以准确知道冲击频率。另外，为了突出本文方法的优势，将基于小波熵优化的Morlet小波软阈值方法[11]用于对比分析，所得结果及其包络谱分别如图9和10所示。从图9中可见，利用Morlet小波软阈值方法检测的结果受噪声干扰较大，且提取到的明显的等周期冲击个数较少。进一步比较图8和10可知，本文方法所得包络谱在特征频率及其倍频处的谱线更加明显，且等间隔谱线条数越多。因此，本文提出的优化稀疏表征方法的效果优于Morlet小波软阈值方法。

图2 低噪声仿真信号时域波形Fig.2Thewaveformofsimulatedsignalwithlownoise图3 低噪声仿真信号提取结果Fig.3Theextractionresultofsimulatedsignalwithlownoise图4 低噪声仿真信号提取结果的包络谱Fig.4Theenvelopespectrumoftheextractionresultofsimulatedsignalwithlownoise

图5 评价指标e与参数λ的关系曲线Fig.5Therelationcurvebetweenevaluationindexeandparameterλ图6 强噪声仿真信号时域波形Fig.6Thewaveformofsimulatedsignalwithstrongnoise图7 本文方法提取结果Fig.7Theresultobtainedbytheproposedmethod

图8 本文方法提取结果的包络谱Fig.8Theenvelopespectrumofresultobtainedbytheproposedmethod图9 Morlet小波软阈值方法提取结果Fig.9Theresultobtainedbythesoft-thresholdingmethodbasedonMorletwavelet图10 Morlet小波软阈值方法提取结果的包络谱Fig.10Theenvelopespectrumofresultobtainedbythesoft-thresholdingmethodbasedonMorletwavelet

5在机械故障诊断中的应用

当机械设备运转时，若齿轮发生了剥落、点蚀、裂纹等局部损伤故障，会使齿轮在运行过程中发生局部冲击现象，而这些冲击往往包含在它们的振动信号中。于是，从拾取的振动信号中检测这些冲击成分就成为诊断齿轮故障的一个重要技术手段。但齿轮振动故障特征往往受到其他振动和噪声的干扰，因此可以将本文所提方法用于齿轮冲击故障特征提取。

在齿轮故障实验台上进行了相关实验。选取一主动轮发生了裂纹故障的单级齿轮箱进行试验，其中主动轮和从动轮齿数分别为28和36。试验中设定输入轴转速为1 230 r/min，即转频fr为20.5 Hz，然后利用PCB加速度计采集振动信号，其中采样频率为4 096 Hz。采集到的振动波形及其包络谱分别如图11和12所示。从图11中很难看出其中的冲击成分，而从图12中可见，在故障特征频率fr及其二倍频和三倍频处的谱线都不明显。于是利用本文所提方法提取其中的冲击振动。获得的冲击成分波形如图13所示。为了准确获取故障特征，对该冲击信号进行包络谱分析，所得结果如图14所示。从图中可见，在故障特征频率fr及其二倍频、三倍频和四倍频处出现了明显的谱线，这就表明该周期冲击振动信号的冲击频率为fr，因此可以判断主动轮发生了局部故障。

同样地，将基于小波熵优化的Morlet小波软阈值方法用于提取该齿轮故障振动信号中的冲击成分，所得冲击信号波形和其包络谱分别如图15和16所示。比较图13和15可知，本文方法提取的冲击更加明显且受噪声影响较小。再对比图14和16可知，虽然Morlet小波软阈值方法所得包络谱在故障特征频率fr及其二倍频处有较高的谱线，但在三倍频和四倍频处的谱线较低和不明显。因此，本文方法更适于在较强干扰下提取齿轮冲击故障特征。

图11 齿轮故障振动信号波形Fig.11Thewaveformofgearfaultvibrationsignal图12 齿轮故障振动信号包络谱Fig.12Theenvelopespectrumofgearfaultvibrationsignal图13 本文方法提取的齿轮冲击振动信号Fig.13Thegearimpactvibrationobtainedbytheproposedmethod

图14 本文方法提取的齿轮冲击振动信号的包络谱Fig.14Theenvelopespectrumofgearimpactvibrationobtainedbytheproposedmethod图15 Morlet小波软阈值方法提取的齿轮冲击振动信号Fig.15Thegearimpactvibrationobtainedbythesoft-thresholdingmethodbasedonMorletwavelet图16 Morlet小波软阈值方法提取的齿轮冲击振动信号包络谱Fig.16Theenvelopespectrumofgearimpactvibrationobtainedbythesoft-thresholdingmethodbasedonMorletwavelet

6结论

本文首先建立了冲击振动提取的稀疏求解问题模型，构造了用于冲击振动特征提取的变换基，然后利用基追踪方法进行求解。同时，根据参数λ对冲击提取结果的重要性，通过利用特征谱线在频谱中所占能量比作为评价指标，提出了基于SALSA算法的冲击特征优化提取方法。仿真实验和在齿轮故障诊断中的应用结果表明，在较强噪声和其他振动干扰下，本文方法比Morlet小波软阈值方法能更好地提取出冲击特征成分，且诊断效果更好。

参 考 文 献

[1] 崔玲丽, 康晨晖, 胥永刚, 等. 滚动轴承早期冲击性故障特征提取的综合算法研究[J]. 仪器仪表学报, 2010, 31(11): 2422-2427.

CUI Ling-li, KANG Chen-hui, XU Yong-gang, et al. Integrated algorithm research on early impactive fault feature extraction of rolling bearings[J]. Chinese Journal of Scientific Instrument, 2010, 31(11): 2422-2427.

[2] 蔡改改, 刘海洋, 黄伟国, 等. 自适应谱峭度滤波方法及其振动信号检测应用[J]. 振动、测试与诊断, 2014, 34(2): 212-217.

CAI Gai-gai, LIU Hai-yang, HUANG Wei-guo, et al. Adaptive spectral Kurtosis filtering and its application for detection ofvibration signal[J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(2): 212-217.

[3] 蔡艳平，李艾华，石林锁，等. 基于EMD 与谱峭度的滚动轴承故障检测改进包络谱分析[J]. 振动与冲击, 2011, 30(2): 167-172.

CAI Yan-ping, LI Ai-hua, SHI Lin-suo, et al. Roller bearing fault detection using improved envelope spectrum analysis based on EMD and spectrum kurtosis[J]. Journal of Vibration and Shock, 2011, 30(2): 167-172.

[4] QIN Yi, WANG Jia-xu, MAO Yong-fang. Dense framelets with two generators and their application in mechanical fault diagnosis [J]. Mechanical Systems and Signal Processing, 2013, 40(2): 483-498.

[5] 林京, 屈梁生. 基于连续小波变换的信号检测技术与故障诊断[J]. 机械工程学报, 2000, 36(2): 95-100.

LIN Jin, QU Liang-shen. Feature detection and fault diagnosis based on continuous wavelet transform[J]. Chinese Journal of Mechanical Engineering, 2000, 36(2): 95-100.

[6] 祁克玉, 向家伟, 訾艳阳, 等. 基于Laplace小波相关滤波的结构模态参数精确识别方法[J]. 机械工程学报, 2007, 43(9): 167-172.

QI Ke-yu,XIANG Jia-wei, ZI Yan-yang, et al. High precision modal parameter identification based on Laplace wavelet correlation filtering [J]. Chinese Journal of Mechanical Engineering, 2007, 43(9): 167-172.

[7] 李昌林, 孔凡让, 黄伟国, 等. 基于EEMD 和Laplace小波的滚动轴承故障诊断[J]. 振动与冲击, 2014, 33(3): 63-69.

LI Chang-lin, KONG Fan-rang, HUANG Wei-guo, et al.Rolling bearing fault diagnosis based on EEMD and Laplace wavelet[J]. Journal of Vibration and Shock, 2014, 33(3): 63-69.

[8] 梁霖, 徐光华, 栗茂林. 冲击故障特征提取的非线性流形学习方法[J]. 西安交通大学学报, 2009, 43(11): 95-99.

LIANG Lin, XU Guang-hua, LI Mao-lin, et al. Nonlinear manifold learning method of mechanical impact faults extraction[J]. Journal of Xi’an Jiaotong University, 2009, 43(11): 95-99.

[9] 李允公, 刘杰, 张金萍. 基于实测冲击响应的转子碰摩故障特征提取方法[J]. 机械工程学报, 2007, 43(4): 224-228.

LI Yun-gong, LIU Jie, ZHANG Jin-ping. Signature extracting method of the fault of rubbing rotor based on measured impulse response[J]. Chinese Journal of Mechanical Engineering, 2007, 43(4): 224-228.

[10] Afonso M V, Bioucas-dias J M, Figueiredo M A T. An augmented Lagrangian approach to the constrained optimization formulation of imaging inverse problems[J]. IEEE Trans. Image Process, 2011, 20(3): 681-695.

[11] LIN Jin, QU Liang-shen. Feature extraction based on Morlet wavelet and its application for mechanical fault diagnosis[J]. Journal of Sound and Vibration, 2000, 234(1): 135-148.

基金项目：国家自然科学基金资助项目(50905191, 51375506);中央高校基本科研业务费项目(CDJZR14285501);中国博士后科学基金资助项目(2012M521690)

收稿日期：2014-10-22修改稿收到日期：2014-12-03

中图分类号:TH132.4

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.01.010

Optimal sparse representation method for impact vibration extraction

QIN Yi1, GUO Lei1, WU Hong-gang2

(1. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China; 2. Chongqing Communication College, Chongqing 400035, China)

Abstract:Aiming at the problem of impact vibration signals extraction under strong back-ground noise and other vibration interferences, an optimal sparse representation method of impact vibrations based on basis pursuit was proposed. A sparse solving model for extracting impact vibrations was built, and a transformation basis for impact vibration feature extraction was designed. Then the energy ratio of characteristic spectral lines in the whole frequency spectrum was taken as the index for evaluating the effect of impact vibration feature extraction, and the impact vibration components were optimally obtained with this evaluation index. The proposed method was applied in simulation tests and gear fault diagnosis. The results showed that this approach can better extract the weak periodic impact components, so it is valvuable for actual applications.

Key words:sparse solution; basis pursuit; transformation basis; gear fault; feature extraction

第一作者 秦毅 男，博士，副教授，1982年8月生