复杂工况下的大型风力机气动弹性响应和尾迹数值分析研究

曹九发， 柯世堂， 王同光

(南京航空航天大学 江苏省风力机设计高技术研究重点实验室，南京　210016)



复杂工况下的大型风力机气动弹性响应和尾迹数值分析研究

曹九发， 柯世堂， 王同光

(南京航空航天大学 江苏省风力机设计高技术研究重点实验室，南京210016)

摘要：在复杂工况下，大型风力机受到载荷更加严重，导致风力机气动和结构耦合响应问题更加明显。主要针对稳态偏航、动态偏航、风剪切和随机风速场等复杂工况，采用非定常自由涡尾迹方法计算尾迹形状和气动载荷，加入了复杂工况的模型，进行了动态失速模型和三维旋转效应模型修正。在考虑气动载荷、惯性载荷和重力载荷影响下，采用有限元法结合模态法建立起风力机解耦动力学方程，并且通过Newmark方法进行数值求解该方程。实现了复杂工况数值模拟计算，比较不同复杂工况的气动弹性响应结果。最后，得出大型风力机在复杂工况下的气动性能、载荷、动态响应和尾迹叶尖涡线特性，并计算出风力机在复杂工况下的迟滞时间。这为推进自由涡尾迹方法应用于大批工况载荷计算，以及提高大型风力机载荷计算精度和设计水平等具有重要意义。

关键词：自由涡尾迹；风剪切；动态偏航；随机风速场；动态响应

随着风能技术的发展，风力机逐渐向着大型化发展。由于风力机尺寸变大，非定常因素的影响变得越来越显著，比如风剪切、随机风速场和动态偏航等。复杂工况的气动性能、载荷和气动弹性响应计算研究对于风力机设计初级阶段具有重要意义。

目前，对于风力机气动分析方法，主要有三类：叶素动量理论BEM(Blade Element Momentum)[1-2]、涡尾迹方法[3-4]和CFD(Computational Fluid Dynamics)方法[5-6]。BEM方法计算时间快，但是它是基于静态平衡尾迹假设，其中，对于动态工况，如动态偏航和动态变桨等，必须加入动态修正的经验模型进行相应工况修正，从而，不同风力机和不同动态工况，该方法会出现局限性问题，可能导致风力机气动特性和气动载荷的计算结果不准确；而CFD方法能模拟三维非稳态黏性流，但影响因素多且黏性耗散、边界层转捩等的处理有待解决[7]，而且网格量多，计算效率低，对于工程应用具有局限性；涡尾迹方法是介于BEM与CFD之间，涡流理论采用升力线或者升力面对叶片进行模拟，尾迹处理则有预定涡尾迹[4,8-9]和自由涡尾迹[10-12]，目前的涡尾迹方法还主要研究稳态风速来流工况和一些简单的非定常工况，对于复杂非定常工况研究欠缺，特别是具有风剪切的随机风速场风力机气动特性研究。涡尾迹方法适合动态复杂工况模拟计算，并且充分考虑了叶片与尾迹之间的相互干扰，非常适合于风力机气动特性分析。同时，涡尾迹方法计算效率比CFD方法高，具有与BEM方法批量计算载荷的优点，对于工程实际应用具有重要意义。

风力机气动弹性问题的结构分析方法分析过程中主要有三类模型被使用：基于工程梁理论或有限元方法的模型[13-14]；基于风力机模态分析使用模态刚度和模态质量的模型[15]；基于多体动力学方法的模型[16]。为了便于结构动力学方程的解耦，本文采用有限元法结合模态法建立风力机结构模型。

本文首先，采用自由涡尾迹方法，进行风力机非定常工况的计算结果验证分析，实现大型风力机风剪切、随机风速场和动态偏航数学模型，并且嵌入自由涡尾迹方法中；然后，考虑叶片速度和位移耦合，通过有限元法结合模态法解耦求解动力学方程，实现风力机气动和结构的双向耦合计算。最终，对稳态风速的动态偏航、风剪切的动态偏航和随机风速场算例的气动弹性响应和尾迹进行分析。

1自由涡尾迹方法

1.1尾流场描述

自由涡尾迹方法中，对风力机流场作不可压和位流假设，气动模型可以简化为来流、叶片附着涡线和自由涡面的总和，叶片附着涡线置于1/4弦线处，并采用“arc-cosine”法离散，每段附着涡线代替每段叶素，叶素控制点置于3/4弦线处，从而叶片被模拟成一个Weissinger-L升力面模型，如图1所示。自由涡面是由叶片尾缘拖出涡线形成，可分为尾随涡线和脱体涡线，分别模拟附着环量在空间和时间上的变化。尾随涡强度定义为相邻叶素的附着环量之差：

(Γt)i,j=

(1)

式中:j=1,2,…,NE，体现不同叶素。

图1　风力机尾迹离散描述示意图Fig.1 Wake discrete description of wind turbine

相邻方位角上叶素附着环量涡之差是脱体涡的强度，则第j个方位角下的脱体涡强度是：

(Γs)i,j=

(2)

式中:i=1,2,…,NT,体现不同方位角。

1.2涡线方程与求解

本文模型中每根涡线均在远场截断，流场中涡线随当地流速移动会自由卷起。涡线的偏微分控制方程可写为：

(3)

推导尾迹控制方程中的对时间步微分方程的差分，令Δψ=Δζ，可得到控制方程离散格式[12]：

预估步：

(4)

校正步：

(5)

本文动态失速模型采用L-B模型，进行风力机的适当动态失速模拟修正。根据动态失速L-B模型，可将二维翼型的非定常特性通过附着流、分离流和动态失速涡来模拟[3]。而对于三维旋转效应修正采用Du-Selig模型[3,17]。

2风速场与动态偏航工况

2.1风剪切模型

风剪切就是指稳态平均风速随高度的变化情况。在考虑风剪切时，可选用以下模型。模型中V(h)是指高度h处的风速，V(h0)是指参考高度h0处的风速。常用风剪切修正模型包括指数模型和对数模型，本文选用前者，其修正公式如下[2]：

(6)

当不考虑风剪切的影响时，可以将α的值设为0，取值范围和地表情况相对应。h0是轮毂的位置，V(h0)是轮毂的参考风速。

2.2动态偏航模型

当风轮出现动态偏航或者动态变桨时，风轮尾迹的变化也是一个非定常过程，从而导致风轮的气动特性也发生改变。

通过风向动态的改变来模拟风轮动态偏航效果。参照风力机设计认证标准GL2003，采用极端风向变化工况，其中风向随时间的函数为：

γ(t)=

(7)

式中:γe=30°，为风向变化幅值；T=6 s，为风速变化周期。

2.3随机风速模型

由于风力机运行环境中的风剪切和湍流的存在，导致来流风速发生随机性脉动变化，从而影响风轮气动特性，特别是大型风力机受其影响更明显。为了研究大型风力机在随机风速场激励下的气动特性。把风轮风速场离散化成36个空间点，基于改进Von karman随机风速频谱函数，采用小波逆变换方法[18]，仿真出相互独立的风力机随机风场，再对其进行空间相关性修正，建立起符合实际风力机运行风速场特性的随机三维风速场模型。风力机风速场嵌入自由涡尾迹方法中的流场图如图2。

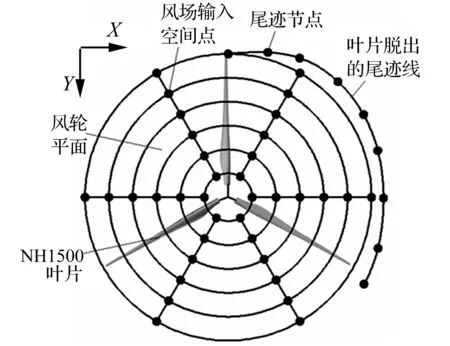
图2　自由涡尾迹方法的风速场示意图Fig.2 Wind field of the wake vortex method

3结构动力学方程建立与求解

3.1气动结构耦合方式

本文采用自由涡尾迹方法进行气动载荷计算。但是，由于涉及到气动与结构的耦合计算，因此，根据自由涡尾迹方法的特点，在采用该方法进行气动载荷计算中，会出现两个耦合项：叶片振动速度耦合项和叶片变形位移耦合项。其中，叶片振动速度耦合项主要是叶片挥舞速度和摆振速度，它们影响着每个叶素的相对速度大小，从而，每个叶素的相对速度计算可以表示如下：

(8)

式中：vrel_x和vrel_z分别是叶片摆振和挥舞方向的相对速度，v0_x和v0_z分别是叶片摆振和挥舞方向的初始来流速度，vrot是风轮旋转速度，vind_x和vind_z是流场中所有涡线对每个叶素上的摆振和挥舞方向的诱导速度，vb_x和vb_z是叶片的摆振和挥舞速度。

对于叶片变形位移耦合项是：挥舞方向位移、摆振方向位移和径向位移。在本文的自由涡尾迹方法计算中，由于尾迹的形状直接影响到流场中诱导速度的大小，因此，必须考虑叶片变形产生的位移对尾迹和诱导速度的影响。通过该项耦合可 以研究风力机在考虑叶片变形后，尾迹和流场速度的变化情况，这对于采用BEM方法来说是很难实现。并且对提高风力机载荷和流场速度计算精度，具有重要意义。尾迹位移耦合表达式可以表示如下式：

(9)

3.2有限元模型

通过模态叠加法对结构动力学进行解耦求解。系统自由振动方程的广义特征值问题为：

Kφ-ω2Mφ=0

(10)

从而可将系统的动力学方程写为式(12)。风力机简化模型如图3。通过梁单元进行叶片的模拟，轮毂和塔架采用壳单元模拟，机舱看成0D质量点。部件之间都采用刚性连接。

图3　风力机简化模型图Fig.3 The simplified model of Wind turbine diagram

本文以NH1500风力机为算例，风轮旋转速度为17.2 r/min。采用商业软件Patran/nastran，分别计算了风轮和风力机整机模态，相应的固有频率如表1所示，并且与商业软件GH Bladed计算结果对比。从表格中可以看出， 频率计算结果和Bladed软件计算结果很接近，塔架模态频率最低，风轮存在挥舞和摆振模态，并且每一阶挥舞和摆振都具有两个反对称和一个对称振型，相比固有频率而言，挥舞频率较低些。通过只有风轮模型和风力机整机模型计算值对比，可以发现整机大部分模态比只有风轮模型的固有频率低，这是由于考虑轮毂、机舱和塔架后，使得整个风力机模型刚度变小导致；并且在旋转作用下，风力机模态固有频率都被提高，可见离心力的“刚化作用”分量大于“柔化作用”分量。

表1　风力机固有频率对比

图4　考虑旋转的整机前11阶模态振型图Fig.4 11 Order modes before of the wind turbine in rotational condition

3.3结构动力学方程与求解

风力机结构系统结合模态动力方程可表示为：

(12)

式中:M是质量矩阵，C是比例阻尼矩阵，K是刚度矩阵，F(t)是广义力，x是广义位移。其中，风力机载荷包括重力，惯性力，气动力。结构阻尼本文都用0.005来进行计算。对其微分方程的求解采用Newmark方法离散求解，具体形式如下：

(13)

整个气动结构耦合求解实现过程见图5。

图5　程序求解过程示意图Fig.5 Procedure solving process diagram

4算例计算与结果分析

4.1计算程序验证与分析

为了验证本文非定常气动模型的可靠性，通过美国可再生能源实验室进行的NREL Phase VI风力机的非定常空气动力学系列实验[19]，进行验证计算与分析。

图6是稳态风速10m/s下偏航30°工况下的法向力系数Cn和切向力系数Ct。从图中可以看出，“2D计算值”和“3D计算值”叶根的气动载荷预测会比叶片中部和叶尖差，并且主要是体现在0°方位角附近(“2D计算值”是程序计算中没有加三维旋转效应修正和动态失速模型修正；“3D计算值”是自由涡尾迹方法中嵌入了Du-Selig模型三维旋转效应修正模型和LB动态失速修正模型)。通过偏航时迎角的变化情况，可得知风轮在0°方位角附近，叶片的迎角处于大迎角，并且变化幅度较大，从而存在迎角大、变化频率快的动态失速修正困难的问题，从而导致“2D计算值”在叶根处的Cn和Ct都很难与实验值匹配，然而，通过三维旋转效应和动态失速模型修正的“3D计算值”会使得数值计算值精度大大提高，但相对于叶片中部和叶尖位置的计算误差仍然较大，这需要进一步研究更好的修正模型来提高叶根的气动载荷计算精度。而对于“2D计算值”和“3D计算值”的计算精度比较，不管是叶片的展向位置来看，还是方位角来看，“3D计算值”大部分都是要比“2D计算值”好很多。因此，本文气动计算模块具有一定的可靠性。

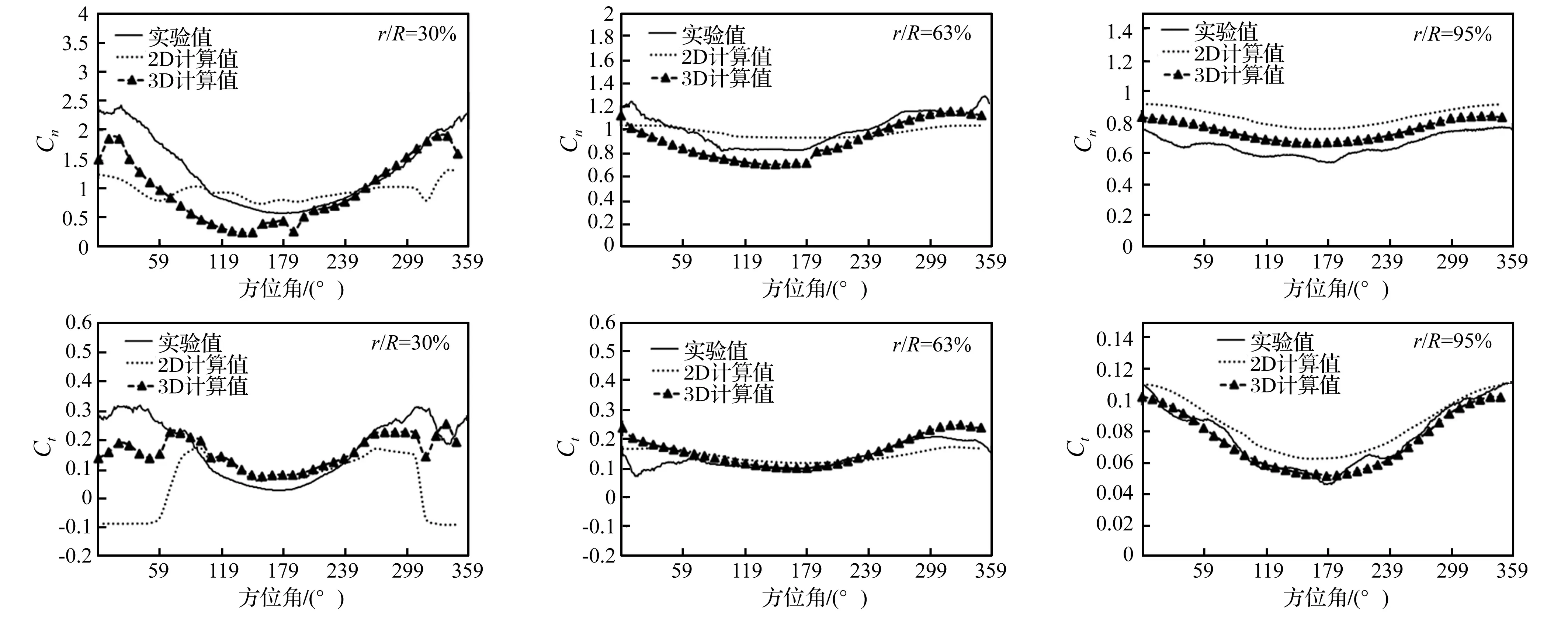
图6　稳态风速下叶片展向的Cn和CtFig.6 Variation of normal and tangential coefficient at different span with wind speed

4.2大型风力机算例结果与分析

NH1500风力机是变桨变速风力机，具体的风力机性能和几何参数见表2。针对该风力机主要进行两个算例数值计算，第一个是考虑风剪切的偏航和动态偏航对比算例；第二个是考虑风剪切的三维随机风场工况算例。采用风力机转速为17.2 r/min。其中，风速场模型的主要参数为：参考风速为轮毂处风速即10 m/s，粗糙度为0.01，采样时间为0.1 s，采样点数为8 192，风剪切指数模型的系数0.2。

表2　NH1500风力机参数

基于本文的风力机整机气动和结构耦合计算算法，模拟计算的稳态偏航和动态偏航工况都是仿真80 s，并且两个工况都考虑风剪切。

图7是动态偏航在第40 s时，风力机叶尖涡线形状图，从图中可以看出，风力机在动态偏航过程中，尾迹变化情况。其中，叶尖涡线出现了严重的不对称性，随着偏航的运动，叶尖涡线也开始缓慢地偏转，并且YZ平面可以看出风力机受到风剪切的影响整个尾迹出现“上稀疏下密集”分布特点。

图7　动态偏航40 s时的叶尖涡线图Fig.7 Tip vortex lines at 40s in dynamic yaw condition

由于在挥舞方向上气动和结构的相互影响比较明显，因此，给出了稳态偏航和动态偏航的挥舞方向的叶尖位移和叶根载荷，如图8和图9所示。(在动态偏航工况前，增加20 s进行收敛计算)。从图中可以看出，大概20 s时各个工况都已经计算收敛了，收敛之后稳态偏航工况表现出比无偏航工况振荡幅度大，并且出现响应周期曲线不对称的现象；动态偏航在25 s处开始发生叶尖位移和叶根载荷的降低，这是由于25 s开始发生偏航动作，并且其变化趋势是：逐渐减小，接着缓慢回到平衡位置，最后与稳态偏航的效应曲线重合。由此可见，在动态偏航过程中，叶尖挥舞位移和叶根挥舞载荷响应变化明显，虽然总体载荷会出现减小，但会有高频响应出现，这对于风力机疲劳具有重要影响。

图10和图11是风轮的扭矩和推力系数变化曲线，给出无偏航、稳态偏航、动态偏航和刚体风力机动态偏航的数据。从图中可以观察出，偏航、风剪切和风力机结构振动因素给风轮动态响应曲线带来的不同变化振荡幅度和非对称周期响应特点：无偏航风剪切响应曲线振荡幅度最大，而有偏航风剪切的振荡幅度减弱了，但是出现锯齿形状的非对称周期响应曲线。

相对稳态偏航，动态偏航的风轮扭矩和推力都发生了迟滞现象，并且迟滞现象会比叶尖位移和叶根载荷明显，柔性和刚性风力机扭矩迟滞时间分别为13.7 s和17.9 s。通过对比刚体风力机和柔性风力机响应曲线，出现柔性风力机有刚体3倍的响应周期，这是由于风力机叶片重力和结构振动导致了周期改变，另外使得扭矩和推力系数均值都变大了。

图8 稳态和动态偏航叶尖挥舞位移Fig.8Displacementofflapwisedirectionofbladetipinsteadyanddynamicyawcondition图9 稳态和动态偏航叶根挥舞方向剪力Fig.9Shearingforceofflapwisedirectionofbladerootinsteadyanddynamicyawcondition图10 稳态和动态偏航的风轮扭矩曲线Fig.10Torqueofrotorinsteadyanddynamicyawcondition

本文随机风速场输入工况仿真计算，该随机风速场包括三个方向：纵向风速、横向风速和垂直向风速，并且风速场包含有风剪切效应。风力机气动和结构全耦合模型进行计算，其中风力机模型为整机模型(全耦合是指速度和位移都耦合的双向动态响应计算，无耦合计算是指速度和位移不进行耦合的单向动态响应计算)。

图12为风力机叶尖位移的动态响应时间曲线图。从图中可以看出，无耦合计算的叶尖位移波动幅值大于全耦合计算结果，因此，速度和位移耦合起到了气动阻尼作用，减弱了振动幅度。图13为风轮的扭矩随时间变化曲线。从图中可以看出，在受到随机风速场的干扰后，风轮扭矩也出现随机变化趋势，并且柔性风力机扭矩和推力系数均值都比刚性风力机大，趋势与动态偏航分析的结果保持一致。由于扭矩和Cp曲线是对应关系，同时可以得出风力机气动性能在变柔性后在某些工况可以提高风能利用系数。

图11 稳态和动态偏航的风轮推力系数曲线Fig.11Thrustcoefficientofrotorinsteadyanddynamicyaw图12 随机风速场工况的叶尖挥舞位移Fig.12Displacementofflapwisedirectionofbladetipinstochasticwindspeedfieldcondition图13 随机风速场工况的风轮扭矩Fig.13Torqueofrotorinstochasticwindspeedfield

5结论

本文基于自由涡尾迹方法，针对大型风力机在复杂工况下，完成了具有风剪切效应的稳态偏航、动态偏航和随机风速场模块的数值求解程序，并且其中加入了动态失速模型和三维旋转效应模型修正。同时，通过PhaseVI风力机非定常实验数据进行验证，最后，进行了响应的数值模拟计算以及气动弹性响应、载荷和尾迹叶尖涡线分析，得出以下结论：

(1) 对几种风力机简化模型模态进行了分析，总结了无旋转风轮、有旋转风轮模型、无旋转整机模型和有旋转整机模型的固有频率特点，旋转带来的“刚化作用”分量大于“柔化作用”分量。

(2) 在动态偏航的工况尾迹分析中，动态偏航尾迹不仅体现出“上稀疏下密集”的分布风剪切特点，还捕捉到动态偏航的尾迹变化过程。这些尾迹特点的捕捉对于保证风力机载荷计算精度有重要意义。

(3) 对比了考虑风剪切的无偏航、稳态偏航和动态偏航工况的气动弹性响应特点，偏航使得响应均值的减小，并且动态偏航在完成偏航动作的过程中高频响应多于稳态偏航工况。从响应周期和响应幅度方面看，柔性风力机偏航下的风轮扭矩和推力都与刚性风力机有着明显的差别，并且柔性和刚性风力机扭矩迟滞时间分别为13.7 s和17.9 s。因此，对于大型风力机的柔性问题必须被考虑。

(4) 在随机风速场模拟计算中，叶片位移和速度的全耦合起到气动阻尼的效果，减缓了叶片气动弹性响应，并且柔性风力机的扭矩会比刚性风力机更大些。

综上所述，本文基于自由涡尾迹方法的复杂工况计算结果具有一定可靠性，并且随机风速场的嵌入，从计算时间和准确性，使得自由涡尾迹方法应用于工程的大批量工况载荷计算具有可行性。对于大型风力机的气动弹性响应分析、载荷计算、设计以及优化等具有重要意义。

参 考 文 献

[1] Rijs R P P, Jacobs P, Smulders P T. Parameter study of the performance of slow running rotors[J]. Wind Energy and Industrial Aerodyn,1992, 39(1/2/3):95-103.

[2] Burton T,Sharpe D,Jenkins N,et al.Wind Energy Handbook[M].2005.

[3] Wang T G. Unsteady aerodynamic modeling of horizontal axis wind turbine performance[D]. Glasgow: University of Glasgow, 1999.

[4] 王芳，王同光. 基于涡尾迹方法的风力机非定常气动特性计算[J].太阳能学报,2009,30(9):1286-1291.

WANG Fang, WANG Tong-guang. Wind turbine unsteady aerodynamic performance prediction based on the vortex wake method[J]. ACTA Energlae Solaris Sinica, 2009, 30(9): 1286-1291.

[5] Chaviaropoulos P K, Hansen M O L. Investigating three-dimensional and rotational effects on wind turbine blades by means of a quasi-3D Navier-Stokes solver [J]. Journal of Fluids Engineering,2000, 122(2): 518-548.

[6] Sandersen B, Pijl S P, Koren B. Review of computational fluid dynamics for wind turbine wake aerodynamics [J]. Wind Energy, 2011, 14(7): 799-819.

[7] Vermeer L J，Sorensen J N,Crespo A．Wind turbine aerodynamics[J] ．Progress in Aerospace Sciences,2003(39)：467-510.

[8] Coton F N, Wang T. The prediction of horizontal axis wind turbine performance in yawed flow using an unsteady prescribed wake model [J]. Proceedings of the Institution of Mechanical Engineers, Part A, Journal of Power and Energy,1999, 213: 33-43.

[9] Wang T, Coton F N. An unsteady aerodynamic model for HAWT performance including tower shadow effects [J]. Wind Engineering,1999,23: 255-268.

[10] Sebastian T, Lackner M A. Development of a free vortex wake method code for offshore floating wind turbines [J]. Renewable Energy, 2012, 46: 269-275.

[11] Zhou W P, Tang S L, LÜ H, Computation on aerodynamic performance of horizontal axis wind turbine based on time-marching free vortex method [J]. Chin.Soc.for Elec.Eng., 2011, 31(29):124-130.

[12] 许波峰.基于涡尾迹方法的风力机气动特性研究[D]. 南京:南京航空航天大学，2013.

[13] 柯世堂, 王同光, 赵林, 等. 风力机风振背景、共振响应特性及耦合项分析[J]. 中国电机工程学报, 2013,33(26):101-108.

KE Shi-tang, WANG Tong-guang, ZHAO Lin, et al.Background, resonant components and coupled effect of wind-induced responses on wind turbine systems[J]. Proceeding of the CSEE, 2013,33(26): 101-108.

[14] 任勇生, 张明辉. 水平轴风力机叶片的弯扭耦合气弹稳定性研究[J]. 振动与冲击, 2010, 29(7): 196-200.

REN Yong-sheng, ZHANG Ming-hui. Aeroelastic stability study on coupled flutter for horizontal axis wind turbine blades[J]. Journal of Vibration and Shock, 2010, 29(7): 196-200.

[15] Hansen M O L. Aerodynamics of wind turbines[M].Second Edition,Earthscan,2008.

[16] Schiehlen W. Multibody system dynamics: Roots and perspectives[J]. Multibody System Dynamics, 1997, 1: 149-188.

[17] Du Z, Selig M S. A 3-D stall delay model for horizontal axis wind turbine performance prediction[R]. AIAA-98-0021, 1998.

[18] Kitagawa T, Nomura T. A wavelet-bassed method to generate artificial wind fluctuation data[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91:943-964.

[19] Hand M M, Simms D A, Fingersh L J, et al. Unsteady aerodynamics experiment Phases Ⅵ: Wind tunnel test configurations and available data campaigns[R]. Golden: National Renewable Energy Laboratory, NREL/TP-500-29955, 2001.

基金项目：国家973计划项目(2014CB046200)大型风力机的关键力学问题研究及设计实现；国家自然科学基金(51208254)复杂环境下超大型冷却塔风振机理与等效静风荷载研究；江苏高校优势学科建设工程资助项目

收稿日期：2014-09-23修改稿收到日期：2014-12-03

通信作者王同光 男，教授，博士生导师，1962年生

中图分类号:O357; TK89

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.01.009

Numerical analysis for aero-elastic responses and wake of a large scale wind turbine under complicated conditions

CAO Jiu-fa, KE Shi-tang, WANG Tong-guang

(Jiangsu Provincial Key Laboratory of Hi-Tech Research for Wind Turbine Design, Nanjing University of Aeronautics & Astronautics, Nanjing 210016, China)

Abstract:Large scale wind turbines suffer serious unsteady loads under complicated conditions, it leads to their obvious aero-elastic coupled responses. For steady yaw, dynamic yaw, wind shear and stochastic wind field, the free vortex method was used to calculate their aerodynamic loads and wake shapes. The dynamic stall model and the three-dimension stall delay model were taken into account. At the same time, considering the aerodynamic load, inertial load and gravity load, the finite element method was combined with the modal method to build the decoupled dynamic equations of a wind turbine, these equations were solved numerically with Newmark method. The aero-elastic dynamic responses under different complicated conditions were compared. Finally, the aerodynamic performance, load, dynamic responses and tip vortex line characteristics of wind turbines were deduced under complicated conditions. The results were significant for applying the free vortex method in load calculations of wind turbines, and improving the load calculations accuracy and design levels of large scale wind turbines.

Key words:free wake method; wind shear; dynamic yaw; stochastic wind field; dynamic response

第一作者 曹九发 男，博士生，1986年生

邮箱: tgwang@nuaa.edu.cn