惯性边界下带钢的非线性振动分析

高崇一， 杜国君， 李建雄， 胡发科

(1. 燕山大学 河北省重型装备与大型结构力学可靠性重点实验室，河北　秦皇岛　066004;2.燕山大学 电气工程学院自动化系，河北　秦皇岛　066004)



惯性边界下带钢的非线性振动分析

高崇一1， 杜国君1， 李建雄2， 胡发科1

(1. 燕山大学 河北省重型装备与大型结构力学可靠性重点实验室，河北秦皇岛066004;2.燕山大学 电气工程学院自动化系，河北秦皇岛066004)

摘要：根据连轧机轧制过程中带钢与轧辊的运动机理，将相邻两机架间的带钢简化为轴向运动的Euler梁，轧辊简化为定轴转动的惯性元件，建立Euler梁在惯性边界下的非线性振动力学模型。基于哈密顿原理建立轴向运动Euler梁的纵向和横向非线性振动微分方程，利用Kantorovich时间平均法简化运动方程和边界条件，并采用修正迭代法求解运动方程。最后通过数值计算获得了Euler梁非线性振动的幅频响应曲线，并讨论惯性边界条件下的轴向运动速度、长度和轧辊的转动惯量对Euler梁振动特性的影响。研究结果可为控制和分析连轧过程中带钢垂直振动提供重要的理论参考。

关键词：Euler梁；惯性边界；带钢；垂直振动；修正迭代法

轧机振动普遍存在于轧制生产中，复杂的振动现象是导致带钢表面缺陷的重要因素，并且影响设备关键部件的使用寿命。关于轧机振动问题的研究涉及轧机系统各个部件的不同振动形式，如轧辊的垂直振动、水平振动、轴向串动、带钢的横向和纵向振动、主传动系统的扭转振动和轴向振动等[1]。其中带钢的横向(垂直)和纵向振动方面的研究相对较少，而连轧中带钢的振动又是轧制过程中不可避免的。因此，对带钢振动的研究成了钢铁行业亟待解决的重要问题。

轧制过程中，带钢的垂直振动对轧机和产品质量的影响相对较大。若忽略轧机辊系的垂直振动，可将带钢简化为轴向运动梁[2-4]，带钢垂直振动可等效为运动梁的横向振动，从而可以利用运动梁理论分析带钢振动。刘明哲等[3]建立了运动板带的二维动力学模型和三维动力学模型，并利用数值方法分析了轧制过程中运动带钢的固有特性和稳定性。Sun等[4]考虑两机架间带有时变张力的运动带钢的非线性振动模型，并采用多尺度法求解。Bor等[5]在冷连轧过程中分析了含有非线性参数的自激振动现象，并给出了近似解析解。Miranker[6]首次推导出了运动弦线横向振动的运动微分方程，并对Euler梁进行了相应分析。Mote[7]分析了轴向变速运动系统的横向振动稳定性问题。陈树辉等[8]对轴向运动Euler梁非线性振动内共振进行了研究。Suweken等[9-10]研究了考虑两端边界条件下的轴向运动Euler梁的振动特性。

带钢振动的研究大多是基于简支、固支或带有扭转弹簧的边界条件[11]，而忽略了轧辊转动惯量的影响，与轧制过程的实际偏离较大。本文考虑轧辊的转动惯量对带钢垂直振动的影响，并且基于轴向运动梁理论[12-13]，在不考虑剪切变形的情况下，可将带钢振动等效为Euler梁振动，建立轧辊与Euler梁相互作用的动力学模型，求解惯性边界条件下轴向运动梁的非线性振动。本文采用修正迭代法[14-15]求解轴向运动Euler梁振动方程，并利用Matlab对系统进行数值仿真，研究系统各参数对带钢非线性振动特性的影响，为带钢连轧生产中的优化控制提供理论参考。

1模型的建立

图1　机架间运动带钢及其等效的Euler梁力学模型Fig.1 Moving strip between stands and mechanical model of Euler beam

根据哈密顿原理，对轧制过程中的力学模型进行分析，建立数学模型。轴向运动Euler梁的动能T1为：

(1)

式中:ρ为带钢密度，A为Euler梁的横截面积，u,t与u,x0分别为函数u(x0,y0,t)对变量t与x0的一阶偏导。后文中u,x0x0表示u(x0,y0,t)对x0的二阶偏导，依次类推，其他类似符号表示含义类同。

Euler梁的形变势能U为：

(2)

式中:E为弹性模量，I为惯性矩。

轧辊的动能T2为：

(3)

式中:r为轧辊半径。

由哈密顿方程：

(4)

可得出惯性边界下Euler梁的运动方程：

EAw,x0w,x0x0=0

(5)

(6)

边界条件为：

x0=0或x0=l时，

(7)

w(0)=w(l)=w,x0x0(0)=

w,x0x0(l)=0;wmax=φm

(8)

多数情况下，带钢横向振动引起的轴向运动动能相对较小，可令u,t=u,tt=0，则式(5)可简化为：

(9)

若忽略带钢轴向位移对垂直振动的影响，得出的运动方程与文献[4]一致。本文数学建模时，将轴向位移与轧辊惯性边界条件对带钢垂直振动的影响加以考虑，所得运动方程更加精确。

(10)

(11)

边界条件整理为：

x0=0或x0=l时，

(12)

(13)

为使以下运算简便，引入无量纲量

将上式代入运动方程(10)、(11)和边界条件(12)、(13)，进行无量纲化，则Euler梁的运动方程整理为：

(v02-1)φ,xx-φ,xφ,xx=0

(14)

φ,xxxx+Sv02φ,xx-ω2φ-

(15)

边界条件为：

x=0和x=1，

(16)

φ(0)=φ(1)=φ,x(0)=

(17)

2非线性方程的解

由于求解方程(14)～(17)过程较为复杂，因此，本节将采用修正迭代法进行求解。

2.1一阶近似解

首先，将方程(15)中所有非线性项略去后，可写为

φ1,xxxx-ω2φ1=0

(18)

求出方程(18)的级数解：

φ1(x)=a0M0(x)+a1N0(x)+

a2I0(x)+a3K0(x)

(19)

式中:

然后，将φ1(x)代入边界条件 (17)可解得近似的一阶频率ω1=16.71，可求出系数

a0=0，a1=0，a2=μ1φm，a3=μ2φm

其中:

从而得出

(20)

接下来将φ1(x)代入到方程(14)中得出：

(21)

由边界条件(16)得：

2.2二阶修正迭代解

下面进行二阶迭代，将求得的φ1(x)和φ1(x)代入方程(15)并简化后得：

φ2,xxxx-ω2φ2=αφ1,xx+βφ1,x2φ1,xx

(22)

式中:

其中:

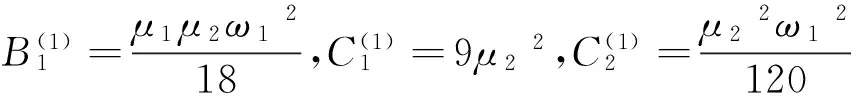
(n=2,3…)

(n=2,3…)

(n=3,4…)

由级数解的性质，方程(22)的解可写成如下形式：

其中:A0=B0=C0=C1=D0=E0=F0=0

ζ1和ζ2为待定系数。

将φ2(x)代入边界条件 (17)，可得：

Dξ=0

(24)

其中:

由detD=0可求出振频ω2的解析表达式。由式(24)可求出系数ζ1和ζ2，从而可求得振幅φ2的解析表达式，二阶修正迭代解得以确定。

3算例与讨论

对文献[16]中的轧机系统进行数值模拟，带钢厚度h为2 mm；轧制速度为5 m/s，则Euler梁无量纲轴向速度v0为1×10-3；轧辊转动惯量J无量纲量为K，当K=5，且长度l分别为1.0 m、1.5 m、2.0 m、2.5 m、3.0 m、3.5 m时，考虑振幅φm对振频ω的影响，其幅频响应曲线如图2所示，图中φm为带钢振幅无量纲量φ的最大值。在轧辊转动惯量不变的情况下，Euler梁的长度对幅频响应特性影响较大，它将改变振动性态。从图2中可以看出，当l=1.0～3.5 m时，Euler梁的振动性态逐渐由硬化型过渡到软化型，当梁长l取值为1.0 m、1.5 m、2.0 m时振动性态表现为硬化型，即随着振幅增大频率逐渐增大，且随着梁长增大，硬化程度逐渐降低；当梁长l取值为2.5 m、3.0 m、3.5 m时，曲线表现为递减趋势，非线性表现为软化型，即随着振幅增大频率逐渐减小，并呈现出软化程度增强的趋势。随着长度的递增，幅频响应曲线振动性态呈现出较均匀的变化，其中硬化型与软化型的分界在梁长l为2.0～2.5 m区间。基于上述分析，可以得出，在轧制速度和轧辊转动惯量一定的情况下，机架间距对带钢振动的幅频特性具有较大影响。根据不同机架间距下带钢振动幅频响应曲线，可对相关参数进行适当调节，以减小带钢振动对产品质量的影响。

图3为不同振幅下K值与频率的关系曲线，当Euler梁的长度l=2.0 m时，轴向速度v0=1×10-3，且振幅分别为0.05、0.10、0.15、0.20、0.25时，考虑K值对振频的影响，其中K值变化体现出轧辊转动惯量的变化。随着K值的增大，Euler梁的振频逐渐增大，K值在由0增大到5的过程中，曲线呈现出大幅度递增趋势，说明此区间的K值对振频的影响较大，并且每条曲线在K=1.5附近近似交于一点，此时对应的振频(ω=16.71)与基频一致。而随着K值继续递增，曲线又趋于平缓。随着K值的无限增大，Euler梁的边界条件无限趋近于固支状态，振频趋近于固支条件下的频率，此时近似为轧辊不转动，将带钢两侧轧辊视为固定支架的情况。另外，由图3可以看出，振幅φm越小，随K值变化曲线越早趋于平缓，振幅φm越大，K值对频率的影响范围越大，影响越明显。

图4为不同K值(轧辊转动惯量)下的速度与频率关系曲线，当梁长l=2.0 m，振幅φm=0.15，且K值分别为5、10、15、20、25时，考虑速度v0对振频的影响。从图中可以看出，不同K值下的振动频率随轴向速度增大而减小，并且，随着v0的不断增大，振频减小率呈现出增大的趋势，即轧制速度越大，速度变化对带钢振动频率的影响越大，且频率减小的越快。当K值为15、20、25时，v0-ω2关系曲线近乎重合，可以看出轧辊转动惯量无限大的情况下，边界条件趋近于固支状态。

图2 不同梁长下的幅频响应曲线Fig.2Theamplitudefrequencyresponsecurvesunderthedifferentlengthsofthebeam图3 不同振幅下K值与频率关系曲线Fig.3Kandfrequencycurvesunderthedifferentamplitudes图4 不同K值下速度频率关系曲线Fig.4VelocityandfrequencycurvesunderthedifferentK

通过图3和图4还可以看出，轧辊的转动惯量对带钢振动的影响尤为突出，在转动惯量较小时，对带钢振动影响较大，研究带钢振动时需要考虑轧辊转动惯量对其影响；在转动惯量较大时，可以近似忽略其对带钢振动的影响。

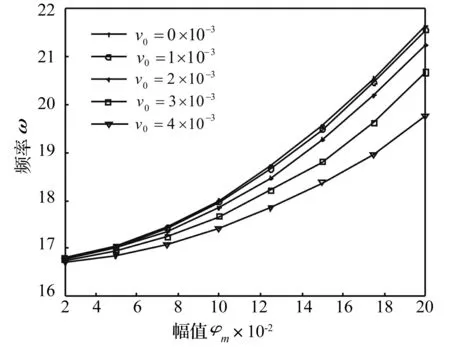
图5　不同速度下幅频响应曲线Fig.5 The amplitude frequency response curves under the different velocities

图5为不同速度下的幅频响应曲线，当Euler梁的长度l=2.0 m，K=5，轴向速度v0分别为0×10-3、1×10-3、2×10-3、3×10-3、4×10-3时，振幅φm对振频的影响。从图中可以看出，随着振幅φm的增大，Euler梁的振频逐渐增大。当轴向速度v0为0或1×10-3时，两条曲线几乎重合，可以看出当速度很小时，振幅φm对频率的影响较大；而随着速度v0增大，曲线渐渐趋于平缓，说明轧制速度越大，带钢振动的振幅φm对频率的影响越小。

4结论

模拟轧制过程中轧辊与带钢的运动，将其近似为惯性边界条件下的Euler梁，并建立其力学模型和数学模型，采用修正迭代法求解方程，并通过数值计算方法，讨论了相邻两机架间带钢的振幅、长度、轧制速度和轧辊的转动惯量对带钢振频的影响。

(1) 在轧制速度和轧辊转动惯量一定的情况下，机架间距大小对带钢振动性态的影响。当机架间距较小时，即l≤2.0 m，随着振幅的增大，振频响应逐渐增强，非线性表现为硬化型，随着机架间距由小逐渐变大，带钢振动性态的非线性硬化程度逐渐减弱。随着机架间距继续增大，幅频曲线呈现出振频随着振幅的增大而逐渐减小的趋势，即振动性态表现为软化型，并且，随着机架间距的增大，软化程度逐渐加强。

(2) 在机架间距一定的情况下，轧辊转动惯量对带钢振频的影响。轧辊转动惯量较小时，其值的大小对带钢振动性态影响较大，随着转动惯量的无限增大，边界条件趋于固支状态，轧辊转动惯量对带钢振动的影响可近似忽略。

(3) 在机架间距和轧辊转动惯量一定的情况下，轧制速度对带钢振频的影响。轧制速度较小时，带钢振频受振幅变化影响较大，随着轧制速度的不断增大，振频受振幅影响逐渐减小。

以上所得结论均基于所建立的具有惯性边界条件下Euler梁非线性振动模型，可为工程实际提供一定的理论依据。

参 考 文 献

[1] 侯福祥, 张杰, 曹建国, 等. 带钢冷轧机振动问题的研究进展及评述[J]. 钢铁研究学报, 2007, 19(10): 6-11.

HOU Fu-xiang, ZHANG Jie,CAO Jian-guo, et al. Review of chatter studies in cold rolling[J]. Journal of Iron and Steel Research, 2007, 19(10): 6-11.

[2] Han S M, Benaroya H, Wei T. Dynamics of transversely vibrating beam using four engineering theories[J]. Journal of Sound and Vibration, 1999, 225(5): 935-988.

[3] 刘明哲, 孙建亮, 彭艳, 等. 连轧过程运动带钢稳定性研究[J]. 冶金设备, 2009,31(5): 24-28.

LIU Ming-zhe, SUN Jian-liang, PENG Yan, et al. Stabilityresearch of moving strip in the rolling process[J]. Metallurgical Equipment, 2009,31(5): 24-28.

[4] Sun J L, Peng Y, Liu H M. Non-linear vibration and stability of moving strip with time-dependent tension in rolling process[J]. Journal of Iron and Steel Research, International, 2010, 17(6): 11-15.

[5] Bar A, Swiatoniowski A, Interdependence between the rolling speed and non-linear vibrations of the mill system[J]. Journal of Materials Processing Technology, 2004,155-156: 2116-2121.

[6] Miranker W L. Thewave equation in a medium in motion[J]. IBM Journal of Research and Development, 1960, 4: 36-42.

[7] Mote C D Jr. Stability of systems transporting accelerating axially moving materials[J]. Journal of Dynamic Systems Measurement and Control Transactions, 1975, 97: 96-98.

[8] 陈树辉, 黄建亮. 轴向运动梁横向非线性振动的内部共振研究[J]. 力学学报, 2005, 37(1): 57-63.

CHEN Shu-hui, HUANG Jian-liang. Study of the laterally nonlinear vibration of axially moving beams[J]. Acta Mechanics Sinica, 2005, 37(1): 57-63.

[9] Suweken G, Van Horssen W T. On the transversal vibrations of a conveyor belt with a low and time-varying velocity, Part II: the beam like case[J]. Journal of Sound and Vibration, 2003, 267(12): 1007-1027.

[10] 王波, 陈立群. 微分求积法处理轴向变速黏弹性梁混杂边界条件[J]. 振动与冲击, 2012, 31(5): 87-91.

WANG Bo, CHEN Li-qun. Treatinghybrid boundary condition of an Aaxially accelerating viscoelastic beam via a differential quadrature scheme[J]. Journal of Vibration and Shock, 2012, 31(5): 87-91.

[11] 王洋, 许飞, 李勇, 等. 带钢-辊子-柔性支承混杂系统动力学建模与耦合振动研究[J]. 振动工程学报, 2013, 26(4): 599-607.

WANG Yang, XU Fei, LI Yong,et al, Dynamic modeling and coupling vibration analysis of hybrid systems consisting of strip rolls and flexible supports[J]. Journal of Vibration Engineering, 2013, 26(4): 599-607.

[12] 杨晓东,陈立群. 黏弹性轴向运动梁的非线性动力学行为[J]. 力学季刊, 2005, 26(1):157-162.

YANG Xiao-dong, CHEN Li-qun.Nonlinear dynamical behaviors of an axially moving visco-elastic beam[J]. Chinese Quarterly of Mechanics, 2005, 26(1):157-162.

[13] Chen L Q, Yang X D. Steady-state response of axially moving viscoelastic beams with pulsating speed: comparison of two nonlinear models[J]. International Journal of Solids and Structures, 2005, 42: 37-50.

[14] 李东, 刘人怀. 修正迭代法在波纹圆板非线性振动问题中的应用[J]. 应用数学和力学, 1990, 11(1): 10-15.

LI Dong, LIU Ren-huai. Application ofmodified iteration algorithm in non-linear vibration problem of circular plate with shallow[J]. Applied Mathematics and Mechanics, 1990, 11(1): 10-15.

[15] 杜国君. 夹层圆板的大幅度振动[J]. 应用数学和力学, 1994, 15(5): 435-445.

DU Guo-jun. Largeamplitude vibration on circular sandwich plate[J]. Applied Mathamatics and Mechanics, 1994, 15(5): 435-445.

[16] 高崇一, 杜国君, 张忠健. 考虑多间隙影响的轧机主传动系统扭振分析[J]. 机械工程学报, 2014, 50(3): 130-136.

GAO Chong-yi, DU Guo-jun, ZHANG Zhong-jian, Torsionalvibration analysis of the main drive system of a rolling mill with impact of multi-clearance[J]. Journal of Mechanical Engineering, 2014, 50(3): 130-136.

基金项目：河北省教育厅科学研究计划重点项目(ZD2015077)；河北省高等学校创新团队领军人才培育计划项目(LJRC013);国家自然科学基金资助项目(61403332)

收稿日期：2014-09-02修改稿收到日期：2014-11-06

通信作者杜国君 男，博士，教授，博士生导师，1961年12月生

中图分类号:TH113.1;TG333.11

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.01.002

Nonlinear vibration of strip steel under inertial boundary conditions

GAO Chong-yi1, DU Guo-jun1, LI Jian-xiong2, HU Fa-ke1

(1. Hebei Provincial Key Laboratory of Mechanical Reliability for Heavy Equipment and Large Structures, Yanshan University, Qinhuangdao 066004, China;2. Department of Automation, College of Electrical Engineering, Yanshan University, Qinhuangdao 066004, China)

Abstract:According to the movement mechanism of strip steel and rollers in rolling process of a tandem mill, the strip steel between two neighboring stands was simplified to an axially moving Euler beam and rollers were simplified to inertia components rotating about a fixed axis, the nonlinear vibration mechanical model of the beam under inertial boundary conditions was established. The longitudinal and lateral vibration equations of the beam were derived with Hamilton principle. Kantorovich averaging method was used to simplify the motion equations and the inertial boundaries, and the modified iteration method was employed to solve the motion equations. Finally, based on the results of numerical calculation, the amplitude-frequency response curves of the beam were obtained, and the influences of beam axial velocity, beam length and rotational inertia of roller on the vibration performance of the beam under conditions of inertial boundary were discussed. The results provided an important theoretical reference for controlling and analyzing the vertical vibration of strip steel in a continuous rolling process.

Key words:Euler beam; inertial boundary; strip steel; vertical vibration; modified iteration method

第一作者 高崇一 女，博士生，1986年8月生