深基坑开挖过程水平位移影响数值分析

贺湘灵（海峡（福建）交通工程设计有限公司，福建 福州 350000）

深基坑开挖过程水平位移影响数值分析

贺湘灵
（海峡（福建）交通工程设计有限公司，福建 福州 350000）

深基坑工程在进行开挖施工的过程中，势必会对四周的建筑物、构筑物以及市政工程造成一定的影响，其中主要影响为深基坑的水平位移，水平位移超过一定限值，引起四周土体的不均匀沉降，导致建筑构筑物破坏。本文以某地铁车站为研究对象，通过有限元软件模拟了深基坑的开挖过程，得到了土体和支护结构随着深基坑开挖的水平位移和受力的变化情况。通过对变形因素的讨论，得出不同因素对变形影响的敏感性，从而找出影响变形的敏感因素，为设计优化提供了方法和依据。

深基坑；水平位移；有限元

引言

越来越多的城市建设正在探求地面空间、地上空间以及地下空间的整体开发，从根本上解决城市用地空间的不足和社会经济发展之间的矛盾。对深基坑工程支护结构进行设计，依据基坑工程所处区域的周边环境的要求，根据周围环境的允许基坑变形值以及基坑土体性质，对基坑支护结构的水平位移进行分析计算。通常情况下，对于一般民用建筑而言，当建筑物的相对倾斜为1/300时，则会致使建筑结构外墙出现开裂的现象，当建筑物的相对倾斜超过1/150时，则会致使建筑物结构出现结构性破坏，严重危急建筑物使用安全[1]。

图2-1 基坑横剖面图

1 数值模拟概述

岩土工程结构的数值解是依据满足了基本方程与边界条件的前提下共同推导得出的。差分法采用差分方程即代数方程的形式近似的代替了基本方程的形式，从而使对微分方程求解的问题便转换成为了对高阶代数方程组进行求解的问题[2]。FLAC3D是二维有限差分程序FLAC2D的扩展，采用ANSIC++语言编写。该程序可以通过单个的流体质点的运动参数随着时间的变化规律，以及相邻质点问的这些参数的变化规律来对整个流场中的流体运动进行研究[3]。在本文数值模拟过程当中，分析模型选择使用的二维有限元，土体本构关系选择Druck-Prgaer模型，地下连续墙选择使用梁单元，基坑支撑使用杆单元，基坑地下连续墙和土体之前的相互作用力通过选择使用“滑动库仑摩擦模型”进行模拟分析。

2 工程概况

本文通过对某地铁车站的基坑工程作为研究对象。该地铁车站的基坑工程拟定开挖深度为16.8m，开挖宽度为16.8m，开挖长度为199.5m。该基坑工程围护结构的设计等级为一级，地面最大准许沉降值范围为≤0.001H，基坑围护结构的最大允许水平位移为≤0.0014H。因为该基坑工程的地址条件较为复杂并且存在较为丰富的地下水，所以基坑围护结构选择使用厚度为500mm的地下连续墙，该围护长度为28.6m，入土深度为11.5m，横向支撑选择使用4道直径600mm钢管，竖向间距分别为5m、4m和4m。在基坑工程完成开挖之后适时安设钢支撑并施加预应力与钢支撑，预应力施加的原则是取50%的设计轴力，实际施工过程中，预应力施加大小可以根据实际需求进行一定范围内的优化调整。

3 基坑水平变形影响分析

3.1 水平位移监测

在基坑开挖过程中对水平位移进行实时监测，监测数据分析中要注意的警戒标准有两种，其一是最大允许值，其二是变化速率。这两种指标中有一种达到警戒值都需要及时作出判断，形成决策。根据《建筑基坑工程监测技术规范》

(GB50497.2009)要求，水平位移警戒标准值为：累计水平位移达30mm或水平位移5mm/d，累计沉降值达20mm或沉降速率达3mm/d[4]。

3.2 水平位移有限元结果

对基坑工程开挖施工的有限元模拟分析，不仅仅需要对基坑工程涉及的各种材料自

身非线性特征进行考量，而且需要充分考虑到基坑开挖所导致的途径依赖性和非线性。本文选择使用“空气单元”的方法实现对该过程的模拟，对开挖掉的基坑微元赋以非常小的值，将“空气单元”的荷载、质量、应变等参数均设置为零，不必重新进行网格划分，提高模拟分析的效率[5]。

基坑开挖的过程是一个不断屈服、流变的过程，也是土体和基坑围护结构等结构不断出现变形并且达到新平衡的过程。图4-1给出了不同工况下基坑土体水平位移的有限元云图。

图4-1不同开挖阶段基坑土体水平位移的有限元云图

从以上云图能够得知，基坑土体开挖导致基坑周围的大部分土体向坑内移动，基坑被动区土体最大水平位移通常情况之下都出现在基坑开挖面之下的一定距离，并且这个最大位移的产生位置随着基坑开挖深度的不断增加而逐渐往下发展，与被动区相对应的主动区土体水平向最大位移总体上略微向上偏一点且范围较大。

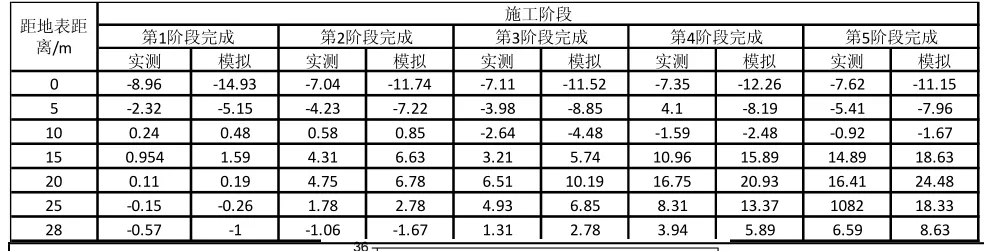
表3-1 墙体水平位移监测值与模拟值对照表(mm)

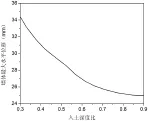
图3-1 不同入土深度下的墙体最大水平位移

对比数值模拟结果数据和实际监测数据可明显地看出，不同开挖阶段的水平位移模拟值都比相应的实测值大，施工完成后在墙体最大水平位移模拟值为24.48mm相对应的实测值为16.41mm，两者相差8.07mm，这是由于模拟时所取模型及参数的不精确性造成的。对各步施工完成后的模拟值和实测值进行系统地对比分析，可得出两者间存在一种比例关系，比例系数一般在1.5左右。

3.3 墙体入土深度影响分析

对于存在内支撑的基坑工程，嵌固深度的增加对于基坑侧向变形和基坑地表沉降影响并不显著，而且基坑围护的入土深度直接和工程造价相关联，所以，在满足基坑整体稳定性的基础之上，需要通过其他措施对墙体变形进行控制。图3-1表示的是不同入土深度下的墙体最大水平位移。

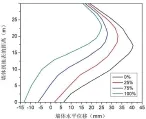
图3-2 不同支撑预应力下墙体变形曲线

3.4 支撑预应力影响分析

对钢支撑分别施加大小不一的预应力进行模拟分析，得出基坑地表最大变形曲线如图3-2所示。从图中可以看出，施加在钢支撑上的预应力值为75%设计轴力时，基坑墙体最大水平位移降低了40%，所以，对基坑支撑施加一定程度的预应力能够有效控制墙体变形，当施加在钢支撑上的预应力值超过75%设计轴力时，再增大预应力值对基坑变形的控制并没有太多效果，所以比较合理的基坑支撑预应力施加值为设计轴力的50～70%。

4 结语

本文通过FLAC3D程序模拟某地铁车站的深基坑工程开挖过程，因为土体模型受环境影响较大使数值模拟过程与实际工程结果有一定偏差，但有限元结果对深基坑工程仍有一定指导意义。通过有限元模拟分析可以得出，一旦基坑工程的嵌固深度大于0.9～1.0H，此时继续增加入土深度并不会对基坑变形的降低起到作用，所以，只需要计算出基坑围护结构的最小入土深度即可保证基坑的整体稳定性。如需改善基坑墙体的内外侧土体受力情况，可以对支撑结构施加一定的预应力，以此增加主动土压力，降低被动土体压力，通过此手段对基坑工程的各项变形指标起到一个较为有效地控制效果。

[1]孙凯华, 谭勇强. 高层建筑物抗地表倾斜变形影响能力的初步分析[J]. 煤矿开采, 2009, 14(4):49-51.

[2]孙晓俐. 大连衡隆广场深基坑工程稳定性数值模拟分析[D]. 桂林理工大学, 2012.

[3]许薇, 葛文璇. “结构力学”习题课的改革与探索[J]. 中国电力教育, 2012(25):56-56.

[4]GB50497-2009《建筑基坑工程监测技术规范》

[5]徐杨青, 王永宁, 程杰林. 模拟深基坑开挖和支护全过程的有限元数值分析[J]. 岩土力学, 2002, 23(z1).

G322

B

1007-6344（2016）04-0323-02

贺湘灵（198401-），男，湖南长沙人，硕士研究生；