弯应矩和扭应矩作用下的疲劳强度研究
念红芬 韩文坝黄双华(攀枝花学院,四川攀枝花 67000)
弯应矩和扭应矩作用下的疲劳强度研究
念红芬 韩文坝1黄双华1
(攀枝花学院,四川攀枝花 617000)
现行弹性理论不能解决轴扭转和梁弯曲的部分不平衡问题。但“非零应矩弹性理论”证明了扭转存在扭应矩,弯曲存在弯应矩,扭转剪应力和弯曲正应力都不是真应力,只是相当应力,从而找到了上述不平衡问题的根源。本文用“应矩理论”修正了“应力理论”的疲劳强度公式,从而找到了工程疲劳断裂事故产生的原因。
疲劳;循环;应力;应矩
动载荷作用下的金属疲劳断裂事故经常突然发生,防不胜防,给人类的生命财产造成了极大的损失。究其原因,除质量原因外,主要是现行弹性理论的关于正应力与剪应力结论有缺陷造成的。这种缺陷可以用新理论《非零应矩弹性理论》[1]加以修正。
1 和疲劳有关的新理论简介
新理论修正了 “作用在单位面积上的力矩(弯矩和扭矩)的极限(应矩)为零[2]”的结论,证明了外力作用下的弯应矩和扭应矩为非零。而现行弹性理论认为纯弯曲正应力σ为零,纯扭转剪应力τ为零,是平衡的,从而无法解决大量的弯曲和扭转不平衡的实例。
(1)新理论推导出受扭矩Mn、直径为D的圆轴扭转最大扭应矩[1]为
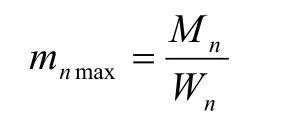
式中:Wn——新理论下的圆轴抗扭截面模量。
(2)新理论推导出的圆轴弯曲最大弯应矩[1]

式中:WW——新理论下圆轴的抗弯截面模量。

(3)绝对静矩:[1]
2 交变应矩下的疲劳[2]
2.1 引起金属疲劳的原因
如图1(a),火车轴上所受到的作用不是应力,而是弯应矩。

图1 交变弯应矩引起疲劳
如图1(a)所示,A点到中性轴的距离y为:

式中,r为轴的半径;ω为角速度;t为时间。
如图1(b)所示。而应矩理论下的弯应矩由下式[1]确定:

如图1(c)。可见构件所受到的是交变应矩,而不是交变应力。因此,受弯应矩和扭应矩作用产生的金属疲劳不是应力引起的,而是应矩引起的。只有受拉-压应力作用产生的疲劳,才是应力引起的。
2.2 交变应力和应矩的循环特征[3]
图2(a)所示为按正弦变化的应力与时间t间的关系;应矩与时间t间关系如图2(b)所示。

图2 交变应力和交变应矩的循环特征
式中,σmax、σmin和mmaxw、mminw分别表示最大、最小应力和弯应矩。
若交变应矩(力)的mmax(σmax)和mmin(σmin)大小相等,符号相反时,如图1(b)所示,称为对称循环:

应改为:

式中:σm、mm为平均应力、平均应矩;σa、ma为应力幅、应矩幅。
3 影响持久极限的因素[4]
3.1 构件外形的影响
构件上有槽、孔、缺口、轴肩,将引起应力集中、局部区域形成疲劳裂纹,使持久极限显著降低。在对称循环下,若以(mw-1)d或 (mn-1)d表示无应力集中的受弯或受扭光滑小试件的持久极限;(mw-1)k或(mn-1)k表示有应力集中试样,且尺寸与无应力集中试件相同,则比值为

Kw、 Kn称为弯曲、扭转有效应矩集中系数。两种理论下的有效集中系数完全相等,即

这表明应力理论给出的有效应力集中系数的曲线和表格与应矩理论完全相同,只是把图中的材料的拉应力强度极限σb转换成材料的弯曲强度极限mb。其中

3.2 构件尺寸的影响[4]
对称循环下,光滑小试件与大试件的持久极限m-1、(m-)d之比
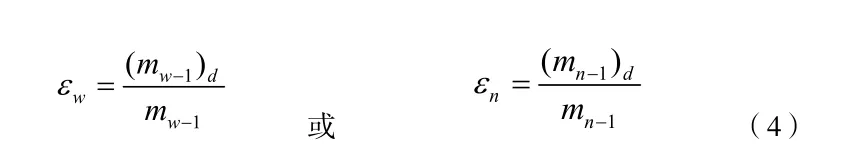
εw、εn分别称为弯曲、扭转尺寸系数。两种理论的尺寸系数相同,

3.3 构件表面质量的影响[5]
两种理论下的表面质量系数β相等,

综合上述,对应循环下构件的持久极限为

而应力理论下的构件在对称循环下持久极限为

式(8)将被式(7)所取代。
4 对称循环下构件疲劳强度的计算
构件的强度条件为

式(9)将代替以下应力理论公式

把强度条件用安全系数形式表达为

式中,n为规定的安全系数,nm为工作安全系数。
把式(7)代入式(11),可得弯曲、扭转交变应矩的强度条件为

公式(12)将取代以下应力理论的强度条件公式



图3 对称循环的疲劳计算实例
(1)用应力理论解。
① 计算轴在A-A截面上的最大工作应力。
若不计键槽对抗弯截面系数的影响,则其抗弯截面系数为

轴在不变弯矩M作用下旋转,故为弯曲变形下的对称循环,则


确定A-A轴面上的系数kσ、εσ、β。端铣加工键槽,当σb=520MPa 时,kσ=1.65,εσ=0.84,β=0.936 。将以上数据代入式(13),求得截面A-A的工作安全系数为

轴的截面A-A处满足强度条件。
(2)用应矩理论解。
抗弯截面系数

最大弯应矩

最小弯应矩m

为等幅对称循环。
由公式(b),碳素钢弯应矩为

截面A-A处不满足强度要求。

解(1)用应力理论解。

为等幅对称循环。
查表(对应的曲线图及表格见《材料力学》“交变应力”一章)可得,当

即应力理论下,该循环满足强度要求。
(2)用应矩理论解。

为等幅对称循环。

则应矩持久极限可见在应矩理论下,该循环不满足强度要求。
对比[例1]和[例2]可知,轴径越大,应矩理论下的疲劳安全系数越小。本文用非零应矩弹性理论,对等幅非对称循环交变应力下的构件的疲劳强度计算和弯曲与扭转组合等幅交变应力下构件的强度计算都进行了修正。篇幅所限,这里略。
[1]韩文坝.黄双华.非零应矩弹性理论[M].重庆:重庆大学出版社,2013.
[2] 钱伟长.叶开沅.弹性力学[M].北京:科学出版社,1956.
[3]范钦珊.殷雅俊.材料力学[M].北京:清华大学出版社,2005.
[4](美)J.M盖尔(James M.Gere) Mechanics of Materials[M].北京:机械工业出版社,2002.
[5][美]Pobertl.Mott.Applied Strength of Materials.重庆:重庆大学出版社,2005.
G322
B
1007-6344(2016)04-0347-03
[念红芬(1974.02),女,云南陆良人,硕士研究生,讲师,攀枝花学院教师,主要从事土木工程教学科研设计工作。

